基于Morlet小波技术的北京平原地面沉降周期性分析

王 洁,宫辉力,陈蓓蓓,高明亮, 周超凡,梁 悦,陈文锋

1.三维信息获取与应用教育部重点实验室，北京 100048 2.城市环境过程与数字模拟国家重点实验室培育基地，北京 100048 3.首都师范大学资源环境与旅游学院，北京 100048

0 引言

地面沉降是在自然和人为双重因素的影响下，由于地壳表层土体的压缩而导致区域性地面标高缓慢降低的一种不可补偿的永久性环境地质灾害。地面沉降具有生成缓慢、持续时间长、影响范围广、成因机制复杂和防治难度大等特点[1]。从20世纪60年代以来，北京平原区地面沉降一直呈快速发展的趋势。早在2003年，北京平原出现了昌平沙河—八仙庄、顺义平各庄、东北郊—来广营、东郊八里庄—大郊亭和大兴榆垡—礼贤五大沉降区，形成了近1 000 km2的地下水位降落漏斗。研究[2]表明，北京市地面沉降的主要原因是长期的地下水过量开采。近年来，随着南水北调工程以及地下水限制开采政策的实施，北京市地下水开采量有所减缓。但据统计，目前北京市50%～60%的供水仍来自地下水，由此引发的地面沉降仍未得到有效控制。因此，通过地面沉降监测及其周期性分析，掌握地面沉降演化规律，对制定控制地面沉降、限制地下水开采措施有重要的支撑作用。

传统的地表形变沉降监测手段主要包括水准测量和GPS。然而水准测量方法耗时长，监测范围有限；GPS测量设备造价昂贵，定期维护费用高，监测密度小。相比之下，合成孔径雷达干涉(InSAR)技术可以获取大范围、高精度的地表形变信息[3]。为了克服时间基线过长造成的失相干，Ferretti等[4]在1999年提出了永久散射体干涉测量(persistent scatterer Interferometry , PSI)技术。PSI技术选择高相干点的永久散射体，极大地提高了长时间序列干涉测量的精度和可靠性。干涉点目标分析(IPTA)方法由Charles Werner[5]于2003年提出。其核心思想是：对具有稳定频谱特性的点目标相位信息进行时间维和空间维的复合分析，得到其时序形变信息。IPTA技术同样可以克服时间基线过长引起的失相干，同时提高数据处理效率[6-8]。

目前，国内外学者针对地面沉降的演化特征、成因机理等方面有许多讨论和研究。在演化特征方面，研究者[9-10]结合水文地质条件、土地利用类型差异等研究地面沉降的演化规律。葛大庆等[11]利用InSAR长时间序列研究德州市地面沉降-回弹与地下水波动特征，结果表明地面沉降与地下水位变化密切相关。雷坤超等[12]基于PS-InSAR技术建立地面沉降综合分析模型，揭示了北京区域地面沉降的不均匀性，发现北京的多个沉降漏斗连成一片，沉降受雨水渗入补给影响较大，有季节波动性特征。成因机理方面的研究[13-14]表明，长期超量开采地下水和天然气等资源是目前平原区地面沉降的主要诱发原因。例如，贾三满等[2]认为北京平原区地面沉降主要是由于超量抽汲地下水引起。Estelle Chaussard等[15]发现，地下水及天然气的开采是造成印度尼西亚地面沉降的主要原因。陈蓓蓓等[16]采用InSAR技术、多源遥感技术与水文地质学交叉研究，揭示了北京平原区地下水演化与地面沉降响应机理；还发现北京平原区地面沉降与建筑载荷密度存在一定的相关关系。付延玲等[17]研究发现由高层建筑荷载引起的地面沉降是以建筑物中心为漏斗中心的漏斗状。周超凡等[18]采用数据场模型发现了北京市地面沉降较为严重的朝阳区北部与中部区域有高交通载荷。

小波分析是一种信号时、频局部化分析的新方法，在信号处理、图像压缩等领域有广泛的应用[19]。其原理是通过将时间序列分解到时间频率域内，可以得到时间序列的显著波动模式，即周期变化动态。Morlet小波变换能有效地分离出隐藏在时间序列中的多种变化周期。早在2010年，研究者[20-22]将小波分析引入地面沉降研究，拓宽了其应用范围。最先将小波分析引入地理学的是Grinsted等[23]，其使用交叉小波变换(XWT)和小波相干性(WTC)研究北极涛动与海冰范围特征。在国内，朱锋等[24]将小波方法应用到了地面沉降研究中，用bd5小波识别京津冀高铁北京段的不均匀沉降段；高明亮等[25]针对北京国际机场地面沉降问题，采用了连续小波变换(CWT)分析地面沉降与地下水的关系。

本文选取27景Radarsat-2数据，采用IPTA方法获取北京平原区域地面沉降监测信息，结合Morlet小波分析方法，分析了监测井的地面沉降周期性演化特征。

1 研究区概况

研究区位于北京市朝阳区东部、顺义区南部和通州区西部的交界区域，地理位置为116°24′00″E—116°45′00″E， 39°48′00″N—40°07′00″N，面积为731.50 km2(图1)。北京市由西北向东南、从山前至平原，第四系沉积厚度逐渐增大、层次增多，沉积物颗粒变细。研究区第四系黏性土可压缩层厚度为60～250 m[26]。自1987年至今，北京市地下水持续超量开采，使北京平原区的地下水位逐年下降，导致土层压缩，从而引发了地面沉降。目前，区域内包括东郊八里庄—大郊亭、东北郊—来广营2个地面沉降区；且地面沉降呈逐年加剧，沉降漏斗连成一片的趋势。本文在研究区中任意选择4个监测井，分别为1#、2#、3#、4# (图1)，将距离各监测井200 m内永久散射体(persistent scatterer，PS点)沉降均值作为该点沉降值，研究其时间序列周期性沉降特征。

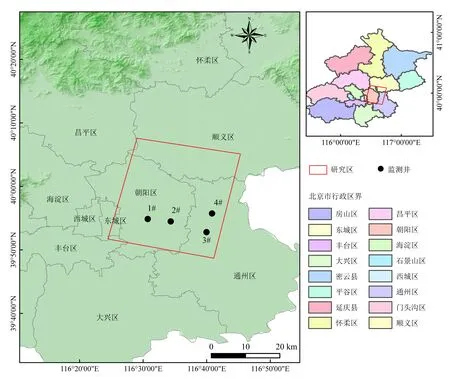
图1 研究区位置Fig.1 Location of the study area

2 研究方法

2.1 基于IPTA的监测方法

IPTA方法是Charles Werner[5]于2003年提出的，其利用迭代回归分析来获取形变历史、高程改正值、大气效应值等，具体步骤包括：

1)PS点的提取。选择主影像，配准合成孔径雷达(synthetic aperture radar，SAR)影像集，裁剪研究区，根据光谱属性或者稳定的后向散射强度选择PS候选点。

2)生成初始差分干涉图。根据主影像生成点差分干涉图；对于每一个干涉像对，用外部数字高程模型(digital elevation model，DEM)模拟研究区PS点高程相位，并从干涉相位中减去模拟的高程相位，得到差分干涉相位φdif。

3)对PS点差分干涉相位进行回归分析获取线性形变信息。在IPTA的相位模型中，φdif被分解为地形误差相位φtopoerr、形变相位φdef、大气效应相位φatm和噪声相位φnoise，即

φdif=φtopoerr+φdef+φatm+φnoise。

(1)

回归分析过程中将得到线性形变速率、高程改正值、残余相位。其中形变相位φdef分为线性和非线性2个部分，非线性形变暂时归入残余相位。

4)非线性形变提取。回归分析得到的残余相位包括大气效应相位、非线性形变相位、基线误差和噪声相位等；之后，根据不同相位成分在时间和空间上表现出的相关性差异，分别进行时间域和空间域的滤波处理，从而分离大气相位和噪声，得到非线性形变相位。

5)提取形变信息。将上一步骤中得到非线性形变融合到线性形变速率中，并重新计算相干点形变速率。通过对各时段沉降速率在时间上进行积分处理，获得对应每个时间点的累积形变量。

考虑到研究区和现有数据覆盖情况，本次研究选择的是2011—2014年的27景RadarSat-2数据。RadarSat-2是加拿大太空署与加拿大麦克唐纳·迪特维利联合公司(MacDonald Dettwiler and Associates Ltd.，MDA)合作的商用雷达数据。本研究所用到的数据产品，其距离向分辨率为11.8 m，方位向分辨率为5.2 m，波长为5.6 cm(为C波段数据)，重访周期为24 d。用于去除地形相位和地理编码的外部数据为美国航天飞机测图任务(SRTM3)获取的90 m分辨率的DEM。

2.2 Morlet小波分析方法

20世纪80年代初，由Morlet提出的一种具有时-频多分辨功能的小波分析(wavelet analysis)为更好地研究时间序列问题提供了可能。它能清晰地揭示出隐藏在时间序列中的多种变化周期，反映系统在不同时间尺度中的变化趋势，并能对系统未来发展趋势进行定性估计[19]。本次研究采用Morlet小波为基小波，运用连续小波变换分析北京平原地面沉降周期性特征。

对于f(t)∈L2(R)，连续小波变换(CWT)被定义为信号f(t)与小波基函数的内积:

(2)

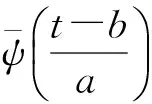
将由小波变化方程计算得到的小波系数的平方值在时间域上积分，其结果即为小波方差：

(3)

小波方差随尺度a的变化过程，称为小波方差图。由式(3)可知，它能反映信号波动的能量随尺度a的分布。因此，小波方差图可用来确定信号中不同尺度扰动的相对强度及其对应的时间尺度，即主周期。

小波变换的数据要满足正态分布，运用K-S检验可知，1#、2#、3#、4#正态分布检验结果分别为0.996、0.402、0.966和0.992。其P值(K-S检验的显著性差异)均大于0.05，通过K-S检验(置信度设为95%)，沉降值时间序列符合正态分布，可以进行小波变换。

3 结果与分析

3.1 IPTA结果及精度验证

利用IPTA获取地表形变信息，在研究区范围内，共识别191 706个PS候选点。在2011—2014年3年间，研究区各PS点年均沉降速率分布如图2a所示。从图2a可以看出，研究区最大沉降速率为162.70 mm/a。研究区内地面沉降分布不均，该时段内累积沉降量最大值为645.86 mm。采用反距离加权(IDW)方法对PS候选点的形变速率进行空间插值，得到研究区的地面沉降速率插值结果(图2b)，获取研究区沉降速率空间演化趋势。

采用自然间断点分类方法，将PS候选点分为7类，统计每一类的面积比例和PS点数。由表1可知：第1类地面沉降速率(0.00～ 22.79 mm/a )及第2类地面沉降速率(22.79～37.81 mm/a )占比较大，分别为为22.44%、24.40%，包含PS点数分别为52 809、42 917；第7类地面沉降速率(111.52～162.70 mm/a)所占面积比例最小，为5.08%。总之，地面沉降速率的分布不均匀性较大，即不均匀沉降演化趋势明显。

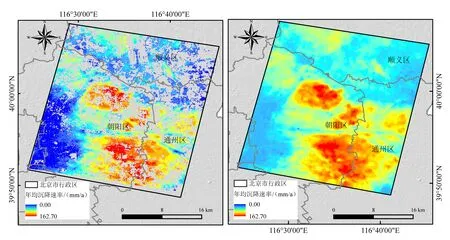
图2 研究区2011—2014年PS点沉降速率(a)及PS点沉降速率IDW插值结果 (b)Fig.2 PS subsidence rates of study area(a) and IDW interpolation results from 2011 to 2014 (b)

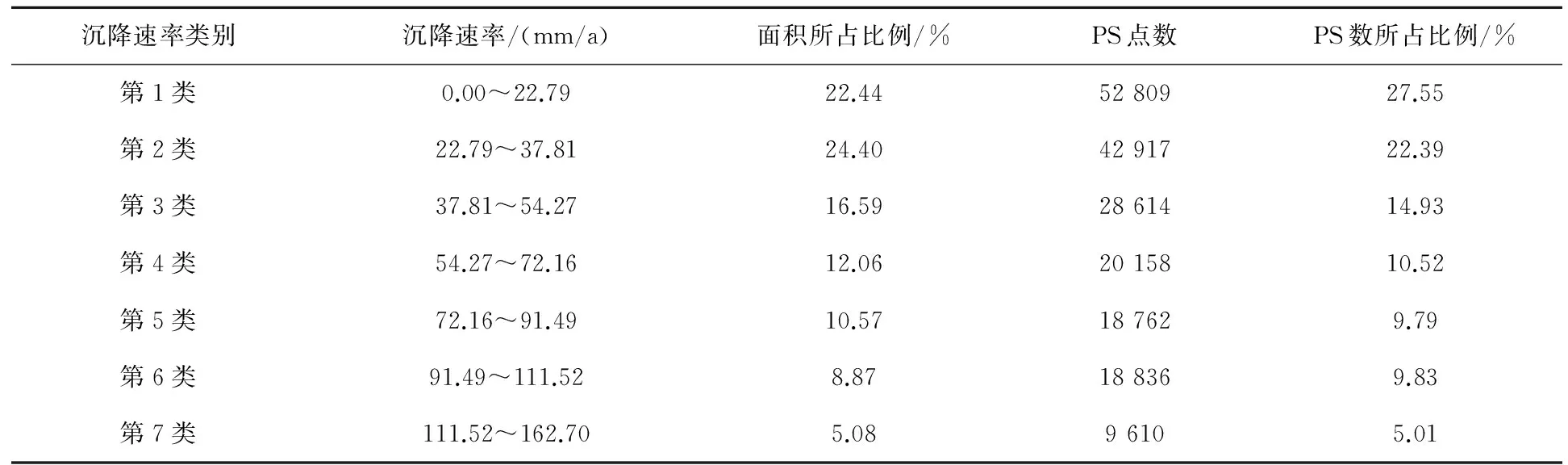
沉降速率类别沉降速率/(mm/a)面积所占比例/%PS点数PS数所占比例/%第1类0.00～22.7922.445280927.55第2类22.79～37.8124.404291722.39第3类37.81～54.2716.592861414.93第4类54.27～72.1612.062015810.52第5类72.16～91.4910.57187629.79第6类91.49～111.528.87188369.83第7类111.52～162.705.0896105.01

以水准点地理位置为参考，距离水准点200 m范围内的PS点均值作为该点形变值，计算水准观测与IPTA反演结果的误差(表2)，检验IPTA技术的监测精度。为了与IPTA获取的年均沉降速率进行比较，分别求取7个水准点在2011、2012年的年累积沉降量。校验结果显示，误差最大值为9.586 mm/a，最小值为0.906 mm/a，形变误差在1 cm/a内。在置信度为95%的条件下，相关系数达到了0.972 8，说明IPTA反演结果与水准观测结果一致。

3.2 基于Morlet小波分析典型区地面沉降周期性

小波分析要求输入的信号必须是等时间间隔的。因此，必须对现有的IPTA时间序列沉降结果进行时间域的插值。首先以4个监测井为圆心，做距离为200 m的缓冲区，缓冲区内PS点沉降均值作为该点沉降值；之后对地面沉降时间序列进行3次样条插值和误差计算，最终得到2011年6月26日到2014年11月1日期间，每隔24 d间隔的地面沉降时间序列。

将等时间间隔的沉降时间序列信号输入Morlet小波变换工具进行处理，得到小波系数，同时计算小波系数的实部、模、模方、方差，之后将小波系数方差绘制成图(图3)。如前文所述，小波系数方差图可以清楚地展示出信号中不同尺度扰动的相对强度及其对应的时间尺度，即主周期。图3a中，1#点小波方差图呈现出3个峰值，时间尺度分别对应为28、16、7 T(1 T表示1个24 d的时间段)。其中：28 T的时间尺度对应的峰值最大，说明28 T时间尺度处周期震荡最强，为该位置沉降的第一主周期；16 T时间尺度峰值次之，为1#点地面沉降时间序列的第二主周期；7 T时间尺度对应最小峰值，为该点地面沉降时序演化的第三主周期。上述3个周期的波动控制着该区域地面沉降在整个时间域内的变化特征。相似地，如图3b所示，2#点存在4个峰值，时间尺度分别为28、22、13、7 T。其中22 T对应该位置的第一主周期；28、13和7 T处分别对应其第二、第三和第四主周期，4个周期的波动控制着该区域地面沉降在整个时间域内的变化特征。图3c中，3#位置在28 T处存在1个明显峰值，其为该点地面沉降时间序列的主周期。图3d中：4#位置在28 T处存在峰值，其为对应该点地面沉降时间序列主周期；7 T为第二主周期，2个周期的波动控制着该区域地面沉降在整个时间域内的变化特征。

根据小波方差结果，分别绘制1#、2#、3#、4#位置地面沉降演化的各时间尺度 Morlet 小波变换实部过程线(图4—7)。

如图4所示，1#在28 T的时间尺度上，地面沉降演化经过了约3个整周期，平均周期为13.3月；在16 T的时间尺度上，平均周期为7.6月；在7 T的时间尺度上平均周期为3.8月。类似地，如图5所示：2#点在22 T的时间尺度上，地面沉降演化经过了约3.75个周期，平均周期为10.7月；在28 T的时间尺度上，平均周期为13.3月；在13 T的时间尺度上平均周期为6.7月；在7 T的时间尺度上平均周期为3.5月。如图6所示，3#点在28 T的时间尺度上经过了约3个周期，平均周期为13.3月。如图7所示：4#位置在28 T的时间尺度上，地面沉降演化经过了约3个周期，平均周期为13.3月；在7 T的时间尺度上平均周期为3.8月。

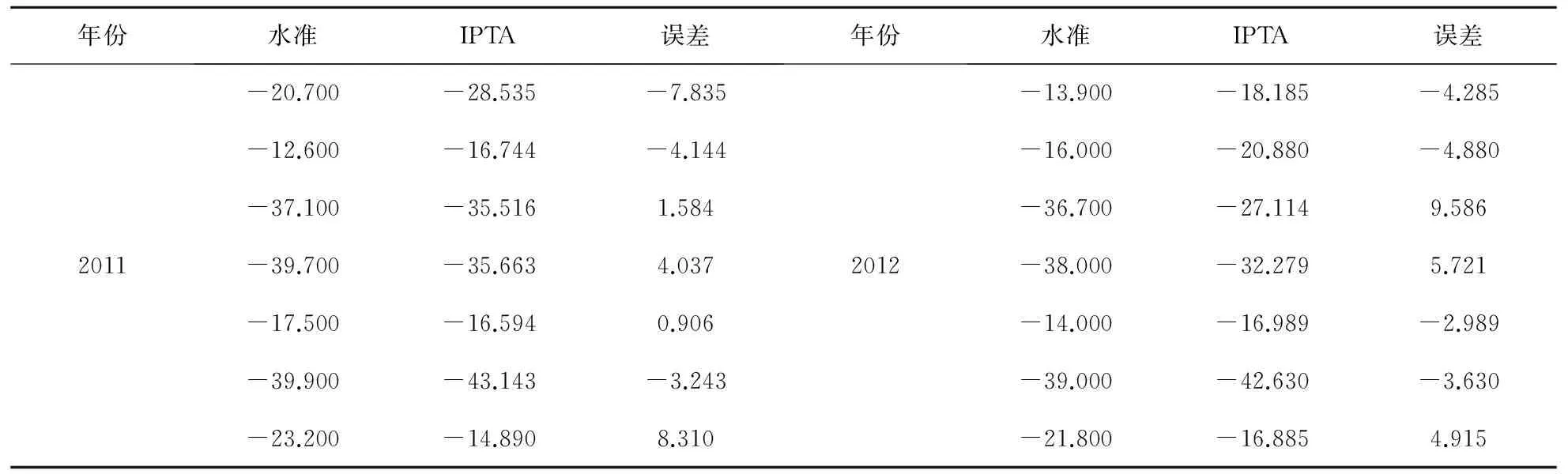
表2 2011和2012年水准监测形变量与IPTA监测年累积沉降量比较

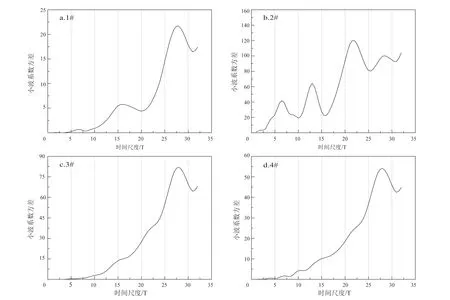
图3 小波系数方差图Fig.3 Curves of wavelet variance

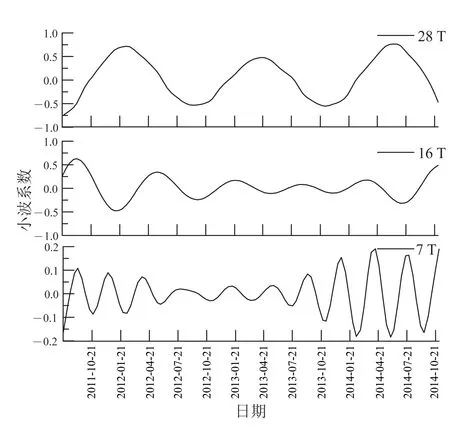
小波系数为正相位，对应尺度相应时间地面沉降量相对较大；小波系数为负相位，则地面沉降量较小。拐点(波峰和波谷)即为对应尺度下地面沉降时间序列的突变点。图4 1# 各时间尺度 Morlet 小波变换实部过程线Fig.4 Real part transform process based on Morlet wavelet in different time scales of 1#

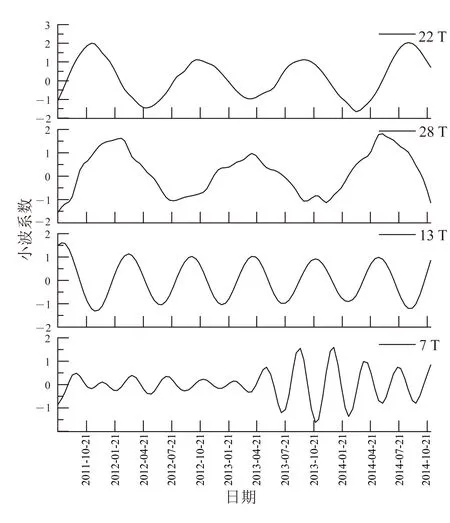
图5 2#各时间尺度 Morlet 小波变换实部过程线Fig.5 Real part transform process based on Morlet wavelet in different time scales of 2#

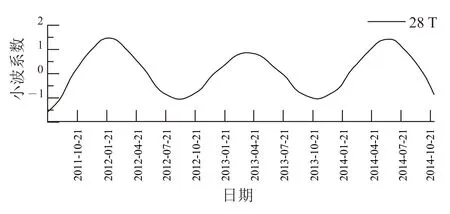
图6 3#各时间尺度 Morlet 小波变换实部过程线Fig.6 Real part transform process based on Morlet wavelet in different time scales of 3#

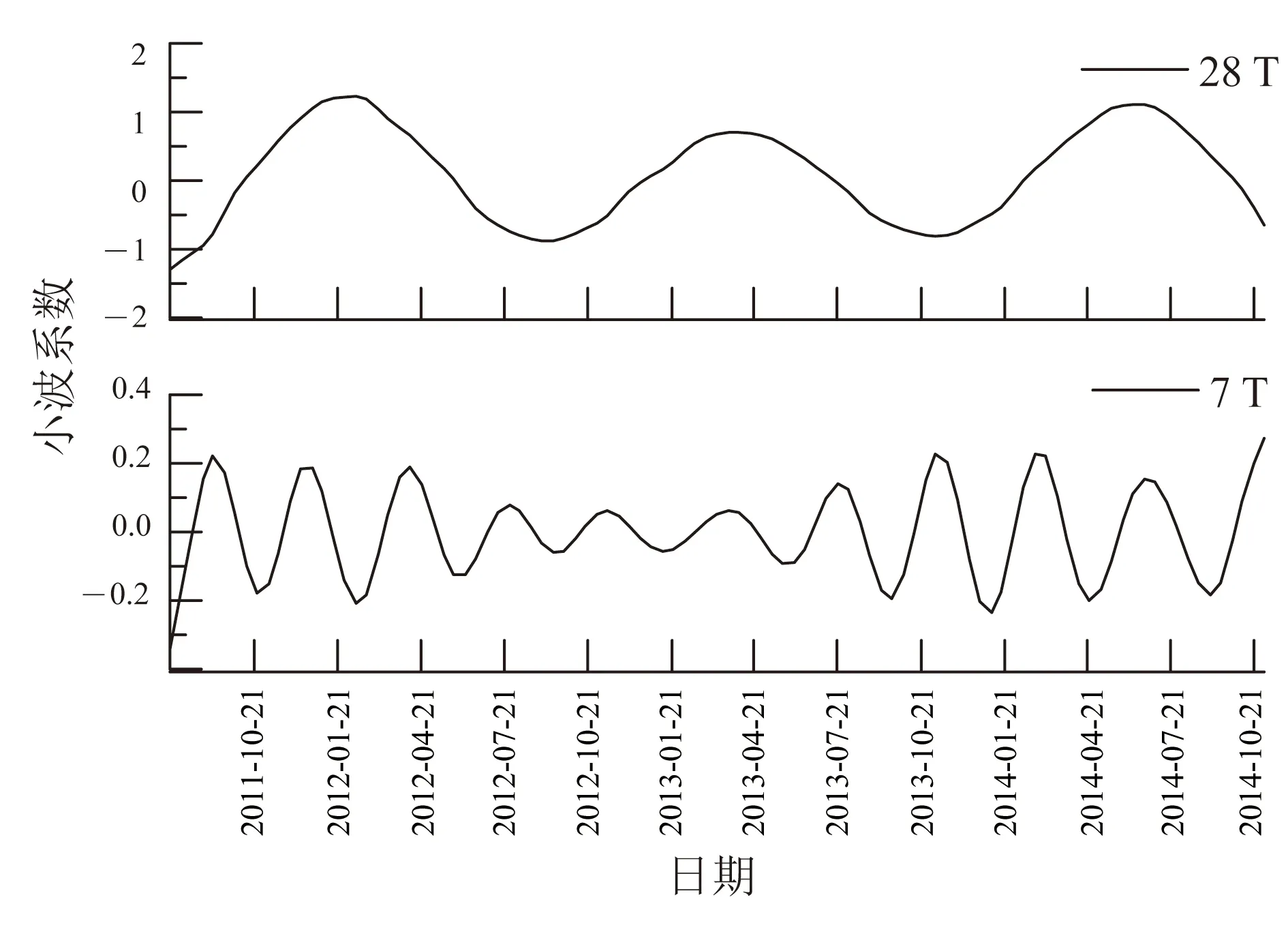
图7 4#各时间尺度 Morlet 小波变换实部过程线Fig.7 Real part transform process based on Morlet wavelet in different time scales of 4#

4 结论与建议

1)2011—2014年，北京地区地面沉降发展迅速，研究区最大年沉降速率达到162.70 mm/a，最大累积沉降量为645.86 mm。

2)以研究区内1#—4#为对象，通过Morlet小波变换分析不同时间尺度下地面沉降的周期性特征。结果表明，地面沉降时序演化在空间分布上呈现差异性特征。地面沉降周期随着研究尺度的不同而发生相应的变化，这种变化一般表现为小时间尺度的变化周期往往嵌套在大尺度的变化周期之中。地面沉降在时间域中存在多层次的时间尺度结构和局部变化特征。

3)长期超量开采地下水是北京地面沉降的主要原因。作为地下水的主要补给源，降雨量的年际变化可能影响地下水位的变化，从而也可能诱发地面沉降的季节性波动。这次研究揭示了区域地面沉降多尺度时序演化特征，在未来的研究中，需要进一步研究地面沉降与地下水时序演化的关联分析。

(

)：

[1] 郑铣鑫,武强,侯艳声,等. 关于城市地面沉降研究的几个前沿问题[J].地球学报, 2002, 23(3): 279-282.

Zheng Xixin, Wu Qiang, Hou Yansheng, et al. Some Frontier Problems on Land Subsidence Research[J]. Acta Geoscientica Sinica, 2002, 23(3):279-282.

[2] 贾三满,王海刚,赵守生,等. 北京地面沉降机理研究初探[J].城市地质, 2007,2(1)：20-26.

Jia Sanman, Wang Haigang, Zhao Shousheng, et al. A Tentative Study of the Mechanism of Land Subsidence in Beijing[J]. City Geology, 2007,2(1)：20-26.

[3] Galloway D L, Hudnut K W, Ingebritsen S E, et al. Detection of Aquifer System Compaction and Land Subsidence Using Interferometric Synthetic Aperture Radar, Antelope Valley, Mojave Desert, California[J]. Water Resources Research, 1998, 34(10):2573-2585.

[4]Ferretti A, Prati C, Rocca F. NonlinearSubsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000,38(5): 2201-2212.

[5] Werner C, Wegmuller U, Wiesmann A, et al. Inter-ferometric Point Target Analysis with JERS-1 L-Band SAR Data[C]// Geoscience and Remote Sensing Symposium. IGARSS’03 Proceedings. Toulouse:IEEE, 2003:4359-4361.

[6] 俞晓莹,姜成岭,张建,等. IPTA监测圣佩德罗湾港口地表时序沉降[J].测绘科学, 2012, 37(6):21-25.

Yu Xiaoying, Jiang Chengling, Zhang Jian, et al. IPTA Monitoring Long-Term Series Surface Deformation of SAN PEDRO[J]. Science of Surveying & Mapping, 2012, 37(6):21-25.

[7] Zhang Yonghong, Zhang Jixian, Wu Hongan, et al. Monitoring of Urban Subsidence with SAR Interferometric Point Target Analysis: A Case Study in Suzhou, China[J]. International Journal of Applied Earth Observation & Geoinformation, 2011, 13(5):812-818.

[8] 张海波,李宗春,许兵,等. IPTA方法在地面沉降监测中的应用[J].测绘科学技术学报,2016, 33(2):145-149.

Zhang Haibo, Li Zongchun, Xu Bing, et al. Ground Subsidence Monitoring Using Interferometric Point Target Analysis[J]. Journal of Geomatics Science and Technology, 2016, 33(2):145-149.

[9] 张雯,宫辉力,陈蓓蓓,等. 北京典型区地面沉降演化特征与成因分析[J].地球信息科学学报, 2015, 17(8):909-916.

Zhang Wen, Gong Huili, Chen Beibei, et al. Evolution and Genetic Analysis of Land Subsidence in Beijing Typical Area[J]. Journal of Geo-Information Science, 2015, 17(8):909-916.

[10] 杨艳,贾三满,王海刚.北京平原区地面沉降现状及发展趋势分析[J].上海地质,2010(4):23-28.

Yang Yan, Jia Sanman, Wang Haigang. The Status and Development of Land Subsidence in Beijing Plain[J]. Shanghai Geology, 2010 (4):23-28.

[11] 葛大庆,殷跃平,王艳,等. 地面沉降-回弹及地下水位波动的InSAR长时间序列监测:以德州市为例[J].国土资源遥感，2014,26(1):103-109.

Ge Daqing, Yin Yueping, Wang Yan, et al. Seasonal Subsidence-Rebound and Ground Water Level Changes Monitoring by Using Coherent Target Insar Technique: A Case Study of Dezhou,Shandong[J]. Remote Sensing for Land & Resources, 2014, 26(1):103-109.

[12] 雷坤超,陈蓓蓓,贾三满,等. 基于PS-InSAR技术的北京地面沉降特征及成因初探[J]. 光谱学与光谱分析, 2014,34(8):2185-2189.

Lei Kunchao, Chen Beibei, Jia Sanman, et al. Primary Investigation of Formation and Genetic Mechanism of Land Subsidence Based on PS-InSAR Technology in Beijing[J]. Spectroscopy and Spectral Analysis, 2014, 34(8):2185-2189.

[13]Chai Jinchun, Shen Shuilong, Zhu Hehua, et al. Land Subsidence Due to Droundwater Drawdown in Shanghai[J]. Géotechnique, 2004, 54(2):143-147.

[14] Amelung F, Galloway D L, Bell J W, et al. Sensing the Ups and Downs of Las Vegas: InSAR Reveals Structural Control of Land Subsidence and Aquifer-System Deformation[J]. Geology, 1999, 27(6):483-486.

[15] Chaussard E, Amelung F, Abidin H, et al.Sinking Cities in Indonesia: ALOS PALSAR Detects Rapid Subsidence due to Groundwater and Gas Extraction[J].Remote Sensing of Environment,2013, 128(1):150-161.

[16] 陈蓓蓓,宫辉力,李小娟,等. PS-InSAR技术与多光谱遥感建筑指数的载荷密度对地面沉降影响的研究[J]. 光谱学与光谱分析, 2013, 33(8):2198-2202.

Chen Beibei, Gong Huili, Li Xiaojuan, et al. The Impact of Load Density Differences on Land Subsidence Based on Build -Up Index and PS -InSAR Technology[J]. Spectroscopy and Spectral Analysis, 2013, 33(8):2198-2202.

[17] 付延玲, 骆祖江, 廖翔,等. 高层建筑引发地面沉降模拟预测三维流固全耦合模型[J]. 吉林大学学报(地球科学版), 2016,46(6): 1781-1789.

Fu Yanling, Luo Zujiang, Liao Xiang, et al. A Three-Dimensional Full Coupling Model to Simulate and Predict Land Subsidence Caused by High-Rise Building. Journal of Jilin University(Earth Science Edition), 2016, 46(6): 1781-1789.

[18] 周超凡, 宫辉力, 陈蓓蓓,等. 利用数据场模型评价北京地面沉降交通载荷程度[J]. 吉林大学学报(地球科学版), 2017,47(5): 1511-1520.

Zhou Chaofan, Gong Huili, Chen Beibei, et al. Assessment to Ground Subsidence Traffic Load in Beijing Area Using Data Field Mode[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(5): 1511-1520.

[19] 王文圣,丁晶,向红莲.水文时间序列多时间尺度分析的小波变换法[J].四川大学学报(工程科学版),2002, 34(6):14-17.

Wang Wensheng, Ding Jing, Xiang Honglian. Multiple Time Scales Analysis of Hydrological Time Series With Wavelet Transform[J]. Journal of Sichuan University(Engineering Science Edition), 2002, 34(6):14-17.

[20] 王文圣,丁晶,向红莲. 小波分析在水文学中的应用研究及展望[J]. 水科学进展, 2002,13(4): 515-520.

Wang Wensheng, Ding Jing, Xiang Honglian. Application and Prospect of Wavelet Analysis in Hydrology[J]. Advances in Water Science, 2002,13(4): 515-520.

[21] 郭琳,宫辉力,朱锋,等. 基于小波分析的地下水水位与降水的周期性特征研究[J].地理与地理信息科学,2014,30(2):35-38.

Guo Lin, Gong Huili, Zhu Feng, et al. Cyclical Characteristics of Groundwater Level and Precipitation Based on Wavelet Analysis[J]. Geography and Geo-Information Science, 2014,30(2):35-38.

[22] 倪夏梅,陈元芳,刘勇,等. 基于小波分析的枯水径流多时间尺度分析[J].水电能源科学, 2010, 28(3):6-8.

Ni Xiamei, Chen Yuanfang, Liu Yong, et al. Multiple Time Scale Analysis of the Low Water Runoff Based on Wavelet Analysis[J]. Water Resources & Power, 2010, 28(3):6-8.

[23] Grinsted A, Moore J C, Jevrejeva S. Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series[J]. Nonlinear Processes in Geophysics, 2004, 11(5/6):561-566.

[24] 朱锋,宫辉力,李小娟,等. 基于InSAR和小波变换的不均匀沉降段识别:以京津高铁北京段为例[J].地理与地理信息科学, 2014, 30(1):23-27.

Zhu Feng, Gong Huili, Li Xiaojuan, et al. Identification of Uneven Land Subsidence Segment Based on the InSAR and Wavelet Transformation: A Case Study of Beijing Section of Beijing-Tianjin High-Speed Railway[J]. Geography and Geo-Information Science, 2014, 30(1):23-27.

[25] Gao Mingliang, Gong Huili, Chen Beibei, et al. In SAR Time-Series Investigation of Long-Term Ground Displacement at Beijing Capital International Airport, China[J]. Tectonophysics, 2016, 691:271-281.

[26] 姜媛, 杨艳, 王海刚,等. 北京平原区地面沉降的控制与影响因素[J].上海国土资源, 2014,35(4):130-133.

Jiang yuan, Yang Yan, Wang Haigang, et al. Factors Controlling Land Subsidence on the Beijing Plain[J]. Shanghai Land & Resources,2014,35(4):130-133.