基于Chebyshev走时逼近的三维多次反射射线计算
2018-05-26孙建国
孙建国,苗 贺
吉林大学地球探测科学与技术学院,长春 130026
0 引言
射线走时和射线路径是构成零阶几何射线场(亦称为几何光学场)的两个基本要素。其中,射线走时对应高频波场的相位,射线路径对应高频波场的能量传播轨迹。因此,自从射线理论被引入到地震学中以来,对射线走时和射线路径计算方法的研究就一直没有间断过,尤其是在20世纪80年代以后,在反射地震偏移和反演研究的推动下[1-2],对射线走时和射线路径的研究一度成为研究热点,有很多研究者和工程师参与到其中,提出了很多方法和技术[3-9]。形成这种局面的主要原因是基于射线理论的偏移和反演方法具有对输入数据体观测装置适应性强和计算速度快等优点[1-2]。再有,在偏移成像中的射线追踪与常规的两点射线追踪有所不同,只须设定射线起点的位置,而不须设定射线终点的位置。这是因为基于射线理论的偏移在具体实施上是个一点对多点过程,任意一个成像点上的射线走时和射线方向均可利用相邻点上的相关信息通过插值得到。然而,由于这种只考虑初值的射线追踪方法不能在计算过程中随时插入由非均匀介质中的聚焦和反聚焦现象所产生的新射线(散射射线),从而会在成像区域形成射线覆盖盲区。因此,在20世纪90年代以后,无论是工业界还是学术界均倾向于采用波前构建法来替代常规的初值射线追踪法,并逐步建立了基于波前构建的Kirchhoff型偏移和波束偏移[1-2]。但是,波前构建法在实现时需要利用复杂的数据结构,而且对于多路径走时的存储也比较复杂[10-14]。所以,在20世纪90年代以后,基于程函方程数值分析的射线走时计算方法逐步受到关注和重视[1-5]。
在历史上,利用程函方程数值解计算地震波走时的基本思想早已有之,但是由于没有相应的需求而一直不为人所关注。1988年,Vidale首先将前人的基本思想付诸实践[3-4],提出了基于程函方程有限差分(FD)数值解的地震波走时计算方法。与上文提到的初值方法相比,FD法具有计算速度快和没有计算盲区等特点,从而可以作为一种理想的地震波走时计算方法替代传统的射线追踪法。然而,在无人为干预时,利用有限差分等基于网格的程函方程数值分析方法只能沿着波的前进方向计算走时,而不能沿着波的回折方向计算走时。换句话说,在无人为干预时,利用任何一种基于程函方程数值分析的方法均只能计算沿着波的前进方向的透射(波)走时,而不能同时计算由该透射波所激发的反射(波)走时,更不能计算由该透射波所激发的、其传播方向经过多次改变的多次透射(波)和多次反射(波)走时。针对这个问题,Rawlinson等[5]在2004年提出了一种在人为干预下利用程函方程数值分析方法计算多次透射和多次反射走时的分区多级方案,在这种方案中,走时计算采用了基于窄带技术的快速推进法(fast marching method,FMM)[5]。为计算多次反射走时,Rawlinson等[5]将每一个带有光滑弯曲界面的非均匀层视为一个独立的计算单元,而每一个层面均被视为窄带(层面窄带)。在层面窄带中,快速推进过程被反复重置为初始状态(重新初始化),并根据预定的传播方向重新进行推进计算。为了计算射线路径,Rawlinson等[5]采用了逆向梯度法,即首先利用有限差分网格节点上的走时值计算走时梯度,然后再根据梯度方向计算射线路径的局部坐标,最后将所有的局部坐标点连成一体,得到射线路径。
2006年,de Kool等[6]将上述计算方法推广到三维。2017年,孙章庆等[7]将这种多级计算方法与群推进法组合在一起,提出了一种针对复杂山地多波型走时计算的多级次群推进迎风混合法。类似地,唐小平等[8]将多级计算方法与最短路径算法组合在一起,提出了一种基于最短路径法的、针对三维层状介质中多次波的走时与射线路径计算方法。在理论上,分区多级计算的基本思想可以用于任何一种基于程函方程数值分析的地震波走时计算方法,因此存在有无限多的组合方式。
无论是在Rawlinson等的开创性工作中,还是在后续的跟踪完善性工作中,走时梯度都是直接利用网格点走时值来计算的。由此而产生的问题是:①梯度计算的精度和稳定性受有限差分网格常数的制约,并且随计算区域和网格密度的变化而变化,尤其是在复杂(曲)边界附近或是在变网格中更是如此;②梯度计算的精度和稳定性受单个网格点走时精度的制约。为解决这个问题,张东等[15]采用B样条插值多项式,将对离散数据的数值求导问题转化为对分片光滑函数的求导问题。2014年,张婷婷等[16]将B样条插值用于三维层状介质中的多次波走时和多次波射线路径计算,为在三维条件下研究多次反射提供了一个新的计算途径。然而,根据张婷婷等[17]的计算结果,基于B样条插值多项式的计算方法会在速度突变区域内产生一定的误差,因而难以在速度剧烈变化区域内得到满意的计算结果。本文针对这个问题:①利用Chebyshev正交多项式逼近走时场,使分区多级计算的误差在最小二乘的意义下达到最小,从而避开速度突变所带来的走时突变问题;②对Chebyshev逼近函数求导,得到射线路径在所考虑区域内的局部坐标。
1 基于程函方程有限差分解的分区多级走时计算
根据Rawlinson等[5]的工作,分区多级计算的主要步骤是:①在模型中划分出反射区和透射区。②将反射(透射)区内的网格点划分为接收点、活动点和远离点(图1),其中:接收点位于窄带以外的上风区,是已经完成走时计算的点;活动点位于窄带之内,是当前正在进行走时计算的点;远离点位于窄带以外的下风区,是还没有进行走时计算的点。③利用公式
(1)
计算所考虑活动点上走时梯度的模。式中:Si,j,k为网格慢度;|t|i,j,k为走时梯度的模;和分别表示点(i,j,k)处走时在对应方向上的n阶向前和向后差分算子。当n=1时,
(2)
式中,h为网格间距。④将最小走时值赋予所考虑的活动点,并将其标记为接收点,移出窄带。⑤将距所考虑活动点最近的远离点移入窄带,重复③—④所描述的计算过程,直到全部远离点均变为接收点。
图2给出了上述分区多级计算步骤的进一步说明。①首先由震源开始,计算反射(透射)面及以上区域内所有网格点处的走时(图2a)。②将界面(反射(透射)面)重置为窄带(图2b)。③为计算反射波,将界面(反射(透射)面)以上的点设为远离点,按照上文中的计算步骤重启FMM(图2c)。为计算透射波,将界面(反射(透射)面)以下层内的点设为远离点,按照上文中的计算步骤重启FMM(图2d)。重复图2所描述的计算过程,即可得到任意级次的多次反射和多次透射。

图1 反射(透射)区内的接收点(黑色圆点)、活动点(灰色圆点)和远离点(白色圆点)Fig.1 receiver point (black), active point (gray) and far point (white) in reflection (transmission) region
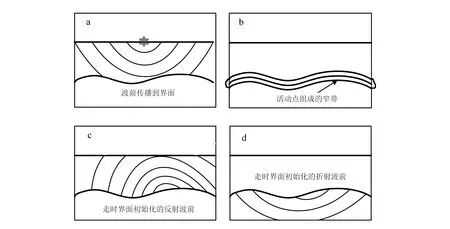
据文献[4]修改。图2 分区多级走时计算过程示意图Fig.2 Partition multi-level travel time calculation process
2 基于Chebyshev多项式的离散走时逼近
Chebyshev逼近是基于Chebshev多项式的一种逼近方法,是为解决零偏差问题而提出的一种基于正交多项式的最佳逼近方法[18]。在历史上,Chebyshev逼近和Chebshev多项式由俄罗斯数学家P L Chebyshev在1854年提出,其最初目的是解决连杆设计问题[19]。根据其数学表现形式可将Chebyshev提出的多项式分为两种,即第一类和第二类Chebyshev多项式。其中,第一类Chebyshev多项式起源于多倍角余弦和正弦函数展开,用Tn(x)表示。具体地讲,Tn(x)=cos[ncos-1(x)]。第二类Chebyshev多项式用Un(x)表示,与Tn(x)的关系为Un(x)=[dTn+1(x)/dx]/(n+1)。在实际应用中,利用下列递推公式计算Tn(x)和Un(x),即T0(x)=1、T1(x)=x、Tn+1(x)=2xTn(x)-Tn-1(x)、U0(x)=1、U1(x)=2x、Un+1(x)=2xUn(x)-Un-1(x)。
作为一种正交多项式,Chebyshev多项式与其他正交多项式相比,例如与Legendre、Laguerre和Hermite等正交多项式相比具有许多独特的性质[9]。事实上,Chebyshev多项式特别适合于进行最佳平方逼近。此外,在一定条件下可将连续函数展开为Chebyshev级数等等。因此,为在最小平方意义下逼近来自于快速推进法的走时场,在下文中选取Chebyshev多项式为逼近函数。如图3所示,在诸多正交多项式中,Chebyshev多项式的方差最小,即逼近误差亦为最小。
现在利用第一类Chebyshev多项式Tn(x)来构造3维离散走时τ(x,y,z)的近似解析表达式t(x,y,z)。为此目的,引入系数序列a′m,m=0,1,…,8,使得
(3)
展开后得到
t(x,y,z)=a0+a1z+a2(2z2-1)+a3y+
a4yz+a5y(2z2-1)+a6(2y2-1)+
a7z(2y2-1)+a8(2y2-1)(2z2-1)+
a9x+a10xz+a11x(2z2-1)+a12xy+
a13xyz+a14xy(2z2-1)+a15x(2y2-1)+
a16(2y2-1)xz+a17x(2y2-1)(2z2-1)+
a18(2x2-1)+a19(2x2-1)z+
a20(2x2-1)(2z2-1)+
a21(2x2-1)(2y2-1)+
a22(2x2-1)y+a23(2x2-1)yz+

图3 三种数据4种多项式逼近效果(a、b、c)及方差对比图(d)Fig.3 Four polynomial approximations for three kinds of data (a, b, c) and variance comparison chart (d)
a25(2x2-1)(2y2-1)z+
a26(2x2-1)(2y2-1)(2z2-1)。
(4)
式中,ap(p∈0,1,2,…,26)是利用最小二乘法得到的插值系数,即
(5)
式中:τ(xi,yj,zk)为网格节点上的走时值;φp(xi,yj,zk)(p∈0,1,2,…,26)为逼近函数中与系数对应的正交项;M,N,L分别为x,y,z方向的网格节点数。
一旦完成了公式(4)所描述的逼近过程,即可根据走时函数t(x,y,z)的梯度函数t(x,y,z)求取当前追踪点的射线方向。根据定义,
t(x,y,z)=
(6)
3 数值计算实例
3.1 常梯度速度模型
首先考虑图4中所示的常梯度速度模型。模型尺度为x×y×z=500 m×500 m×250 m,网格间距为10.0 m。震源点坐标是(1.0 m,1.0 m,1.0 m);接收点均匀地分布在模型表面上,其间距为20.0 m;速度分布函数为v=500+60z。式中:z为深度;v为速度。
对比图4a、b可见:Chebyshev逼近法所得到的射线路径在源点附近优于B样条插值法;在其他区域,两者所得射线路径在整体上相差不大。为便于进一步对比,取y=25.0 m处的xz剖面进行对比,其结果示于图5,可以看出,Chebyshev逼近法所给出的走时具有较小的相对误差。另外,在一台CPU为酷睿i5的台式机(CPU 频率为2 450 MHz;内存为6 G RAM)上计算时,B样条插值法所用的CPU时间为5.191 s,而Chebyshev逼近法所用的 CPU时间为4.205 s,其计算效率相差约20%。因此,综合来看,在这个模型中,Chebyshev逼近法要优于B样条插值法。
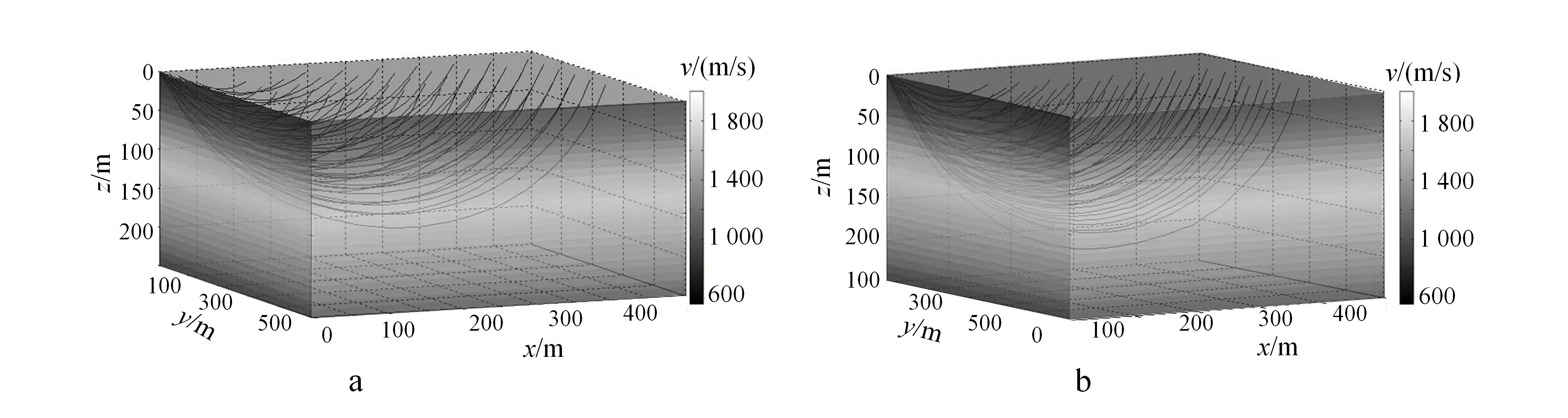
a.Chebyshev插值法;b.B样条插值法。图4 速度连续变化模型射线路径图Fig.4 Ray path diagram of continuous velocity model

a .Chebyshev插值法;b.B样条插值法;c.B样条插值(黑色)与Chebyshev多项式逼近(灰色)走时相对误差对比。图5 速度连续变化模型射线路径侧面图Fig.5 Continuous velocity model ray path side view
3.2 Marmousi模型数值计算
为检验在上文中所提出的方法在复杂模型中的计算精度,首先利用三维Marmousi模型进行对比研究。图6给出了三维Marmousi模型中一个剖面上的对比结果,不难看出:运动学射线追踪虽然能准确地计算出射线路径,但是存在射线路径盲区,从而不能求出模型内的全部走时;与此相反,在Chebyshev逼近法中,射线路径是通过走时来计算的,而且是程函方程的有限差分解,存在于整个速度模型之中,因此,在Chebyshev逼近法中没有射线覆盖盲区问题。值得指出的是,虽然利用基于程函方程有限差分法的Chebyshev逼近法能算出整个模型中的射线路径,但是考虑到过多的射线条数会影响对比效果,所以在图6中只在射线追踪法的覆盖区内进行了对比。
3.3 多次透射一次反射

黑色射线为运动学射线追踪结果;灰色射线为Chebyshev逼近法结果;白色等值线为用FMM得到的走时等值线(等时线)。图6 Marmousi模型射线路径对比Fig.6 Marmousi model ray path comparison
图7a、b分别给出4层水平层状模型中的透射走时和在第4层底边界的反射走时。图7c给出的是在第4层底边界利用Chebyshev逼近法得到的一次反射射线路径,其中透射部分的射线均垂直穿过在图7a中所给出的等时线,反射部分的射线均垂直穿过图7b中所给出的等时线。图7d是利用Chebyshev逼近法求得的所有4个层面上的入射与反射射线路径。图7e给出的是Chebyshev逼近法与样条插值法之间关于射线路径计算的相对误差对比,可以看出,Chebyshev逼近法的精度要高于B样条插值法的精度。

a.4层模型中的透射等时线;b.第四层底边界的一次反射等时线;c.第四层底边界的一次反射射线路径;d.4层模型中所有4个层面上的反射射线路径;e.根据d图计算的走时相对误差。图7 4层水平层状模型多次反射透射路径图Fig.7 Multiple reflection transmission ray path diagram of 4-level horizontal layered model
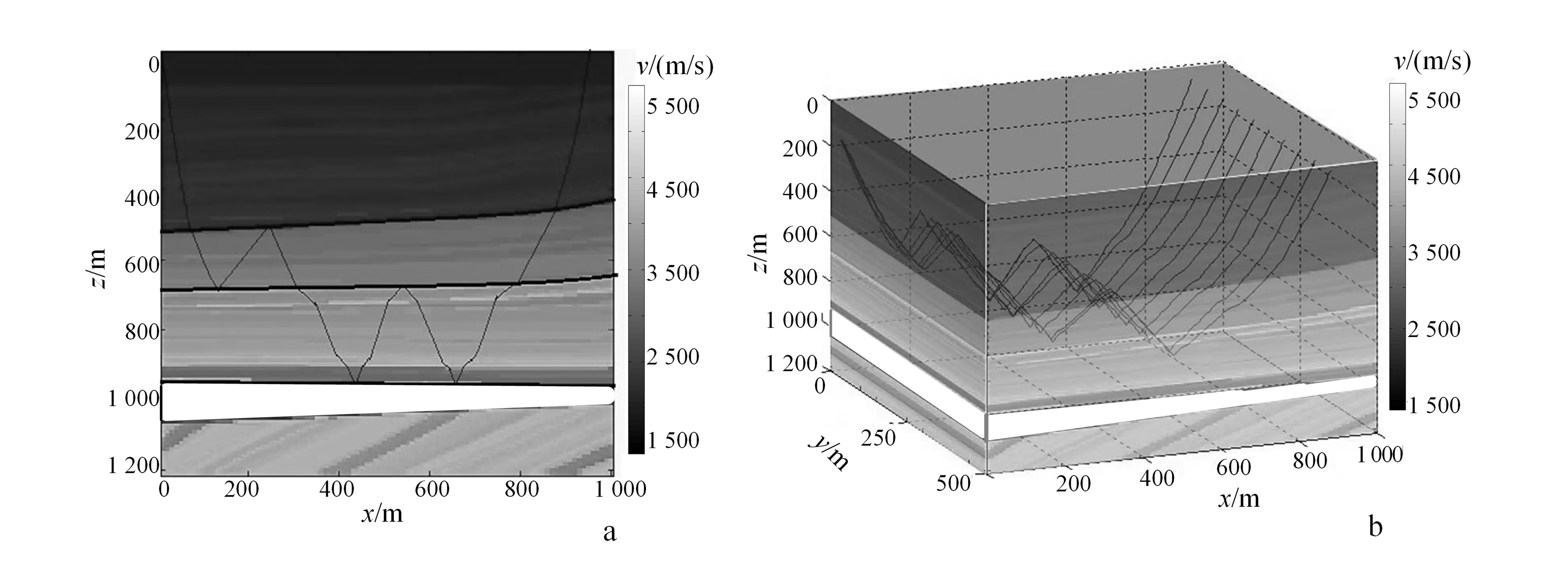
a.Marmousi模型分层与剖面路径图(据文献[8]);b.Marmousi三维路径图。图8 Marmousi模型多次反射路径图 Fig.8 Marmousi model multiple reflection ray path diagram
3.4 层间多次反射
为考察Chebyshev逼近法计算多次反射的效果,首先选取Marmousi模型中的一个小部分,构成局部层状介质(图8)。由图8可见:高速区射线路径偏向层面方向,而低速区射线偏向层面的法线方向。这与Snell定律所要求的完全一致,说明基于Chebyshev逼近的射线路径计算是正确的。
鉴于在图8所示模型中,Chebyshev逼近和B样条插值之间的误差对比分析与图7e中的结果类似,故在此不再进行专门的讨论。
其次,考察高速度反差条件下Chebyshev逼近法的计算效果。为此选用二维Sigsbee模型,其计算结果展示在图9中。为了保证能在盐丘底部形成有效的多次反射,将震源置于远离高速体的位置,并以模型的底界面为一次反射面。首先,利用多级次FMM计算出整个模型中的多次反射走时,再从模型顶界面开始进行逆向梯度计算,进而得到如图9所示的射线路径。为方便起见,只计算了模型底界面和盐丘底界面之间的2次反射射线路径。尽管如此,也可以清晰地看出在高速体存在时的层间多次反射始终满足Snell定律,且由高速体向低速区域呈“扫把”形出射。这进一步地说明了Chebyshev逼近法计算一次和多次反射射线路径的有效性。

图9 Sigsbee模型剖面Fig.9 Sigsbee model section
4 结论
针对利用B样条插值进行走时梯度计算所存在的问题(在速度突变时会出现较大的计算误差),本文提出利用Chebyshev多项式替代B样条对走时场进行逼近,并在此基础上结合多级快速推进法(FMM)建立了一种计算三维多次反射射线的方法。根据简单的水平层状介质和复杂的Marmousi和Sigsbee模型中的数值计算结果可以得到下列结论:
1)利用Chebyshev多项式逼近走时可以有效地解决离散数据求导过程中出现的不稳定问题,以及B样条插值法在速度突变时所引起的大误差问题,并能较好适应分区多级次算法得到的多次反射、透射走时场。
2)Chebyshev逼近法在简单和复杂模型中均能保证所计算出的射线路径具有较高的精度,能够满足偏移成像的要求。
(
):
[1] 孙建国. Kirchhoff型偏移理论的研究历史、研究现状与发展趋势展望:与光学绕射理论的类比、若干新结果、新认识以及若干有待于解决的问题[J]. 吉林大学学报(地球科学版),2012,42(5):1521-1552.
Sun Jianguo. The History, the State of the Art and the Future Trend of The Research of Kirchhoff-Type Migration Theory: A Comparison with Optical Diffraction Theory, Some New Understanding and Some Problems to be Solved[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(5): 1521-1552.
[2] 孙建国. 高频渐近散射理论及其在地球物理场数值模拟与反演成像中的应用:研究历史与研究现状概述以及若干新进展[J]. 吉林大学学报(地球科学版),2016,46(4):1231-1259.
Sun Jianguo. High-Frequency Asymptotic Scattering Theories and Their Applications in Numerical Modeling and Imaging of Geophysical Fields: An Overview of the Research History and the State-of-the-Art, and Some New Developments[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(4): 1231-1259.
[3]Vidale J E. Finite-Difference Calculations of Travel-Times[J]. Bulletin of the Seismological Society of America, 1988, 78: 2062-2076.
[4]Vidale J E. Finite-Difference Calculations of Travel-times in Three Dimensions[J]. Geophysics, 1990, 55: 521-526.
[5] Rawlinson N, Sambridge M. Multiple Reflection and Transmission Phases in Complex Layered Media Using a Multistage Fast Marching Method[J]. Geophysics, 2004, 69(5): 1338-1350.
[6] de Kool M, Rawlinson N, Sambridge M. A Practical Grid-Based Method for Tracking Multiple Refraction and Reflection Phases in Three-Dimensional Heterogeneous Media[J]. Geophysical Journal International, 2006, 167(1): 253-270.
[7] 孙章庆,孙建国,王雪秋,等. 三维复杂山地多级次群推进迎风混合法多波型走时计算[J]. 地球物理学报,2017,60(5):1861-1873.
Sun Zhangqing, Sun Jianguo, Wang Xueqiu, et al. Computation of Multiples Seismic Traveltime in Mountainous Areas with Complex 3D Conditions Using Multistage Group Marching up Wind Hybrid Method[J]. Chinese Journal of Geophysics, 2017, 60(5): 1861-1873.
[8] 唐小平,白超英. 最短路径算法下三维层状介质中多次波追踪[J]. 地球物理学报,2009,52(10):2635-2643.
Tang Xiaoping, Bai Chaoying. Multiple Ray Tracing Within 3-D Layered Media with the Shortest Path Method[J]. Chinese Journal of Geophysics, 2009, 52(10): 2635-2643.
[9] Sun Jianguo, Sun Zhangqing, Han Fuxing. A Finite Difference Scheme for Solving the Eikonal Equation Including Surface Topography[J]. Geophysics, 2011, 76(4):T53-T63.
[10] 石秀林,孙建国,孙辉,等. 基于波前构建法的时间域深度偏移:Delta波包途径[J]. 吉林大学学报(地球科学版),2016,46(6):1847-1854.
Shi Xiulin, Sun Jianguo, Sun Hui, et al. Depth Migration in Time Domain Using Wavefront Construction: Delta Packet Approach[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(6): 1847-1854.
[11] 石秀林,孙建国,孙辉,等.基于delta波包叠加的时间域深度偏移[J].地球物理学报,2016,59(7):2641-2649.
Shi Xiulin, Sun Jianguo, Sun Hui, et al. The Time Domain Depth Migration by the Summation of Delta Packets[J]. Chinese Journal of Geophysics, 2016, 59(7), 2641-2649.
[12] 孙建国,何洋. 基于波前构建的射线追踪:一种Java实现[J].吉林大学学报(地球科学版),2007, 37(4):814-820.
Sun Jianguo, He Yang. Ray-Tracing Based on Wavefront Construction: A Java Implementation[J]. Journal of Jilin University (Earth Science Edition), 2007, 37(4): 814-820.
[13] 韩复兴, 孙建国, 王坤. 速度模型光滑分析[J]. 吉林大学学报(地球科学版),2011, 41(5): 1610-1616.
Han Fuxing, Sun Jianguo, Wang Kun. Analysis of Velocity Model Smoothing[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(5): 1610-1616.
[14] 韩复兴,孙建国,孙章庆. 波前构建法研究现状[J]. 地球物理学进展,2011,26(3): 1045-1051.
Han Fuxing, Sun Jianguo, Sun Zhangqing. Research Status of the Wavefront Construction Method[J]. Progress in Geophysics, 2011, 26(3): 1045-1051.
[15] 张东,张婷婷,乔友锋,等.三维旅行时场B样条插值射线追踪方法[J]. 石油地球物理勘探,2013,48(4):559-566.
Zhang Dong, Zhang Tingting, Qiao Youfeng, et al. A Ray Tracing Method Based on B-Spline Traveltime Interpolation[J]. Oil and Gas Prospecting, 2013, 48(4):559-566.
[16] 张婷婷,张东,邱达. 三维层状介质中基于走时梯度的多次波射线追踪[J]. 石油地球物理勘探,2014,49(6):1097-1105.
Zhang Tingting, Zhang Dong, Qiu Da. Multiple Ray Tracing in 3D Layered Media Using the Traveltime Gradient Method[J]. Oil and Gas Prospecting, 2014,49(6):1097-1105.
[17] 张婷婷,邱达,张东. 一种改进的三维旅行时梯度射线追踪方法[J]. 石油地球物理勘探,2016,51(5):916-923.
Zhang Tingting, Qiu Da, Zhang Dong. A Modified 3D Traveltime Gradient Ray Tracing Method[J]. Oil and Gas Prospecting, 2016,51(5):916-923.
[18] Press W H, Teukolsky S A, Vettering W T, et al. Numerical Recipies in FORTRAN[M]. Cambridge: Cambridge University Press, 1992.
[19] 蒋迅,王淑红. 切比雪夫和切比雪夫多项式的故事[J]. 科学, 2016, 68(4): 54-58.
Jiang Xun, Wang Shuhong. The Story of Chebyshev and Chebyshev Polynomials[J]. Science, 2016, 68(4): 54-58.
