预期冲击、房地产部门波动与货币政策

华昱

摘要：本文建立了一个两部门新凯恩斯动态随机一般均衡模型，并加入针对房价预期形成的适应性学习部分，重点考察预期冲击对房地产部门和宏观经济波动的影响。贝叶斯估计结果表明：首先，预期冲击会显著影响房价与房地产投资，并通过房地产部门将波动传导到经济中的其他部门；其次，会引起对非房地产部门投资的“挤出”效应；再次，对非房地产业的实际变量的影响主要集中在短期，在长期则较为有限；最后，房屋供给冲击、预期冲击和货币冲击能够解释房价和房地产投资在整个样本期的大部分波动。此外，对最优货币政策的分析显示，在存在预期冲击的环境中，对房价做出反应的货币政策有助于降低經济波动所引起的损失。

关键词：预期冲击；DSGE模型；适应性学习；最优货币政策；房价波动；贝叶斯估计

文献标识码：A 文章编号：1002-2848-2018（02）-0048-09

一、 引 言

过去十年中，中国大部分城市经历了房价的快速增长，在刺激经济增长的同时也引发了社会对于市场过热的担忧。房地产部门的发展对于宏观经济的稳定与增长以及社会福利有重要意义，因此房价的变动也是各界关心的重点。研究普遍认为房价在长期主要受经济基本面影响[1-7]，但是在短期，房价的快速上涨已经脱离经济基本面，住房市场出现了过度繁荣，政策与投机因素显著影响房价的变动[8-12]。

在影响房价的短期因素中，公众预期是一个非常重要的因素，它会直接影响短期中的投资行为而造成市场波动。Shiller[13]认为预期导致的波动是所有资产市场的天性，房屋市场也不例外。预期有时受到诸如过度信心、片面信息、羊群效应等非经济基本面因素的影响，导致资产价格在短时间内出现波动。随着今天信息技术的飞速发展，获取信息的便利性与多样性增加了市场交易中的噪声，公众的预期形成过程易受到其他市场参与者和市场整体氛围的影响，产生大幅波动，这在资本市场表现尤为明显。因此，公众预期对于房地产市场短期波动的影响在信息社会中显得愈发重要。

那么，公众对房屋市场预期的变化在多大程度上带来房地产部门的波动？此外，这种影响是否通过房地产部门扩散到其它领域而造成更大范围的经济波动？本文对这些问题进行了逐一探讨。

宏观经济学研究预期变化的方式之一是采用偏离理性预期的分析框架，比如引入适应性预期模型来刻画预期形成的过程。Milani[14]考察了美国消费者信心的变化如何影响总产出、总消费与总投资。为刻画消费者信心的变动，采用了在DSGE模型中嵌入适应性预期模型的方法。Muellbauer and Murphy[15]在适应性预期基础上建立了一个房地产投机模型，研究预期引发的投机对英国房价波动的影响，由此带动了相关领域的进展。国内在这方面已有初步研究，况伟大[16]、高波、王文莉、李祥[17]采用适应性预期模型重点研究了预期对国内房价以及房价租金比的影响。不过，这些研究都是建立在部分均衡模型的基础上，尚未涉及预期变化如何通过影响房地产部门而导致宏观经济中其他变量出现波动。

本文沿袭Milani[14]的研究思路，在一般均衡框架中纳入适应性学习过程来研究预期变化对房地产部门和宏观经济的影响。采用适应性预期模型一方面保证了均衡的唯一性，减少研究结果对多重均衡的依赖；另一方面是因为适应性预期比较符合资本市场形成预期的某些重要特征。Shiller[13]曾指出，如果人们之间的决策行为是相互独立的，那么错误的想法会在群体中被平均掉，不会出现系统性偏差，就不会对资产价格产生影响。但是，如果有相当一部分人持有相似的、有误的信念时，这种信念会在市场交易者间相互传染从而引发市场的繁荣与衰退。在宏观经济处于增长阶段且房屋市场处于繁荣的气氛中，人们普遍会对未来产生乐观情绪，当前房价的上涨会引发未来房价将进一步上涨的信念。这种信念在人群中传播并被逐步强化。此时，预期的自我实现机制（selffulfilling mechanism）就会启动。对未来房价上涨的预期会吸引更多投资者参与到房地产市场的交易中。投资的增加会拉动房价进一步上涨，于是最初的预期成为了现实，并进一步催生出新一轮的看涨预期，从而形成一种自我实现的反馈回路。这种预期自我实现机制在市场持续繁荣或衰退时表现尤为明显。

由于预期自我实现机制高度依赖过去发生的事情，因此引入适应性预期模型来解释预期形成较为合理，因为它强调人们假设将来的情况与过去相似，并基于过去的状态形成预期，同时允许出现系统性预期误差。

Pigou[18]较早地提到了预期与宏观经济周期的关系，并强调企业家们对于未来所产生的错误的乐观或悲观预期是经济波动的重要力量之一。阿克洛夫和希勒[19]则指出美国住房市场的起伏、住房投资的波动与动物精神理论存在密切关联。

与现有文献相比，本文的创新之处在于扩展了动态随机一般均衡模型，纳入了刻画预期形成的适应性学习部分。这样做既可以考察预期冲击对房地产部门的影响，同时可以在一般均衡的框架下考察这种波动是否会传导到经济的其他领域，弥补了部分均衡分析的不足。本文剩余部分展开如下：第二部分介绍理论模型与研究思路，第三部分说明参数估计方法与结果，第四部分为基于参数估计的扩展分析与稳健性检验，第五部分为结论与建议。

二、包含预期的一般均衡模型

（一）基准模型

本文的模型框架建立在一个包含了房地产部门的DSGE模型基础之上。基准模型还包括消费者部门、最终产品部门、中间生产部门和货币当局。为简化分析，假设政府征收定额税并遵循李嘉图等价财政原则，因此财政政策对经济变量总量没有影响。所以无需讨论财政政策效应，也无需设定财政部门。经济由一个代表性家庭、一个代表性最终产品生产商、一个中间产品生产商、政府和货币当局共同构建而成。家庭向中间产品生产商提供劳动并出租资本，由此获取劳动与资本报酬；中间生产商生产的产品提供给最终产品生产商，用于生产消费品和资本品，并假设资本品和消费品之间可以完全转化；同时，家庭还拥有企业，所以企业利润也归家庭所有；货币当局按照泰勒规则制定货币政策。具体模型如下：

1.代表性家庭

假设经济中存在大量连续同质家庭，构成测度为1的连续统（continuum of measurement）。代表性家庭最大化终身效用的贴现流：

E∑∞t=0βtln（Ct-γcCt-1）+lnht-11+η（n1+ξc，t+n1+ξh，t）1+η1+ξ（1）

其中，β为时间贴现因子，γc为消费习惯因子，η为劳动供给弹性的倒数，Ct为t期的消费，ht为t期购置房屋的消费，nc，t为t期消费品部门的劳动供给，nh，t为t期房地产部门的劳动供给。η为劳动供给弹性倒数，ξ為劳动力在两部门间的替代弹性。

家庭预算约束如下：

Ct+Ic，t+Ih，t+qtht+Bt-1Rt-1πt+a（uc，t）kc，t-1+a（uh，t）kh，t-1≤∑i=c，hwi，tni，t+∑i=c，hri，tui，tki，t-1+Bt+qt（1-δh）ht-1+Πt（2）

其中，qt是用消费品衡量的房屋价格，Ic，t是t期消费品生产部门投资，Ih，t是t期房地产部门投资，Bt为t期购入的政府债券，Rt-1为名义利率或资本收益率，kc，t-1为（t-1）期期末消费品部门的资本存量，un，t为t期消费品部门的资本利用率，a（un，t）为消费品部门每单位资本使用成本，kh，t-1为（t-1）期期末房地产部门资本存量，uh，t为t期的消费品部门资本利用率，a（uh，t）为房地产部门每单位资本使用成本，wi，t为实际工资率，ri，t为实际资本租金，δh为房屋折旧率，Πt为企业利润。

2.代表性企业

假设经济中存在大量连续同质企业，构成测度为1的连续统。沿用Iacoviello and Neri[20]的设定，假设代表性最终产品企业同时生产两种产品——消费品和房屋。两种产品的生产函数如下：

消费品部门生产函数：

Yt=Ac，t（uc，tkc，t）αn1-αc，t（3）

其中，消费品生产过程中投入资本与劳动，α与（1-α）是两种要素的投入产出弹性。Ac，t是消费品部门全要素生产率冲击，服从AR（1）过程。

lnAc，t=ρAlnAc，t-1+σAεAt（4）

房地产部门生产函数：

IHt=Gtlμlt（uh，tkh，t）μhn1-μh-μlh，t（5）

其中，IHt为每期新建房屋数量，lt为土地投入。μl、μh、1-μh-μl分别为土地、资本和劳动的投入产出弹性。Gt为房地产部门供给冲击，服从AR（1）过程：

lnGt=ρGlnGt-1+σGεGt（6）

在一些研究中，这一冲击被定义为房地产部门的全要素生产率冲击[21-22]。在中国，造成房地产部门供给波动的原因除了涉及房地产部门生产率的变化，还有一个很重要的原因就是房地产部门相关政策的变化。因此，如果把Gt仅仅解释为房地产部门的全要素生产率冲击，有可能会高估该冲击的影响。所以本文把它定义为房地产部门供给冲击。

给定消费品部门和房地产部门的生产函数，企业的目标是最大化利润

Πt=Yt+qtIHt-∑i=c，hwi，tni，t-∑i=c，hwi，tn′i，t-∑i=c，hri，tui，tki，t-Rl，tlt（7）

其中Rl，t为土地租金。此处需要对土地租金进行探讨。理论上，完全竞争市场中土地租金应该等于土地的边际产出，但我国的土地租金不完全由市场决定，所以现实中租金并不等于边际产出。在房地产部门生产函数中加入房地产部门供给冲击，可以在一定程度上解决这个问题。当企业利润最大化时可以得到等式GtμlqtIHt=Rl，t，μlqtIHt为完全竞争市场上土地的边际产出。可以看到房地产部门供给冲击Gt的存在等于在土地租金和边际产出之间放入了一个楔子（wedge），当存在供给冲击时，二者就不相等。而房地产供给冲击中包含了政策的变动，这意味着土地租金既受到市场因素的影响，也会受到政策变动的影响。从这个角度看，本文对房地产供给冲击和对土地租金的处理都比较符合现实。

消费品和房地产部门的资本运动方程分别为：

kc，t=（1-δck）kc，t-1+φt1-sIc，tIc，t-1Ic，t（8）

kh，t=（1-δhk）kh，t-1+1-sIh，tIh，t-1Ih，t（9）

其中，δck和δhk分别为两种资本的折旧率，s（·）为投资调整成本。φt为投资专有技术冲击

因为投资专有技术通常是与设备制造、非IT领域的软件、计算机及其它通信与信息技术装备密切相关的，而对房地产部门的影响相对较小，所以此处假设投资专有技术只发生于消费品部门的资本运动过程中。

，服从AR（1）过程：

lnφt=ρφlnφt-1+σφεφt（10）

其中，ρφ为自回归系数，εφt服从均值为0、方差为σφ独立同分布的随机过程。令

sIh，tIh，t-1=ψhIh，tIh，t-1-δhk2，

sIc，tIc，t-1=ψcIc，tIc，t-1-δck2，其中ψh和ψc为投资调整成本弹性。

3.名义粘性

假定消费品价格存在粘性

由于房屋价格，尤其是二手房价格，相对于消费品价格变动更加灵活，因此我们只假定消费品部门存在价格粘性。

，经济中存在着连续统为1的零售商，彼此为垄断竞争。市场对零售商的需求函数为yit=pitpt-θtYt，其中θt为产品间的需求替代弹性，随时间变化，视为成本加成冲击，服从AR（1）过程。零售商遵循Calvo定价法则，每一期只有（1-θp）的零售商可以重新制订最优价格，其余企业根据上一期的通胀率对产品进行指数化调整。由此可以得到价格运动法则：

1=θpπKt-1πt1-θt+1（1-θp）（π*t）1-θt（11）

其中，π*t=p*t/pt，p*t为均衡价格，κ是Calvo定价中的通货膨胀调整指数。

工资的决定过程与Calvo定价相似。家庭是异质性劳动的供给者，最终通过一个处于完全竞争的企业，将异质性劳动力转化为消费品和房屋生产所需的劳动力。各生产部门对劳动力的需求函数为nit=witwt-Nt。其中，nit为异质性劳动力的供给，Nt为各部门的劳动力总需求，wit为异质性劳动力的工资，wt为工资总水平，为异质性劳动力的替代弹性。每一期有（1-θw）的家庭可以重新制定最优工资，其余家庭根据上一期的通胀率对工资进行指数化调整。由此得到两部门的工资运动法则：

w1-cct=θwπκct-1πt1-cw1-cct-1+（1-θw）（w*ct）1-c（12）

w1-hht=θwπκht-1πt1-hw1-cht-1+（1-θw）（w*ht）1-c（13）

其中，κc和κh为通货膨胀调整指数，w*ct和w*ht为两部门的均衡工资。

4.中央银行

我国货币政策的制定主要考虑通货膨胀预期和经济增长指标。因此，设定中央银行遵循如下的泰勒规则：

Rt=Rρrt-1πρπtGDPtGDPt-1ρy1-ρrmt（14）

其中，GDPt=Yt+qtIHt，ρr、ρπ和ρy为货币政策对于利率、通货膨胀和产出增长率的反应参数。mt为货币政策冲击，服从方差为σm随机独立同分布。

在此基础上可以得到模型的均衡系统。稳定状态时，假设资本利用率unt+1=uet+1=1；资本使用成本a（1）=0，且a′和a″都大于零；由于假定模型中技术增长是平稳的，不含有增长趋势，因此设定投资调整成本s（1）=s′（1）=0；此外，令qt=Qt/λt，即托宾Q。为简化模型，假定在稳定状态下，两种资本的托宾Q皆等于1。最后，将土地供给量标准化为单位1，即lt=1。在这些假定基础上，得到包含26个动态方程的线性系统

篇幅有限，此处省略，有兴趣可向作者索取。

。

（二）包含预期的扩展模型

接下来为考察公众预期变化对宏观经济的影响，将基准的DSGE模型进行扩展，加入预期形成的适应性学习过程，个体的可观测行动法则（Perceived Law of Motion，PLM）可以写作：

yt=At+Btyt-1+ut（15）

ut是预测误差。此处的学习参数（learning parameter）At和Bt未知，随时间变化而逐步演化。每一期，代理人会更新对At和Bt的认识，从而得到新参数值。yt为需要考察的因变量，在本文中，yt代表房价。现实中房价的上涨或下跌受到预期自我实现机制的影响。当房价处于快速上升期，人们会产生未来房价还会进一步上涨的预期，因此資本流入房地产市场，投资增加导致房价持续上升，并引起下一轮的乐观预期。所以公众预期形成过程是一种适应性学习过程。

根据Milani[14]，学习参数的递归过程可以写作：

t=t-1+gtR-1txt（yt-x′t-1t-1）（16）

Rt=Rt-1+gt（xtx′t-Rt-1）（17）

其中，t=（At，Bt）′，xt=（1，yt），Rt为精确矩阵（precision matrix）。第一个方程描述代理人更新对于t的信念的过程；第二个方程描述代理人更新对于Rt的信念的过程。gt为收益参数，是代理人在递归求解学习参数时，赋予新数据的权重，通常被设定为等于1/t。依照惯例，本文假定gt为常数。

根据式（15）、（16）和（17）可以得到一个关于房价qt预期的表达式，即

E*tqt+1=（I+Bt）At+B2tqt-1+st（18）

注意，这里的预期E*t和DSGE模型中的Et有重要区别。预期E*t包含着对未来房价预期的扰动。由此，假如适应性学习部分可以得到一个明显异于理性预期模型的地方：在理性预期模型中，所有的波动都是由与经济基本面相关的外生冲击引起的，而加入了适应性预期后，经济波动还可以源自对预期的冲击。st衡量的就是这种预期冲击，服从AR（1）过程：

lnst=ρslnst-1+σsεst（19）

适应性学习模型的一个问题是对gt值的确定。现有研究通常采用人为设定或校准法确定该值，这导致估计结果对该变量取值比较敏感[14]。本文采用贝叶斯法估计该参数，可以在一定程度上规避人为设定参数值的主观性，确保结果的稳健。

三、参数估计方法与结果

本文选取2000年至2013年季度人均消费cobt、消费品部门人均投资icobt、房地产部门人均投资ikobt，房地产预期价格qobt、通货膨胀率piobt，利率Robt作为贝叶斯估计所需的观测变量。用于贝叶斯估计的测算方程如下，第二个括号里的变量在模型中为对数线性化后的变量，代表实际值偏离稳态值的百分比：

Yt=cobt

icobt

ikobt

piobt

qobt

Robt=

ct-ct-1

ict-ict-1

ikt-ikt-1

pit

qt-1-qt-2

Rt（20）

通货膨胀率为季度CPI的环比增长率。消费、消费品部门投资与房地产部门投资的观测值先采用国家统计局公布的月度数据，以2010年为基期利用月度CPI作为价格平减指数进行调整，再将月度数据汇总为季度的消费与投资数据。月度、季度CPI数据军来源于美国联邦储备银行圣路易斯分行经济数据库。利率为央行一年期贷款基准利率的季度平均值，数据来源于中国人民银行官网。参考已有文献[16-17]，采用滞后一期的房价一阶差分作为房地产预期价格的代理变量。除利率与通胀率外，所有变量皆除以14岁以上人口，得到人均变量。由于没有季度人口数据，本文采用求几何级数的方法先利用年度人口增长率得到季度人口增长率，再利用年度人口与季度人口增长率推算出季度人口。年度14岁以上人口与增长率数据来源于《中国人口年鉴》。所有变量都经过季节性调整。

模型中的35个结构参数分为两组。其中一组参数值通过校准法确定

依照惯例，这组参数主要涉及无法分离识别、现有数据可以估计的大比率（Greatratios）、以及可以从稳态关系中推导出其值的参数。

，包括：消费品和房屋生产函数中的产出弹性α、μl和μh、房屋折旧率δh、消费品部门的资本折旧率δck、房地产部门的资本折旧率δhk、家庭的时间贴现因子β。参照现有文献，消费品生产函数中的资本产出弹性设定为055。对于时间贴现因子β，国内外大多数文献取值都在090至099[21]。由于在稳定状态下存在等式Rβ=1，在本文的样本时间跨度中，央行一年期贷款基准利率平均值为631%

数据来源于中国人民银行2015年10月24日发布的金融机构人民币贷款基准利率历史数据。

，因此季度利率为108%，由此推得β为093。消费品部门资本季度折旧率设定为00026，房地产部门资本季度折旧率为00024，房屋折旧率0003，这与α一起，保证了系统在稳定状态时，消费与GDP比值、消费品生产部门投资与GDP比值、房地产部门投资与GDP比值分别为03、045和015，较接近真实数据值。房地产部门生产函数的资本产出弹性设为004，保证了稳定状态下房地产部门的投资与GDP比值为015，较接近真实数据值。在稳定状态下，存在等式μl=RllqIH，意味着土地产出弹性等于土地成本与房屋销售的比值。根据国家统计局2000年至2013年的数据，该比值的年度均值为0095。所以，土地产出弹性设为0095。表1总结了采用校准法确定的参数值。

表1 参数校准值

模型中的其他结构参数值通过贝叶斯法估计得到，在确定这些参数的先验分布函数、均值与标准差的时候，借鉴了国内外相关文献中的研究设定，包括消费习惯因子、劳动供给弹性、两部门劳动替代弹性、泰勒规则中的反应系数、投资调整成本函数参数、资本使用成本函数在稳态时的曲率。投资调整成本函数参数服从均值为4、方差为4的Gamma分布，其90%密度区间包含了大部分经典文献中的估计结果[20]。所有外生冲击过程中的AR（1）自回归系数服从Beta分布；所有的新息方差服从倒置的Gamma分布，这个假定保证了方差为正。表2显示了先验分布函数的主要特征与MetropolisHastings算法随机抽样100000次的结果，其中50000～100000次的抽样被用于做推断。

从贝叶斯估计结果上看，真实数据在用于估计时提供了一些有效信息。两部门间的劳动替代弹性ξ的估计值为0975，为正且小于1，说明房地产部门与消费品部门间存在着一定程度的行业特性，但程度并不明显。劳动替代弹性估计值为0429。这两个弹性系数的后验均值与先验值较为一致，说明真实数据并没有为参数估计提供较多信息。这可能与本文在估计时缺乏劳动时间与工资方面的数据有关。收益不变参数g为0019。这一方面证明了代理人在大部分情况下是理性的，另一方面也暗示市场参与者受到过去经济形势发展的影响并对此产生依赖，在此基础上形成对未来的预期，所以预期呈现出了惯性。此外，理性预期模型在匹配模拟结果的持续性与真实数据的持续性时，比较依赖模型中不同类型的粘性假设。而在引入了适应性学习的概念扩展了基准模型之后，可以看到，传统上用以生成数据持续性的消费习惯、工资指数估计值都不太高。换句话说，扩展后的模型较少地依赖机械化的粘性假设，这也是采用适应性学习模型的一个优势。

表2 贝叶斯估计参数的先验与后验分布

图1 主要宏观经济变量对预期冲击的脉冲反应

四、扩展分析与稳健性检验

这一部分进行基于参数估计结果的扩展分析与相关参数的稳健性检验。

（一）脉冲反应函数

此处重点考察预期冲击对主要宏观经济变量的影响，其余外生冲击的脉冲反应与经典文献的结果基本吻合，在此不再赘述。图1显示一个标准差的正向预期冲击对主要宏观经济变量的脉冲反应函数。当出现正向预期冲击时，即当人们对未来房地产价格产生乐观预期时，房地产部门的投资和房价出现了明显的上升，由此带来的影响也具有持续性。房价所呈现出的正向且瞬时的脉冲反应表明了预期存在自我实现机制。由于房地产投资的显著增加，总产出也相应地上升。但是，另一方面非房地产业投资出现了一定程度的下降，这可能是因为房地产业投资的“挤出效应”导致的。由于存在着对于房地产业投资收益上升的预期，大量的资本会涌入该行业，这导致流入非房地产业资本的下降。但是随着经济总量的扩张，社会总资本的增加，非房地产业的投资又经历了一个逐渐上升并最终回到均衡的过程。但是这也说明了在长期中，房地产业投资的增加对于经济中其他行业的拉动作用是有限的。消费、利率和通货膨胀都经历了一个先升后降的过程。但是除消费外，利率和通货膨胀水平并没有回归到原先的均衡水平，而是收敛到了一个新的水平。这与房价和房地产投资在预期冲击下所呈现出的持续的脉冲反应是一致的。这在一定程度上表明，预期冲击对宏观经济中的名义变量的影响较为显著，而对非房地产业的实际变量的影响主要集中在短期，在长期则较为有限。

（二）方差分解

研究经济周期波动时，人们比较关心的另一个问题是，主要经济变量的波动在多大程度上可以由各类外生冲击来解释。可以通过对经济变量进行无条件方差分解找到一些答案。表3和表4描述了短

表3 短期方差分解結果

表4 长期方差分解结果

期与长期各变量的无条件预测误差方差分解。其中，第一行的符号分别代表消费品部门技术冲击、房屋供给冲击、货币政策冲击、投资专有技术冲击、成本加成冲击和预期冲击。

从整体上看，投资专有技术冲击和成本加成冲击是导致总产出波动的主要原因。消费品部门技术冲击、成本加成冲击、货币政策冲击是影响消费变化的主要因素。成本加成冲击主要是通过影响通货膨胀预期和工资预期，进而通过收入效应影响当期消费。事实上，脉冲反应结果也显示一个标准差的正向成本加成冲击会引起消费下降04个百分点。引起消费品部门投资波动的主要因素是投资专有技术冲击，而房地产部门的投资波动在短期主要是由房地产部门供给冲击、预期冲击以及货币政策冲击引起的，而在长期中，依旧是房屋供给冲击起主导作用。此外，房屋价格按程度依次受到预期冲击、房屋供给冲击和货币政策冲击的影响。最后，成本加成冲击解释了通货膨胀短期632%的波动以及长期449%的波动，是导致通货膨胀变化最重要的因素。

（三）反事实模拟

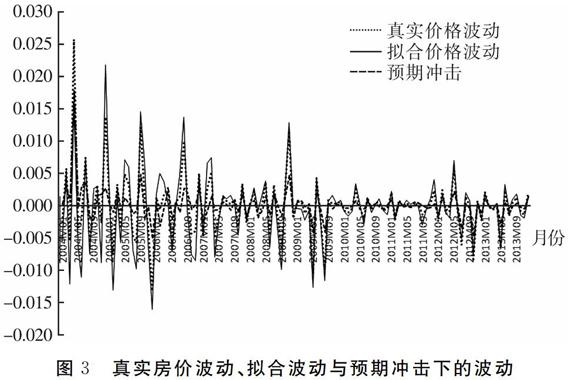
由于方差无条件分解无法从整个样本期对外生冲击的重要性以及解释力给予全面的评价，所以本文又进行了反事实模拟。图2和图3刻画了房地产部门投资和房屋价格的真实波动、基于模型估计得到的波动以及只存在预期冲击时

图2 房地产投资真实波动、拟合波动与预期冲击下的波动

图3 真实房价波动、拟合波动与预期冲击下的波动

的模拟波动。结果显示，当经济同时受到六类外生冲击时，房地产部门投资和房屋价格波动的真实值与估计值的走势较为吻合，一定程度上证明本文的模型设置与参数估计较准确地捕捉到了真实经济波动的特征。此外，当只有预期冲击时，房地产部门投资和房屋价格的真实波动与估计值也非常接近。这与之前方差分解的结果一致，说明预期冲击是导致房地产部门投资和房屋价格波动最重要的外生因素。

（四）模型设定合理性检验

本文调整了一些结构参数的先验分布初始值，重新估计模型，随后比较各主要经济变量在采用不同模型进行估计时得到的模拟方差，由此考察模型设定的合理性。表5显示了估计结果。此处调整了价格与工资调整过程中的参数值，假设价格和工资调整更加灵活。同时也估计了不存在预期冲击时的模型。结果显示，总体上，基准模型中的模拟方差与真实数据方差最为接近，在一定程度上支持了本文模型的设置。

表5 模型设定合理性检验结果

（五）最优货币政策选择

由于房地产价格波动会影响宏观经济中的主要变量，因此接下来本文从最优货币政策的角度来讨论央行的货币政策是否需要对房价波动做出反应。假定包含房价的泰勒规则为：

Rt=Rρrt-1πρπtGDPtGDPt-1ρyqtqt-1ρq1-ρrmt（21）

为了评价最优货币政策，假定央行的损失函数为：

LF=φvar（yt）+（1-φ）var（πt）（22）

var（yt）和var（πt）分别代表产出与物价的无条件方差，φ为二者分别在损失函数中所占的权重。央行的目标是在由模型推导出的一阶条件的约束下，最小化损失函数，以此判定泰勒法则中的结构参数。此处参考现有文献[22]设定反应参数ρq的初始值为01076，然后采用迭代最优算法搜寻最小目标值。

本文选取了一系列不同的权重值φ，对两种不同的泰勒规则进行估计，得到了不同权重值下的产出与通胀方差，进而得到不同货币规则下的效率前沿曲线。图4中的虚线效率前沿曲线对应的是对房价做出反应的泰勒规则，实线效率前沿曲线对应着不对房价做出反应的泰勒规则。效率前沿曲线位置越靠右方，代表央行的货币政策引起的福利损失越高。可以看出，给定央行损失函数，当货币政策对房价做出反应时，由经济波动带来的损失有所降低。如何理解这样的结果？在本文中，预期冲击是一个导致房价波动的重要因素。当货币政策对房价做出反应时，相当于对公众做出了一种承诺，公众会对此形成稳定的预期。所以货币政策在一定程度上可以起到熨平预期波动的作用，从而减少宏观经济中各主要变量的波动。因此，可以看到，在一个包含了预期冲击的模型中，最优货币政策应该倾向对房价波动做出反应。

图4 效率前沿曲线

五、结论与建议

综上所述，预期冲击会显著影响房地产投资与房屋价格，同时会通过房地产部门将波动传导到宏观经济的其他领域。具体来看：首先，正向的预期冲击会在短时间内显著提高房地产部门投资、房屋价格以及总产出；其次，预期冲击也会影响非房地产部门的变量，包括消费与物价水平，尤其在短期房地产部门投资上升会挤出非房地产部门投资，不过这些影响主要集中在短期，在长期则较为有限，在长期中，房地产业投资的增加对于经济中其他行业的拉动作用是有限的；再次，无条件方差分解的结果显示，短期中预期冲击是导致房地产市场波动的主要原因，但是长期中来自供给一侧的外生冲击是带来房地产部门波动的更主要原因；最后，在考虑存在预期冲击的情况下，货币政策应该对房价波动做出反应，有利于降低由经济波动所引起的损失。此外，基于样本期的反事实模拟的结果进一步说明了加入预期冲击后模型可以较好地拟合真实数据。稳健性检验结果也支持对模型的设定。

从全国范围来看，预期对住房价格波动的解释力度在短期超过经济基本面，市场主体对未来的预期是影响房价走势的重要因素，政府应考虑加强房地产市场参与主体的预期管理。此外，研究表明房屋供给冲击是另一个在短期和长期都对房地产部门主要变量产生显著影响的因素。相应的政策启示是在进行房地产市场调控时，不仅需要对需求方进行管控，从长期来看对供给方的调节更加重要，比如适当增加土地供应量将有助于减少房地产部门的波动。

参考文献：

[1] 张涛， 龚六堂， 卜永祥. 资产回报、住房按揭贷款与房地产均衡价格 [J]. 金融研究， 2006（2）： 1-11.

[2] 姜春海. 中國房地产市场投机泡沫实证分析 [J]. 管理世界， 2005（12）： 71-83.

[3] 许先普， 楚尔鸣. 房价波动、宏观审慎及与货币政策的协调 [J]. 统计与信息论坛， 2017（3）： 62-69.

[4] 赵昕东. 中国房地产价格波动与宏观经济——基于SVAR模型的研究 [J]. 经济评论， 2010（1）： 65-71.

[5] 李梦玄， 曹阳. 我国房地产市场泡沫的测度及成因分析——基于行为金融理论的视角 [J]. 宏观经济研究， 2013（9）： 86-91.

[6] 宋勃， 高波. 利率冲击与房地产价格波动的理论与实证分析： 1998—2006 [J]. 经济评论， 2007（4）： 46-56.

[7] 刘金全， 陈德凯. 我国房地产价格波动与货币政策调控模式研究——基于政策不确定性视角的实证分析 [J]. 当代经济科学， 2017（4）： 51-57.

[8] 安辉， 王瑞东. 我国房地产价格影响因素的实证分析 ——兼论当前房地产调控政策 [J]. 财经科学， 2013（3）： 115-124.

[9] 沈悦， 刘洪玉. 住宅价格与经济基本面： 1995—2002年中国14城市的实证研究 [J]. 经济研究， 2004（3）： 78-86.

[10] 罗刚强， 赵涛. 区域经济基本面与住房价格波动 [J]. 西安电子科技大学学报（社会科学版）， 2010（4）： 73-80.

[11] 李春吉， 孟晓宏. 中国房地产市场结构和价格影响因素的实证分析 [J]. 产业经济研究， 2005（6）： 48-56.

[12] 余华义. 经济基本面还是房地产政策在影响中国的房价 [J]. 财贸经济， 2010（3）： 116-122.

[13] Shiller R J. Irrational exuberance [M]. Princeton， New Jersey： Princeton University Press， 2000： 20-33.

[14] Milani F. Expectations， learning and macroeconomic persistence [J]. Journal of Monetary Economics， 2007， 54： 2065-2082.

[15] Muellbauer J， Murphy A. Booms and busts in the UK housing market [J]. Economic Journal， 1997， 107（445）： 1701-1727.

[16] 况伟大. 预期、投机与中国城市房价波动 [J]. 经济研究， 2010（9）： 67-78.

[17] 高波， 王文莉， 李祥. 预期、收入差距与中国城市房价租金“剪刀差”之谜 [J]. 经济研究， 2013（6）： 100-112.

[18] Pigou A C. Industrial fluctuations [M]. London： Macmillan， 1927： 6-7.

[19] 喬治·阿克洛夫， 罗伯特·希勒. 动物精神[M]. 黄志强， 徐卫宇， 金岚， 译. 北京： 中信出版集团， 2016： 223-233.

[20] Iacoviello M， Neri S. Housing market spillovers： Evidence from an estimated DSGE model [J]. American Economic Journal： Macroeconomics， 2010， 2（2）： 125-164.

[21] 梁斌， 李庆云. 中国房地产价格波动与货币政策分析——基于贝叶斯估计的动态随机一般均衡模型 [J]. 经济科学， 2011（3）： 17-31.

[22] 王云清， 朱启贵， 谈正达. 中国房地产市场波动研究 ——给予贝叶斯估计的两部门DSGE模型 [J]. 金融研究， 2013（3）： 101-113.