边跨非对称的三跨悬索桥振动基频估算方法

杨国俊，杜永峰，郝宪武，李子青，王晓明

(1.兰州理工大学 防震减灾研究所，兰州 730050；2.长安大学 公路学院，西安 710064)

悬索桥的自振频率是许多研究者和设计工程师们普遍关注的结构特性之一[1-3]，而基频是反应结构抗风稳定性和地震动力响应的主要参数，所以利用基频估算公式快速计算频率是悬索桥方案选型和在初步设计阶段计算动力特性不可或缺的一环[4-5]。对于传统的单跨简支悬索桥和三跨连续加劲梁悬索桥，诸多文献初步研究了其相应基频计算公式，其中文献[6]基于单跨简支悬索桥，采用Rayleigh法给出了一阶正对称、反对称竖弯和扭转自振基频的估算公式；刘春华等[7]采用摄动法随机有限元(Stochastic Finite Element Method,SFEM)对桥梁结构的自振频率进行分析；盛善定等[8-9]应用能量法探讨了单跨悬索桥振动时的基频计算公式；谢官模等[10]在盛善定等研究的基础上考虑了吊杆、索夹等的动能后利用Rayleigh法得到了单跨悬索桥竖向振动基频的实用近似计算公式；肖汝诚[4]采用考虑几何非线性的有限元法、通用程序SAP5计算方法和解析法分别计算了吊桥的自振频率，其中解析法推导的公式与文献[6]中的估算公式基本一致；鞠小华等[11]在上述文献的基础上计入主塔刚度对自振频率的影响，采用能量法推导了单跨悬索桥基频估算公式，提出了计入边缆和主塔刚度影响以及考虑实际振型修正后的正对称竖弯基频估算公式；Larsen等[12]基于不考虑主塔刚度影响的假定下，采用Raleigh-Ritz法推导出了三跨连续加劲梁悬索桥的对称竖弯和扭转自由振动基频近似计算公式；鞠小华[13]在Lorsen的研究基础上推导了三跨连续加劲梁悬索桥的反对称竖弯和扭转基频计算公式；焦常科等[14]基于3塔悬索桥采用Lanczos特征值求解法分析了中塔梁间的弹性拉索刚度对竖向振动频率的影响；王本劲等[15-17]提出了考虑中塔刚度影响的3塔或多塔悬索桥的振动基频估算公式。

综上所述，对于传统对称的双塔、多塔以及多跨悬索桥都有相应的基频近似计算公式。由于受地形和地质条件的限制，边跨跨径不对称的三跨非对称悬索桥在国内外不断涌现，如国内的浙江西堠门大桥(578+1650+485)m、香港青马大桥(333+1377+300)m、湖南湘西矮寨特大悬索桥(242+1176+116)m等，英国的亨伯尔桥(540+1410+280)m及土耳其的博斯普鲁斯一桥(231+1074+255)m。由于这类悬索桥边跨跨径的非对称对结构振动频率有不可忽略的影响，所以分析跨径变化对结构自振频率的影响很有必要，而且很少有文献研究边跨跨径非对称的三跨悬索桥基频实用估算公式。虽然有限元法能计算结构的频率，但是悬索桥的复杂性导致有限元建模过程相当繁琐，不便于设计人员快速判断桥梁结构的动力特性。文中基于边跨非对称三跨悬索桥动力特性中自振频率的近似计算公式对该类型桥的动力方面初步设计和设计人员快速判断桥梁结构的振动特性都有较大的帮助作用，另外，实用估算公式以供概念设计或校核有限元计算结果。

1 Rayleigh-Ritz法及基本假定

1.1 基于Rayleigh-Ritz法的频率计算方法

假定振动不受动内力的影响，图1所示的悬索桥竖向固有振动的微分方程为[2]

(1)

在无阻尼固有振动的情况下，桥梁的任一点、任一瞬间的位移可以表示为

v(x,t)=φ(x)sin(ωt+φ)

(2)

式中：φ(x)是假定的能满足桥梁位移边界条件的近似振型函数；ω为与此对应的结构频率；φ为相位差。

根据能量守恒原理[18]可得频率ω的近似公式

(3)

式中：EI(x)和m(x)分别为弯曲刚度和质量分布值函数。

则基频f的计算公式为

(4)

1.2 三跨非对称悬索桥基本假定

为了便于推导边跨跨径不相等的三跨非对称悬索桥自由振动时的竖弯和扭转基频估算公式，其基本假定如下：①忽略材料非线性，所采用的材料均满足胡克定律；②恒载在主缆上沿跨径均匀布置，在恒载作用下主缆的线形为抛物线；③吊索沿跨径均匀稠密布置，并且在振动时不伸长不倾斜；④三跨非对称悬索桥在自由振动时产生较小幅度的位移，且整个过程结构刚度保持不变；⑤主索鞍在主塔上不产生滑动等现象。

为了便于分析边跨非对称性对三跨加劲梁悬索桥动力特性的影响，如图1所示，其中主跨矢高为f2，边跨跨径L1≠L3，文中定义边跨跨径和中跨跨径相关的参数k和l，k表示右边跨跨径与左边跨跨径的比值，即k=L3/L1，l表示左边跨跨径与中跨跨径的比值，即l=L1/L2，采用参数k和l表征三跨连续加劲梁悬索桥的中边跨跨径之间的关系，以此分析跨径相关参数变化对该桥基频的影响。

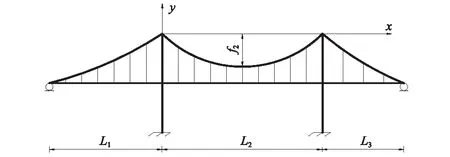
图1 非对称悬索桥布置图Fig.1 Layout of asymmetry suspension bridge

2 三跨非对称悬索桥竖弯基频估算公式

2.1 结构体系势能

根据边跨非对称的三跨连续加劲梁悬索桥结构特点，可得到其一阶正对称和反对称竖弯振型图，分别如图2,3所示。

对于边跨跨径非对称的三跨连续加劲梁悬索桥，H其竖向自由振动的总能量由势能和动能组成，其中由于非对称悬索桥的自由振动是微小的，所以由缆力变化产生的主缆应变能和恒载作用点降低产生的重力势能构成了主缆势能。

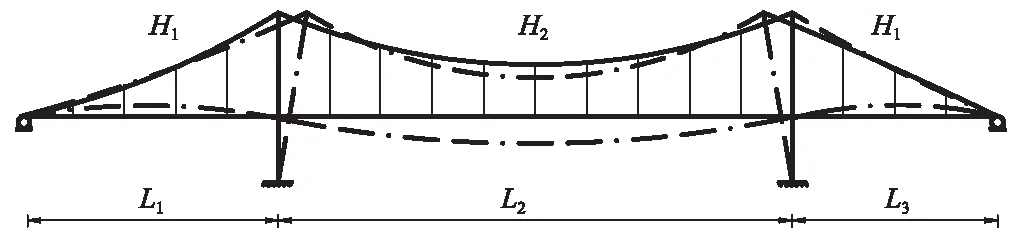
图2 一阶正对称竖弯振型Fig.2 Mode shape of 1st symmetric vertical vibration

图3 一阶反对称竖弯振型Fig.3 Mode shape of 1st anti-symmetric vertical vibration

①对于n跨悬索桥主缆的势能Uc。

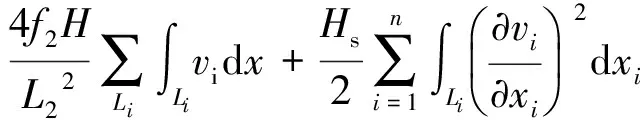
(5)

式中：Uce为缆力变化产生的势能；H为振动引起的主缆水平分力；vi为第i跨加劲梁的振型函数；Ucg为恒载作用点降低产生的主缆重力势能；Hs为恒载作用下主缆的水平拉力。

②对于n跨悬索桥加劲梁的弯曲势能Us

(6)

式中：EIv为加劲梁的抗弯刚度。

则体系总势能U为

(7)

2.2 结构体系动能

由于n跨称悬索桥自由振动的动能由主缆、加劲梁及吊杆的动能组成，所以结构体系总动能为

(8)

式中：Tc、Tg、Th分别为主缆、加劲梁及吊杆动能；mc、mg、mi分别为两主缆缆质量集度之和、顺桥向加劲梁质量集度及第吊索的质量集度。

2.3 正对称竖向弯曲基频估算公式

针对边跨非对称的三跨连续加劲梁悬索桥，其加劲梁的一阶正对称竖弯振型如图4所示，反对称竖弯振型如图5所示。

图4 加劲梁一阶正对称竖弯振型Fig.4 Mode shape of stiffening girder 1st symmetric vertical vibration

图5 加劲梁一阶反对称竖弯振型Fig.5 Mode shape of stiffening girder 1st anti-symmetric vertical vibration

假设满足边中跨边界条件的三跨悬索桥加劲梁振型位移函数为

(9)

式中：A1、A2、A3分别为左边跨、中跨和右边跨竖弯振型函数的振幅。

由于三跨悬索桥的加劲梁是连续梁，根据加劲梁的连续性得其振型函数的导数在分界点处相等，即

当cos(ωt+φ)=1时，

当sin(ωt+φ)=1时，

由Rayleigh-Ritz法可得，

(10)

由式(4)可得边跨非对称的三跨悬索桥正对称竖弯基频为

(11)

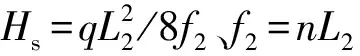
(12)

为了方便计算，忽略量级小的值，由量级分析可知，式(12)第二项比第一项和最后一项小2～3个数量级，近似计算时可忽略不计，故上式可简化为：

(13)

在一般情况下，矢跨比n=0.1，q=mg，若取k=1，则可得边跨对称三跨悬索桥正对称竖弯基频估算公式，

(14)

式(14)与文献[13]中边跨对称的三跨连续加劲梁悬索桥正对称竖弯基频公式一致，表明推导的公式更具有通用性。

若k=1,l→0极限情况时，又因为式(13)根式下第一项比第二项小1个数量级，当忽略此项时，即可得到单跨悬索桥的正对称竖弯自振频率为

(15)

式中：EcAc、EcAc1分别为两侧主缆的抗弯刚度和单侧主缆的抗弯刚度。

式(15)与文献[6]中的单跨悬索桥对称竖弯基频估算公式完全一样，从而验证了边跨非对称的三跨连续加劲梁悬索桥正对称竖弯自振频率估算公式的适用性。

2.4 反对称竖向弯曲基频估算公式

对于边跨非对称的三跨连续加劲梁悬索桥，其加劲梁的一阶反对称竖弯振型如图5所示，假设其满足边界条件的三跨悬索桥加劲梁的振型位移函数为

(16)

同理，由加劲梁的连续性可得，

同理，由Rayleigh-Ritz法可得，

(17)

由式(4)得边跨非对称悬索桥的正对称竖弯基频为

(18)

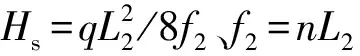
(19)

若取k=1，则可得边跨对称的三跨悬索桥反对称竖弯基频估算公式为

(20)

式(20)与文献[13]中边跨对称的三跨连续加劲梁悬索桥反对称竖弯基频公式一致，表明推导的公式更具有通用性。

3 三跨非对称悬索桥扭转基频估算公式

3.1 结构体系势能

基于边跨不对称的三跨连续加劲梁悬索桥在扭转自由振动时，主缆的相容方程为

(21)

式中：Le为主缆的虚拟长度；

则主缆挠曲势能U3为

(22)

结构体系总势能为

(23)

式中：U1、U2、U3分别为加劲梁约束扭转势能、自由扭转势能及主缆挠曲势能；EJw、GIt分别为加劲梁约束扭转刚度和自由扭转刚度。

3.2 结构体系动能

基于边跨不对称的三跨连续加劲梁悬索桥在扭转自由振动时，结构体系扭转总动能T为

(24)

式中：T1、T2分别为加劲梁旋转动能和挠曲动能；b为两主缆的间距；r为加劲梁质量回转半径；mgr2、mcb2/4分别为加劲梁的扭转惯矩和主缆的扭转惯矩。

3.3 正对称扭转基频估算公式

对于该桥的一阶正对称扭转振动，设其满足边界条件的扭转振型函数为

(25)

式中：B1、B2、B3分别为左边跨、中跨和右边跨扭转振型函数的振幅。

由加劲梁的连续性得，

同理，由Rayleigh-Ritz法可得，

(26)

由式(4)及令J=mgr2+mcb2/4，f2=n·L2，可得边跨非对称三跨悬索桥的正对称扭转基为

(27)

忽略约束扭转，根据边中跨跨径关系L1=lL2、L3=kL1，化简整理式(27)可得

(28)

在一般情况下，矢跨比n=0.1，k=1，边跨对称的三跨悬索桥正对称扭转基频估算公式。

若取k=1,l→0极限情况时，Hsb2/4比GJt小数量级，当忽略此项时，即可得到单跨悬索桥的正对称扭转自振频率计算公式为

(29)

所以式(29)与文献[6，8-9]规范给出的简支单跨悬索桥正对称扭转基频公式完全一样。

为了计算方便，将边跨非对称的三跨加劲梁悬索桥的一阶正对称扭转基频和竖弯基频比值记作扭弯比κ，则正对称扭弯基频比为

(30)

记a=kl+l+1，b=1-k2l2-l2，经简化得，

(31)

3.4 反对称扭转基频估算公式

对于边跨非对称三跨连续加劲梁悬索桥的反对称扭转振动，设其满足边界条件的扭转振型位移函数为

(32)

同理，由加劲梁的连续性得，

同理，由Rayleigh-Ritz法可得，

(33)

则反对称扭转的自振频率为

(34)

根据边中跨跨径关系L1=lL2，L3=kL1，化简整理式(34)可得

(35)

当忽略约束扭转，k=1，得到边跨对称的三跨悬索桥反对称扭转基频估算公式。

若取k=1,l→0极限情况时，可得到单跨悬索桥的反对称扭转自振频率计算公式为

(36)

所以式(36)与文献[6，8-9]中的单跨悬索桥反对称扭转自振频率估算公式是相同的，验证了基于边跨不对称的非对称三跨悬索桥一阶反对称扭转频率估算公式的更具有通用性。

4 公式验证

以某边跨非对称三跨连续加劲梁悬索桥为背景，验证文中推得的估算公式精度。背景桥的算例1跨径布置为(540+1420+280)m，主缆矢跨比n为0.1，两主缆间距为35 m，参数l为0.383，参数k为0.518，加劲梁的泊松比为0.3，算例2跨径布置为(302+888+348.5)m，主缆矢跨比n为0.1，两主缆间距为35.6 m，参数l为0.340，参数为1.154，加劲梁的泊松比为0.3，算例3跨径布置为(328+1385+295)m，主缆矢跨比n为0.1，两主缆间距为37.7 m，参数l为0.237，参数k为0.899，加劲梁的泊松比为0.3，背景桥的其他计算参数取值如表1所示。

将表1中的计算参数代入式(13)、(19)、(28)及(35)，得到上述背景桥的竖弯和扭转振动的基频，同时建立该桥的有限元模型，通过有限元方法计算该背景桥的基频，计算结果如表2所示。

表1 实桥主要结构参数Tab.1 Structural parameters of real project

表2 实桥算例竖弯和扭转振动基频对比Tab 2 Fundamental frequencies comparison of vertical and torsional vibration

算例1边跨非对称的三跨连续加劲梁悬索桥一阶竖弯和扭转自振基频的文中解和有限元解对比分析如图6所示，由表2和图6分析可知，竖弯和扭转自振基频的文中解和有限元解基本吻合，表明推导的该类型桥自振基频计算公式精度较高，两者的误差基本都在10%以内，一阶正对称竖弯振动基频有限元解和文中解的误差是9.2%，一阶反对称竖弯振动基频有限元解和文中解的误差是9.2%，而一阶正对称扭转基频的有限元解和文中解的误差是5.0%，一阶反对称扭转基频的有限元解和文中解的误差是4.4%。

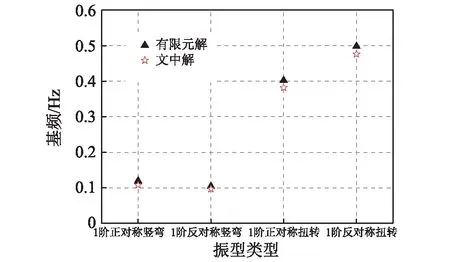
图6 文中解和有限元解的自振频率(算例1)Fig.6 Fundamental frequency calculated by the proposed and the FEM

为了分析跨径相关参数变化对基频的影响，从图7～10分析可知，跨径相关的参数变化对正对称k，l反对称竖弯和扭转基频有较大的影响，当跨径相关的系数、其中之一保持不变，而另一个增大时，正对称、反对称竖弯和扭转的基频基本减小趋势，表明对边跨非对称的三跨连续加劲梁悬索桥而言，当两边跨比不变时，随着边中跨比的增大，竖弯和扭转基频减小，整体刚度减小；当边中跨比不变时，随着两边跨比的增大，同样基频会减小，只是减小的幅度不同而已。

图7 系数变化对正对称竖弯基频的影响Fig.7 Influence of coefficient on symmetric vertical fundamental frequency

图8 系数变化对反对称竖弯基频的影响Fig.8 Influence of coefficient on anti-symmetric vertical fundamental frequency

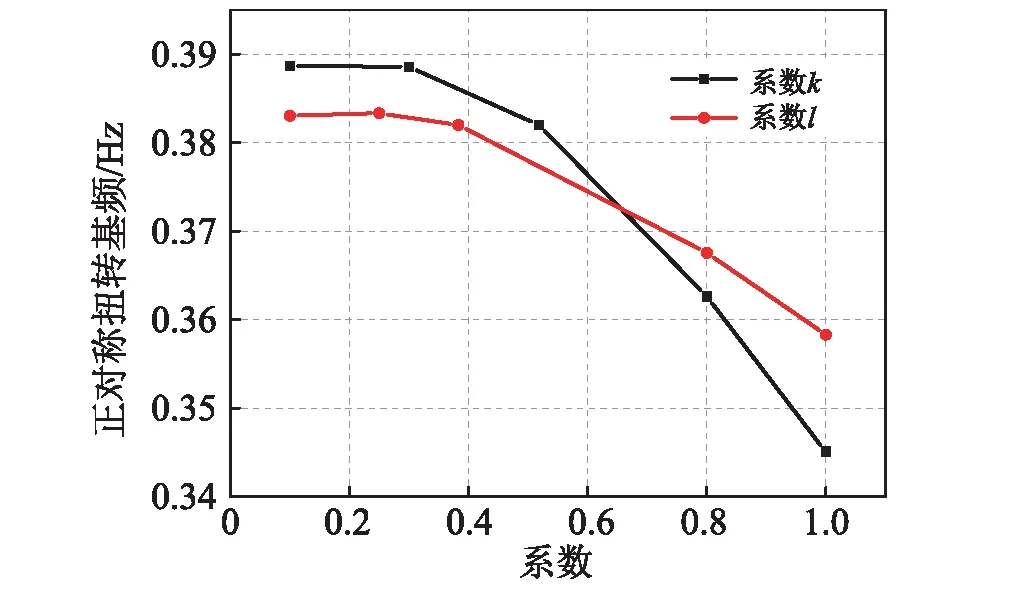
图9 系数变化对正对称扭转基频的影响Fig.9 Influence of coefficient on symmetric torsional fundamental frequency

图10 系数变化对反对称扭转基频的影响 Fig.10 Influence of coefficient on anti-symmetric torsional fundamental frequency

5 结 论

(1)推导了边跨非对称三跨连续加劲梁悬索桥正对称、反对称竖向和扭转自由振动的基频近似计算公式以及正对称下的扭弯基频比κ，并讨论了公式的适用性，非对称三跨悬索桥的跨径比例参数取极限即可得到单跨悬索桥基频估算公式，并与文献[6,8-9]中的公式进行了对比分析，表明推导的基于边跨非对称三跨连续加劲梁悬索桥基频计算公式比《公路桥梁抗风设计规范》[6]公式更具有通用性。

(2)通过某边跨非对称的三跨悬索桥算例验证了推导公式的精度，并分析了二者的误差。分别用有限元法和文中公式计算了实桥的正对称、反对称竖向弯曲自振基频和扭转自振基频，结果表明，两者的误差基本都在10%以内，文中推导的计算公式精度较高，可以在实际工程中应用。

(3)跨径相关参数变化对边跨非对称悬索桥的正对称、反对称竖弯和扭转基频有较大的影响。当跨径相关的系数k,l，其中之一保持不变，而另一个增大时，正对称、反对称竖弯和扭转的基频基本减小趋势。

(4)本文基于边跨非对称三跨连续加劲梁悬索桥推导的实用近似计算公式不仅适用于边跨非对称的双塔三跨悬索桥，而且对于快速计算简支单跨或对称三跨悬索桥的正对称、反对称竖弯和扭转自振基频，本文公式仍然适用，只是化简某些参数即可。对于主缆非对称、三塔或多塔和其他体系的基频计算公式应做专门研究。

参 考 文 献

[1] REN W X, BLANDFORD G E, HARIK I E.Finite-element model and free vibration response [J].Journal of Bridge Engineering, 2004,9(2):110-118.

[2] 韩大建,苏成,王乐文,等.香港汀九大桥动力特性研究[J].华南理工大学学报(自然科学版), 1999,27(11): 29-35.

HAN Dajian, SU Cheng, WANG Lewen, et al.A study on the dynamic behavior of the Hong Kong Ting Kau Bridge [J].Journal of South China University of Technology (Natural Science Edition), 1999, 27(11): 29-35.

[3] 张超,黄群君,许莉.考虑主塔刚度影响的三塔自锚式悬索桥竖弯频率计算公式[J].长安大学学报(自然科学版),2014,34(6):100-106.

ZHANG Chao, HUANG Qunjun ,XU Li.Frequency formulas for vertical vibration of three-tower self-anchored suspension bridge considering tower stiffness influence[J].Journal of Chang’an university (Natural Science Edition),2014,34(6):100-106.

[4] 肖汝诚.吊桥结构自振频率的计算方法[J].华东公路, 1991,2(1): 54-58.

XIAO Rucheng.The calculation method of free vibration frequency with suspension bridge[J].East Road,1991, 2(1): 54-58.

[5] 杨国俊,李子青,郝宪武,等.非对称悬索桥对称竖弯基频的实用计算公式[J].武汉大学学报(工学版), 2016,49(2): 247-253.

YANG Guojun, LI Ziqing, HAO Xianwu, et al.Practical fundamental frequency formulas for symmetric vertical vibration of asymmetry suspension bridge[J].Engineering Journal of Wuhan University,2016,49 (2): 247-253.

[6] 中华人民共和国交通部.公路桥梁抗风设计规范:JTG/T D60-01—2004 [S].北京:人民交通出版社, 2004:16-17.

[7] 刘春华,秦权.桥梁结构固有频率的统计特征[J].中国公路学报,1997,10(4): 49-54.

LIU Chunhua, QIN Quan.Statistics of natural frequencies for bridge structures[J].China Journal of Highway and Transport, 1997,10(4): 49-54.

[8] 盛善定,袁万城,范立础.悬索桥振动基频的实用估算公式[J].东北公路,1996(1): 71-76.

SHENG Shanding, YUAN Wancheng, FAN Lichu.Practical estimation formula of vibration basic frequency of suspension bridge[J].Northeast Highways,1996 ( 1): 71-76．

[9] 李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,2002: 272-275

[10] 谢官模,王超.大跨度悬索桥竖向振动基频的实用近似计算公式[J].固体力学学报, 2008,29(12): 200-203.

XIE Guanmo, WANG Chao.Approximate formula of fundamental vertical frequencies of large-span suspension bridge [J].Chinese Journal of Solid Mechanics, 2008, 29(12): 200-203.

[11] 鞠小华,廖海黎,沈锐利.对悬索桥对称竖弯基频近似公式的修正[J].土木工程学报, 2002,35(1): 44-49.

JU Xiaohua, LIAO Haili, SHEN Ruili.Modification on simplified formula of symmetric-vertical natural frequencies for suspension bridges[J].China Civil Engineering Journal, 2002,35(1):44-49.

[12] LARSEN A, GIMSING N J.Wind engineering aspects of the east bridge tender project[J].Journal of Wind Engineering & Industrial Aerodynamics, 1992, 42 (1):1405-1416.

[13] 鞠小华.三跨连续加劲梁悬索桥基频近似公式[J].铁道工程学报, 2003,78(2): 59-63.

JU Xiaohua.Approximate formulas of calculating primary frequencies for three-span continuous girder suspension bridge [J].Journal of Rail Way Engineering Society, 2003,78(2): 59-63.

[14] 焦常科,李爱群,王浩.3塔悬索桥动力特征参数分析[J].公路交通科技, 2010,27(4): 51-55.

JIAO Changke, LI Aiqun, WANG Hao.Analysis on parameters of dynamic property of triple-pylon suspension bridge [J].Journal of Highway and Transportation Research and Development, 2010,27(4): 51-55.

[15] 王本劲,马如进,陈艾荣.多塔连跨悬索桥基频估算实用公式[J].公路交通科技, 2012,29(11): 58-62.

WANG Benjin, MA Rujin, CHEN Airong.Practical formula of fundamental frequency estimation for multi-pylon suspension bridge[J].Journal of Highway and Transportation Research and Development, 2012,29(11): 58-62.

[16] 王本劲,马如进,陈艾荣.多塔连跨悬索桥基频估算方法[J].结构工程师, 2011,27(6): 54-58.

WANG Benjin, MA Rujin, CHEN Airong.Estimation of fundamental frequency of multi-pylon suspension bridges [J].Structural Engineers,2011,27 (6): 54-58.

[17] 张超.多塔自锚式悬索桥竖弯基频简化计算[J].武汉理工大学学报(交通科学与工程版), 2013,37 (4): 753-757.

ZHANG Chao.Simplified calculation of primary vertical frequencies for multi-tower self-anchored suspension bridge[J].Journal of Wuhan University of Technology(Transportation Society &Engineering), 2013,37(4): 753-757.

[18] 周勇军,张晓栋,宋一凡,等.高墩连续刚构桥纵向振动基频的能量法计算公式[J].长安大学学报(自然科学版), 2013,33(3): 48-54.

ZHOU Yongjun, ZHANG Xiaodong, SONG Yifan, et al.Calculation formula of longitude fundamental vibration frequency for continuous rigid frame bridge with higher pier based on energy method[J].Journal of Chang’an University: (Natural Science Edition), 2013,33(3): 48-54.