一种改进的认知无线电调制识别方法研究*

胡宗恺，熊 刚

（中国电子科技集团第三十研究所，四川 成都 610041）

0 引 言

近年来，随着无线通信系统的迅猛发展，人们对频谱资源和可用业务的需求不断增长。为了实现高效共享频谱并提高通信系统灵活性，认知无线电技术（Cognitive Radio，CR）越来越受到民用和军事领域的推广和重视，如宽带蜂窝通信、认知电台系统、智能电网和超宽带无线系统等[1]。美军DARPA的XG计划与SAPIENT计划明确提出了促进认知无线电在军用网络中的应用，并已经逐步实施。调制识别是认知无线电系统的一个重要组成部分，对于电磁环境感知、决策具有关键作用。根据信号调制类型，利用一些识别方法可判断区分出主用户信号与干扰信号，从而改善认知无线电系统的感知能力，利于后续的接收和解调。因此，调制识别方法有助于认知无线电系统成功实现智能通信交互。典型的调制识别思路包括两大类别：基于最大似然估计即假设检验的思路和基于统计特征的思路。后者受估计精度的影响相对较小。基于统计特征的调制识别思路一般分为信号特征提取和分类器判决两个步骤，其中分类器的设计非常重要。目前，循环谱分析、小波变换等手段已被研究人员用于一些调制识别方案，但由于受载频和符号速率估计精度的影响较大，且能够区分的信号种类有限，而对8PSK、16QAM和64QAM等较复杂调制样式的识别性能不理想，在低信噪比情况下无法进行准确判别。另一方面，对于识别分类器，有的学者研究了神经网络分类技术进行调制种类区分的方法[2-3]，如文献[2]采用了一种基于人工神经网络分类器结合循环谱分析的思路，可实现对一部分信号的调制识别分类，但是其多层分类结构计算量大，对阈值的设置也相对较为困难。

针对上述问题，本文提出了一种认知无线电调制识别新方法，计算选取优化的高阶累积量特征进行分析，具有较好的稳健性和抗噪性；在调制样式分类方面，该方法基于新型的堆叠稀疏自编码机思想（Stacked Sparse Auto-Encoder，SADE）进行分类判别，同时实现了分类器结构的改进，达到了降维的目的，进一步减少了运算复杂度，对认知无线电信号调制类型的识别性能良好。基于改进的SADE方法还能构建高质量的网络训练样本，提高了判识的精度，在低信噪比情况下可正确识别多种典型认知无线电信号调制样式，如BPSK、QPSK、8PSK、16QAM和64QAM等。

1 高阶累积量特征分析

在认知无线电通信中，常用的信号类型为数字调制方式，且调制识别是建立物理层链接的基础[4]，系统可根据发送方的调制样式等参数，判断链路建立信号并适当调整后传给接收方，然后按照回执协议反馈。

在经过下变频、滤波等预处理后，可以得到基带信号。它的采样包络为复数形式，即：

其中， ()s l表示信号的符号序列，A表示包络幅度，h(·)代表变频后剩余信道响应，T代表符号间隔，T∈代表定时误差，0f表示信号频偏，nθ表示相位偏差， ()g n表示加性高斯白噪声。实际工程中，可认为 ()x k计算求取矩的阶数有限，最大一般为8阶，且 ()g n为复数高斯随机过程。

高阶累积量作为信号处理的有效手段，能够在低信噪比条件下实现对各种调制特征的准确提取和分析，性能稳定。由于认知无线电系统授权用户信号具有非线性特征，采取高阶累积量的处理思路比较适合，且高阶累积量不仅可以降低高斯白噪声影响，而且能用于抑制非高斯噪声[5]。信号 ()x k的n阶累积量可表示为：

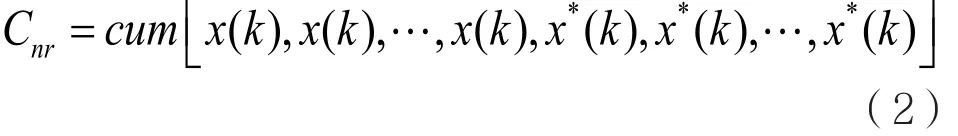
其中，阶数n也即式（2）中x(k)及其共轭x*( k ) 的总和数，r代表 x*( k ) 的数量， c um[⋅]表示累积量计算符号，且用I表示集合[x( k),x( k ) ,… ,x( k),x*( k),x*( k ) ,… ,x*( k )]， 则n阶累积量计算表达式为：

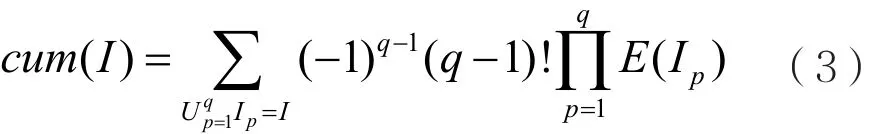
其中，表示I的子集，Ip= I 表示对I的各子集进行求和运算，且有 q ={1,2,… ,n}，p = { 1,2,… ,q }。 I p应满足UpIp=I。

采用高阶累积量提取思路，可以构造更合理的调制特征分类空间。经过计算，可得到认知无线电中典型数字调制信号类型的归一化高阶累积量，分别用 C20、 C21、 C40、 C41、 C42、 C60、C61、C62、 C63和 C80表示。表1给出了M-PSK调制和M-QAM调制信号的高阶累积量理论值。

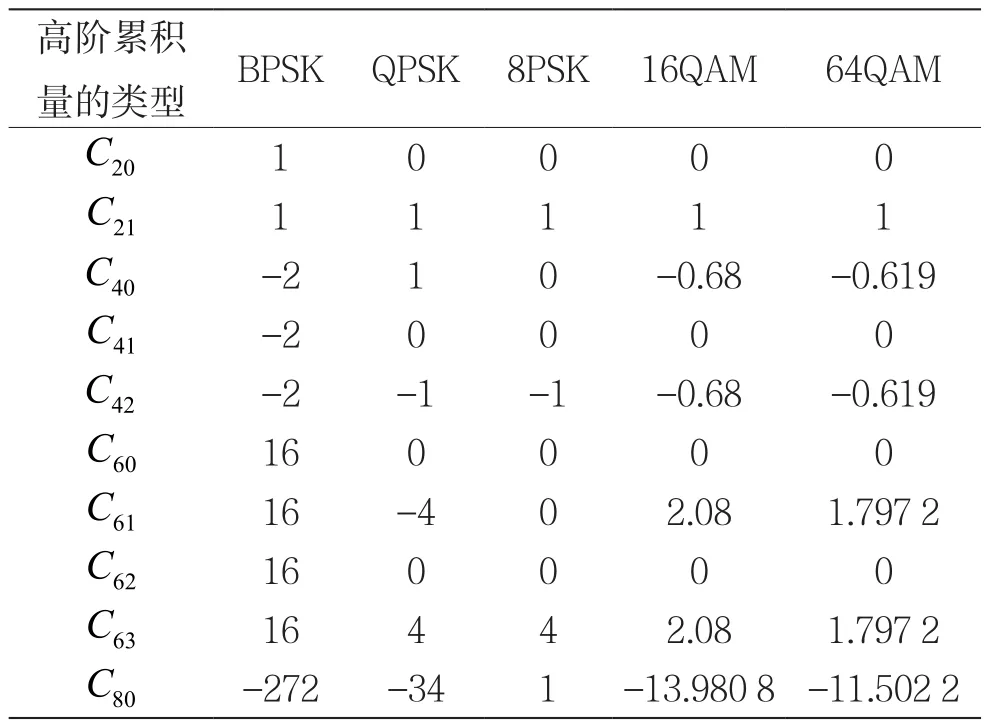
表1 M-PSK与M-QAM高阶累积量理论值列表

2 分类器算法分析及改进

堆叠稀疏自编码分类器是一种高效的深度学习模型，具有多层结构，每层的行为（输出）将被向前传送至下一层，如图1所示。其中，输入层代表输入的数组，此处输入单元的数量与输入特征数量相同。利用传统的自编码器，对于单隐含层的学习网络，可以通过计算最小代价函数获得较适合的参数，但对多层网络的情况失效[6]。因此，本文引入堆叠稀疏编码算法和降噪准则，用于包含多层的隐含层网络结构，即使其值在训练集中无法观测，仍能从加噪声的数据中重构真实样本，并通过贪婪型分层训练（Greedy Layer-wise Training）得到参数。

在分类训练过程中，自编码分类器根据学习函数将输入x转化为输出ˆ，并通过代价函数对失真进行估计，计算出各节点的优化激活。首先假设一个未标注的训练样本为 { x1,… ,xm}，定义其网络输出和代价函数分别为 hW,b(x)和 J ( W, b; x)，则该样本的代价函数计算如下：

其中W和b分别代表权系数和偏置系数。对于含有m个样本点的训练集，总代价函数的平均误差项可定义为：

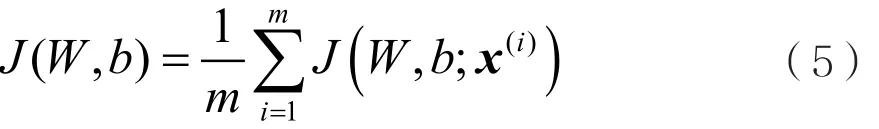
此处m表示样本数， x(i)表示输入向量。为了防止过拟合和压缩权幅值，可采用对权系数项进行衰减的方法，由此可将式（5）转化为：

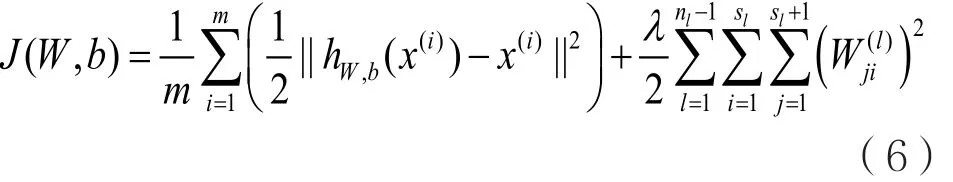
其中λ代表权重衰减参数，用以控制调节两个分量之间的相对权值，ln表示层数。

稀疏自编码器算法有一个多余约束，即当Sigmoid函数被应用其中时，大部分隐含层单元都为零值。为了将惩罚因子添加到代价函数中，首先需要引入稀疏参数ρ，通常取原点0附近的较小值，然后可得出隐含单元 j的平均活跃度，如式（7）：

其中l表示分层数，则加入代价函数后的惩罚因子项可以表示为：

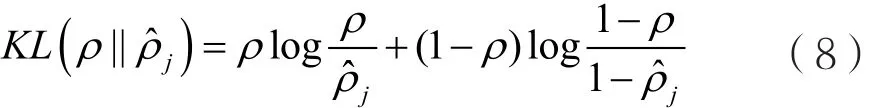
然后，引入Kullback-Leibler函数进行计算，j这是一种度量两种分布之间差异的函数。加入稀疏性惩罚因子后，新代价函数可以表示为：

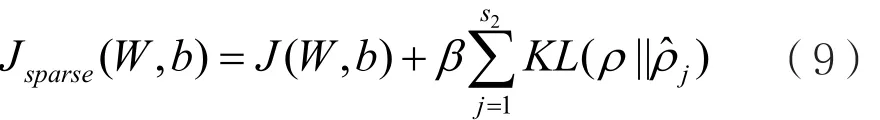
其中， s2表示隐含单元数量。为了对各层的激活进行优化， J ( W, b)应作为W和b的函数被最小化。虽然 J ( W, b)为非凸函数，在实际中梯度下降的算法思路仍可适用，定义作为激活与真实值之间的差，则为：

其中， f( z) = 1 /(1+ e xp(- z ))是sigmoid函数，)可以由式（11）给出：

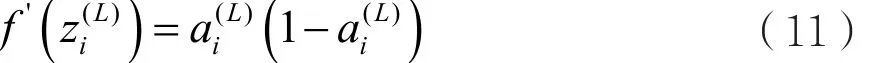
图1给出了本文中的堆叠稀疏自编码分类器的隐含层训练网络结构。

图1 堆叠稀疏自编码分类器隐含层网络结构

接下来，使用与单样本(,)x y集合相对应的偏导数方程进行计算：

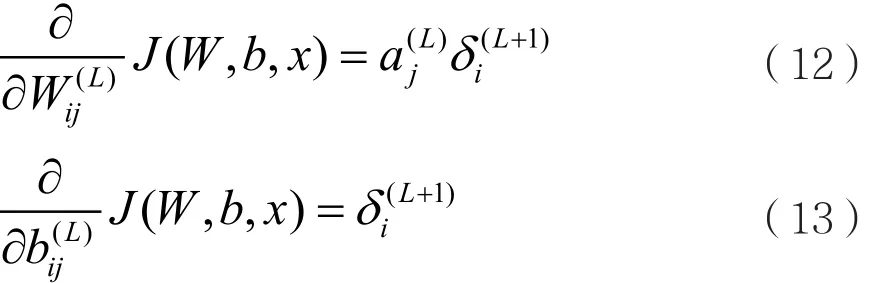
则总代价函数 (,)J W b为：

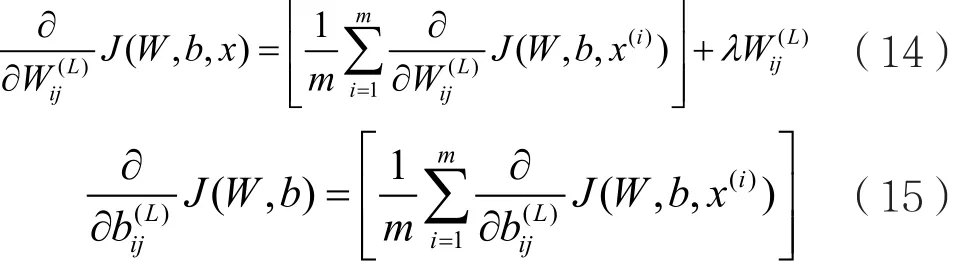
其中式（15）与式（14）不同，因为对于b而言没有权重衰减。然后，分类器训练网络中的反向传播可1通过j参数更新来实现，如：

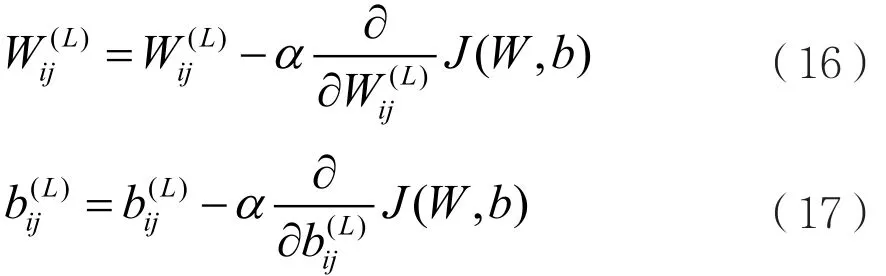
其中，α表示学习训练速度。

下面设 ΔW(l)、 ∆ b(l)分别是与 W(l)和向量 b(l)相同维数的矩阵，则分类器步骤可以表示如下：

输入——截获的认知无线电信号样本；

输出——识别分类结果（调制样式）

处理步骤：

（1）设对于各分类器层都满足 ∆ W(l)= 0 和∆ b(l)= 0 ；

（2）For i = 1:m

根据式（6）、式（10）求取偏导数，并计算：

3 仿真结果及性能分析

为了验证本文方法的有效性，采用MATLAB软件开展了以下仿真实验。仿真参数：认知无线电信号采样率为200 MHz，载波频率为20 MHz，码速率为3 Mb/s，信号采样点数为8 192，蒙特卡洛仿真次数为1 000次，噪声为加性高斯白噪声。

仿真实验1：设待分类识别的认知无线电信号调制类型为16QAM和64QAM，进行2种调制分类有效性的仿真验证，结果如图2所示。图2中不同形状的线条代表相应的信号调制类型，其中横轴表示信噪比，单位为dB，纵轴表示不同调制类型的正确分类识别率性能。

图2 本文方法的不同调制类型正确识别率曲线

仿真实验2：分别基于谱相关的识别方法、传统的基于累积量的方法和本文的改进方法进行性能比较分析，结果如图3所示。其中，横轴表示信噪比，纵轴表示正确识别率，仿真参数条件如前所述。图3中不同形状的线条代表相应的调制识别方法。

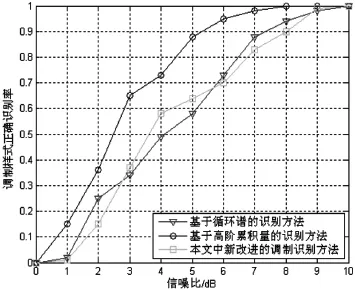
图3 各种方法的正确识别率对比曲线

从图2和图3中可以看出，本文中改进方法是一种有效的认知无线电信号识别方法，在信噪比为6 dB以上时正确识别率在95%以上，且能够有效识别高阶QAM调制。可见，新方法性能更优，且由于采用新的分类器思路，减小了运算量，比传统方法具有更好的抗噪性能和稳健型，适用于低信噪比环境中对认知无线电信号的处理。

4 结 语

随着通信技术的不断进步，认知无线电系统的应用日益广泛。在认知无线电中，信号的调制样式越来越丰富多样，电磁环境也更复杂，因此对认知无线电调制识别技术研究提出了更高需求。本文提出了一种基于高阶累积量和稀疏自编码分类器的改进方法。仿真实验表明，和一些传统方法相比，改进新方法可提高识别性能。今后还将进一步探索，为解决低信噪比环境中认知无线电调制识别问题提供一种更有效手段，并且对网电对抗领域的研究发挥重要作用。

参考文献：

[1] 白敏丹.基于认知无线电的无线通信研究现状[J].通信技术 ,2010,43(05)：45-49.BAI Min-dan.Situation of Wireless Communication research on Cognitive Radio[J].Communications Technology,2010,43(05)：45-49.

[2] Fehske A,Gaeddert J,Reed J H.A New Approach to Signal Classification Using Spectral Correlation and Neural Net-works[C].IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks,2005：144-150.

[3] Ramkumar B.Automatic Modulation Classification and Blind Equalization for Cognitive Radios[D].Virginia：Virginia Polytechnic Institute and State University,2011.

[4] Hong S,Like E,Tekin C.Multi-user Signal Classification via spectral Correlation[J].Consumer Communications and Networking Conference(CCNC),2010,7(01)：1-5.

[5] Ramkumar B,Bose T,Radenkovic M.Robust Multiuser Automatic Modulation Classifier for Multipath Fading Channels[J].New Frontiers in Dynamic Spectrum,2010 IEEE Symposium,2010,5(09)：1-10.

[6] Forero P,Canos A.Distributed Feature-based Modulation Classification Using Wireless Sensor Networks[C].Military Communications Conference,2008：1-7.