高二学生物理问题解决过程中的批判性思维水平分层研究
——基于SOLO分类评价理论
2018-05-24李晶晶潘苏东
李晶晶 潘苏东
(1. 海南师范大学物理与电子工程学院,海南 海口 571158; 2. 华东师范大学物理与材料科学学院,上海 200062;3. 华东师范大学教师教育学院,上海 200062)
1 研究目的
问题解决被列为21世纪学生必须具备的三大能力之一,问题解决的过程受到多方面因素的影响,有研究者把影响问题解决过程的内在因素分为基本能力、批判性思维和过程处理技巧3个部分.基本能力包括解决问题所需的相关领域知识及一般的策略性知识;批判性思维则在界定问题、判断相关信息、形成问题解决方案及进行反思等各个环节都扮演了重要的角色;过程处理技巧则包含论据的呈现技巧、辩论的技巧等[1].恩尼斯认为,批判性思维是问题解决过程的一个重要部分,批判性思维的5大类能力(澄清能力、获得决定所基于的信息和其他出发点相关的能力、与根据这些出发点进行推论的相关能力、元认知能力、附属能力)[2]都与问题解决有着直接的关系.
根据恩尼斯等人对批判性思维的界定,物理问题解决过程的4个阶段都离不开批判性思维的参与,从分析信息阶段到自我评价阶段,批判性思维都有参与,且对批判性思维的要求越来越高.
研究表明,批判性思维水平不会简单地随着年龄的增长而提高,但却可以通过学习得到提升.[3]如果学生没有付出努力,他的高阶思维水平就不会得到提高,批判性思维作为高阶思维的一种,同样需要经历一定难度的练习后才能得到提高,在物理教学中可以利用问题解决来提升学生的批判性思维水平.研究中学生在物理问题解决过程中的批判性思维发展水平对于提高学生物理问题解决能力有着特殊的作用.本研究拟基于SOLO分类评价理论对学生在解决物理问题过程中的批判性思维发展水平进行研究.
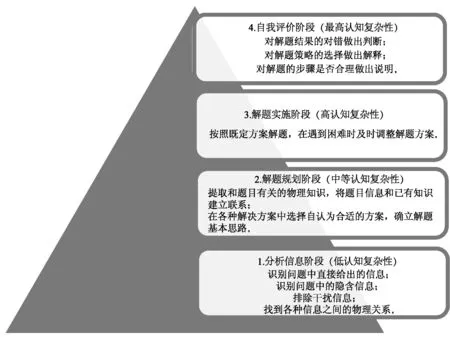
图1 物理问题解决过程中批判性思维参与层级表
SOLO是英文“Structure of the Observed Learning Outcome”首字母的缩写,意为“观察到的学习结果的结构”,是澳大利亚著名教育心理学家比格斯(Biggs)和他的同事科利斯(Collis)提出的,他们认为,一个人的总体认知结构是不可测量的,但其在解决某个具体问题时所表现出来的思维结构是可测量的,而且表现出的思维水平可以从低到高划分为5个层次: 前结构(基本无法理解和解决问题)、单点结构(对问题略知一二,但无法解决)、多点结构(对问题有了更多的了解,但不全面)、关联结构(对问题有整体把握,并能解决问题)和抽象拓展结构(能对问题进行抽象概括,并应用于新的情境).“我们可以判断学生在回答某一具体问题时的思维结构处于哪一层次,关注学生在特定任务上的表现.这种分析学生解决一个问题时所达到的思维高度的评价方法就称为SOLO分类评价”.[4]
2 研究设计
2.1 研究假设
本研究假设高二学生在解决物理问题的过程中表现出的批判性思维能力水平是不同的,并呈现为由低到高的连续体.
2.2 研究方法
研究主要采用质性研究的方法,通过现场采集学生在物理问题解决过程中的解题步骤、想法等相关信息,进行整理,以SOLO分类评价理论为参照,根据不同学生的表现提炼出学生在物理问题解决过程中批判性思维的等级水平.
2.3 选择被试
在海口市属重点高中随机选取一个高二年级普通班,根据皮亚杰的认知发展阶段论和对批判性思维的研究,初中生的批判性思维水平尚浅,很难对其进行有效地分层,高一学生刚刚入校,和初中生差异不明显,选择高二年级学生进行研究是比较理想的.因为是质性研究,很难进行大样本调查,选择市属重点高中普通班主要考虑到这个样本群体比较能够代表普通偏高学生的一般水平.所选班级共53人,其中男生31人,女生22人,平均年龄在18岁左右.
2.4 数据采集
给定测试题目,要求学生作答,在作答的过程保留原始做题痕迹(做错后用笔在上面轻轻画线,不要直接涂改),解答完毕后根据学生答题情况对部分学生进行针对性访谈,了解学生做题过程中的真实想法.
测试题目:一列火车由机车牵引沿水平轨道行驶,经过时间t,其速度由0增大到v.已知列车总质量为M,机车功率P保持不变,列车所受阻力f为恒力.求:这段时间内列车通过的路程.
选择这个题目是因为学生对这类题目并不陌生,任何层次的学生应该都能参与解题,同时,解决问题所需要的公式也比较简单,避免复杂运算带来的其他干扰.
3 研究结果
根据SOLO分类评价理论对学生问题解决过程中思维水平的分层及物理问题解决过程中批判性思维参与层级表,经过对学生的答题痕迹和访谈录音进行分析,我们认为可以把高二学生在物理问题解决过程中的批判性思维表现水平分为4个层次.
3.1 第1层次(LCT-1)
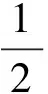
可以看出,这部分学生虽然能够表述出题目中给出的具体信息,但他们却无法找到隐藏的关键信息,题目中机车在0到t时刻内,功率保持不变,而机车速度在增大,意味着牵引力在减小,因此,机车在这段时间内并非做匀变速运动,匀变速直线运动的公式和高中所学的牛顿第二定律的公式在这里都是不适用的.在交流中发现,这部分学生并没有能够分析出机车的运动状态,他们仅仅是把题目中的表面信息和头脑中的公式进行了简单匹配,没有对信息进行进一步的深入思考,判断它们之间的物理关系.而且,有学生表示,除了用匀变速运动公式,他们没有别的方法把题目所求的位移与运动速度及运动时间等联系起来.这说明,这部分学生缺少解决这个物理问题所需的知识,由于知识储备不足,导致他们在解决这个问题时无法列举不同的解决方案,更无从选择最优方案.访谈结果显示,这部分学生对自己的解题方案并没有明确的规划,能写多少公式就写多少,至于对错,他们并不清楚,完全不具备对解题过程和解题结果的评估能力.
以上分析可知,这部分学生基本不具备物理解题所需的批判性思维能力,我们将这种表现定义为第1层次,用LCT-1(Level of Critical Thinking-1)来表示,对应SOLO分类评价中的前结构层次,这个层次的学生在求解物理问题时主要表现为:无法对题目中给出的信息进行有效的判断,建立它们之间的物理关系;无法结合已有知识进行解题规划;对解题过程中需要用到的概念、规律、物理思想等解释不清楚、不准确,导致在解题过程中遇到困难;缺乏对问题解决方案的评估能力.
3.2 第2层次(LCT-2)
在学生的答卷中,我们发现有两种错误的解法.
错解1:以列车为研究对象,水平方向受牵引力和阻力f.据P=Fv可知,牵引力为
由F-f=Ma可求得
求得
错解2:以列车为研究对象,水平方向受牵引力和阻力f.据P=Fv可知,牵引力为
根据动能定理有
求得
这两种错解看似不同,但却有着相似之处,错误的根源都是没能根据题目中告知的机车功率不变,推导出机车牵引力并非恒力.和单点层次结构类似,虽然学生并没有直接跳到答案,但学生对自己选择的解决问题方案缺少分析,在不清楚方案对错的情况下盲目使用,导致答案错误.在对使用错解1学生的访谈中发现,与第1层次的学生不同,这些学生对使用牛顿第二定律解决动力学问题有着一定的经验,能够进行解题规划.“这个题目一看就知道是动力学问题,告诉了时间,速度,受力情况,求位移.……这种题目我们原来做过很多,只要用牛顿第二定律加上匀变速运动公式,肯定就能算出来.”这意味着这部分学生可以快速地找到题目中给出的物体受力、运动时间、速度变化等信息,并能有意识地将这些信息建立起联系.但他们并没有对题目中的信息仔细地进行分析和解释,辨别是否可以使用匀变速运动公式进行求解.当被要求对自己的解题方法和解答过程进行正误判断时,只有两位学生醒悟过来,“好像不对,v增大,F就减小了,不是匀加速,做错了.”其他同学大多认为“应该没问题吧!”使用错解2的学生选择了用动能定理解题,表现出了更加丰富的知识储备,在访谈中发现,他们认为这类题目通常有两种解法,一种是用动力学公式求解,一种就是用动能定理求解.至于为什么选择动能定理,我们得到了不同的回答,有学生认为动能定理计算简单,省掉了中间过程;有学生表示没有多想,因为老师强调过能用动能定理就不用动力学方程.可以看出,这部分学生对动力学和动能定理都有一定的理解,能够将头脑题目中的信息和这些知识进行链接,但由于对学科知识缺少深层次的理解,他们往往不能在各种解决问题的方案中进行正确的选择,同样,也无法对自己选择方案的正误进行判断.
与第1层次的学生相比,这部分学生具备一点物理解题所需的批判性思维能力,我们将这种表现定义为第2层次,用LCT-2来表示,对应SOLO分类评价中的单点结构层次.他们能够对题目中给出的信息进行判断,并找到各类信息之间的物理关系;具有一定的物理知识储备,并能提取相关的解题经验,但缺乏对学科知识的深层次理解和对隐含信息的提取和分析能力,导致无法进行正确的解题规划;很难对解题步骤和结果进行正确评价.
3.3 第3层次(LCT-3)
我们发现使用错解2(19人)的学生比使用错解1的学生(3人)要多,在对使用错解2的部分学生进行访谈时,有3个学生比较典型,他们对选择使用动能定理的理由是“机车功率不变,但是速度变大了,所以F就变小了,所以机车不是做匀变速直线运动,……那就只能用动能定理了.”当我们试图提醒“你已经知道了机车所受的牵引力并非恒力,那你觉得你的解题过程有问题吗?”学生很肯定地告知“没有问题,因为动能定理在任何条件下都适用,不是恒力做功也可以用.”显然,这几名学生已经掌握了动力学解决物理问题的方法,甚至对动力学解决问题的局限性也有所了解,对动能定理的内涵也有一定的理解,但却在在求解做功的问题上未曾考虑到变力做功的求法.表面来看,学生只是一时大意,但根据其对解题过程的评价可以看出,学生缺乏对整个问题解决过程的逻辑思考,选择解题策略时关注到的隐藏信息在进行具体解题方法选择时被彻底抛弃了,这意味着学生尚没有能力对问题进行全面的分析.而在对自己的解题过程进行审查时,学生并没有意识到自己的错误,说明他尚未掌握自我检查的方法,仅仅对部分关键条件进行了反思,而忽略了对解题整体规划合理性的检查.
与处于LCT-2阶段的学生相比,这几名学生对学科知识的理解显然更加深刻一些,他们很清楚地知道利用动力学公式和动能定理可以解决哪些类型的问题,并能根据题目信息判断出机车所做的是非匀变速直线运动,从而选择用动能定理解题.但由于缺乏对问题的整体把控,他们最终并没能够选择正确的解题方案.我们将其表现定义为第3层次,用LCT-3来表示,对应SOLO分类评价中的多点结构层次.这个层次学生的表现是:能够分清题目给出的各种信息,并能够利用已有的解决问题经验对问题进行归类;学生在表达可以用于解决问题的前提知识(定义/定理/数据)时,精确而清晰,能够制定解决问题的方案;但缺乏对解决问题的整体规划,缺乏对前后关系的逻辑判断,从而导致无法找到问题的最佳解决方案;在对解题步骤和结果进行评价时缺乏判断.
3.4 第4层次(LCT-4)
全班大概有二分之一的学生给出了正确的解答过程,在和这部分学生交流的过程中我们发现,他们读取信息和进行解题计划的能力都比前几个层次的学生更胜一筹.这部分学生能够很快地将题目中给出的信息进行整理,结合原有解题经验进行分析,判断出此题只能用动能定理求解.“题目中说明了机车功率不变,但是速度在变大,所以F会变小.这类变力做功问题通常会用到动能定理,题目求的是位移,那就更是用动能定理了——合外力做功等于动能的改变量,位移和做功有关.”学生对选择用动能定理解题并不是盲目的,他们是在将题目所给信息和所求物理量进行了认真分析之后做出的决定.在分析的过程中,学生发现此题中的机车并非做匀变速运动,因此他们在求做功的问题上并没有使用W=Fs这个常见公式,而是选择了W=Pt.
这种表现与SOLO模型中定义的第4层次关联结构层次对应,我们将其定义为第4层次,用LCT-4来表示.这部分学生的表现是:能够分清题目给出的各种信息,并能够利用已有的解决问题经验对问题进行归类;学生在表达可以用于解决问题的前提知识(定义/定理/数据)时,精确而清晰,最终能够根据所提供的事实,前提知识,明确的程序,制定解决问题的方案,并且逻辑非常清晰;对解题过程中的每一步都能非常清楚和详细地进行描述,并能建立起相应的物理模型;以清晰、精确、相关和深刻的方式解决问题;在对解题步骤和结果进行评价时能够做到有根有据,逻辑清楚.
SOLO模型中定义的最高思维层次是抽象拓展层次,表现为能对问题进行抽象概括,从而做到举一反三.这种应用迁移能力无法从答卷中看出,但在随后的访谈中我们发现,能够给出此题正确解答的学生基本都能对这类问题的解决过程进行总结和反思,明确这类问题的解决方案.当然,这和任课教师曾经在课堂上强调过此类问题的解决方法有很大关联.单从学生在解决此问题的表现上看,基本能够达到关联结构层次的学生也都达到了抽象拓展层次.
4 结论
调查结果说明高二学生在解决物理问题中的批判性思维水平是不一致的,可以根据他们的不同表现分为由低到高的4个层次,这和我们的研究假设基本吻合.
关于学生解决物理问题过程中的批判性思维分层结果可概括如下: (1) 无法在解决问题时使用批判性思维的学生(LCTA-1):只能识别给定的事实和问题,但不能和头脑中已有信息发生联系以进行更深层次的分析; (2) 在解决问题过程中批判性思维技能较弱的学生(LCTA-2):可以识别事实和问题,能够和已有知识(概念/定理/数据)进行联系,但在制定问题解决方案的过程中缺乏对相关信息的判断和思考,缺乏自我反思的能力; (3) 在解决问题过程中具有一定批判性思维技能的学生(LCTA-3):可以识别事实和问题,可以根据给定信息激活头脑中已有的相关图式,进行解题规划,并能对自己解决问题的过程有一个大致的判断; (4) 在解决问题过程中批判性思维技能较强的学生(LCTA-4):可以清楚地识别提供的各种信息,迅速激活相关图式,进行正确的解题规划,对自己的解题步骤和结果能进行有根据的判断和评价.
由于样本和所选题目的限制,在此次研究中发现处于第1层级和第3层级的学生人数都非常有限,学生基本集中在第2层级和第4层级,这个结论是否可以推广还有待进一步的研究.
参考文献:
1 Cindy L. Lynch and Susan K. Wolcott WolcottLynch Associates. Helping Your Students Develop Critical Thinking Skills[J]. Journal of College Teaching & Learning,2015(2):101-108.
2 武宏志,张志敏,武晓蓓. 批判性思维初探[M]. 北京:中国社会科学出版社,2015:61.
3 戴维·希契柯克, 张亦凡, 周文慧. 批判性思维教育理念[J]. 高等教育研究, 2012(11):54-63.
4 Biggs J,Collis K. Evaluating the Quality of Learning——SOLO Taxonomy.New york:Academic Press,1982:13-15.
