基于网络数据预测电影票房的多元线性回归方程构建

何晓雪 毕圆梦 姜绳

摘 要 随着经济实力的不断增长和人民生活水平的日益提高，我国电影市场得到了蓬勃发展，对国民经济的贡献率不断上升。对电影票房进行科学的预测，不仅能够对电影本身的投资有所帮助，同时也可以促进电影产业进行科学合理的资源配置。文章利用多元线性回归方程，通过采集近年来的电影票房数据样本，从豆瓣评分、微博想看人数、M1905电影网的相关新闻数量及电影首映日票房等多个角度构建了票房预测模型，并确定了最终影响实际票房的三大因素，最后构建了电影的票房预测模型并得出了预测票房结论。

关键词 多元线性回归方程；电影；票房预测

中图分类号 G2 文献标识码 A 文章编号 2096-0360（2018）05-0041-08

1 研究背景

随着我国经济实力不断增长，人民生活水平日益提高，消费能力也在逐步提升。人们更加重视对美好生活的追求，其尤为突出的一个侧面便是休闲娱乐投资所占比例越来越大。特别是近些年来，我国电影市场蓬勃发展，围观中提供了无数银幕佳作，人们的观影热情也随之越发高涨，又进一步推动了电影市场对经济贡献率的不断上升。这种相互递进的经济效应，使得人们对于新生电影能否带来理想票房愈发重视。

2017年，著名导演冯小刚的新片《芳华》宣布退出国庆黄金档，无疑掀起一阵巨浪，更激起我们对于其撤档背后是否与票房密切相关这一点产生了长久的思考。为研究此问题，需要一个合适的票房预测模型。2013年Google发布了一篇名为《Quantifying， movie magic with Google Search》的论文，里面提出一種基于多元线性回归方程的电影票房预测模型，通过其能在电影上映前1个月得到该电影的首周票房，并且预测成功率高达94%。由于一部电影涉及众多环节，其票房的影响因素也纷繁复杂，而且程度有大有小，不同类型电影可以考察的参数亦不同。

1.1 多元线性回归方程预测票房的可行性

多元线性回归方程正是考虑到多方因素作用来计算的一种常用数学模型。它可以采用多个变量组合来预估某一变量，较单一变量预测更符合实际，误差更小，结果更有效，具有广泛的适用性，更符合现代社会的实际情况，而且实现简单，易于人们理解和操作。因此，我们决定沿用这一模型对电影《芳华》票房进行预测分析，进而为电影行业的发展产生一些实际借鉴意义。

1.2 国内外研究历史及经验

随着互联网时代的高速发展，网民在线生成人数爆炸式增长，信息交互传递的速度越来越快。2006年，Gilad Mishne和Natalie Glance通过分析博客中有关电影的数据，构建了基于博客的电影票房预测模型，研究关于电影的口碑声量和口碑的情感分析对票房的影响程度，最终揭示了口碑声量的影响力更大。2010年，itaram Asur和Bernardo A.Huberman通过实验得到了在推特中的电影声量与票房呈线性相关，并且其数据的正负情感分析对票房也有很大影响的结论。在2013年，Chong Oh等利用推特里关于电影的口碑数据和boxofficemojo.com的电影票房数据分析，得出口碑能直接影响电影票房的结论，而且观影用户反馈及片方的前期推广信息也间接影响整体的票房成绩。

2 研究过程

2.1 影响电影票房的因素猜测

根据前人的研究与实验成果，我们可以看出，用户口碑、关注度以及新闻宣传对电影票房有积极影响。自商品经济发展以来，口碑便是极为重要的影响因素。而在社交媒体盛行的当下，海量数据的挖掘无疑要从这一领域开始。其中，微博，作为一种通过关注机制分享简短实时信息的广播式的社交网络平台，截至2016年，月平均活跃人数达到2.97亿。庞大的用户覆盖面使其在新闻舆论、综艺娱乐等方面继续保持绝对影响力，而对于电影行业的发展推动力也不容小觑。知名大V，各种营销号的前期推广，即时性的用户反馈与信息传递，无时无刻不在影响着一部电影的票房走势。豆瓣，作为老牌书影音交流社区，凭借优质的用户评论和较为客观的电影评分，也成为我们本次研究的数据参考之一。此外，我们还选取了电影网站的新闻数据，进一步思考前期宣传与票房的关系，综合探究口碑这一宏观概念对于票房方面的影响。

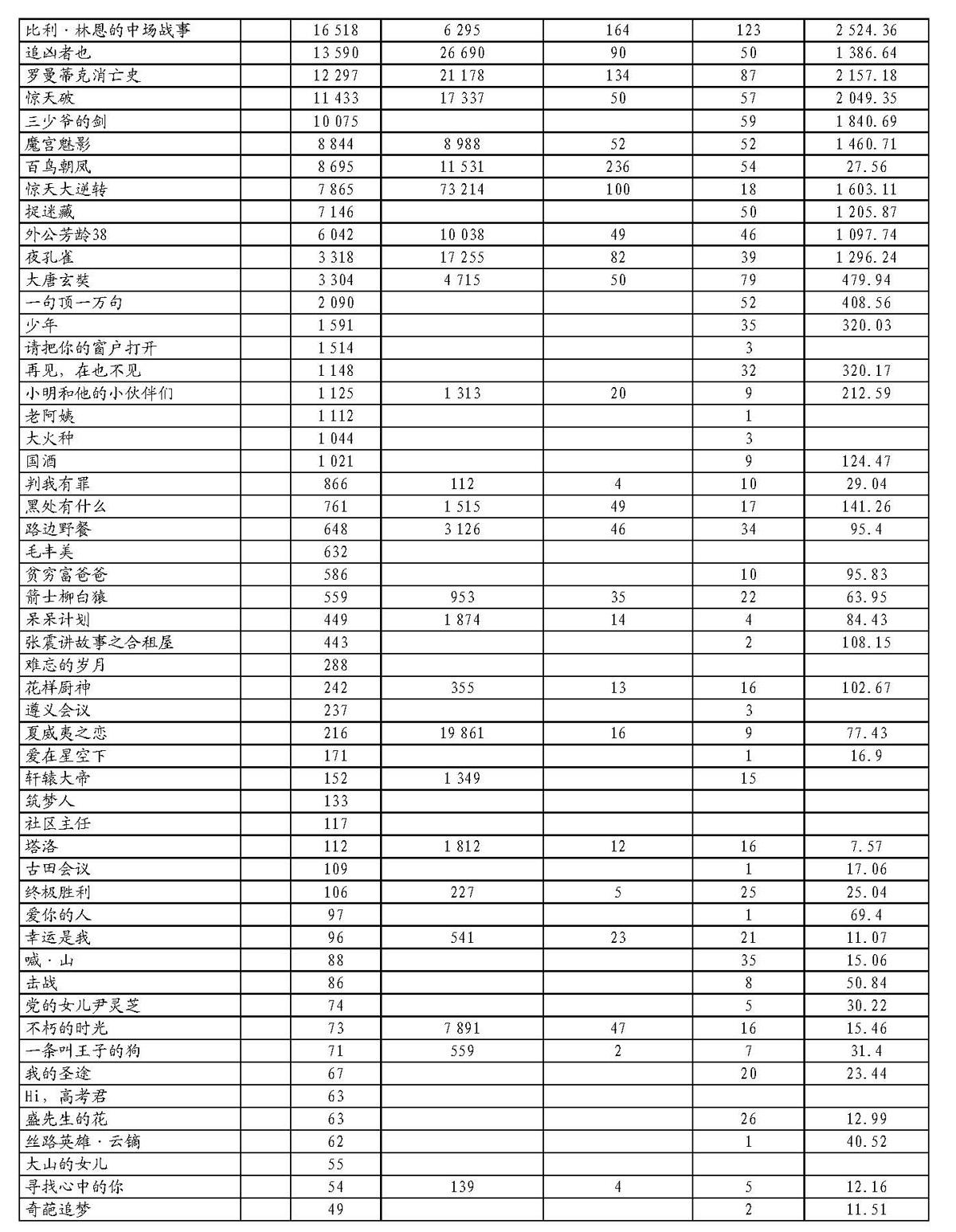
在这些数据中，口碑数量与产品营销成正相关关系。同时，电影票房也是自相关的，前期宣传力度大、关注度高、近期票房高的电影总票房就会比较高。因此，我们分别针对豆瓣评分、微博中表示“想看”某部电影的人数、M1905电影网相关资讯及首映日票房与电影总票房的关系进行了研究探索。表1为搜集的近年电影样本数据表，表2为数据采集来源表。

2.2 影像电影票房因素的确定方法

上文提到“豆瓣评分”、微博表示“想看”人数、M1905电影网相关影视新闻和电影首映日票房与电影实际票房的情况看起来似乎都有极大的关系。为了验证这4个因素是否有关系，有什么样的关系，我们采用单个元素分析，最后整合的方式进行试探。

第一，分别将上述元素作为唯一自变量，将两年内所找到的电影实际票房作为因变量，分别利用SPSS统计软件进行线性回归探索。在线性回归探索中，如果R2的数值越接近1，那么这个与票房的关系越紧密。

第二，再对自变量、因变量进行显著性分析，在得出的结果中看显著性。显著性的临界值是0.05，即超过这个值，因变量与自变量的线性关系无法建立，应当舍弃。

第三，对于符合上述两个条件的自变量与因变量关系再此进行验证，并用软件自动建立线性回归公式。这个公式暂时不具有参考意义，只是对于自变量与因变量关系的存在进行证明。

第四，当确定与实际票房有线性关系的因素后，将这些因素全部作为自变量，将实际票房作为因变量，再次利用SPSS软件，重复上述三个步骤，建立多元线性回归方程，这个方程就是所得的票房预测方程。

第五，利用所得方程，将电影《芳华》的自变量数据带入，经计算得出最终结论。

2.3 猜测因素与票房关系探索

2.3.1 豆瓣评分与票房关系探索

基于之前的假设，首先对豆瓣评分与实际票房之间的关系做分析。通过运用SPSS统计软件，将表1中2017年芳华类电影的豆瓣评分作为自变量，实际票房作为因变量输入软件，进行了线性回归分析，探索二者之间的关系。结果如表3所示。

在这个表中，R2的数值是0.083，远远小于1，这表示电影实际票房的8.3%可由豆瓣评分来解释。鉴于在R?的值越接近1，其拟合效果越好的这个规律，可以初步判定豆瓣评分与电影实际票房之间的关系不大。为了确定这个结论，再将豆瓣评分与票房关系显著性进行分析，结果如表4所示。

在显著性分析中，当结果值大于0.05时说明模型受误差因素干扰太大不能接受。由表4可以看出，这里的显著性为0.115，远远超过了0.05，也就是由自变量“豆瓣评分”和因变量“电影实际票房”建立的线性关系回归模型没有显著的统计学意义。所以再次证明，豆瓣评分不能作为我们预测电影票房的依据。

2.3.2 微博表示“想看”电影人数与电影实际票房关系探索

与探索豆瓣评分与票房关系的方法相同，将2016年和2017年芳华类电影的微博“想看”人数作为自变量，实际票房数据作为因变量，进行了线性回归分析，结果如表5所示。

在表格中，可以R?是0.424，大于可作为参考因素的临界值0.3，表示电影票房的42.5%可以通过电影的微博“想看”人数来解释，所以微博“想看”人数是可以作为我们预测电影票房的一个重要依据的。同样，再次进行微博“想看”人数与票房关系显著性分析，以验证上述猜想，结果如表6、表7所示。

这里得到了结果的显著性为0.000，因为精确值的关系，软件并未显示具体数值，但可以明确看出这个数值远小于临界值0.05，这表明由自变量“电影的微博‘想看人数”和因变量“电影实际票房”建立的线性回归模型具有极显著的统计学意义。

为了确定微博“想看”人数与票房关系的线性关系，我们再次将二者通过SPSS软件进行显著性分析，并试图得出结论。如表7所示。

從系数这一栏中我们可以得到建模的直接结果，并且系数的显著性也是0.000，说明该线性回归方程是有意义的。根据软件所给结论，某电影微博“想看”人数（X）与电影实际票房（Y）的模型表达式为：Y=0.598X+2 418.659。

2.3.3 M1905电影网相关影视新闻数量与电影实际票房的关系探索

M1905电影网也是一个十分具有影响力的网站。在这个网站中，我们主要选择2016年和2017年芳华类电影在M1905上的新闻资讯的数量和实际票房，用同样的方法进行了线性回归分析，结果如表8

所示。

我们看到R2是0.461，说明电影票房的46.1%可以用M1905的新闻资讯数量解释。

再对M1905相关影视新闻数量与票房关系显著性进行分析，结果如表9、表10所示。

显著性为0.000，根据前面的经验，这里的实际数值应当是小于0.01的一个值，远小于0.05，表明由自变量“M1905的相关新闻资讯数量”和因变量“电影实际票房”建立的线性回归模型具有极显著的统计学意义。

再次对M1905电影网相关影视新闻数量与票房关系进行线性方程的建立。分析结果如表10。

从系数这一栏中我们可以得到建模的直接结果，所以M1905的相关新闻数量与电影实际票房的模型表达式为：Y=402.470X-3732.455。

2.3.4 电影首映日票房与电影实际票房的关系

探索

探讨电影首映日票房与实际票房的关系，我们同样用2016年和2017年芳华类电影的首映日票房和实际票房的数值进行了线性回归分析，分析结果如表11所示。

我们看到R?是0.575，表示电影票房的57.5%可以通过电影的首映日票房来解释，所以电影的首映日票房应当是预测电影票房的一个重要依据。再对电影首映日票房与实际票房关系进行显著性分析，结果如表12、表13所示。

从这个结果中，我们可以看到，显著性为0.000，应当是小于0.01中的某个值，远小于0.05，表明由自变量“电影的首映日票房”和因变量“电影实际票房”建立的线性回归模型具有极显著的统计学意义。

从系数这一栏中我们可以得到建模的直接结果，所以电影首映日票房与电影实际票房的模型表达式为：Y=8.841X-76.196。

2.4 多元线性回归方程的确定

基于前面的分析，可以确定最终一个电影在其微博上表示“想看”人数、电影首映日票房以及M1905电影网网站上电影相关新闻的数量有着线性关系。把这三个作为自变量，电影实际票房作为因变量构建多元线性回归模型，进行可行性探索，结果如表14所示。

在这个表中，我们看到R?是0.675，表示电影票房的67.5%可以通过这三个变量来解释，也就是说我们预测模型的准确率在67.5%左右。继续分析三要素与电影实际票房关系显著性。结果如表15、表16所示。

在表15中，我们看到，自变量与因变量关系的显著性为0.000，即小于0.01的某个值，远小于0.05，表明由这三个自变量和因变量“电影实际票房”建立的多元线性回归模型具有极显著的统计学意义。

在表16中，非标准化系数作为自变量的系数，常量作为线性回归公式的常量，可以取得最后的线性回归公式：

Y=0.275X1+4.447X2+204.055X3-6 082.328

其中：X1=某电影微博表示“想看”的人数，X2=电影首映日票房，X3=M1905电影网相关影视新闻报道量。

3 《芳华》电影预测

根据上述公式，我们找到了截至2018年3月5日，电影《芳华》的微博“想看”人数为42 505，首映日票房为7 579.25万，M1905新闻网网站上关于电影《芳华》的新闻数量为159，把数据代入方程中，我们预测出的电影《芳华》实际票房为11 688.875+33 704.925+32 444.745-6 082.328=71 756.217（万元），即7.2亿。

4 模型总结与讨论

根据中国网的报道，截至2018年1月2日，电影《芳华》的票房就已经超过12.7亿①，远大于我们所预测的票房数。这样的大误差说明我们的预测结果不能够正确地预测《芳华》的票房。那么，这个模型是否能够有效测出电影实际票房，我们对2017年的电影数据选取了10部进行了抽样分析②，得出结果如表17所示。

在这个表中，我们看到，偏差率尽管通过SPSS进行统计出的线性回归公式并未准确地预测出《芳华》的票房，但是通过验证，我们所得的多元线性回归方程基本能够满足预测票房的要求。当然，我们也知道，这个公式还有它的局限性，也希望读者进行批评指正。

注释

①资料来源：芳华1月2日累计票房超12.7亿 芳华挺进华语电影票房前十，万家热线网.http：//365jia.cn/news/2018-01-03/DC8C64355BD5C349.html.

②数据测试电影选取方法：表1中的前十部电影。因为表1中的每一部电影之间没有直接的关联，所以直接选取这个表格中的前十部，可以认定为随机抽取。

③数据更新截止到2018年3月5日。

参考文献

[1]郑坚，周尚波.基于神经网络的电影票房预测建模[J].计算机应用，2014，34（3）：742-748.

[2]任丹.基于多元线性回归模型的电影票房预测系统设计与实现[D].广州：中山大学软件工程学院，2015.

作者简介：何晓雪，上海外国语大学新闻传播学院学生。

毕圆梦，上海外国语大学新闻传播学院学生。

姜 绳，上海外国语大学国际关系与公共事务学院博士生。