Dirac Quasinormal Modes of Static f(R)de Sitter Black Holes∗

Hong Ma(马洪)

Department of Physics,Chongqing University,Chongqing 401331,China

1 Introduction

The universe is con fi rmed by plenty of observations to be in a period of accelerated expansion.[1−7]Many scientists have proposed a variety of models to explain the accelerating expansion,including thef(R)gravity theory.[8−11]As a nonlinear theory of gravity modifying the General Relativity(GR)with an additional scalar field,f(R)gravity has attracted much attention and has been considered as a candidate to explain the accelerated expansion.[12]Furthermore,recent four gravitational waves(GWs)events from the merger of binary BHs have been detected by Advanced LIGO,[13−16]where QNMs also appears.Later,it indicates that the recent experimental precision possibly satisfies the requirement of testing modi fi ed theories of gravity.[15]Accordingly,as an explanation of the phenomenon of cosmic acceleration,f(R)theory might be demonstrated by GWs observation,which has a considerable realistic signi fi cance.

f(R)BHs are investigated by constant scalar curvaturethe cosmological constant can be assigned tof(R)gravity).[17]The key point of the study includes two kinds off(R)BHs:One isf(R)BH imposed by constant scalar curvature withdenoting the Schwarzschild de Sitter(dS),Schwarzschild Anti de Sitter(AdS)and Schwarzschild BHs respectively,[18−19]which can be deduced by redefining the Newtonian constant.These BHs are calledf(R)(Schwarzschild)BHs,[18−19]which are deduced fromf(R)gravity.Another is obtained byf(R)gravity coupled to the matterwhere the matter fields are the Maxwell[20]and Yang-Mills fields[21](Since the Yang-Mills fields only give it a relatively complex approximate numerical expressions,I do not discuss here).I consider thef(R)(Maxwell)BHs withandandR0=0 denoting the Reissner-Nordström-de Sitter(RNdS),Reissner-Nordström-anti de Sitter(RNAdS)and Reissner-Nordström(RN)BHs,which may lead to these BHs by redefining Newtonian constant and charge.[21]Thesef(R)BHs are shown in Table 1(lists of line element includingf(R)BHs and classic BHs).

In the cause of seeking physical characteristics off(R)BHs,we should perturb these spacetimes and study the QNMs generated by the perturbation.QNMs ringing produces complex frequency.The oscillation rate is described by the real component and the damping rate is symbolized by the imaginary part.Yun Soo Myung investigated stability off(R)(Schwarzschild)BH[19]and gave a perturbations master equation of gravitational vector field,which is consistent with the gravitational field perturbations in the Schwarzschild BH given by Wheeler.[24]Taeyoon moon studied the thermodynamic properties off(R)(Maxwell)BH.Except as the geometry of the BH,properties of QNMs spectrums also rely on the nature of the perturbation field,such as spin.Hence,scalar,electromagnetic,and gravitational perturbations of QNMs were researched in large quantities.[25−28]Cho has investigated Dirac QNMs in Schwarzschild BHs.[29]Sub-sequently,Dirac perturbations in the regular spacetimes were analyzed by Liet al.[30]In order to make the research of Dirac QNMs more comprehensive,therefore,the focus of research in this paper is analyzing the QNMs of Dirac perturbations in thef(R)spacetimes.

So far,Chandrasekhar and Detweiler[31]firstly applied calculation method to the QNMs of BHs.Then Schutz and Will propose darray WKB approximation method,[32−38]to solve the low-frequency attenuation QNMs. Leaver proposed the continued fraction method.[39]However,in this article,I will focus on howf(R)BHs are quietly affected by the correction factorR0changes.The stability of thef(R)BHs is analyzed by the finite difference method.Meanwhile,I choose one ofR0from reasonable range,and use the WKB approximation method to reveal QNMs of thef(R)dS spacetimes under Dirac perturbation in massless and massive case.

The paper is organized as follows.Dirac perturbations of QNMs are brie fl y reviewed by Sec.2.The stability of thef(R)BHs is analyzed by the finite difference method in Sec.3.The QNMs are numerically calculated using the WKB method in Sec.4,including two parts:Subsec.4.1,QNMs for massless fields are evaluated.Subsec.4.2,the QNMs for massive case are analyzed.The crucial results and prospects are described in Sec.5.

Table 1 It shows a summary of f(R)BHs and classical BHs.Speci fi c details about f(R)BHs can be obtained in Refs.[19–23].

2 Dirac Perturbation in the f(R)Spacetime

Dirac field equation with massmin the spacetime of BHs can be expressed as[40−41]

There are two different kinds of spin magnetic quantum numbers.Hence,wave functions must be defined separately.[30]I suppose

IntroducingMaking some changes inF±andG±as,[40]

I choosej=l−1/2 to the analysis of the QNMs,which is identical withj=l+1/2.In addition,the Dirac particle has the same QNMs with the antiparticle in the spherically symmetricf(R)BHs.In such spacetimes,the radial functionˆF−stands for all relevant physics of the evolution of the Dirac field.

3 Stability Analysis off(R)BHs by the Finite difference Method

Finite difference Method is a method with numerical simulation in the earliest use of computer,[42]and it is still widely used.The basic idea is using a finite number of grid composed with discrete points instead of the contiguous area of definite solution,and these discrete points are called grid node.[43]By using Taylor expansion and so on,continuous definite area on continuous variable of function is used for the grid defined on a discrete variable function as a valid approximation process,and the integration is also replaced by the integral sum.This is a common numerical approximate solution,and it has been applied to many fields.[44]Finite difference method can not only be employed to asymptotically flat spacetimes,but also can be applied to the studying of QNMs in AdS spacetime.We use reasonable differential mode in order to obtain figures of discrete type and waveform.Therefore,the dynamic evolution of thef(R)BHs is analyzed by the finite difference method.Furthermore,the stability off(R)BHs is analyzed only in the dS spacetime.Equation(15)can be expressed as

differential equations forF±(µ,ν)andG±(µ,ν)are given by Eq.(28)in this transformation,which can be integrated by the finite difference method.[45]

Figure 1 illuminates the structure off(R)(Schwarzschild)BHs andf(R)(Maxwell)BHs in dS spacetime.The spacetime becomes more curved with the increase ofR0.Furthermore,Fig.2 describes that the potential functions vary with different values ofR0inf(R)spacetime.The structure of various modes in Fig.1 is consistent with each situation in Fig.2.From Fig.2(a)the potential increases with the increase ofR0.From Fig.2(b),the peak of the potential barrier grows with enhancingR0.

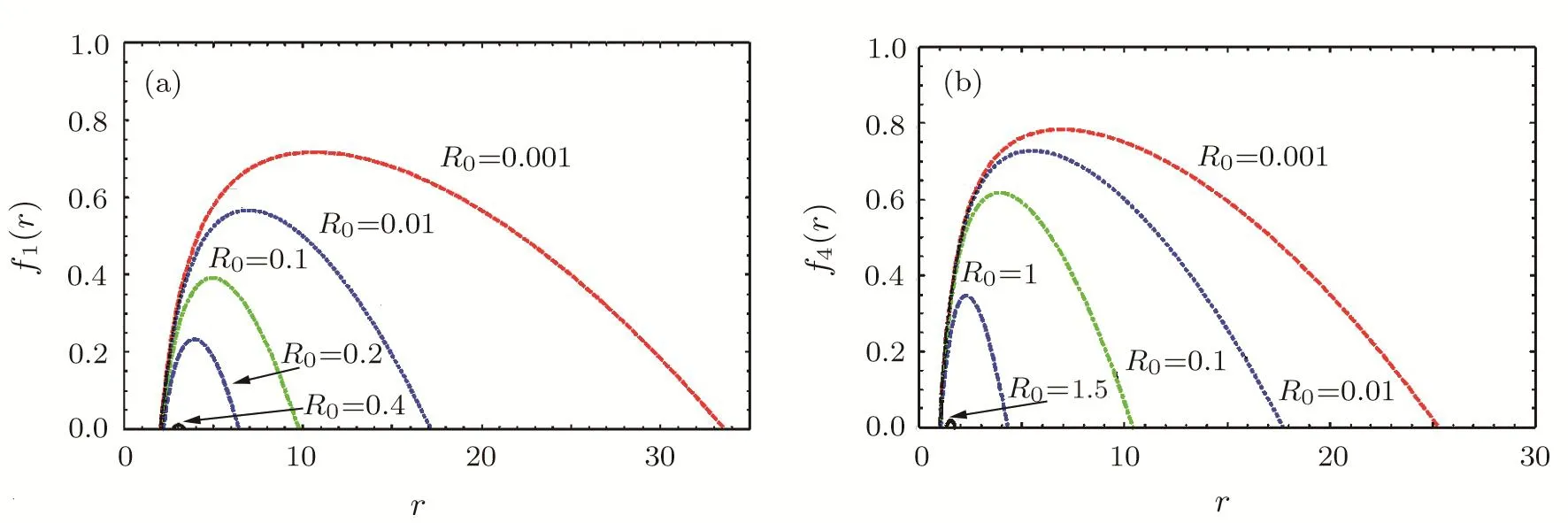
Fig.1 The structures of the f(R)BH’s metric function f(r)with different values of R0:(a)Show f(R)(Schwarzschild)BHs spacetimes with M =1,|k|=1 and r+=1(from top to bottom:R0=0.001,0.01,0.1,0.2,0.4).(b)Show f(R)(Maxwell)BHs spacetimes with M=1,|k|=1,r+=1,Q=0.1 and f′(R0)= −0.1(from top to bottom:R0=0.001,0.01,0.1,1,1.5).

Fig.2 The effective potential of Dirac perturbations in f(R)spacetime with different values of R0:(a)Show f(R)(Schwarzschild)BHs spacetimes with M=1,|k|=1 and r+=1(from top to bottom:R0=0.001,0.01,0.1,0.2,0.4).(b)Show f(R)(Maxwell)BHs spacetimes with M=1,|k|=1,r+=1,Q=0.1 and f′(R0)= −0.1(from top to bottom:R0=0.001,0.01,0.1,1,1.5).

The QNMs frequencies of the Dirac perturbation forf(R)(schwarzschild)BHs andf(R)(Maxwell)BHs are calculated by fi nite difference method.Figure 3 shows the dynamics evolution of each mode,whereMis mass off(R)BHs,|k|is the related to angular quantum number values.ωis the QNMs frequency.R0is the value of the correction factor.Here I concentrate on the effects of different values ofR0on thef(R)BHs.Figure 3 describes the evolution of the Dirac field inf(R)(schwarzschild)BH andf(R)(Maxwell)BH.The decay rate|Im(ω)|decreases with increasingR0and oscillation rate Re(ω)enhances.Moreover,Fig.3(a)illuminates that|Im(ω)|off(R)(schwarzschild)BH is slower than that of Schwarzschild BH(R0=0),and the oscillation frequency Re(ω)becomes tighter than Schwarzschild BH(R0=0).Similarly,Fig.3(b)shows that the same property off(R)(Maxwell)BHs about the e ff ect ofR0on BHs.

Another point worth noting is that the presence ofR0would in fl uence on QNMs off(R)BHs.From Fig.3,it can be found that with the increase ofR0in the tail of the image tends to be flat.With further increase ofR0,the time duration off(R)BH becomes shorter and shorter.UntilR0=0.4 in Fig.3(a)shows the stage of QNMs almost disappears inf(R)(schwarzschild)spacetime,meanwhile,whenR0=1.5 in Fig.3(b)the stage of QNMs almost disappears inf(R)(Maxwell)spacetime.The results show that,with the increase ofR0the oscillation becomes more quickly and damping becomes more slowly.

In addition,Fig.3 can be considered as the dynamic evolution of the uncharged and chargedf(R)BHs withR0in the dS spacetimes.whenR0=0.001 the BH will experience stable process after perturbation andf(R)BHs are at a critical state.Therefore,the massless and massive Dirac fields are calculated by the WKB method whenR0=0.001,in order to distinguish thef(R)BHs and classics BHs of QNMs.

From Fig.4(a),Re(ω)increases with increasing|k|whileR0=0.001,and|Im(ω)|decreases slowly with increasing|k|.The results show that the oscillation off(R)(Schwarzschild)BHs becomes more quickly and the damping speed decreases slowly.Meanwhile,Fig.4(b)showsf(R)(Maxwell)BH off′(R0)=−1 andR0=0.001(RNdS),and the increase of|k|.The oscillation of the chargedf(R)BHs becomes more fast and the damping speed slowly decreases.

Fig.3 The dynamical evolution of Dirac perturbations to the f(R)black hole varying with R0:(a)Show f(R)(Schwarzschild)BHs with M=1,|k|=1 and r+=1(from top to bottom:R0=0.4,0.2,0.1,0.01,0.001,0).(b)Show f(R)(Maxwell)BHs with M=1,|k|=1,r+=1,Q=0.1 and f′(R0)= −0.1(from top to bottom:R0=1.5,1,0.1,0.01,0.001,0).

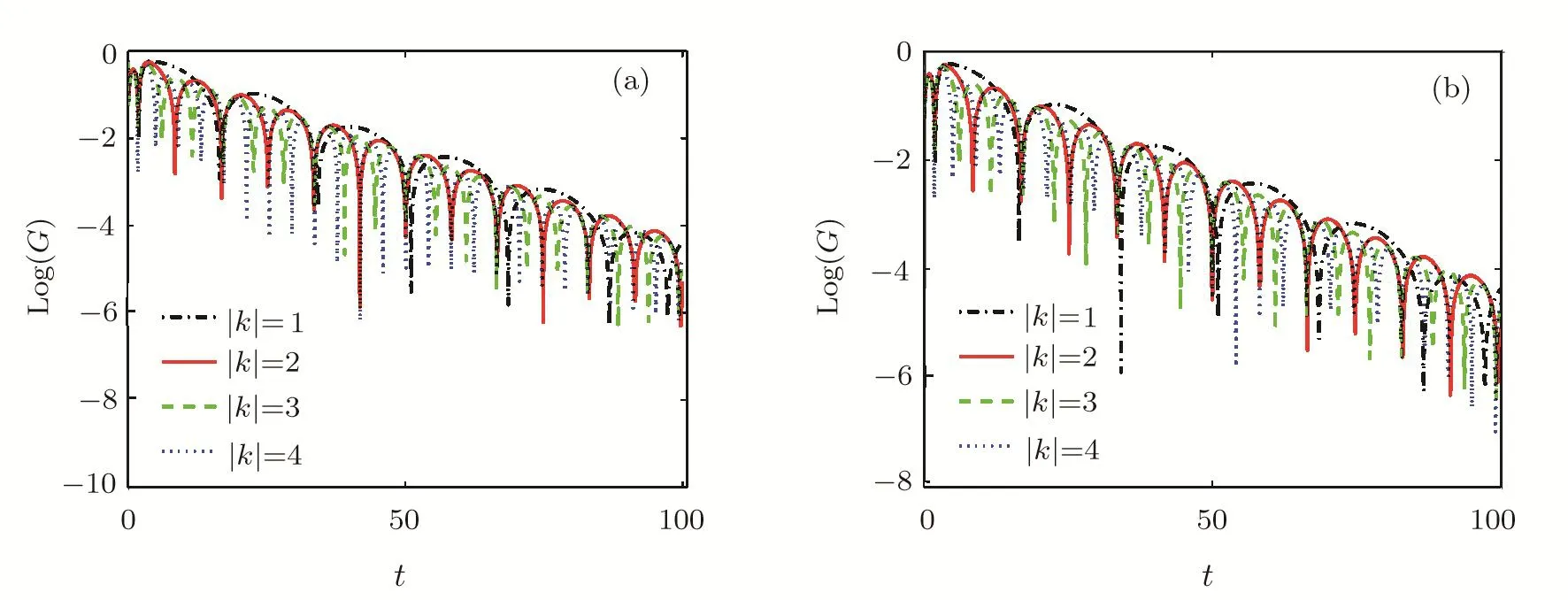
Fig.4 The dynamical evolution of f(R)black holes with various|k|.Here the Dot Dashed,the Line,the Dashed,the Dotted correspond to|k|=1,2,3,4.

4 The QNMs Frequency Calculated by WKB Approximation Method

4.1 QNMs for the Massless Dirac Field

From the one-dimensional Schrödinger Eqs.(18)and(19),the QNMs frequencies can be calculated by the WKB approximation method.In Eqs.(20)and(21)are the super-potentials.Obviously,the QNMs frequency of the corresponding potential energy is the same.I employ the potential equivalent of Eq.(21)to calculate the QNMs.is used as an example

The“−”subscripts and superscripts for the remainder section are dropped by simplifying the notation.I also setr+=1.

It is noteworthy that the tortoise coordinates requests that the spacetimes of event horizon tend to be flat in the in fi nite area.Therefore,thef(R)BHs QNMs frequencies in the de sitter spacetimes are calculated by the WKB method.So I chooseR0=0.001 to calculatef(R)(Schwarzschild)black hole’s QNMs and chooseto calculatef(R)(Maxwell)black hole’s QNMs in de sitter spacetime.

The effective potential function emerges as a barrier.Figure 5 illuminateds the potential functions outside the event horizon.Figure 5(a)shows the effective potential function of thef(R)(Schwarzschild)BH whenR0=0.001.The peak of the potential barrier enhances with increasing|k|,and the peak position shifts to the left.Similarly,Fig.5(b)shows that the same property off(R)(Maxwell)BHs about the effective potential.

The QNMs frequencies of Schwarzschild BHs,f(R)(Schwarzschild)BHs,Reissner-Nordström BHs andf(R)(Maxwell)BHs with|k|=1,2,3 are analyzed by the WKB method.The QNMs frequencies off(R)black holes are compared with classic black hole in Tables 2 and 3.Assumingr+=1,I calculate the QNM frequency whenn=0 andn=1.The results are shown that Re(ω)tends to increase with enhancing|k|,but|Im(ω)|tends to decrease whilen=0 andn=1.In addition,Table 4 shows that given|k|,Re(ω)and|Im(ω)|both enhance slowly with increasing the chargeQ.It indicates that the chargeQimpacts on the damping of QNMs.Compared with Reissner-Nordström BH,f(R)(Maxwell)BH also has the same properties.Furthermore,from Table 5,oscillation frequency Re(ω)and decay frequency|Im(ω)|both decrease with the enhancement ofR0.This results are consistent with our results obtained by fi nite difference method.It means that it will a ff ect the stability off(R)BH with the increase ofR0.

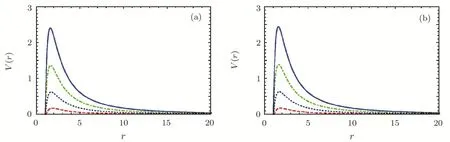
Fig.5 The effective potential of Dirac perturbations in f(R)spacetime with different values of R0:(a)Show f(R)(Schwarzschild)BHs spacetimes with M=1,R0=0.001 and r+=1(from top to bottom:|k|=4,3,2,1).(b)Show f(R)(Maxwell)BHs spacetimes with M=1,R0=0.001,r+=1,Q=0.1 and f′(R0)= −0.1(from top to bottom:|k|=4,3,2,1).

Table 2 WKB Approach of f3(r)and f1(r)(M=1,R0=0.001,and r+=1).

Table 3 WKB Approach of f6(r)and f4(r)(M=1,f′(R0)= −0.1,R0=0.001,Q=0.1,and r+=1)

Table 4 WKB Approach of f6(r)and f4(r)(M=1,f′(R0)= −0.1,R0=0.001,|k|=1,and r+=1)

Table 5 QNMs frequencies of f1(r)and f4(r)via WKB method

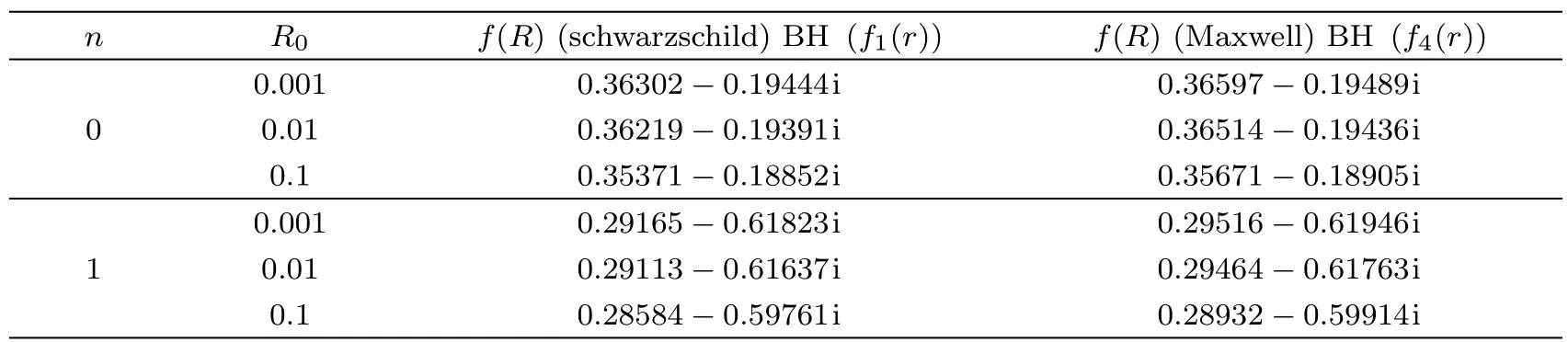
Table 5 QNMs frequencies of f1(r)and f4(r)via WKB method

?

4.2 QNMs for the Massive Dirac Field

The Dirac QNMs of massivef(R)black holes are calculated by the third-order WKB method.So the effective potential functionsV(r)rely onm.This makes the calculation much more complicated.From Fig.6 the peak potential enhances with the increase ofm.Nevertheless,whenpotential energy will approach asymptotically tom2.As form

On theonehand,Tables6and 7show the Schwarzschild BH andf(R)(Schwarzschild)BH QNMs frequencies.When|k|is fixed,Re(ω)decreases with the increase ofm,but|Im(ω)|increases with the increase ofm.It means that when the field with massive particles increases,the oscillation becomes slower,but the decay goes faster.On the other hand,I also calculate the QNMs of Reissner-Nordström BH andf(R)(Maxwell)BH.From the Tables 8 and 9,I obtain the same result as the case of Schwarzschild BH andf(R)(Schwarzschild)BH.I can also find that when the massmincreases,Re(ω)of the frequency decreases and|Im(ω)|of the frequency increases.It indicates that the QNMs frequency oscillation becomes slow and the decay becomes fast.A possible explanation is that the massive particles are absorbed by BH when the disturbance occurs,so disturbances in the form of a BH would take away as the energy of gravitational waves.Furthermore,oscillation rate Re(ω)enhances but decay rate|Im(ω)|becomes slow with the increase of|k|.

Fig.6 (a)f(R)(Schwarzschild)black hole with R0=0.001(from top to bottom:m=0.9,0.7,0.5,0.3,0.1);(b)f(R)(Maxwell)back hole with R0=0.001,f′(R0)= −0.1,and Q=0.1(from top to bottom m=0.9,0.7,0.5,0.3,0.1).Variation in the effective potential for Dirac perturbation fields in static f(R)spacetime.I set n=0,|k|=1,M=1.

Table 6 ω in Schwarzschild BH(f3(r))given by 3-order WKB approach(r+=1,M=1).

Table 7 ω in f(R)(Schwarzschild)BH(f1(r))given by 3-order WKB approach(r+=1,M=1,R0=0.001).

Table 8 ω in Reissner-Nordström BH(f6(r))given by 3-order WKB approach(r+=1,M=1,Q=0.1).

Table 9 ω in f(R)(Maxwell)BH(f4(r))given by 3-order WKB approach(r+=1,M=1,R0=0.001,f′(R0)= −0.1,Q=0.1).

5 Conclusion

Here I have performed a detailed analysis of Dirac quasinormal spectrum of asymptotically dS BHs inf(R)theory of four dimensions.Thef(R)theory is a modi fication to the gravitation theory.WhenR0=0,thef(R)(Schwarzschild)BH will come back to the Schwarzschild BH.WhenR0=0 and 1+f′(R0)>0,thef(R)(Maxwell)BH is similar to Reissner-Nordström BH.Therefore,I focus on nonzeroR0correction factor.Here the dynamic evolution of thef(R)BHs is studied by the fi nite difference method,and the QNMs of Dirac perturbation forf(R)BHs are solved by third-order WKB method.

The results of this paper are summarized:

(i)With the fi nite difference method,oscillation frequency Re(ω)enhances and decay rate|Im(ω)|decreases with increasingR0.It is worth noting that,the tail off(R)BHs tends to be flat with increasingR0.With the further increase ofR0,the duration of QNMs oscillation becomes shorter and shorter.I comparef(R)BHs with classic BHs(R0=0).It indicates that theR0has a great in fl uence on the stability.In addition,with increase of|k|,the oscillation frequency Re(ω)enhances but decay rate|Im(ω)|decreases slowly.

(ii)With third-order WKB method,the results give some important comparisons off(R)BHs and the corresponding classical BHs,which can reveal how thef(R)theory impacts on the QNMs of the BHs.In the massless case, firstly,I comparef(R)(Schwarzschild)BH and Schwarzschild BH.I find that the oscillation frequency Re(ω)increases with the increase of|k|but decay rate|Im(ω)|decreases slowly.Secondly,I comparef(R)(Maxwell)BH and Reissner-Nordström BH,and I find that givenQ,oscillation frequency Re(ω)enhances with increasing|k|while decay rate|Im(ω)|decreases.I also analyze the impact ofR0on the QNMs of thef(R)BHs.Re(ω)and|Im(ω)|both decrease with the enhancement ofR0.This is consistent with the result of the fi nite difference method.

(iii)In the massive case,the effective potential functionsV(r)rely onm.The peak of potential function enhances with largerm.I find that given|k|with increasingm,Re(ω)decreases and|Im(ω)|enhances.It means that the heavier the field particle,the slower oscillation it has,but the decay goes faster.It can be explained as that,in the massive Dirac field,perturbations of black holes would keep a longer time.Concerning increase of|k|,it will cause more energy taken away in the form of waves and resulting in faster oscillation and decay.

There are some problems and further researchs in the future work.Firstly,I should take more accurate calculation methods to calculate QNMs in the more general case.Moreover,I should broaden the focus on the study associated with the high-frequency part and fully study physical nature inside.Secondly,I should also concern high-dimensional spacetimes,the existing research only involves a few simple models,and then some other types off(R)gravity theories also can be considered for the topics of disturbance of the Dirac particles.These interesting perspectives can be undertaken as subsequent research studies in the near future.

[1]S.Perlmutter,et al.,Astrophys.J.517(1999)565.

[2]A.G.Riess,et al.,Astrophys.J.116(1998)1009.

[3]A.G.Riess,et al.,Astrophys.J.607(2004)665.

[4]A.Grant,et al.,Astrophys.J.560(2001)49.

[5]S.Perlmutter,M.S.Turner,and M.White,Phys.Rev.Lett.83(1999)670.

[6]C.L.Bennett,et al.,Astrophys.J.Suppl.Ser.148(2003)1.

[7]G.Hinshaw,et al.,Astrophys.J.Suppl.Ser.148(2003)135.

[8]J.Geom,Meth.Mod.Phys.4(2007)115.

[9]S.Capozziello,M.De Laurentis,and V.Faraoni,arXiv:0909.4672[gr-qc].

[10]T.P.Sotiriou and V.Faraoni,Rev.Mod.Phys.82(2010)451.

[11]S.Nojiri and S.D.Odintsov,Phys.Rept.59(2011)144.

[12]S.Perlmutter,G.Aldering,et al.,Nature 391(1998)51.

[13]B.P.Abbott,R.Abbott,T.D.Abbott,et al.,Phys.Rev.Lett.116(2016)061102.

[14]B.P.Abbott,R.Abbott,T.D.Abbott,et al.,Phys.Rev.Lett.116(2016)241103.

[15]B.P.Abbott,R.Abbott,T.D.Abbott,et al.,Phys.Rev.Lett.116(2016)221101.

[16]B.P.Abbott,R.Abbott,T.D.Abbott,et al.,Phys.Rev.Lett.119(2017)141101.

[17]A.De la Cruz-Dombriz and A.Dobado,Phys.Rev.D 74(2006)087501.

[18]G.Cognola,E.Elizalde,S.Nojiri,S.D.Odintsov,and S.Zerbini,J.Cosmol.Astropart.Phys.0502(2005)010.

[19]Y.S.Myung,T.Moon,and E.J.Son,Phys.Rev.D 83(2011)124009.

[20]A.De la Cruz-Dombriz,A.Dobado,and A.L.Maroto,Phys.Rev.D 83(2011)029903(E).

[21]Taeyoon.Moona,Myungb.Yun Soo,and Edwin J.Son,Gen.Relativ.G 43(2011)3079.

[22]T.Moon,Y.S.Myung,and E.J.Son,Eur.Phys.J.C 71(2011)1.

[23]A.De la Cruz-Dombriz,A.Dobado,and A.L.Maroto,Phys.Rev.D 80(2009)124011.

[24]T.Regge and J.A.Wheeler,Phys.Rev.108(1957)1063.

[25]K.A.Bronnikov,R.A.Konoplya,and A.Zhidenko,Phys.Rev.D 86(2012)024028.

[26]A.Flachi and J.P.S.Lemos,Phys.Rev.D 87(2013)024034.

[27]Kai Lin,Jin Li,and Nan Yang,Gen.Relativ.Gravit.43(2011)1889.

[28]M.Hong and L.Jin,Chin.Phys.B 26(2017)060400.

[29]H.T.Cho,Phys.Rev.D 68(2003)024003.

[30]Jin Li,Hong Ma,and Kai Lin,Phys.Rev.D 88(2013)064001.

[31]S.Chandrasekhar and S.Detweiler,Proc.R.Soc.London,Ser.A 344(1975)1634.

[32]B.F.Sehutz and C.M.Will,Astrophys.J.291(1985)33.

[33]S.Iyer and C.M.Will,Phys.Rev.D 35(1987)3621.

[34]S.Iyer,Phys.Rev.D 41(1990)3632.

[35]K.D.Kokkotas and B.F.Sehutz,Phys.Rev.D 37(1988)3378.

[36]E.Seidel and S.Iyer,Phys.Rev.D 41(1990)374.

[37]K.D.Kokkotas,Nuovo Cimento B 108(1993)991.

[38]R.A.Konoplya,Phys.Rev.D 68(2003)024018.

[39]E.W.Leaver,Proc.R.Soc.A 402(1985)285.

[40]D.R.Brill and J.A.Wheeler,Rev.Mod.Phys.29(1957)465.

[41]H.T.Cho,Phys.Rev.D 73(2006)024019.

[42]C.Gundlach,R.H.Price,and J.Pullin,Phys.Rev.D 49(1994)883.

[43]C.Gundlach,R.H.Price,and J.Pullin,Phys.Rev.D 49(1994)890.

[44]X.He,B.Wang,and S.B.Chen,Phys.Rev.D 79(2009)084005.

[45]Jin Li and Y.H.Zhong,Int.J.Theor.Phys.52(2013)1583.