Parameterization of Nuclear Hulthén Potential for Nucleus-Nucleus Elastic Scattering
2018-05-23BhoiUpadhyayandLaha
J.Bhoi, R.Upadhyay, and U.Laha
1Department of Physics,Government College of Engineering,Kalahandi-766002,Odisha,India
2Department of Physics,National Institute of Technology,Jamshedpur-831014,India
1 Introduction
Theα-αandα-3He systems have been studied quite extensively by a number of groups.[1−16]These studies provide a large number of data.Besides experiments,several phenomenological interaction models have also been proposed for theα-αandα-3He systems[17−30]which produce more or less similar results although their way of approaches to the problems are different.Thus,one can easily rely on these data.The basic purposes of theααscattering experiments are to gather information about the nature ofα-αinteraction and also to investigate the energy levels of8Be[16,26−29,31−34]through the study of resonance behavior of phase shifts.8Be,being an unstable system,can easily be dissolved into twoαparticles and is a typical example of a system of twoα-particles.Similarly,7Li is regarded as two clusters of nucleons namely anα-particle and a triton.In such model the effective interaction,considered between each pair of particles,is a fi nite depth central potential.Since theα-particles are tightly bound,the low lying states of such systems can be determined fairly well through the relative motion of theα-particle only.One of the interesting features of theα-αscattering is to see whether,resonances corresponding to the low energy states in8Be are observed or not.The general procedure to understand it is to make use of the partial wave analysis of the phase shiftsδlfor a given partial wave with angular momentuml.Since the spin ofαparticle is zero and possess high internal binding energy,so the phase shifts can easily be reduced to a minimum and one can able to analyze the scattering in terms of real phase shifts up to a laboratory bombarding energy of 35 MeV.Theα-αandα-3He elastic scattering have also been studied quite extensively by a number of groups.[35−42]Mohr[42]has treated the low energyα-3He elastic scattering within the framework of a simple two-body model together with a double-folding potential.In the recent past,Ne ff[43]studied the radiative capture cross sections for theα-3He andα-3H reactions using a two-body effective interaction together with microscopic fermionic molecular dynamics approach to the problem.
Theα-α,α-3He orα-3H interaction is a combination of the Coulomb potential and a short range interaction.The short range interaction is of nuclear origin while the Coulomb potential takes care of the charges.We propose here a two-term four parameter nuclear Hulthén[30,44]type potential for the short range part and the atomic Hulthén one for the electromagnetic interaction.Based on the phase function method(PFM)for local potentials[45]we shall compute the elastic scattering phase shifts for the systems under consideration and judge the merit of our proposed model.The present article is an effort in this direction.In Sec.2 we propose our interaction model and brie fl y outline the PFM.Section 3 is devoted to results and discussion.Finally,we conclude in Sec.4.
2 Interaction Model and the PFM
In the phenomenological approach one generally attempts to construct an interaction which reproduces the standard values of the low energy scattering parameters and the phase shifts for a particular system.Assuming8Be a 2αsystem Haefner[18]in 1951 proposed anα-αpotential which is repulsive for smallrand attractive for intermediater.Later,with a modi fi ed Haefner interaction,Nilsonet al.[19]were able to reproduce theα-αscattering phase shifts in the energy range 0 to 22 MeV.In 1958 Van der Spuy and Pienaar[20]made a phenomenological analysis of theα-αscattering up to a bombarding energy of 6 MeV by considering a potential with three parameter namely:the hard core radius,the nuclear interaction range and the well depth.Further,in 1964 Endo,Shimodaya and Hiura[22]investigated theα-αscattering with an energy independent butl-dependent potential with an attractive and a repulsive part.They obtained a good fi t to phase shifts up toELab=50 MeV for lower partial waves.Later on several potentials have also been proposed by a number of authors to study the systems involving light nuclei.
In 1977 Buck,Friedrich and Wheatley[25]proposed a two-parameter angular momentum and energyindependent local Gaussian potential of the form
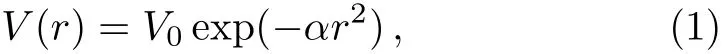
withV0=−122.6225 MeV andα=0.22 fm−2.They were able to reproduce the scattering phase shifts up toELab=80 MeV together with the binding energy and resonance width of the ground state of8Be.Marquez[27]successfully described theα-αsystem by considering a Woods-Saxon type potential for the nuclear part of the form

The above potential involves four adjustable parametersVw,Aw,Rw,andRcto reproduce the energy and decay width of the8Be ground state as well as the phase shifts for the partial waves up tol=6.Subsequently,in 1984 it was proved[26]that the Potential of Bucket al.[25]and the one proposed by Marquez[27]are identical.In the meantime,several sophisticated potential models for the light nuclei systems have also been proposed.[16,31−33,43]
In the recent past we have studied the alpha-nucleon systems within the formalism of supersymmetric quantum mechanics and alpha-nucleus systems by representing the short range interaction with a two-parameter nuclear Hulthén potential.[30,44]Our two-term four parameter nuclear Hulthén interaction reads as

withV0,the strength anda,the screening radius of the atomic Hulthén potential. In the limit,the potential in Eq.(5)goes over to Coulomb potential ifV0a2=e2=1 in atomic unit,au=5.291 772×10−11m).In the un-screening limit i.e.andV0→0 such that their product remains a constantaV0=2kη,whereηis the Sommerfeld parameter.[44]In atomic and plasma physics screened and cut-o ffCoulomb potentials are important.Many standard results in non-relativistic scattering theory for the short-range potentials have to be modi fi ed for charged particle scattering as the particles interacting via the Coulomb potential never behave like free particles.Even the asymptotic condition for a well behaved potential does not hold and as a consequence the concept of a phase shift is ill defined for Coulomb scattering.To that end an exponentially screened Coulomb potential,the atomic Hulthn one,is considered for the electromagnetic part.It has been used frequently in dynamical calculations because it is explicitly soluble.[45]HereVE(r)is a short range potential and can be dealt with within the framework of traditional phase function method.
The phase function method represents an efficient approach to evaluate the scattering phase shifts for quantum mechanical problems involving local[46]and non-local interactions.[47−50]In this case the radial wave function of the Schrödinger equation is separated into an amplitude part and an oscillating part with a variable phaseδl(k,r).For a local potentialδl(k,r)satisfies a first order nonlinear differential equation given by
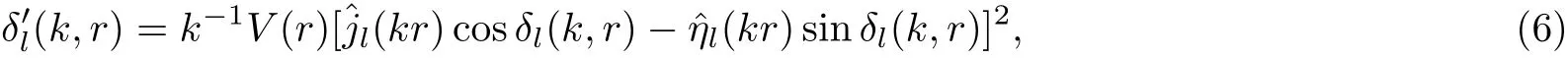
withthe Riccati Bessel functions.Hereindicates the derivative ofwith respect tor.In the phase convention of Calogaro[46]the Riccati Hankel function of first kind is written asThe scattering phase shiftδl(k)is obtained by solving this equation from the origin to the asymptotic region with the initial conditionδl(k,0)=0.The integral equation corresponding to Eq.(6)may be written as

The first order approximation to scattering phase shift reads as

Hereȷl(kr)andηl(kr)stand for the spherical Bessel functions.The scattering phase shifts will be computed by considering Eqs.(6),(8)and(9).
3 Results and Discussions
According to Levinsons theorem[51]each newly introduced bound state raises the zero energy phase shift by 180◦and for reasonable potentials the zero energy phase shifts for higher angular momenta are always integral multiple ofπ.The smaller the resonance width Γ,the stronger is the change in scattering phase shift atE=ER.This implies that at small Γ there is a sharp jump of the phase shift by nearlyπin a very close interval of energies.In the first step of computation all the parametersandwere varied continuously to reproduce a phase shiftfor theα-αsystem andfor theα-3He system in the zero energy limit.For all other states the strength parameterswere given free running,keeping the parametersfixed,to obtain best possible agreement with standard data.[37,49−50]Recently,Li Xuet al.[52]obtained a reasonable description of the elastic scattering of triton by applying systematic helium-3 global optical model potential.Similarly,in this text also the nuclear part of theα-3He andα-3H systems are represented by the same nuclear Hulthén interaction.It is obvious from the fact that the parameters for the nuclear part of the interaction,used in this text,for both the systems are identical.Here we have chosen to work withV0a=0.2758 fm−1forα-αsystem;[49]V0a=0.2364 fm−1forα-3He system;V0a=0.1182 fm−1forα-3H system anda=50 au(atomic unit).Exploiting Eq.(6)along with the parameters in Tabless 1 and 2,we have portrayed the phase shifts for various partial wave states under consideration for theα-α,α-3He,andα-3H systems along with the standard results[37,49−50]in Figs.1–7 respectively.The results for the first and second order Born approximations are also presented in the figures for comparison.
As expected,the S-wave phase shifts for theα-αsystem are positive at low energies and become negative at high energies.The S-wave phase shift changes its sign atELab=19.6 MeV which deviates by 3◦from our earlier work based on exact calculation of the Coulomb plus separable potential[49]but coincides with the results of Refs.[12–13,50]. Beyond 19.6 MeV our phase shifts become negative but possess slightly higher values than those of Ref.[49]up to 70 MeV.In the energy range 70–100 MeV they agree quite well with Ref.[49].The first order Born approximation toδ0changes the sign of the phase shift at about 7 MeV and gradually approaches the values of Ref.[49]as energy increases while the second order approximation produces poor fit to standard data.Our D-wave phase shift reaches its peak value of about 124.915◦atELab=4 MeV in contrast to the standard results[13,49−50]at about 8 MeV.However,beyond 20 MeV our D-wave phase shifts compare well with the earlier work.[49]Our first and second order Born approximations reproduce better fi t with those of Ref.[49]beyond 40 MeV.The G-wave phase shifts are in numerical disagreement with standard data[49−50]in the very low energy range but are in reasonable agreement with those of Ref.[49]beyond 30 MeV.Born approximations to G-wave phase shifts give much lower values than standard results.Although the G-wave phases slightly discern from standard data at low energies,they reproduce correct nature of the phase shift curve.It is observed that our Hulthén potential model is quite capable of producingα-αelastic scattering phases except for the low energy G-wave ones.

Table 1 Parameters for the α-α system.

Table 2 Parameters for the α-3He and α-3H systems.

Fig.1 (Color online)Alpha-alpha phase shifts(δ0,δ2,and δ4)as a function of energy.Experimental data from Refs.[49]and[50].
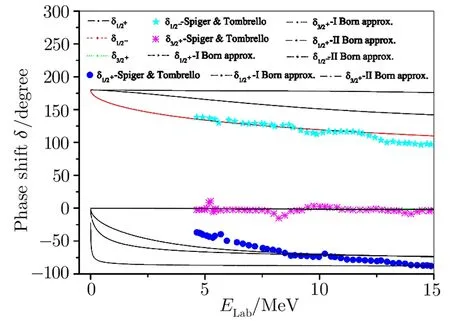
Fig.2 (Color on line)Alpha-3He phase shifts(δ1/2+,δ1/2−,and δ3/2+)as a function of energy.Experimental data from Ref.[37].

Fig.3 (Color on line)Alpha-3He phase shifts(δ3/2− and δ5/2+)as a function of energy. Experimental data from Ref.[37].
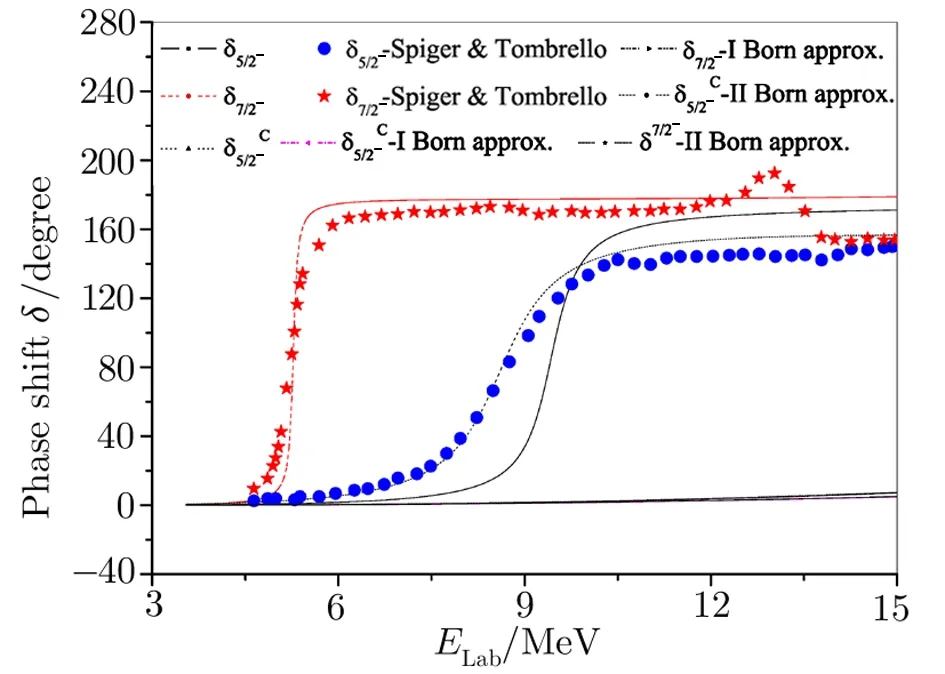
Fig.4 (Color online)Alpha-3He phase shifts(δ5/2− and δ7/2−)as a function of energy. Experimental data from Ref.[37].

Fig.5 (Color on line)Alpha-3H phase shifts(δ1/2+,δ1/2−,and δ3/2+)as a function of energy.Experimental data from Ref.[37].

Fig.6 (Color on line)Alpha-3H phase shifts(δ3/2− and δ5/2+)as a function of energy. Experimental data from Ref.[37].
Forα-3He andα-3H systems the effective potentials vary due to variation in their electromagnetic parts.With these interactions the phase shifts for various angular momentum states have been computed and compared with the standard results.[37,42]It is noticed that the phase shifts computed for different states are in reasonable agreement with the works of Spiger and Tombrello(1967)[37]and Mohr.[42]The phase shiftsδ1/2+forα-3He system differ significantly with those of Ref.[37]in the range 4–7 MeV but agree quite well in the energy range 7 MeV to 12.5 MeV while those for theα-3H system are in good agreement with those of Ref.[37,42].However,the values for thefor both theα-3He andα-3H systems compare well with the standard results[37,42]over the entire energy range.Bothδ3/2+andδ5/2+for the systems under consideration decrease very slowly,almost remain near zero,as energy increases.As forδ5/2−(Figs.4 and 7)significant disagreements with experimental data[37]are observed for both the systems.Out of these two sets of data better results are obtained for theα-3H system as they are comparable with Ref.[37]in the low energy range.However,the nature of ourδ5/2−curve for theα-3He system is very much similar to that of Ref.[42]obtained through a sophisticated model.It reflects that our potential model falls short in producing correct phase shifts for 5/2−states for both theα-3He andα-3H systems.Thus to achieve better agreement in phase shift values with experimental data energy-dependent correction factors are incorporated to the respective interactions.These correction factors areforα-3He andforα-3H systems respectively with the numbers 0.266 and 0.165 in the unit of fm−2.With these correction factors we obtained good agreement with experimental results.[37]The corrected phase shifts are denoted byand are also depicted in Figs.4 and 7.Looking closely into Figs.4 and 7 it is noticed that the values forδ7/2−for theα-3He system compare well with Refs.[37,42]in the low energy range but differ slightly beyond 5.5 MeV,while,on the other hand,the same for theα-3H system discern in the low energy range(up to 6 MeV)but are in good agreement with experimental values[37]beyond 6 MeV.
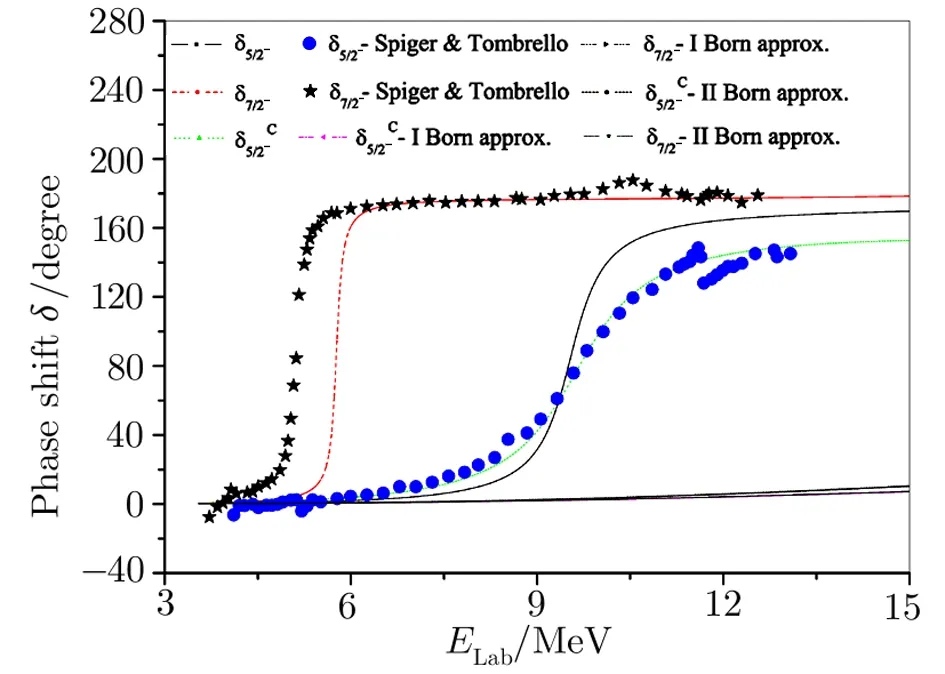
Fig.7 (Color on line)Alpha-3H phase shifts(δ5/2− and δ7/2−)as a function of energy. Experimental data from Ref.[37].
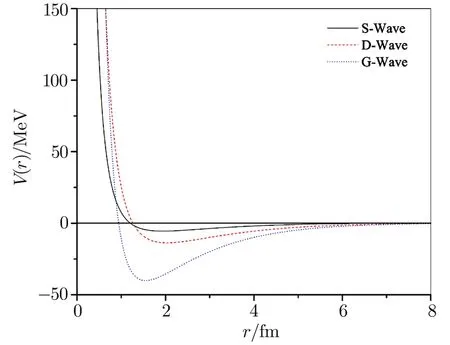
Fig.8 (Color online)Alpha-alpha potentials(for S,P,and D states)as a function of distance.
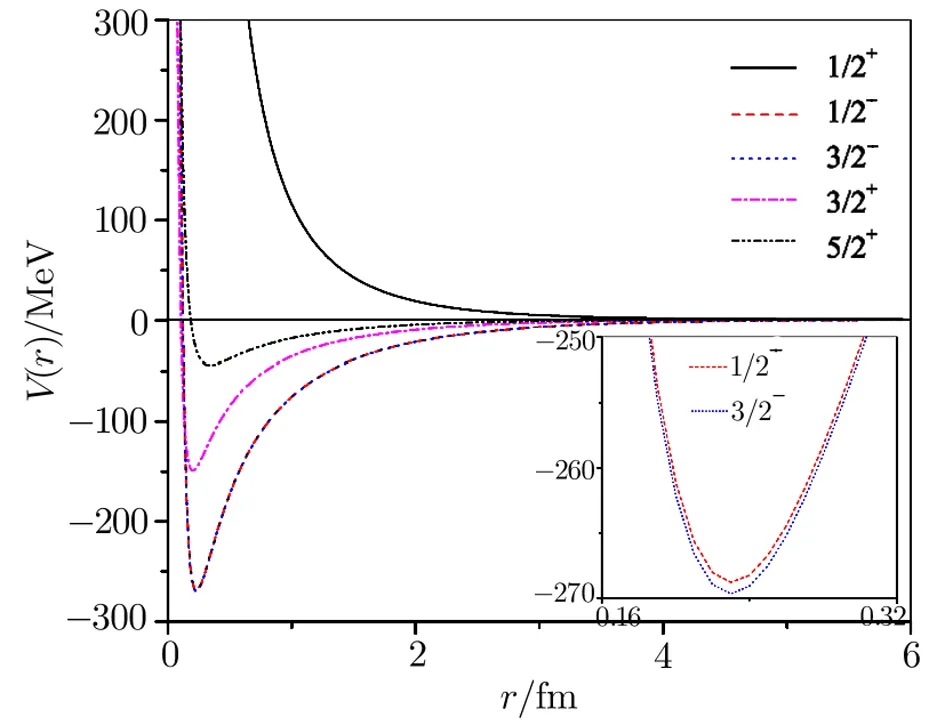
Fig.9 (Color online)Alpha-3He potentials(for 1/2+,1/2−,3/2−,3/2+,and 5/2+states)as a function of distance.
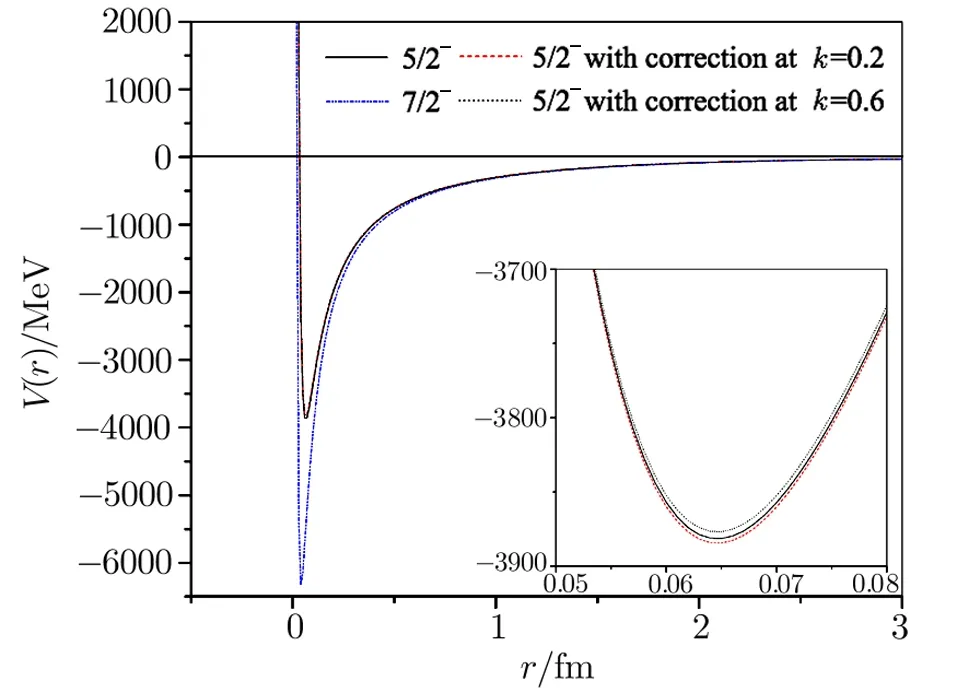
Fig.10 (Color on line)Alpha-3He potentials(for 5/2−and 7/2−states)as a function of distance.
Forα-3He andα-3H systems it is observed that the results for the first order Born approximation is quite comparable to exact calculations except for the 5/2−and 7/2−states,whereas the second order approximations reproduce poor fit to standard data.[49−50]For 3/2+and 5/2+states the differences in phase shift values between exact and approximate calculations are too small to visualize in the scale of the figures as seen in Fig.2.Thus,we have not plotted the results for the Born approximations for the same states in Figs.3,5,and 6.The interactions for the 5/2−and 7/2−states for theα-3He andα-3H systems have sharp depths at small values ofrwhich needs sufficiently high energies for the projectiles to reach that part of the interactions.At low energies only the tail part of the said interactions comes into play and thus produce lower phase shifts.
Plots of the respective effective potentials forα-α,α-3He andα-3H systems are shown in Figs.8–12.The potentials are plotted in MeV units by multiplying Eq.(5)by the factors~2/2m=10.3675 MeV·fm2forα-αand~2/2m=24.190 833 MeV·fm2forα-3He andα-3H systems respectively.From Fig.8 it is seen that our potentials for theα-αsystem possess repulsive cores followed by their attractive parts.The presence of the repulsive cores in the potentials ensures less and less overlap of the particles.As per investigation of Ali and Bodmer[13]the size of the repulsive core as well as the depth of the potential should be decreased with the increase of theℓ-value.In contrast to this,the size of the repulsive cores as well as the depths of our potentials increases with the increment inℓ-value.This may be due the parameterization of the nuclear Hulthén type interaction.The potentials of Bucket al.[26]and of Marquez[28]have very strong attractive parts only.The maximum depth of their potentials is of the order of 125 MeV,while the depth of our S-wave potential is about 5 MeV.Our S-wave phase shifts for theα-αsystem give an indication of resonance at an energy which is far below the barely unbound ground state of8Be.This may be due to the insufficient depth of our S-wave potential.The interactions for the various partial wave states under consideration are depicted in Figs.9–12 for theα-3He andα-3H systems.In Figs.10 and 12 the potentials for 5/2−states with energy-dependent correction factors are also portrayed fork=0.2 fm−1andk=0.6 fm−1respectively.The natures of the potentials for both the systems are same except small differences in their strengths are observed.This is originated due to variation in the electromagnetic parts of the effective interactions forα-3He andα-3H systems.The exceptionally huge depth of our F-wave potentials appear to be consistent with the sharp steps in the 5/2−and 7/2−phase shifts.[37]

4 Conclusion
It is a well-known fact that knowing the general feature of the interactions,various phenomenological potentials with a certain number of free parameters in it can be constructed which are of interest in the cluster model of light nuclei.Variousα-αandα-3He potentials have been proposed earlier with the superposition of repulsive and attractive square well or Gaussian shapes.[26]Kukulinet al.[25]and Marquez[28]were able to fi t theααscattering phase shifts by using Woods-Saxon potential.Apart from square well,Gaussian or Woods-Saxon shapes,we have used here a Hulthén type potential and found reasonable agreement in the phase shift values with the earlier calculations[12−13,37,42,49−50]for theα-α,α-3He andα-3H systems.Also it is noticed that our present model of interaction reproduces better results than our earlier approach.[30]The essential features of the shortrange part of the nucleus-nucleus interaction have been clarified by the microscopic theories like the generator coordinate method(GCM)or the resonating group method(RGM).[53−54]With the RGM,a large number of elastic collisions are described with a good precision[55−56]by using two-body phenomenological interactions.In the RGM there appears an interaction generated from the two-nucleon forces which consists of two parts:(i)a direct part and(ii)a fairly complicated nonlocal kernel.This non-local kernel presents mathematical difficulties for rigorous inclusion of the Coulomb effect in the studies of nucleus-nucleus elastic scattering.Within the framework of RGM,although the numerical complications are considerably higher than the present method,good agreements with the real part of the experimental phase shifts for various partial wave states have been observed.But it seems rather difficult to reproduce the numbers of the RGM calculation by a simple minded potential as used by us.Looking closely into Figs.1,4,and 7 it is observed that our low energy G-wave phase values for theα-αsystem and those for 5/2−states forα-3He andα-3H systems differ slightly from those of Refs.[13,37,49–50],which indicate certain demerits in the potentials for these states.However,good agreements are achieved with the introduction of a correction factor to the potentials of 5/2−states.As it is well known that the fundamental studies of theα-α,α-3He andα-3H interactions provide a useful basis for understanding the interaction between complex nuclei,our potential model may be of considerable interest in treating the complex nucleus-nucleus scattering.In the recent past Nersisyan and Fernndez-Varea[57]applied
[1]E.Rutherford and J.Chadwick,Phil.Mag.4(1927)605.
[2]L.Rosenfeld,Nuclear Forcesa,North-Holland Publ.Co.,Amsterdam(1948).
[3]D.M.Dennison,Phys.Rev.96(1954)378.
[4]F.E.Steigert and M.B.Sampson,Phys.Rev.92(1953)660.
[5]A.E.Glassgold and A.Galonsky,Phys.Rev.103(1956)701.
[6]N.P.Heydenberg and G.M.Temmer,Phys.Rev.104(1956)123.
[7]J.L.Russell,G.C.Phillips,and C.W.Reich,Phys.Rev.104(1956)135.
[8]C.M.Jones,G.C.Phillips,and P.D.Miller,Phys.Rev.117(1960)525.
[9]N.Berk,F.E.Steigert,and G.L.Salinger,Phys.Rev.117(1960)531.
[10]J.R.Dunning,A.M.Smith,and F.E.Steigert,Phys.Rev.121(1961)580.
[11]R.Chiba,H.E.Conzett,H.Morinaga,et al.,Phys.Soc.Japan 16(1961)1077.
[12]T.A.Tombrello and L.S.Senhouse,Phys.Rev.129(1963)2252.
[13]S.Ali and A.R.Bodmer,Nucl.Phys.80(1966)99.
[14]T.A.Tombrello and P.D.Parker,Phys.Rev.131(1963)2582.
[15]T.Kajino and A.Arima,Phys.Rev.Lett.52(1984)739.
[16]P.R.Page,Phys.Rev.C 72(2005)054312.
[17]P.Darriulat,G.Igo,H.G.Pugh,and H.D.Holmgren,Phys.Rev.137(1965)B315.
[18]R.R.Haefner,Rev.Mod.Phys.23(1951)228.
[19]R.Nilson,W.K.Jentschke,G.R.Briggs,et al.,Phys.Rev.109(1958)850.
[20]E.van der Spuy and H.J.Pienaar,Nucl.Phys.7(1958)397.
[21]G.Igo,Phys.Rev.117(1960)1079.
[22]O.Endo,I.Shimodaya,and J.Hiura,Prog.Theor.Phys.(Kyoto)31(1964)1157.second order Born approximation for the computation of scattering phase shifts with electron-ion interaction potential and found some reasonable agreement with exact calculation.But this perturbative approach to the problem is not quite satisfactory in our cases as the strengths of the interactions under consideration are too strong to validate the perturbative approach.Further,also it is of importance to have in the literature the alternative approaches to the problem for calculation of physical observables of a particular system.Thus,it is our belief that the present potential model for the light nuclei systems will be of quite interesting to a wide variety of physicists and deserves some attention.
[23]S.Ali and S.A.Afzal,Nuovo Cimento 50(1967)355.
[24]V.I.Kukulin,V.G.Neudatchin,and Y.F.Smirnov,Nucl.Phys.A 245(1975)429.
[25]B.Buck,H.Friedrich,and C.Wheatley,Nucl.Phys.A 275(1977)246.
[26]H.Friedrich,Phys.Rep.74(1981)209;Phys.Rev.C 30(1984)1102.
[27]L.Marquez,Phys.Rev.C 28(1983)2525.
[28]P.Mohr,et al.,Z.Phys.A-Atomic Nuclei 349(1994)339.
[29]S.Elhatisari,D.Lee,G.Rupak,et al.,Nature(London)528(2015)111.
[30]J.Bhoi and U.Laha,Pramana-J.Phys.88(2017)42.
[31]E.Caurier,P.Navrtil,W.E.Ormand,and J.P.Vary,Phys.Rev.C 64(2001)051301.
[32]T.Yoshida,N.Shimizu,T.Abe,and T.J.Otsuka,Phys.Conf.Ser.454(2013)012050.
[33]T.Myo,A.Umeya,K.Horii,et al.,Prog.Theor.Exp.Phys.(2014)033D01.
[34]V.M.Datar,et al.,Phys.Rev.Lett.111(2013)062502.
[35]P.Mohr,H.Abele,R.Zwiebel,et al.,Phys.Rev.C 48(1993)1420.
[36]A.C.L.Barnard,C.M.Jones,and G.C.Phillip,Nucl.Phys.50(1964)629.
[37]R.J.Spiger and T.A.Tombrello,Phys.Rev.163(1967)964.
[38]L.S.Chuang,Nucl.Phys.A 174(1971)399.
[39]W.R.Boykin,S.D.Baker,and D.M.Hardy,Nucl.Phys.A 195(1972)241.
[40]D.M.Hardy,R.J.Spiger,S.D.Baker,et al.,Nucl.Phys.A 195(1972)250.
[41]R.H.Cyburt and B.Davids,Phys.Rev.C 78(2008)064614.
[42]P.Mohr,Phys.Rev.C 79(2009)065804.
[43]T.Ne ff,Phys.Rev.Lett.106(2011)042502.
[44]U.Laha and J.Bhoi,Phys.Rev.C 91(2015)034614.
[45]S.Flgge,Practical Quantum Mechanics,Springer,Berlin(1971)p.175.
[46]F.Calogero,Variable Phase Approach to Potential Scattering,Academic,New York(1967).
[47]B.Talukdar,D.Chatterjee,and P.Banerjee,J.Phys.G:Nucl.Phys.3(1977)813.
[48]G.C.Sett,U.Laha,and B.Talukdar,J.Phys.A:Math.Gen.21(1988)3643.
[49]U.Laha,N.Haque,T.Nandi,and G.C.Sett,Z.Phys.A-Atomic Nuclei 332(1989)305.
[50]S.A.Afzal,A.A.Z.Ahmad,and S.Ali,Rev.Mod.Phys.41(1969)247.
[51]R.G.Newton,Scattering Theory of Waves and Particles,McGraw Hill,New York(1982).
[52]Y.L.Xu,H.R.Guo,Y.L.Han,and Q.B.Shen,Int.J.Mod.Phys.E 24(2015)1550005.
[53]D.L.Hill and J.A.Wheeler,Phys.Rev.89(1953)1102.
[54]K.Wildermuth and W.McClure,Cluster Representation of Nuclei-Springer Tracts in Modern Physics 41,Springer,New York(1966).
[55]Y.C.Tang,inTopics in Nuclear Physics II,Lecture Notes in Physics,V.145,Springer,Berlin(1981)p.571.
[56]H.Horiuchi,Prog.Theor.Phys.Suppl.62(1977)90.
[57]H.B.Nersisyan and Jos M.Fernndez-Varea,Nucl.Instrum.Methods Phys.Res.B 311(2013)121.
杂志排行
Communications in Theoretical Physics的其它文章
- A New Quantum Gray-Scale Image Encoding Scheme∗
- Phase Transition and Physical Properties of InS∗
- Scalar Hidden-Charm Tetraquark States with QCD Sum Rules∗
- Bilinear Forms and Soliton Solutions for the Reduced Maxwell-Bloch Equations with Variable Coefficients in Nonlinear Optics∗
- Dirac Quasinormal Modes of Static f(R)de Sitter Black Holes∗
- Thermodynamic Geometry of Charged AdS Black Hole Surrounded by Quintessence∗
