A Study of Gaugeon Formalism for QED in Lorentz Violating Background
2018-05-23MushtaqShahandPrinceGanai
Mushtaq B.Shah and Prince A.Ganai
Department of Physics,National Institute of Technology,Srinagar,Kashmir-190006,India
1 Very Special Relativity
By far,there stands no consistent physical model that would provide a pathway to reconcile gravity and quantum mechanics.Methods devised so far to achieve such a theory have not met with any incredible success.The characteristic energy scale corresponding to this scenario is what we call as Planck energy.However,people have always tried to adopt some bypass routes to address few of the theoretical inconsistencies surrounding this scale.One such model is Very Special Relativity(VSR)by Cohen and Glashow.[1]As Lorentz symmetry is found to get broken at Planck scale,VSR dictates that a subgroup of full Lorentz symmetry group could act as a fundamental symmetry of nature.It is believed to preserve the foundations of special relativity.However,we observe a rotational symmetry breaking in VSR scheme.Certain quantum gravity recipes provide substantial clues in this direction.The prominent ones include non-commutative geometry,[2]discrete spacetime,[3]Horava-Lifshitz gravity,[4]spacetime foam models[5]and loop quantum gravity.[6]In the context of string theory,a finite value is obtained for tachyon field expectation value which questions the validity of the theory.Furthermore,an incorrect value emerges for the square of the mass making the approach fl awed.These factors are responsible for Lorentz symmetry breaking.An effective methodology to understand the Lorentz symmetry breaking can be traced to string theory in low energy limit.The corresponding action pertaining to gravity,called super gravity action is known to provide a functional approach.[7]We can exploit this super gravity action to study symmetry breaking using a gravitational Higgs mechanism.It is firmly established that the present structure of fundamental forces can be explicitly handled with gauge theories.Certain approaches have been adopted to study gauge theories in broken spacetime symmetry.We observe a partial symmetry breaking in this format.Also,VSR is expected to explain various issues concerning this broken spacetime symmetry without violating the experimental facts.It is worthwhile to mention that an analysis of non commutative Moyal plane with Poincar symmetry also hints us at some features of Very Special Relativity.A light-like non commutative structure exists in such a construction.[8]
VSR has been found to preserve half of the original supersymmetry when applied to supersymmetry.[9−11]Some interesting results arise when 3-D Yang-Mills and Chern-Simons theory is studied in VSR framework.[12−14]It has also been applied to curved spacetime.[15−16]Study of dark matter with VSR is expected to provide some promising insights.[17]VSR yields a preferred direction in cosmology when applied to FRW equations with anisotropic modification.The results thus obtained are found to be very close to that from the Hubble diagrams.[18]
It has been established that the characteristic feature of VSR symmetric spacetime is that it enables gauge theories to manifest gauge-symmetry.[19−20]Some unphysical degrees of freedom emanate in these gauge theories in VSR-symmetric spacetime as they do in Lorentz spacetime.In order to avoid such invalid physical states,we add a ghost field term in addition to a gauge fixing term in the action of original theories.This modi fi ed action is invariant under BRST transformation.[21−27]As BRST has been shown to have an effective setup to investigate string theories,[28−37]we obtain a BRST symmetric theory using Faddev-Popov method of path integral formulation when adding ghost terms to the original theory.Consequently,we are able to elucidate subspace from total Hilbert space.Although,gravity is said to be symmetric under diffeomorphism transformation,it is quite genuine to expect the physically invalid states to appear while constructing a quantized theory of gravity.BRST transformation is very effective in handling the theory.[38−49]Commonly regarded as third quantized version of loop quantum cosmology,group field cosmology can also be explored with the BRST symmetry.[50−52]As discussed for other gauge theories,supersymmetric gauge theories also su ff er from the problem of super fl uous degrees of freedom;hence some super-ghost fields and super-gauge terms are introduced to get rid of these entities as implied by BRST symmetry transformation.[53−59]Even in the presence of VSR,these physically invalid states still pop up in gauge theories.So,BRST transformation surely finds its use.[60−63]Certain other parameters of this symmetry will be explored for these gauge theories.
In the standard formalism of canonically quantized gauge theories,[64−65]there is a problem of loss of gauge freedom.This is because,we develop a quantum theory only after gauge fi xing,therefore the gauge freedom is sacrificed.Hilbert space structure is different for different gauges.Therefore,we need a wider extension of Hilbert space,which would take different gauges freely for the realization of quantum gauge freedom.A much wider framework for the consideration of quantum gauge freedom was provided by Yokoyama’s gaugeon formalism[66−72]among a family of Lorentz covariant linear gauges.In such formalism,we introduce a bunch of extra fields,namely as gaugeon fields,for purpose of restoring the quantum gauge freedom.Such fields were originally first introduced for QED[66−69]for solving the problem of gauge parameter renormalization.[73]However it was later studied and applied to the Yang-Mills theory[70,72]as well.With the quantum gauge freedom of such formalism at hand,the gauge parameter independence of theS-matrix is clearly manifest.[71]
However,we need to remove the effects of such extra gaugeon modes that renders our Hilbert space unphysical.For this,Gupta-Bleuler type subsidiary condition[64]was originally proposed by Yokoyama.However,such conditions do not work well in presence of interactions.We introduce Faddeev-Popov(FP)ghosts for the gaugeon field as an improved version of the subsidiary conditions of Yokoyama’s formalism for the quantum electrodynamics.Thus,we get a Lagrangian,which is a fully BRST symmetric Lagrangian.We also define a BRST charge,and hence the original subsidiary condition is replaced by the Kugo-Ojima type condition,[66]which works very well even in the interacting case.
Gaugeon formalism and BRST symmetry of the QED Lagrangian density have been discussed.[67]Also,VSR has been explored in various gauge field theories.In this paper,we like to bridge VSR with the BRST discussion of QED.
We organize the paper as follows.In Sec.2,we discuss the gaugeon formalism for QED.In Sec.3,we propose a VSR modi fi ed BRST symmetrized version of this formalism.Also we discuss the relation with Izawa’s theory.We obtain the Lagrangian and Izawa’s Lagrangian using path integral in Sec.4.It is seen here that the reason of introducing the path integral formalism is to assure the existence and necessity of FP ghosts for the gaugeon fields.In the end,we discuss the summary of work.
2 Gaugeon Formalism
We start by writing down the Yokoyama’s Lagrangian density for electromagnetic fieldAµinteracting with charged matter fieldψas
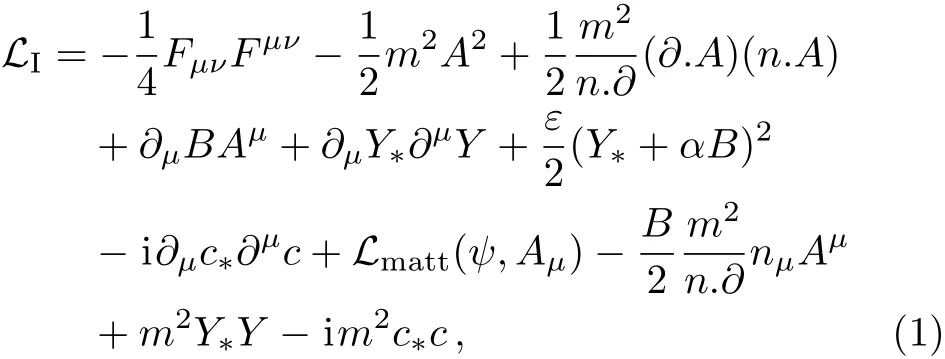
whereFµν=∂µAν −∂νAµis the usual electromagnetic field strength tensor,candc∗are usual FP ghosts,Bis theB- field of Nakanishi-Lautrup,[65]candc∗are usual FP ghosts,YandY∗are scalar gaugeon fields andLmattdescribes the Lagrangian density between theAµand matter fieldψ.We shall start by taking the Abelian limit of Yokoyama’s Lagrangian for the Yang-Mills field.[70,72]In the above expression(1),αrepresents a gauge parameter whereasεrepresents a sign factor(ε=±1).The gauge parameter for such formalism as represented byacan be related withαasa=εα2.For instance,the photon propagator for the above given Yokoyama’s Lagrangian could be written as
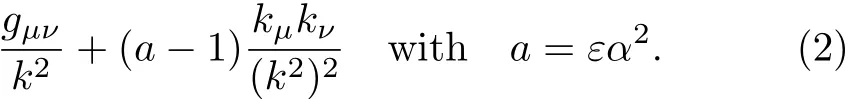
We de fi ne different gauges corresponding to different values ofa.For example,α=0 gives Landau gauge(a=0)andα=1 withε=+1 corresponds to the Feynman gauge(a=1).
Because of the q-number gauge transformation as allowed by the Lagrangian,it gives us freedom to vary gauge parameter.We de fi ne the transformation as
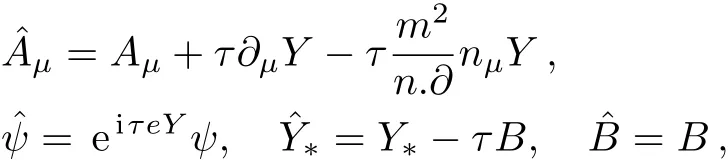

The above equation(4)implies that both the fieldsandsatisfy the same equation of motion.However,for field,the parameterαchanges toαˆ.A change in gauge parameter is obtained using such transformation.In principle,we could choose any value ofα,and fi xα=0 gauge which implies the theory is identical to the Landau-gauge formalism and in addition free ofY-Y∗.
The subsidiary conditions as proposed by Yokoyama[70]restrict to the physical modes as,
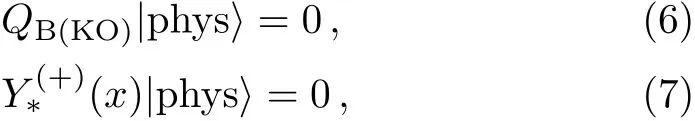
whereQB(KO)represents the BRST charge[66]anddenotes the positive frequency part ofY∗(x).It is important to mention it here that theY∗field satisfies the free field equation

The condition holds good to ensure thatdoes not produce any absurd result and the condition(7)to avoid any contradiction with time evolution.
A more generalized Lagrangian was discussed in the gaugeon formalism[68]by Yokoyama and Kubo that includesB,YandY∗fields.The results showed that there are two types of the theories that allow the q-number gauge transformation.One[Type I]is stated well in(1)and the second[Type II]is described as
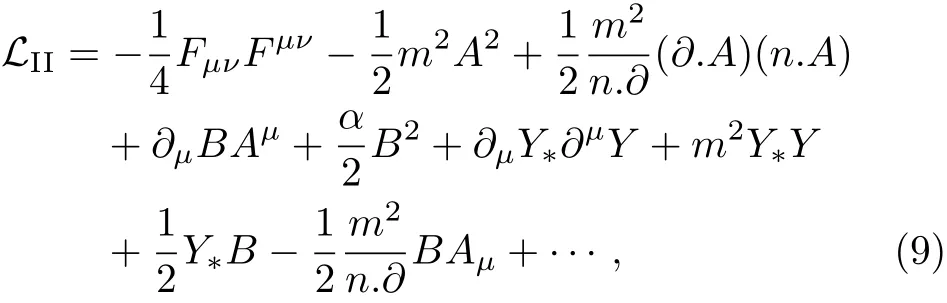
where the matter sector and possible FP ghost term are described by dotted terms.To mention it here that the Lagrangian(9)admits the q-number gauge transformation(3).For the usual canonical formalism:a=α,αinLIIcorresponds to the gauge parameter.q-number gauge transformation gives us freedom of shifting the gauge parameter.Also in Type I theory the sign of the gauge parametera=εα2remains fixed.However,for Type II case,the gaugeon sector avoids any decoupling for arbitrary values of the parameterα.Hence,the equivalence of the standard formalism with this is not that simple as in the Type I theory.
3 Modified BRST Symmetry

Imposing such condition ensures the removal of the additional gaugeon modes as well as the unphysical longitudinal photons from the physical Hilbert space.
We define the q-number gauge transformation as:
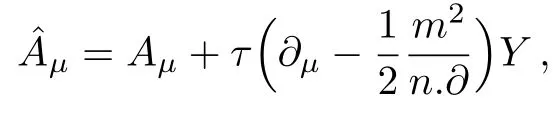
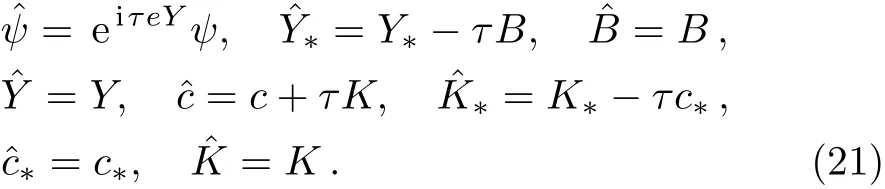
The Lagrangian density does not change its form under such a field transformation,

with a new definition ofαasWith this definition ofalso satisfies the field equations(11)–(16).
It is important to mention here that the BRST transformation(17)commutes with the q-number gauge transformation(21).This results in the fact that BRST charge(19)does not change under the q-number transformation,

Therefore,the physical spaceVphyscorrespondingly does not change with the q-number gauge transformation:

However,this is in complete contrast with the Yokoyama’s partially BRST symmetric theory[70,72]in a way that Yokoyama’s condition(7)changes the form under(3)transformation.
Before we move next,we like to discuss Izawa’s theory.[74]A Lagrangian is given which is BRST symmetric and allows the q-number gauge transformation.We express this BRST symmetric Lagrangian as

Izawa’s Lagrangian can be treated as a prototype for symmetric version of the Type II gaugeon theory,[68]while our Lagrangian is of Type I.Also,arbitrarily choosing any value of gauge parameter,we cannot decouple the gaugeon sector.Thus,it is important to see that the equivalence to the standard formalism in the Landau gauge as seen in Type I theory is not so manifest here.
4 Path Integral Formalism with VSR Modifi cation
We shall start by writing the gauge invariant path integral
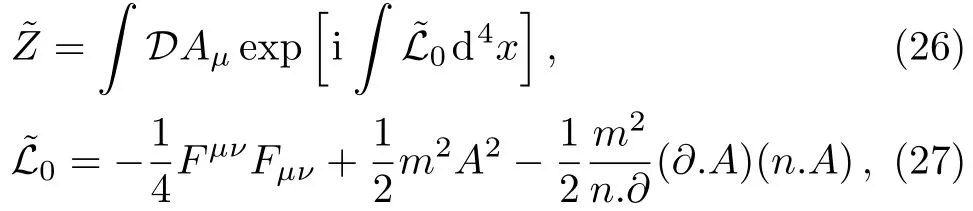
where the matter fieldψis dropped out of the Lagrangian density because it does not contribute substantial to our current discussion.The Faddev-Popov’s trick[75]is written as

and correspondingly the functional determinants are written as


where theδ-functionalδ[F−C]is expressed in the Fourier transformation form(integrated overB).Also,∆FPrepresents the usual Faddeev-Popov determinant.Since the left hand side does not depend on the choice of the functionC,therefore,we can take the’t Hooft averaging[76]overC.Given the weight functional
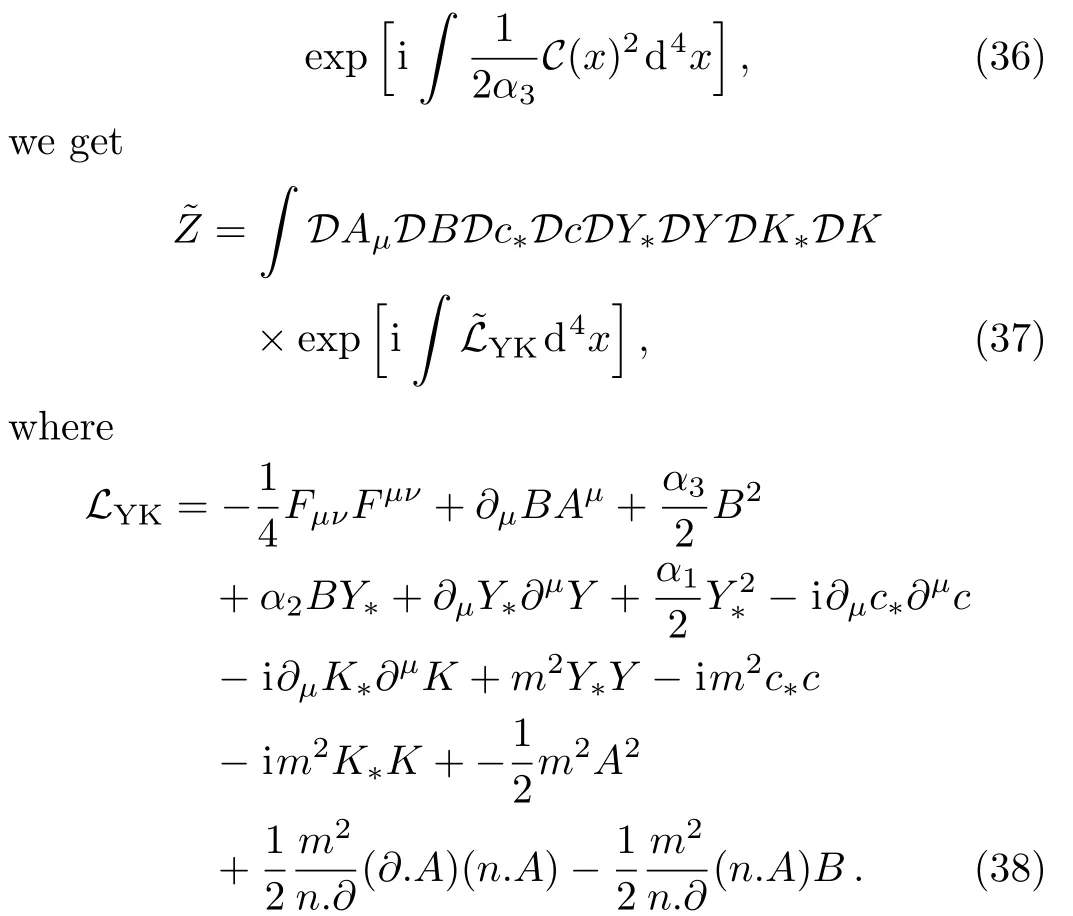
Hence,we get the VSR modified Lagrangian density with three parameters.VSR modified Lagrangian density resembles with the most general Lagrangian density that includes the gaugeon fields namely the three-parameter Lagrangian,[68]up to the FP ghost terms.It is important to mention here that the Lagrangian density(38)remains invariant under the BRST transformation(17).We fi x the values for such parameters,so that we get the Lagrangian density of Type I ifα1=±1=ε,α2=εα,α3=εα2,and ifα1=0,α2=1/2,α3=α,we get Type IIα1=0,α2=1/2,α3=α.(while for other different choice of the parameters,see Ref.[68].)
Thus,using VSR modified path integral approach,we obtain the BRST symmetric Lagrangians of Type I and Type II(Izawa’s Lagrangian).It finds it’s applications mostly in curved space-time.
5 Summary of the Work
We defined a BRST symmetric version for Type I gaugeon formalism for a very simple abelian gauge theory namely quantum electrodynamics in the Lorentz violating background.For this,we introduced gaugeon Faddeev-Popov ghostsKandK∗.We discussed another theory by Izawa,which can be taken as prototype for BRST symmetrized Type II theory.We defined BRST charge and developed a corresponding BRST symmetry,which allows to improve Yokoyama’s subsidiary conditions for generalizing it to the case of interacting fields.In addition,the theory defined above remains invariant under the qnumber gauge transformation unlike Yokoyama’s theory,which is partially BRST symmetric invariant.
We also discussed the path integral formulation of the VSR modified Lagrangian density as well as VSR modified Izawa’s one in Sec.5.Here we show that the gaugeon Faddeev-Popov ghostsKandK∗are essential for the discussion of gaugeon formalism,particularly with the interacting background fields.The whole formalism was done in VSR framework through which makes the Lorentz symmetry breaking is experienced.Regarding future studies,it would be very great to explore AdS/CFT correspondence by investigating the modified AdS spacetime corresponding to its dual CFT in such a Lorentz violating background.[77]It is also possible to study CFT dual to eleven dimensional supergravity on AdS4×S7which would pave way for describing multiple M2 branes.[78−86]Also,a study of BRST symmetry for M-theory and string theory in such a broken spacetime will be very interesting.[87−96]The boundary effects in supersymmetric field theories can be explored as the possibility of some membranes to end on other membranes comes to the fore in the context of string and M-theory.[97−108]Analysing a boundary in the light-like direction in presence of VSR is expected to break half supersymmetry of the theories.As Fadeev-Popov method is unable to handle the nonperturbative effects in Gribov problem,it is possible by constraining path integral to Gribov region using Gribov-Zwanziger approach.[109−112]In the higher dimensional scenario,these non-perturbative infrared properties using Gribov-Zwanziger framework.[113]We can analyze the physics of higher dimensional gauge theories in VSR symmetric spacetime.This means Gribov-Zwanziger method is applicable for such condition.A higher-dimensional VSR can be used to study decoupling solution for gluon propagator using Gribov-Zwanziger approach.
[1]A.G.Cohen and S.L.Glashow,Phys.Rev.Lett.97(2006)021601.
[2]G.Amelino-Camelia,J.R.Ellis,N.E.Mavromatos,et al.,Nature(London)393(1998)763,[astro-ph/9712103].
[3]R.Gambini and J.Pullin,Phys.Rev.D 59(1999)124021,[gr-qc/9809038].
[4]S.M.Carroll,J.A.Harvey,V.A.Kostelecky,et al.,Phys.Rev.Lett.87(2001)141601,[hep-th/0105082].
[5]P. Horava, Phys. Rev. D 79 (2009) 084008,[arXiv:0901.3775[hep-th]].
[6]V.A.Kostelecky and S.Samuel,Phys.Rev.D 39(1989)683.
[7]S.Chakravarty,K.Dasgupta,O.J.Ganor,and G.Rajesh,Nucl.Phys.B 587(2000)228,[hep-th/0002175].
[8]V.A.Kostelecky and S.Samuel,Phys.Rev.D 40(1989)1886.
[9]A.G.Cohen and S.L.Glashow,Phys.Rev.Lett.97(2006)021601,[hep-ph/0601236].
[10]M.M.Sheikh-Jabbari and A.Tureanu,Phys.Rev.Lett.101(2008)261601,[arXiv:0806.3699[hep-th]].
[11]A.G.Cohen and D.Z.Freedman,J.High Energy Phys.0707(2007)039,[hep-th/0605172].
[12]S.Petras,R.von Unge,and J.Vohanka,J.High Energy Phys.1107(2011)015,[arXiv:1102.3856[hep-th]].
[13]J.Vohanka,Phys.Rev.D 85(2012)105009.
[14]J.Vohnka and M.Faizal,Eur.Phys.J.C 75(2015)592,[arXiv:1503.04761[hep-th]].
[15]J.Vohnka and M.Faizal,Nucl.Phys.B 904(2016)327,[arXiv:1505.08112[hep-th]].
[16]J.Vohnka and M.Faizal,Phys.Rev.D 91(2015)045015,[arXiv:1409.6334[hep-th]].
[17]A.P.Kouretsis,M.Stathakopoulos,and P.C.Stavrinos,Phys.Rev.D 79(2009)104011,[arXiv:0810.3267[gr-qc]].
[18]W.Muck,Phys.Lett.B 670(2008)95,[arXiv:0806.0737[hep-th]].
[19]D.V.Ahluwalia and S.P.Horvath,J.High Energy Phys.1011(2010)078.
[20]Z.Chang,M.H.Li,X.Li,and S.Wang,Eur.Phys.J.C 73(2013)2459,[arXiv:1303.1593[astro-ph.CO]].
[21]J.Alfaro and V.O.Rivelles,Phys.Rev.D 88(2013)085023,[arXiv:1305.1577[hep-th]].
[22]J.Alfaro,P.Gonzlez,and R.Vila,Phys.Rev.D 91(2015)105007,Addendum:[Phys.Rev.D 91(2015)129904],[arXiv:1504.04222[hep-ph]].
[23]C.Becchi,A.Rouet,and R.Stora,Annals Phys.98(1976)287.
[24]I.V.Tyutin,arXiv:0812.0580[hep-th].
[25]G.Costa,J.Julve,T.Marinucci,and M.Tonin,Nuovo Cim.A 38(1977)373.
[26]T.Kugo and I.Ojima,Phys.Lett.73B(1978)459.
[27]H.Hata and T.Kugo,Nucl.Phys.B 158(1979)357.
[28]M.Faizal and M.Khan,Eur.Phys.J.C 71(2011)1603,[arXiv:1103.0221[hep-th]].
[29]L.Baulieu and J.Thierry-Mieg,Nucl.Phys.B 197(1982)477.
[30]T.Azevedo and R.L.Jusinskas,J.High Energy Phys.1608(2016)133,[arXiv:1607.06805[hep-th]].
[31]C.R.Mafra and O.Schlotterer,J.High Energy Phys.1604(2016)148,[arXiv:1603.04790[hep-th]].
[32]R.L.Jusinskas,J.High Energy Phys.1512(2015)136,[arXiv:1510.05268[hep-th]].
[33]R.L.Jusinskas,J.High Energy Phys.1605(2016)116[arXiv:1604.02915[hep-th]].
[34]I.Oda,Mod.Phys.Lett.A 18(2003)1023.
[35]M.Faizal,J.High Energy Phys.1301(2013)156,[arXiv:1301.4305[hep-th]];M.Faizal,Mod.Phys.Lett.A 27(2012)1250147,[arXiv:1207.2120[hep-th]].
[36]M.Faizal,Commun.Theor.Phys.57(2012)637,[arXiv:1201.1220[hep-th]].
[37]M. Faizal, Phys. Rev. D 84 (2011) 106011,[arXiv:1111.0213[hep-th]].
[38]M.Faizal,Int.J.Mod.Phys.A 28(2013)1350012,[arXiv:1301.5664[math-ph]].
[39]M.Faizal and D.J.Smith,Phys.Rev.D 85(2012)105007,[arXiv:1112.6070[hep-th]].
[40]M.Faizal,S.Upadhyay,and B.P.Mandal,“IR ys.J.C 76(2016)189,[arXiv:1604.00390[hep-th]].
[41]L.N.Chang and C.P.Soo,Phys.Rev.D 46(1992)4257,[hep-th/9203014].
[42]S.Kachru,Nucl.Phys.B 390 (1993)173,[hepth/9204053].
[43]H.Terao,Nucl.Phys.B 395 (1993)623,[hepth/9205030].
[44]H.Y.Lee,A.Nakamichi,and T.Ueno,Phys.Rev.D 47(1993)1563,[hep-th/9205066].
[45]N.Ohta and H.Suzuki,Mod.Phys.Lett.A 7(1992)2723,[hep-th/9205101].
[46]D.Anselmi and P.Fre,Nucl.Phys.B 392(1993)401,[hep-th/9208029].
[47]M.Faizal,Mod.Phys.Lett.A 27(2012)1250075,[arXiv:1204.0295[gr-qc]].
[48]M.Faizal,Phys.Lett.B 705(2011)120,[arXiv:1109.3443[gr-qc]].
[49]M.Faizal,J.Phys.A 44(2011)402001,[arXiv:1108.2853[gr-qc]].
[50]M.Faizal,Found.Phys.41(2011)270,[arXiv:1010.1143[gr-qc]].
[51]M.Faizal,Mod.Phys.Lett.A 28(2013)1350034,[arXiv:1302.5156[gr-qc]].
[52]M.Faizal,Grav.Cosmol.20(2014)132,[arXiv:1303.5478[gr-qc]].
[53]M.Faizal,Int.J.Geom.Meth.Mod.Phys.11(2014)1450010,[arXiv:1301.0224[gr-qc]].
[54]M.Faizal,Class.Quant.Grav.29 (2012)215009,[arXiv:1209.2346[gr-qc]].
[55]J.Troost,J.High Energy Phys.1107(2011)042,[arXiv:1102.0153[hep-th]].
[56]M.Faizal,Commun.Theor.Phys.58(2012)704,[arXiv:1207.6564[hep-th]].
[57]R.Banerjee and S.Deguchi,J.Math.Phys.51(2010)052301,[arXiv:0905.3050[hep-th]].
[58]K.Ulker,Phys.Rev.D 68 (2003)085005,[hepth/0304154].
[59]M.B.Shah,M.Faizal,P.A.Ganai,et al.,Eur.Phys.J.C 77(2017)309.
[60]A.C.Lehum,J.R.Nascimento,A.Y.Petrov,and A.J.daSilva,Phys.Rev.D 88 (2013)045022,[arXiv:1305.1812[hep-th]].
[61]P.Weinreb and M.Faizal,Phys.Lett.B 748(2015)102,[arXiv:1506.07618[hep-th]].
[62]S.Upadhyay and P.K.Panigrahi,Nucl.Phys.B 915(2017)168,[arXiv:1608.03947[hep-th]].
[63]S.Upadhyay,M.B.Shah,and P.A.Ganai,Eur.Phys.J.C 77(2017)157,[arXiv:1702.05755[hep-th]].
[64]N.Nakanishi,Phys.Rev.D 5(1972)1324.
[65]T.Kugo and I.Ojima,Phys.Lett.73B(1978)459;Prog.Theor.Phys.60(1978)1896;Prog.Theor.Phys.Suppl.66(1979).
[66]K.Yokoyama,Prog.Theor.Phys.51(1974)1956.
[67]M.Koseki,M.Sato,and R.Endo,Prog.Theor.Phys.90(1993)1111.
[68]K.I.Yokoyama and R.Kubo,Prog.Theor.Phys.52(1974)290.
[69]K.Yokoyama,Quantum Electrodynamics,(in Japanese),Iwanami Shoten,Tokyo(1978).
[70]K.I.Yokoyama,Prog.Theor.Phys.59(1978)1699;K.Yokoyama,M.Takeda,and M.Monda,Prog.Theor.Phys.60(1978)927;K.Yokoyama,Prog.Theor.Phys.60(1978)1167.
[71]K.I.Yokoyama,Phys.Lett.79B(1978)79.
[72]K.I.Yokoyama,M.Takeda,and M.Monda,Prog.Theor.Phys.64(1980)1412.
[73]M.Hayakawa and K.Yokoyama,Prog.Theor.Phys.44(1970)533.
[74]K.I.Izawa,Prog.Theor.Phys.88(1992)759.
[75]L.D.Faddeev and V.N.Popov,Phys.Lett.25B(1967)29.
[76]G.’t Hooft,Nucl.Phys.B 33(1971)173.
[77]J.M.Maldacena,Int.J.Theor.Phys.38(1999)1113,[Adv.Theor.Math.Phys.2(1998)231],[hepth/9711200].
[78]A.Gustavsson,J.High Energy Phys.0804(2008)083,[arXiv:0802.3456[hep-th]].
[79]J.Bagger and N.Lambert,J.High Energy Phys.0802(2008)105,[arXiv:0712.3738[hep-th]].
[80]J.Bagger and N.Lambert,Phys.Rev.D 77(2008)065008,[arXiv:0711.0955[hep-th]].
[81]M. Faizal, Europhys. Lett. 98 (2012) 31003,[arXiv:1204.1191[hep-th]].
[82]O.Aharony,O.Bergman,D.L.Ja ff eris,and J.Maldacena,J.High Energy Phys.0810(2008)091,[arXiv:0806.1218[hep-th]].
[83]O.Aharony,O.Bergman,and D.L.Ja ff eris,J.High Energy Phys.0811(2008)043,[arXiv:0807.4924[hep-th]].
[84]M. Faizal, Nucl. Phys. B 869 (2013) 598,[arXiv:1301.0223[hep-th]].
[85]J.M.Queiruga,A.C.Lehum,and M.Faizal,Nucl.Phys.B 902(2016)58,[arXiv:1511.03586[hep-th]].
[86]E.Antonyan and A.A.Tseytlin,Phys.Rev.D 79(2009)046002,[arXiv:0811.1540[hep-th]].
[87]T.Azevedo and R.L.Jusinskas,J.High Energy Phys.1608(2016)133,[arXiv:1607.06805[hep-th]].
[88]C.R.Mafra and O.Schlotterer,J.High Energy Phys.1604(2016)148,[arXiv:1603.04790[hep-th]]
[89]R.L.Jusinskas,J.High Energy Phys.1512(2015)136,[arXiv:1510.05268[hep-th]].
[90]R.L.Jusinskas,J.High Energy Phys.1605(2016)116,[arXiv:1604.02915[hep-th]].
[91]I.Oda,Mod.Phys.Lett.A 18(2003)1023.
[92]M.Faizal,J.High Energy Phys.1301(2013)156,[arXiv:1301.4305[hep-th]].
[93]M.Faizal,Mod.Phys.Lett.A 27(2012)1250147,[arXiv:1207.2120[hep-th]].
[94]M.Faizal,Commun.Theor.Phys.57(2012)637,[arXiv:1201.1220[hep-th]].
[95]M. Faizal, Phys. Rev. D 84 (2011) 106011,[arXiv:1111.0213[hep-th]].
[96]M.Faizal,Int.J.Mod.Phys.A 28(2013)1350012.
[97]D.S.Berman,M.J.Perry,E.Sezgin,and D.C.Thompson,J.High Energy Phys.1004(2010)025,[arXiv:0912.3504[hep-th]].
[98]F.Aprile and V.Niarchos,J.High Energy Phys.1607(2016)126,[arXiv:1604.01561[hep-th]].
[99]M.Faizal,J.High Energy Phys.1204(2012)017,[arXiv:1204.0297[hep-th]].
[100]D.V.Belyaev and P.van Nieuwenhuizen,J.High Energy Phys.0809(2008)069,[arXiv:0806.4723[hep-th]].
[101]M.Faizal,Y.Luo,D.J.Smith,et al.,Nucl.Phys.B 914(2017)577,[arXiv:1601.05429[hep-th]].
[102]M.Faizal,Mod.Phys.Lett.A 29(2014)1450154,[arXiv:1303.5477[hep-th]].
[103]D.S.Berman and D.C.Thompson,Nucl.Phys.B 820(2009)503,[arXiv:0904.0241[hep-th]].
[104]M.Faizal and D.J.Smith,Phys.Rev.D 87(2013)025019,[arXiv:1211.3654[hep-th]].
[105]A.Bilal,J.High Energy Phys.1111(2011)046,[arXiv:1103.2280[hep-th]].
[106]D.V.Belyaev and T.G.Pugh,J.High Energy Phys.1010(2010)031,[arXiv:1008.1574[hep-th]].
[107]M.Faizal and A.Awad,Phys.Lett.B 748(2015)414,[arXiv:1502.07717[hep-th]].
[108]D.V.Belyaev and P.van Nieuwenhuizen,J.High Energy Phys.0804(2008)008,[arXiv:0801.2377[hep-th]].
[109]D.Zwanziger,Nucl.Phys.B 209(1982)336.
[110]D.Zwanziger,Nucl.Phys.B 323(1989)513.
[111]M.A.L.Capri,D.Dudal,A.D.Pereira,et al.,Phys.Rev.D 95(2017)045011.
[112]D.Zwanziger,Nucl.Phys.B 321(1989)591.
[113]M.S.Guimaraes,A.D.Pereira,and S.P.Sorella,Phys.Rev.D 94(2016)116011,[arXiv:1608.06979[hep-th]].
杂志排行
Communications in Theoretical Physics的其它文章
- A New Quantum Gray-Scale Image Encoding Scheme∗
- Phase Transition and Physical Properties of InS∗
- Parameterization of Nuclear Hulthén Potential for Nucleus-Nucleus Elastic Scattering
- Scalar Hidden-Charm Tetraquark States with QCD Sum Rules∗
- Bilinear Forms and Soliton Solutions for the Reduced Maxwell-Bloch Equations with Variable Coefficients in Nonlinear Optics∗
- Dirac Quasinormal Modes of Static f(R)de Sitter Black Holes∗
