Bilinear Forms and Soliton Solutions for the Reduced Maxwell-Bloch Equations with Variable Coefficients in Nonlinear Optics∗

Jun Chai(柴俊),Bo Tian(田播), and Han-Peng Chai(柴汉鹏)

State Key Laboratory of Information Photonics and Optical Communications,and School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China

1 Introduction

Nonlinear evolution equations have attracted a lot of attentions since they are able to describe the nonlinear phenomena in many fields of sciences and engineering.[1−3]

Recently,people have shown their interests in nonlinear optics.[4−5]In the communication-grade optical fiber or optical-transmitting medium,there exists the attenuation,so that the optical loss is inevitable and the pulse is deteriorated by this loss.[6]As we know,the selfinduced transparency(SIT)phenomenon plays a role in overcoming the attenuation in the optical communication systems.[7]Researchers have pointed out that the reduced Maxwell-Bloch(RMB)equations can be applied to get for the phenomenon of SIT,a more accurate description compared to the so-called SIT equations.[8−12]

In this paper,we will study the RMB equations with variable coefficients,[10]written as

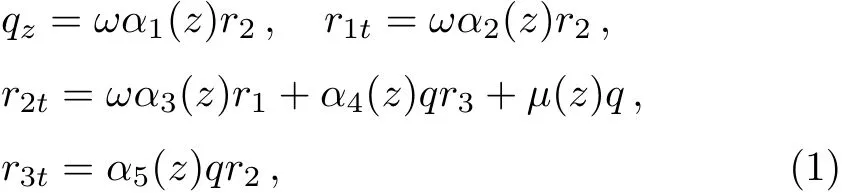
describing the propagation of the intense ultra-short optical pulses through an inhomogeneous two-level dielectric medium,whereqis the inhomogeneous electric field,r1andr2denote the real and imaginary parts of the polarization of the two-level medium,respectively,r3represents the(real)population difference between the ground and excited states,the subscriptszandtrespectively refer to the partial derivatives with respect to the scaled distance and time,ωdenotes the resonance frequency,αj(z)’s(j=1,2,...,5)are the functions related to the inhomogeneous electric field,andµ(z)is the function related to the two-level medium.Painlevé integrable condition,Lax pair,in finitely-many conservation laws and Darboux transformation for Eqs.(1)have been derived.[10]

The outline of this paper is as follows.In Sec.2,via the Hirota method,[13−15]and symbolic computation,[16−17]introducing the dependent variable transformations,we will derive the variable-coefficient-dependentbilinear forms for Eqs.(1).In Sec.3,based on those bilinear forms,the soliton solutions in analytic forms will be constructed.Section 4 will be our conclusions.

2 Bilinear Forms

Introducing the dependent variable transformations

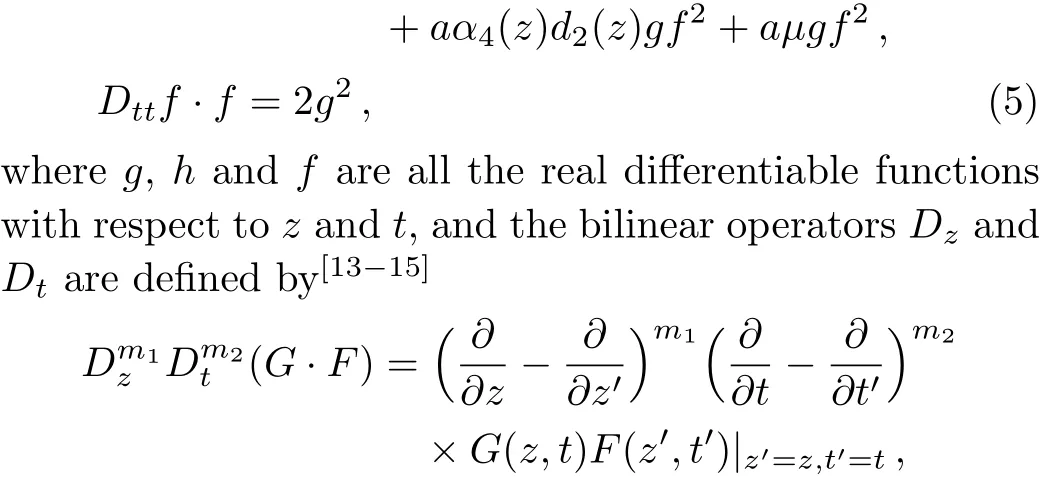
withG(z,t)as the differentiable function ofzandt,as the differentiable function of the formal variablesas the non-negative integers.

3 Soliton Solutions

In the following,based on bilinear forms(5),we will construct the soliton solutions for Eqs.(1),by expandingg,fandhwith respect to a formal expansion parameterεas

where2,4,6,...)are the real differentiable functions with respect tozandt.

3.1 One-Soliton Solutions

To derive the one-soliton solutions for Eqs.(1),we truncate expressions(6)as,substitute them into bilinear forms(5),and derive the one-soliton solutions for Eqs.(1)as

3.2 Two-Soliton Solutions

For the two-soliton solutions,we truncate expressions(6)asandsubstitute them into bilinear forms(5),and obtain

withρk(z)’s as the real functions andσk’s as the real constants.

3.3 N-Soliton Solutions

The vectorN-soliton solutions for Eqs.(1)can be expressed as

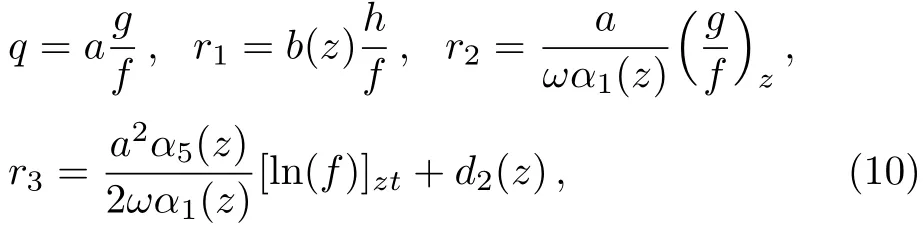
under constraints(3)and(8),where

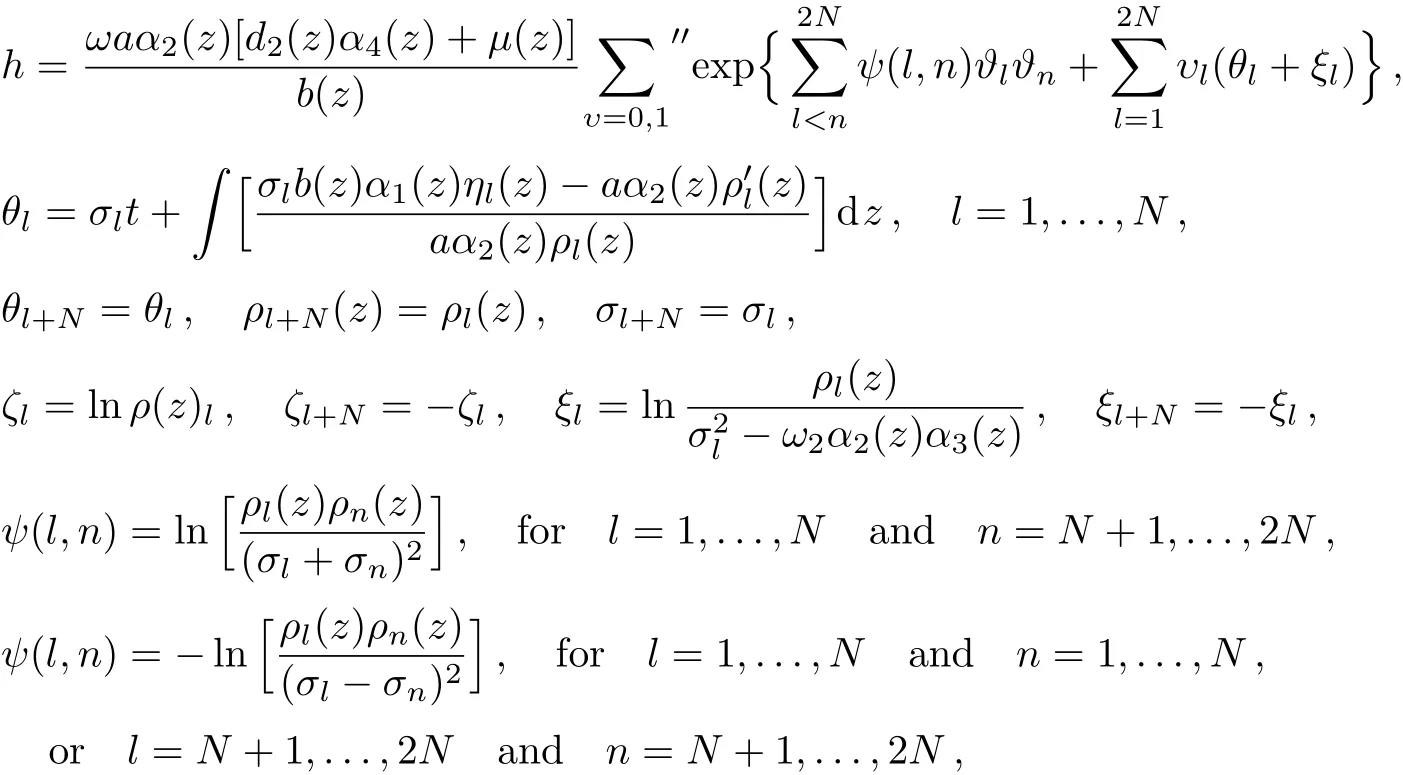
withρl(z)’s being the real functions andσl’s being the real constants,denoting the summation over all the possible pairs taken from the 2Nelements with the conditionindicating the summations over all the possible combinations ofυl=0,1 and satisfying

4 Conclusions

In this paper,we have studied the RMB equations with variable coefficients,i.e.,Eqs.(1),describing the propagation of the intense ultra-short optical pulses through an inhomogeneous two-level dielectric medium.Through the Hirota method and symbolic computation in this paper,via transformations(2),we have derived variable-coefficient-dependent bilinear forms(5)under constraints(3).Then,based on bilinear forms(5),under constraints(3)and(8),the analytic one-,two-andN-soliton solutions,i.e.,solutions(7)–(10),have been constructed.

Acknowledgments

We express our sincere thanks to the Editors and Reviewers for their valuable comments.

[1]M.J.Ablowitz and P.A.Clarkson,Solitons,Nonlinear Evolution Equations and Inverse Scattering,Cambridge University Press,Cambridge(2004).

[2]H.Q.Hao,R.Guo,and J.W.Zhang,Nonlinear Dyn.88(2017)1615.

[3]H.H.Zhao,X.J.Zhao,and H.Q.Hao,Appl.Math.Lett.61(2016)8.

[4]Z.J.Yang,Z.F.Yang,J.X.Li,et al.,Res.Phys.7(2017)1485.

[5]R.Guo and H.Q.Hao,Commun.Nonlinear Sci.Numer.Simul.18(2013)2426.

[6]K.Porsezian,P.Seemuvasakumaran,and R.Ganapathy,Phys.Lett.A 348(2006)233.

[7]V.V.Kozlov and J.H.Eberly,Opt.Commun.179(2000)85..

[8]L.Mandel and E.Wolf,Coherence in Quantum Optics,Plenum Press,New York(1978).

[9]H.Steudel,A.A.Zabolotskii,and R.Meinel,Phys.Rev.E 72(2005)056608.

[10]H.Q.Hao and J.W.Zhang,Commun.Nonlinear Sci.Numer.Simul.22(2015)1350.

[11]A.Bekir,Chaos,Solitons&Fractals 32(2007)449.

[12]H.Steudel,A.A.Zabolotskii,and R.Meinel,Phys.Rev.E 72(2005)056608.

[13]R.Hirota,J.Math.Phys.14(1973)805.

[14]R.Hirota and Y.Ohta,J.Phys.Soc.Jpn.60(1991)798.

[15]R.Hirota,The Direct Method in Soliton Theory,Cambridge University Press,Cambridge(2004).

[16]W.P.Hong,Phys.Lett.A 361(2007)520.

[17]G.C.Das and J.Sarma,Phys.Plasmas 6(1999)4394.