Investigation of Bose-Einstein Condensates in q-Deformed Potentials with First Order Perturbation Theory

Ferhat Nutku and Ekrem Aydıner

Department of Physics,Faculty of Science˙Istanbul University,Vezneciler,˙Istanbul,34134,Turkey

1 Introduction

Bose-Einstein condensation(BEC)of ultracold conifned interacting dilute bosonic gases have attracted a lot of attention both theoretically and experimentally.[1−3]BEC in a 3D box is a second order phase transition,which occurs at a critical temperatureTc,which is proportional to particle density with(N/V)2/3term.The condensation temperature of ideal and interacting bosonic gases can be computed by analytically or numerically.Bosonic particles can spontaneously form a BEC atTcin three dimension,however BEC does not occur at two and one-dimensional space without external potentials.In order to obtain BEC at any dimension,magnetic harmonic and/or harmonic potentials can be used. Furthermore,various trapping potentials lead to different shape of condensates such as one-dimensional,[4−5]twodimensional,[2]disk-shaped[6−7]or cigar-shaped.[7]According to the type of trapping potential,stabilization of many particle states occurs as a solution type of solitons,[4,8−10]vortices[11]and vortexes.[12]On the other hand,BECs are studied for in a various aspects,such as phase coherence,[13]phase coherent ampli fi cation of matter waves,[14−16]fl uctuations,[17]matter-wave di ff raction.[18]BEC for interacting particles have also been studied for different potentials such as Morse,Pöschl-Teller and elliptic function potentials,[19−20]except from harmonic and optical potentials.Finding a solution for these potentials is more difficult than harmonic or optical lattice potentials.Therefore,in general,numerical solutions are employed to Gross-Pitaevskii equation to find approximate solutions for wave functions and ground state energies at critical temperature.[21−23]The formation of BECs under several type of potentials,theirTcvalues,ground state populations and heat capacity values are investigated in Ref.[19].Furthermore,in Ref.[19],Tcand condensate fraction expressions have been calculated for weakly interacting Bose gas in an effective external potential.

Recently,q-deformed potentials are highly attracting and investigated by several authors afterq-deformed hyperbolic ones have been proposed by Arai.[24−25]This kind of potentials can be created by destroying symmetry of the potential with wave mixing.The main route ofq-deformed quantum mechanics[26−27]was developed by generalizing the standard quantum mechanics,which was based on the Heisenberg formalism.By usingq-deformation,several quantum mechanical phenomena such as uncertainty relation,[28−29]coherent states,[28,30−31]density matrix usingq-boson oscillator coherent states,[32]hydrogen atom[33]were investigated.After the introduction ofq-deformed harmonic oscillator,[30]q-deformed potentials have found applications in physics and chemistry such as explaining weak localization and magnetoresistance in semiconductors,[34]vibrational spectra of diatomic[35]and polyatomic molecules.[36]

q-deformed potentials have also been used to model BEC.For example,q-deformed potentials present promising applications for modeling the atom-trapping potentials in BECs.[37]Theq-deformation of the Morse potential is investigated in Ref.[38],the solutions of Schrödinger equation under variousq-deformed potentials are investigated in Refs.[39–41].However,as our knowledge,q-deformed potentials have never been studied to analyze the solution of one-dimensional Gross-Pitaevskii equation based on first order perturbation expansion method.In this study,we obtainedq-parameter dependent dark soliton solutions under these type of potentials.

The structure of article is as the following;beforehand a brief outline of perturbation solution method is given in Sec.2.Afterwards in Sec.3,the definition ofq-deformed potential is presented with various examples.Dark and bright soliton wave-function solutions obtained by the application of first order perturbation method are also included in Sec.3.The change of the probability distribution of single particle is given in Results and Discussion section for various potentials.

2 First Order Perturbation Solution

Single particle behaviour in a BEC is explained by Groos-Pitaevskii equation.[23]In one dimension,Gross-Pitaevskii equation or in the literature usually called the nonlinear Schrödinger equation is given as the following,

whereThis is the special case of the Jacobi elliptic function sn(x,k)withk=1.x0is the integration constant and it is set to zero.This type of solution is called as dark soliton and theψ0is the zero ordered perturbation term.In order to find the first order perturbative solution,is put into Eq.(4)divided by 2ϵand the limitis taken then this will give

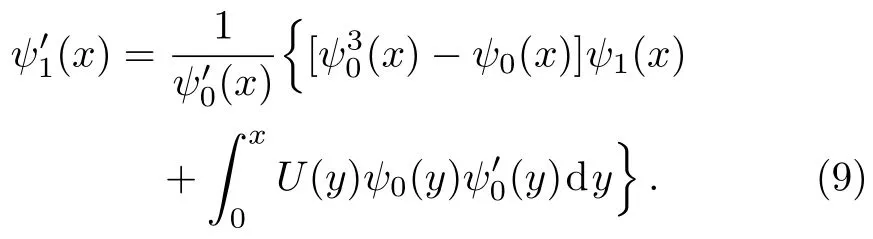
The solution of the above first order linear differential equation can be obtained by using integrating factor method.The solution of the following equation

Finallyψ(x)=ψ0(x)+ϵψ1(x)will give the first order perturbation solution.

3q-Deformed Potentials

Theq-deformed hyperbolic functions are first mentioned by Arai[24−25]and they are composed ofq-deformed exponential functions defined by the following equations,Arai defined these functions in his study on exactly solvable supersymmetric quantum mechanics.

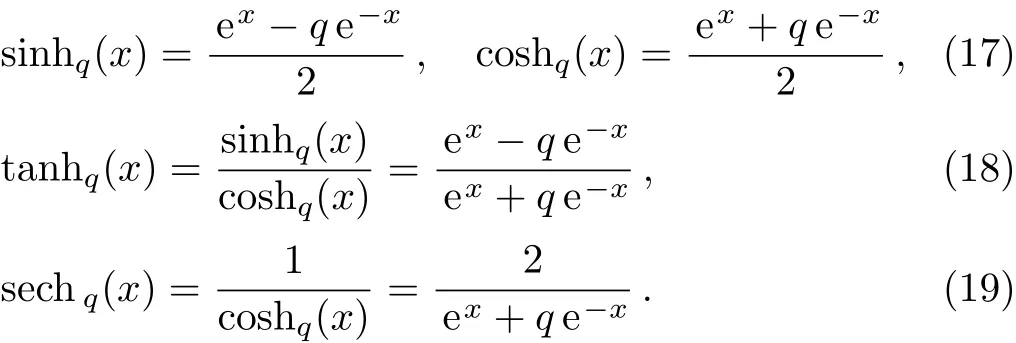
q-deformed Manning-Rosen potential is composed ofq-deformed hyperbolic functions.In our work we used the following modi fi ed version ofq-deformed Manning-Rosen potential,which provides a solution in the used perturbation method,

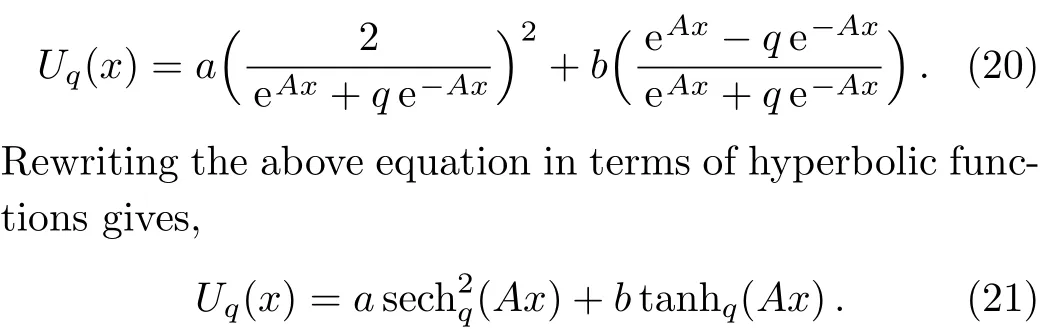
From Eq.(21)one can derive several type of potentials.Ifa<0,b>0,andq=1,Eq.(21)gives Rosen-Morse,

The pro fi le ofq-deformed Rosen-Morse and Pöschl-Teller potentials are given in Figs.1(a)and 1(b)respectively.

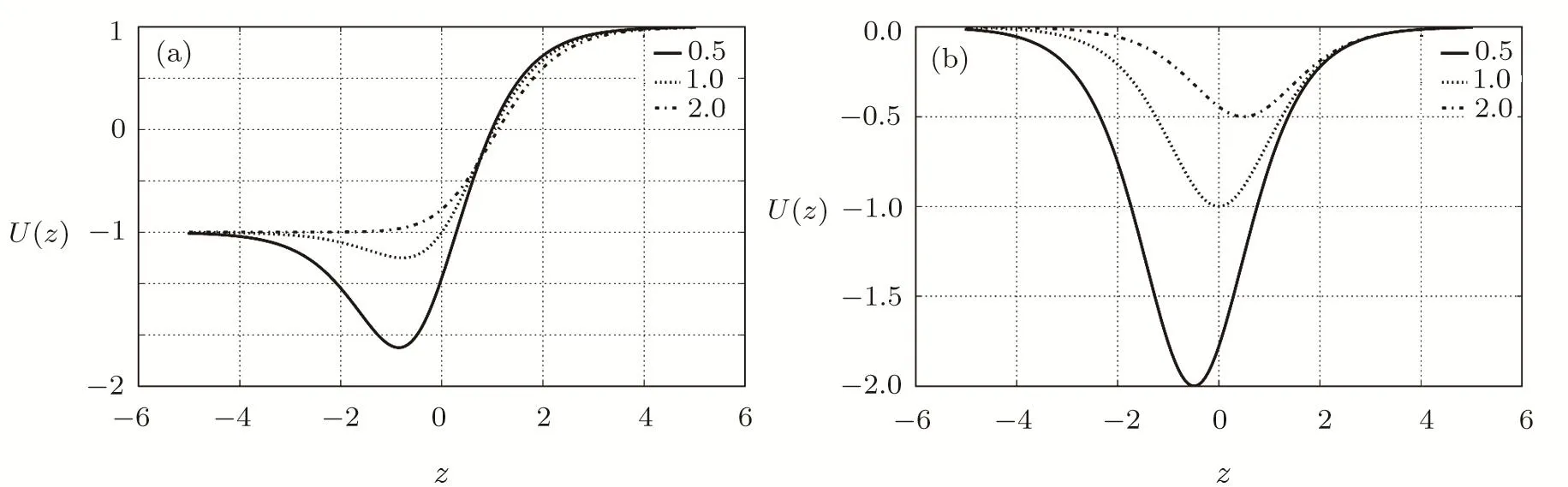
Fig.1 q-dependence of q-deformed potentials.(a)q-deformed Rosen-Morse,(b)q-deformed Pöschl-Teller potentials,which are drawn with parameters a=−1,b=1 and a=−1,b=0,respectively for q values varied in the set of{0.5,1,2}.

3.1 Dark Soliton Solutions

One can easily show that tanhq(x)is also a solution of Eq.(7).This nice property ofq-deformed dark soliton allows us to obtain a first order perturbation solution by rewritingψ0(x)=tanhq(Ax)and potentialU(x)in terms of exponential functions and calculating integrals in Eq.(16).The integration gives first order perturbation solution of the wavefunction as the following,

3.2 Bright Soliton Solutions

It is well known that under attractive interaction whereg<0,a bright soliton solution,ψ0(x)=sech(x)satisfies Gross-Pitaevskii equation Eq.(1).This result can be obtained by proposing a different stationary solution to Eq.(1)as the following,

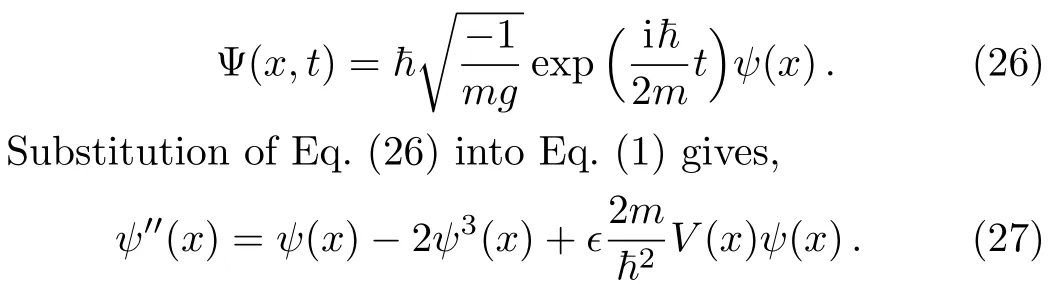
De fining a new scaled potential asU(x)=2mV(x)/~2,taking the limit of limϵ→0and lowering the degree of the derivation will give the first order ordinary differential equation,which is satisfied by the bright soliton ground state wavefunction.

Applying the same steps in Subsec.3.1 one gets a perturbative solution for a bright soliton as the following,

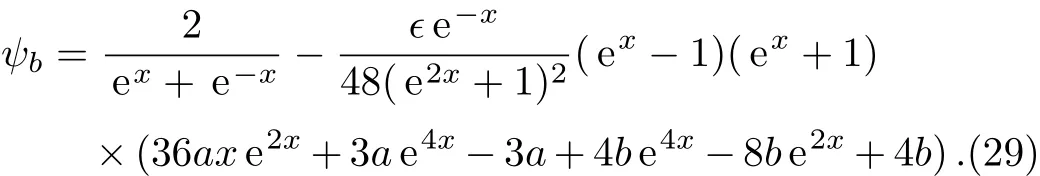
Unfortunatelyq-deformed sechq(x)function does not satisfy Eq.(28),therefore we have only investigated the special case ofq=1.

4 Results and Discussion

In order to understand the localization behavior of the single particle wavefunction,the spatial dependence of the probability distribution is investigated.The probability distribution is found by taking the norm-square of the wavefunction whereϵparameter was kept constant in dark and bright solition solutions and taken as 0.1.In the dark soliton case,underq-deformed Rosen-Morse potential whenq=0.5, first order perturbation of the ground state gives a two-soliton solution.On the other hand atq=1,2 values,the solutions become one-soliton in character as seen in from Fig.2(a).

q-deformed Pöschl-Teller potential has a differentqdependence thanq-deformed Rosen-Morse potential.For allqvalues greater than zero two-soliton solutions are found as seen from Fig.2(b).The asymmetry resulting from theq-deformation of the potentials are reflected to probability distributions as seen in Figs.2(a)and 2(b).Mainlyq-deformation causes a spatial shift in the probability distribution.

When compared to dark soliton solutions,bright ones are respectively sharp and single.The amplitude parameterain the potentials affects the shape of the soliton but does not have any effect on the amplitude of the probability distribution under Rosen-Morse and Pöschl-Teller potentials as seen in Figs.3(a)and 3(b),respectively.

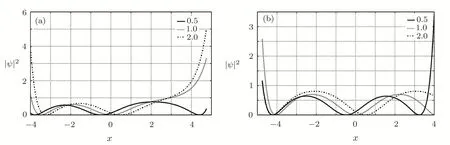
Fig.2 Dark soliton solutions under(a)q-deformed Rosen-Morse potential,(b)q-deformed Pöschl-Teller potential with parameters a=−1,b=1 and a=−1,b=0,respectively for q values varied in the set of{0.5,1,2}.

Fig.3 Bright soliton solutions under(a)Rosen-Morse potential,(b)Pöschl-Teller potential with parameters q=1,b=1 and q=1,b=0,respectively for a values varied in the set of{−0.5,−1,−2}.

5 Conclusions

As a conclusion,in this work Bose-Einstein condensation of the interacting bosonic particles under variousq-deformed potentials is investigated by solving Gross-Pitaevskii equation within a perturbation method.Generalq-dependent dark soliton solutions are found forqdeformed Rosen-Morse andq-deformed Pöschl-Teller potentials.On the other hand,we show that aq-deformed bright soliton does not provide a solution.Therefore,spatial manipulation of BEC might be possible for dark solitons under the investigated potentials,whereas for bright ones it might be impossible.Due to the Dirac-Delta function like behaviour of the Eckart type potential we have not found numerically stable solutions by applying pertur-bation method.Theoretically,it can be speculated that if one can experimentally manage andq-deform the confi ning potentials,than one can spatially manipulate the BEC easily by changing theqparameter.

[1]W.Ketterle and N.J.van Druten,Phys.Rev.A 54(1996)656.

[2]F.Dalfovo,S.Giorgini,L.P.Pitaevskii,et al.,Rev.Mod.Phys.71(1999)463.

[3]W.Ketterle,Chem.Phys.Chem.3(2002)736.

[4]S.Rajendran,P.Muruganandam,and M.Lakshmanan,Physica D 239(2010)366.

[5]R.Yamazaki,S.Taie,S.Sugawa,et al.,Phys.Rev.Lett.105(2010)1.

[6]L.Salasnich,A.Parola,and L.Reatto,Phys.Rev.A 65(2002)043614.

[7]L.Salasnich,A.Parola,and L.Reatto,J.Phys.B:At.Mol.Opt.Phys.35(2002)3205.

[8]E.Kengne,X.X.Liu,B.A.Malomed,et al.,J.Math.Phys.49(2008)23503.

[9]M.Ma and Z.Huang,Appl.Math.Lett.26(2013)718.

[10]M.Ma,C.Dang,and Z.Huang,Appl.Math.Comput.273(2016)383.

[11]L.Salasnich,A.Parola,and L.Reatto,Phys.Rev.A 59(1999)15.

[12]S.K.Adhikari,Phys.Rev.A 69(2004)063613.

[13]Y.P.Chen,J.Hitchcock,D.Dries,et al.,Phys.Rev.A 77(2008)033632.

[14]S.Inouye,T.Pfau,S.Gupta,et al.,Nature(London)402(1999)641.

[15]M.Kozuma,Y.Suzuki,Y.Torii,et al.,Science 286(1999)2309.

[16]S.Inouye,T.Pfau,S.Gupta,et al.,Conference on Quantum Electronics and Laser Science(QELS)—Technical Digest Series 228(2000)229.

[17]S.Dettmer,D.Hellweg,P.Ryytty,et al.,Phys.Rev.Lett.87(2001)160406.

[18]Y.B.Ovchinnikov,J.H.Müller,M.R.Doery,et al.,Phys.Rev.Lett.83(1999)284.

[19]V.Bagnato,D.E.Pritchard,and D.Kleppner,Phys.Rev.A 35(1987)4354.

[20]K.Mallory and R.A.Van Gorder,Phys.Rev.E 88(2013)013205.

[21]P.A.Ruprecht,M.J.Holland,K.Burnett,et al.,Phys.Rev.A 51(1995)4704.

[22]S.L.Chang,C.S.Chien,and B.W.Jeng,J.Comput.Phys.226(2007)104.

[23]L.Pitaevskii and S.Stringari,Bose-Einstein Condensation,Clarendon,Oxford(2013).

[24]A.Arai,J.Math.Anal.Appl.158(1991)63.

[25]A.Arai,J.Phys.A 34(2001)4281.

[26]S.Chaturvedi and V.Srinivasan,Phys.Rev.A 44(1991)8020.

[27]J.Z.Zhang,Phys.Lett.B 440(1998)66.

[28]V.V.Eremin and A.A.Meldianov,Theor.Math.Phys.147(2006)709.

[29]J.Z.Zhang,Phys.Lett.A 262(1999)125.

[30]A.J.Macfarlane,J.Phys.A 22(1989)4581.

[31]X.M.Liu and C.Quesne,Phys.Lett.A 317(2003)210.

[32]R.Parthasarathy and R.Sridhar,Phys.Lett.305(2002)105.

[33]R.J.Finkelstein,Lett.Math.Phys.49(1999)105.

[34]S.Alavi and A.Rouhani,Phys.Lett.A 320 2004 327.

[35]R.K.Gupta and I.L.Cooper,J.Chem.Phys.102(1995)3123.

[36]D.Bonatsos,C.Daskaloyannis,and P.Kolokotronis,J.Chem.Phys.106(1997)605.

[37]Q.J.Zeng,Z.Cheng,and J.H.Yuan,Physica A 391(2012)563.

[38]A.Dobrogowska,Appl.Math.Lett.26(2013)769.

[39]M.S.Abdalla,H.Eleuch,and T.Barakat,Rep.Math.Phys.71(2013)217.

[40]M.Sebawe Abdalla and H.Eleuch,J.Appl.Phys.115(2014)234906.

[41]B.J.Falaye,K.J.Oyewumi,and M.Abbas,Chin.Phys.B 22(2013)110301.