Entanglement Swapping in the Presence of White and Color Noise
2018-05-23IvanDotsenkoandKorobka
Ivan S.Dotsenko and R.Korobka
Taras Shevchenko National University of Kyiv,Kyiv,Ukraine
1 Introduction
The entanglement phenomenon gradually became an object of intensive research after Aspect’s group[1]had convincingly(through experiments)proven the violation of Bell’s inequalities by the entangled states.
It became clear with time that entanglement is a new resource of nature,which can be created,preserved,distributed,concentrated and transmitted over a distance.Nowadays,entanglement is actually being created and processed in many physics laboratories.Entangled states carriers are quite versatile,it could be photons,ions,atoms,molecules,crystals and more.Discovering the role of entangled states stimulated emergence of new areas in modern physics,such as quantum computing,quantum cryptography and quantum communication.
As it is well known,an arbitrary state of any single qubit can always be represented as a vector in twodimensional Hilbert space:

with normalization
The principal difference between qubits and classical bits is a possibility of existence of states in a form of superposition of basis vectors.
The state of two-qubit system is described by a vector in a 4-dimensional Hilbert space,which is the tensor product of Hilbert spaces of individual qubits.The most common bases in this space are computational(standard)basis in the form of a tensor product of relevant basis states of individual qubits:


It is customary to call Bell states the EPR pairs,because that type of states is discussed in the Einstein,Podolsky,Rosen work.[2]All Bell(2)states are entangled,because they cannot be represented in a form of a product of individual qubits vector states.
The most interesting and unusual phenomenon,based on entanglement,is a quantum teleportation and entanglement swapping(ES).First,the scheme(protocol)of unknown qubit state teleportation was proposed in Ref.[3](Bennettet al.).Detailed reference to the original work on quantum teleportation can be found,for example in Refs.[4]and[5].
For some time it was believed that entangled system state,consisting of two or more quantum subsystems(particles,photons),is created only during their simultaneous birth in a single event from a common source,or as a result of subsystems interaction.However,in 1993[6](Zukowskiet al.)a protocol was proposed,as a result of which the quantum correlations(entanglement)could be created between the particles that may be located at great distance from each other,and which did not share a common history.This process is called the entanglement swapping(ES).
A paper by Zukowskiet al.for a short time was widely appraised among scholars.Duret al.[7]developed a quantum communication protocol for long distances using quantum repeaters with ES as their element.Xueet al.[8]proposed ES scheme,which is based on three-particle GHZ state for the needs of quantum cryptography.The entan-glement swapping process is sometimes called the entanglement teleportation or teleportation of entangled states.Tsaiet al.[9]used GHZ-like state for teleportation of pure EPR state.At the same time in addition to theoretical developments of teleportation protocols and ES,the real experiments[10−13]are gradually improved in physics laboratories.For a correct assessment of real possibilities to transfer quantum state over long distances,all factors that affect the signal quality at all stages of its formation and passage through channels of communication should be taken into consideration.A detailed discussion of this topic can be found at Ref.[14].To study the overall infl uence of all these factors,it is necessary,in our point of view,to display full understanding of physical processes in each single element of the communication channel.
Entanglement swapping is used in real elements of quantum communication channels,such as quantum repeaters.Quantum states at the input of these elements always have some level of noise.Motivation of this research is to get to know how type and level of noise at the input of such elements will affect on the quality of output state.The aim of this work is a theoretical study of the e ff ect made by the presence of noises in initially created entangled states on the final state obtained as a result of entanglement swapping operation.
For better explanation of the gist of this paper we remind the essence of the entanglement swapping phenomenon that can be illustrated by a specific example.
Let two sources independently form one pair of qubits each in one of the entangled EPR states of Eq.(2).For example,in the experiment[10]short UV pulses were fl own through nonlinear BBO-crystal(β-BaB2O4).As a result of parametric down-conversion type II,pairs of photons were formed in polarizingly entangled Bell state|Ψ−>.Due to independent formation of two such entangled pairs,four-qubit system state is represented as a tensor product of individual qubit-pair states(number of qubits marked by symbols):

A pair of qubits(photons)2 and 3 further undergoes a projective measurement in Bell basis(2).A measuring device is adjusted in such a way,so in compliance with the scheme of signal coincidences,an event emerges from detectors,when a pair of photons 2 and 3 is in state
This operation is called an incomplete projective measurement.Mathematically,the operation is considered as a projection of the state>on the state
By regrouping summands,the state vector>can be written as:

that is,a pair of qubits which numbered 1 and 4 is in the same stateas previously prepared two-pair states of qubits 1 and 2 or qubits 3 and 4.
Since the operation of projection on a particular state is incomplete von Neumann measurement,so as a result of projection we obtain state vector,which is nonnormalized.In this very case,multiple repeating of the operation preparing>state and subsequent projection on>theoretically,on average,only one event out of 4 attempts to provide the desired e ff ect>.But after the event was recorded,the state vector is considered normalized to one.Basically one can also consider complete measurement of von Neumann in the Bell basis.Then,as a result of each act ES,particles 1 and 4 are in one of four possible states:with probability 1/4 for each state.Further use of LOCC can convert these states,so with a probabilityw=1 the final state will beNote that preliminary prepared qubit couples were created independently from each other and particles 1 and 4 by no means interacted with each other.
ES process can be represented as a simple scheme(Fig.1).[10]
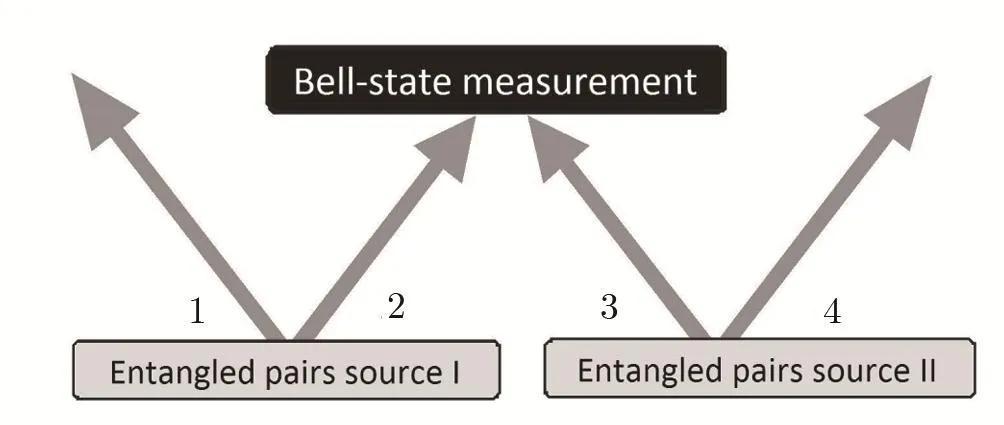
Fig.1 Scheme of entanglement swapping process implementation.
Note that the entanglement of 1 and 4 qubits occurs just at the moment of projecting on the state>.Theoretically,qubits 1 and 4 in this connection can be at any distance from each other.
It is considered in the analyzed example,that both qubit pairs are prepared in apureBell’s stateand as a result of ES,we obtain the samepureentangled state of qubits 1 and 4,which can be located at a distance from the initially prepared pairs of qubits.In quantum information science the pure states are sometimes called coherent states because unlike the mixed states,they can be represented as a coherent superposition of basis states.
In this paper the process of entanglement swapping is considered under condition of presence of different types of noise in initially prepared entangled states.
For a comparative analysis of states of initially prepared and final pairs of qubits,below we use known characteristics of entanglement:concurrence(C),tangle(τ),entanglement of formation(Ef);characteristics of degree of mixture:von Neumann entropy of two-qubit state condition(E),purity(Tr(ρ2)),linear entropySL;degree of coincidence(or differences)of initial and final states:trace metricδand fidelityF.
For the initial state of two-qubit system and for states,produced by ES we will calculate next sequence of characteristics(points(i)–(ix)will be calculated in next chapters for initial state,and(x)–(xi)as comparative characteristics between initial and final states):
(i)Matrix(spin flipped state)by converting:

whereλρinare eigenvalues of matrix density of each of the initially prepared qubit pairs,λρfinare eigenvalues of matrix density obtained by the operation ES.Ifδis a measure of the distance between two states,so the parameter

Let us consider the phenomenon of entanglement swapping in a case where each of the two qubit pairs is formed in a mixed state.
2 Entanglement Swapping in the Case of Presence of White Noise in the Initial State
Let us add all the basic states with the same weight coefficients to the pure state>in a mixture.Density operator of such a state is called the Werner state[15]and represented as:

Supposing that qubit pairs with numbers(1,2)and(3,4)are prepared independently,the density operator of two pairs of qubits system is represented as tensor product of states(14):

in Bell’s basis,wherep1andp2are pure state weight coefficients with respect to the first and the second initial qubit pairs(pairs of particles 1,2 and 3,4).Hence,
(i)If one of the qubit pairs is prepared in a pure state(p1=1 orp2=1),so the density matrixρ14duplicates a density matrix of the second pair of qubits prepared in the mixed initial state.
(ii)If both qubit pairs are prepared in the mixed state,then the resulting state of qubits pair 1 and 4 will be noisier than the state of each of the initially prepared pairs.
Let us consider the casep1=p2=pin detail.Then the density operator of the final state of qubits for ES operation will be similar to Eq.(14):

Thus,is obtained from Eq.(14)by replacement ofthe density matrix of this state in the computational and in Bell’s basis looks like Eqs.(15)and(16)after replacingin them.That means that the states of initial and final qubits pairs are similar with accuracy up to the replacement mentioned above.Sincep∈[0,1],thenand,thus,,which indicates an increase in admixture of white noise as a result of transition from the initial to the final state.
Comparison of the von Neumann entropy values for each of the initial and final pairs of qubits gives a clear demonstration of an increase in admixture of white noise.Figure 2 reproduces the entropy dependence on the parameterpfor both systems.The solid-line curve corresponds to the entropy of pair of 1 and 4 qubits,a dashedline curve corresponds to the entropy of each of the initial qubit pairs.

Fig.2 Dependence of the von Neumann entropy on parameter p.Curve 1 for each initial qubit pairs(Werner state),curve 2 for qubit pair,obtained by ES procedure.
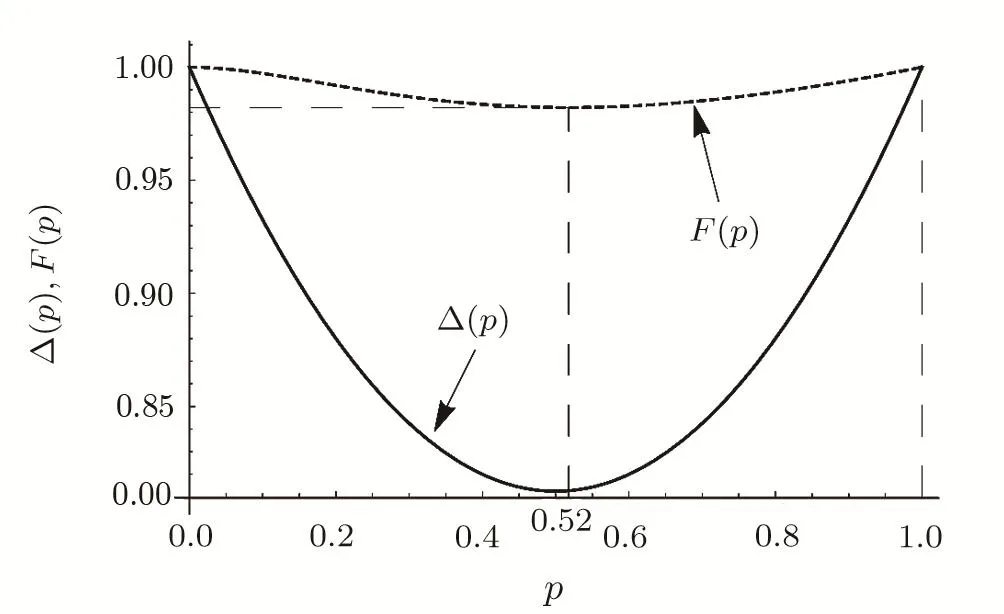
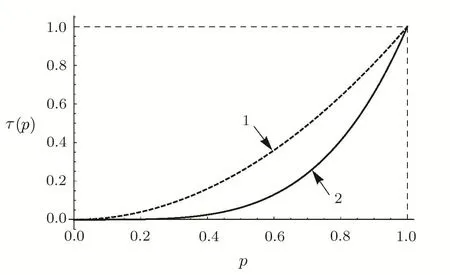
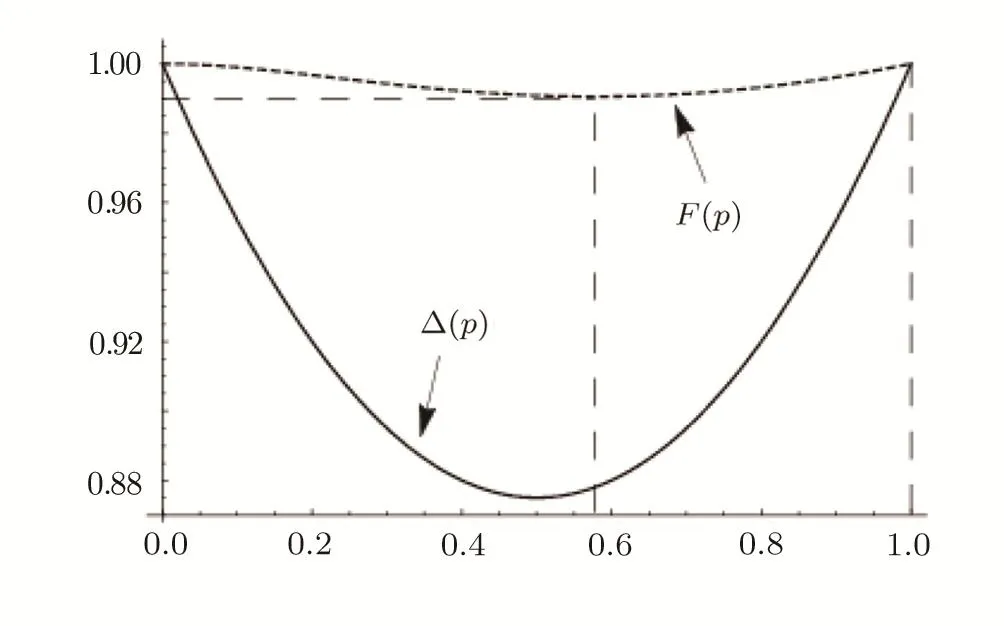
The fi gure shows that the entropy of the final pair of qubits for 0 According to the Perez-Gorodetsky criterion[16−17]the positive partially transposed(PPT)density matrix is necessary and sufficient condition for the absence of entanglement in the two-qubit systems.Violation of this condition indicates the presence of entanglement. Partially transposed density matrix of initial state(15)in the standard basis is presented as: Let us find the range of parameterp,which provides the entanglement of initial qubits pair.After diagonalization of Eq.(20)we obtained: The eigenvalues of the matrix(20)λ1=λ2=λ3=(1+p)/4 forp∈[0,1]are nonnegative.The only eigenvalue that can take negative values isλ4: For Werner state this result is well known and was first presented in Ref.[3]. The range ofp,for which final state is entangled,is defined by similarity ofp→p2between initial and final pairs: Thus,the initial entangled states of two qubit pairs withform non-entangled state after entanglement swapping operation,i.e.the entanglement property is lost. Now let us consistently follow point-by-point the steps(i)–(xi)mentioned above in Sec.1.Analytical expressions for points(i)–(ix)are presented only for the characteristics of initial qubits states(Werner states).The corresponding values for the final states could be obtained by simple replacingp→p2.Other characteristics((x)and(xi))are obtained using initial and final states.Comparison of corresponding characteristics of the initial and final states was conducted by means of graphs.In accordance with points(i)–(xi)we consistently find: (viii)Linear entropy(9): (ix)Von Neumann entropy(10),which can be obtained by taking the eigenvalues of the matrixρ(16): We remind that similar characteristics of the final state are obtained by replacing ofp→p2in points(i)–(ix).Let us indicate the value of similarity(or difference)of characteristics of initial and final qubits states. (x)Trace metricδ(11)and parameter∆ =1−δ: forp=0 andp=1→δ=0:white noise becomes white noise and pure state becomes pure state.The final state is the least similar to the original ifp=1/2 and∆min=13/16. (xi)Fidelity(13) This similarity measure has its minimum forp≈0.52,Fmin≈0.98.It follows thence that for allp∈[0,1] fidelity value differs little fromF=1.0,thus indicating a weak sensitivity of the given characteristics to a state change as a result of ES.The parameter∆turns out to be more sensitive measure. Fig.3 “Tangle” dependence of state qubits pairs on parameter p.Curve 1 is for initially prepared state of qubits pair(Werner state),curve 2 for qubits pair state obtained as a result of the ES operation. Figures 3–5 show corresponding dependencies “tangle”,“entanglement of formation”,linear entropy on the parameterpfor the state of initially prepared qubits pairs(dashed-line curve)and a pair of qubits state produced by ES(solid-line curve).Figure 6 depicts dependencies graphs∆(p)andF(p),which characterize the similarity between the initial and final states. Fig.4 Dependence “entanglement of formation” of qubits pair state on parameter p.Curve 1 is for initially prepared state of qubits pair(Werner state),curve 2 for qubits pair state obtained as a result of the operation ES. Fig.5 Dependence of linear entropy of qubit pair on parameter p.Curve 1 is for initially prepared state of qubits pair(Werner state),curve 2 for qubits pair state obtained as a result of the operation ES. Fig.6 Dependences of similarity characteristics between initial and final states∆(p)and fi delity F(p)for Eqs.(14)and(18)states,if the white noise is presented in the initial states. Let us now analyze the final state of qubits pair after ES operation in the case of presence of color noise in the initial states. The initial state of each qubits pair(ρ12andρ34)now looks as follows:[18] Hence,it follows that if one of the qubit pairs(e.g.a pair from first and second qubits)is prepared in the pure state(p1=1),then final state density matrixρ14duplicates density matrixρ34of second qubits pair in the initial state. Forp1=p2=pdensity operator of qubits final state can be represented in a similar way to Eq.(23),namely: Since,as it was in previous case,the states of initial and final qubit pairs are similar,then corresponding final state density matrices in the computational and Bell basis can be obtained from Eqs.(24)and(25),following the replacementp→p2. As a result of the operation ES,the share of color noise increases.So farp∈[0,1],andp2≤pthen 1−p2≥1−p.Ifp=0 orp=1 the final state fully duplicates initial state. Figure 7 represents comparative graphs of the von Neumann entropy two-qubit system dependence on the parameterpfor the state of each initially prepared qubit pairs(dashed-line curve)and qubits pair state obtained by means of operation ES(solid-line curve). Fig.7 Dependence of von Neumann entropy on p in the presence of color noise.Curve 1 is for initially prepared states of qubits pairs,curve 2 for qubits pair state obtained as a result of the ES operation. The figure shows that the entropy of the final qubits pair for 0 Let us also indicate that the maximum entropy value(forp=0)equalsSmax=1,while in the previous case(white noise)Smax=2.This difference is quite standable since white noise is the most chaotic state. Reduced density matrix corresponding to the matrices(24)and(25),is proportional to the identity matrix,as well as in the previous case,and therefore von Neumann entropy for the reduced matrix of each qubit from pair does not depend onpand equals 1—the highest possible value for a single qubit. Partially transposed density matrix of the initial state of qubits pair in the standard basis looks as follows: and the eigenvalues of the matrix have the valuesλ1=λ2=1/2,λ3=p/2,λ4=−p/2.Thusλ4<0 for 0 Using the similarity of initial and final states(p→p2),we come to conclusion that pair of qubits 1 and 4 after performing the operation entanglement swapping will also be entangled for any value of the parameterp>0.In this case it is impossible situation when entangled state becomes non-entangled after ES. Below we present the values of characteristics(i)–(ix)only for initially prepared pairs of qubits.The same values for the qubit state pairs obtained by ES operation,are defined by similarityp→p2.Other characteristics((x)and(xi))are obtained using initial and final states.Thus we find: has minimum forp≈0.58,Fmin≈0.99.So,in this case fi delity is not sensitive to operation ES. Figures 8–10 show corresponding dependencies of“tangle”,“entanglement of formation” and linear entropy on the parameterpfor initial and final states. Fig.8 Dependence of“tangle” on p parameter.Curve 1 is for initially prepared states of qubits pairs(color noise),curve 2 for qubits pair state obtained as a result of the ES operation. Fig.9 Dependence of“entanglement of formation” on p parameter.Curve 1 is for initially prepared states of qubits pairs(color noise),curve 2 for qubits pair state obtained as a result of the ES operation. Fig.10 Dependence of linear entropy on p parameter.Curve 1 is for initially prepared states of qubits pairs(color noise),curve 2 for qubits pair state obtained as a result of the ES operation. Figure 11 depicts dependencies of∆andFonp.From Eqs.(29)and(30)it immediately follows that betweenSLandτthere is a simple dependenceSL=2(1−τ)/3,which is the same for both the initial and final states. Fig.11 Dependence of∆(p)and F(p)for Eqs.(23)and(26)states. Let us assume now that there is simultaneous presence of white and color noise in the initial states of two pairs of qubits. State of initially prepared pairs in this case is defined by density operator:[19] wherea1=1−(p1+r1)(p2+r2),a2=1+(p1+r1)(p2+r2),a3=−2p1p2ncomputational basis,and Let us analyze now the redistributionas a result of the ES process. Forp=1(thenr=0 andq=0)we obtain:Thus,as mentioned above,the initial pure state becomes a pure state. Forp=0 andSince,then a share of white noise is increased only by reducing the color noise. Forp=0,r=0(thenq=1),i.e.the state does not change. If in the initial state(31)share of pure state equals to the share of white noise:then,as a result of ES the share of color noise does not change,the increase of white noise occurs only by reducing the share of pure state.Actually: Then it is clear that forp Forp>q(p>(1−r)/2)the color and white noises increase by reducing the share of pure state. Density matrix of state(34)in the standard basis has the form where,and in Bell basis where For anyp∈[0,1]andr∈[0,1−p]von Neumann entropy valuesSfin(p,r)of final state will exceed the entropy valueSin(p,r)of each initial states.The biggest difference of entropies∆S≈0.4 is observed ifp≈0.72,r≈0.15. Reduced density matrices corresponding to the matrices(32)and(36),will be proportional to the identity matrix,as in the previous case,and therefore von Neumann entropy for state of each qubit equals 1 and does not depend onpandr. Let us find a range ofpandrwhen a state of each initially prepared pairs is entangled.Partially transposed density matrix for the state of each initially prepared pairs in standard basis looks as follows: Due to conditions(p∈[0,1],r∈[0,1−p])only one eigenvalue of partially transposed matrix may be less than zero,namely: This result was obtained earlier in the paper.[19] Let us now find the range of valuespandr,for which the final states are entangled.Such a range one can express by means of inequality,which results from Eqs.(35)and(38): Figure 12 shows ranges of parameter valuespandr,in which the initial and final system are or not entangled. The graph shows that there is a range of parameter values(in Fig.12 denoted as 2),in which the state of each initially prepared pair is entangled,but a pair state obtained as a result of operation ES,is unentangled.Thus,the ES process makes possible a situation when the final state of qubits 1 and 4,as a result of noises influence,will not be entangled,while the initial qubit pairs are entangled. Fig.12 Ranges of parameters p and r:1 is for initial and final states are nentangled(separable),2 for initial state is entangled, final is unentangled,3 for initial and final states are entangled. Let us now give initial state characteristics according to points(i)–(ix).Corresponding characteristics for final state could be found from below values for initial state,by applying designations from Eq.(35)Two last points(x)–(xi)are calculated using initial and final states.Thus we find: (ix) von Neumann entropy(10),which can be obtained by the eigenvalues of the matrixρfrom Eq.(33): wheredifferent values ofδfor differentδ1are caused by absolute values of differences between eigenvalues of initial and final state matrices.Parameter∆(p,r)may be obtained by Eq.(12)as 1−δ(p,r).The minimum value∆(p,r)obtained forp=0.5,r=0,∆min=13/16; (xi)ParameterF(13): This measure of similarity has minimum forp≈0.52,r=0,Fmin≈0.98. (i) If one of the qubits pair is prepared in a pure state(p1=1,orp2=1),then density matrix of qubits pairρ14,that is obtained by the ES process,duplicates density matrix of the second pair of qubits,prepared in a mixed state.If both pairs of qubits are prepared in a mixed state,then the final state of qubits pair 1 and 4 will be noisier than a state of each initially prepared pair that leads to an increase in von Neumann entropy of qubits pair. (ii)Entanglement swapping produces various schemes of white and color noise redistribution.It depends on ratio between white and color noise in the initial states.(Detailed description of different schemes of redistribution see above in the text). (iii)In the entanglement swapping process for some range of parameters valuespandroccur total decoherentization of state–entangled state becomes an unentangled one. (iv)Results could be helpful for experiments regarding [1]A.Aspect,J.Dalibard,and G.Roger,Phys.Rev.Lett.49(1982)1804. [2]A.Einstein,B.Podolsky,and N.Rosen,Phys.Rev.47(1935)777. [3]C.H.Bennett,G.Brassard,C.Crepeau,et al.,Phys.Rev.Lett.70(1993)1895. [4]R.Horodecki,P.Horodecki,M.Horodecki,and K.Horodecki,Rev.Mod.Phys.81(2009)865. [5]C.Y.Hu and J.G.Rarity,Phys.Rev.B 83(2011)115303. [6]M.Zukowski,A.Zeilinger,M.A.Horne,and A.K.Ekert,Phys.Rev.Lett.71(1993)4287. [7]W.Dur,H.J.Briegel,J.I.Cirac,and P.Zoller,Phys.Rev.A 59(1999)169. [8]Z.Y.Xue,Y.M.Yi,and Z.L.Cao,Chin.Phys.15(2006)1421. [9]C.W.Tsai and T.Hwang,Phys.Scr.84(2011)045006.entanglement swapping as conditions for prepared quantum entangled states,to obtain result state as also entangled.It could be used for con fi guration of quantum communication channels devices such as quantum repeaters. [10]J.W.Pan,D.Bouwmeester,H.Weinfurter,and A.Zeilinger,Phys.Rev.Lett.80(1998)3891. [11]T.Jennewein,G.Weihs,J.W.Pan,and A.Zeilinger,Phys.Rev.Lett.88(2001)017903. [12]H.de Riedmatten,I.Marcikic,J.A.W.van Houwelingen,et al.,Phys.Rev.A 71(2005)050302(R). [13]C.Y.Lu,T.Yang,and J.W.Pan,Phys.Rev.Lett.103(2009)020501. [14]A.Scherer,R.B.Howard,B.C.Sanders,and W.Tittel,Phys.Rev.A 80(2009)062310. [15]R.F.Werner,Phys.Rev.A 40(1989b)4277. [16]A.Peres,Phys.Rev.Lett.77(1996b)1413. [17]M.Horodecki,P.Horodecki,and R.Horodecki,Phys.Lett.A 223(1996)1. [18]A.Cabello,A.Feito,and A.Lamas-Linares,Phys.Rev.A.72(2005)052112. [19]I.S.Dotsenko and V.G.Voronov,Opt.Commun.282(2009)2889.
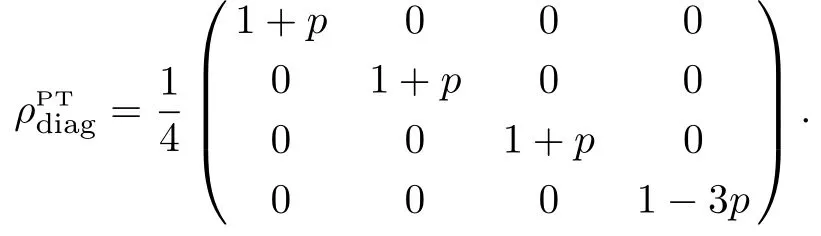










3 Entanglement Swapping in the Case of Presence of Color Noise in the Initial States







4 Entanglement Swapping in the Case of Presence of White and Color Noise in the Initial States




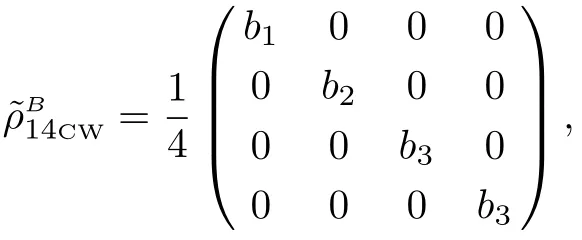






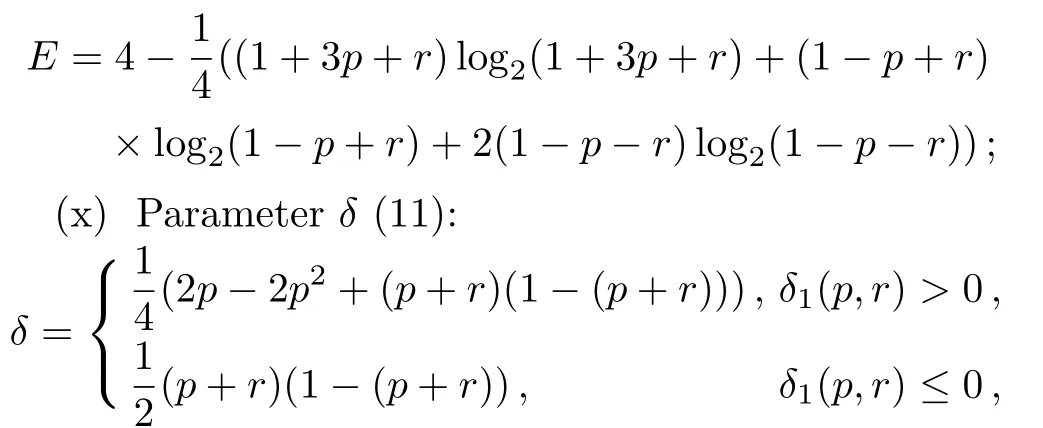

5 Conclusions
杂志排行
Communications in Theoretical Physics的其它文章
- Parameterization of Nuclear Hulthén Potential for Nucleus-Nucleus Elastic Scattering
- Dirac Quasinormal Modes of Static f(R)de Sitter Black Holes∗
- Bilinear Forms and Soliton Solutions for the Reduced Maxwell-Bloch Equations with Variable Coefficients in Nonlinear Optics∗
- Scalar Hidden-Charm Tetraquark States with QCD Sum Rules∗
- Thermodynamic Geometry of Charged AdS Black Hole Surrounded by Quintessence∗
- Phase Transition and Physical Properties of InS∗
