Nodal Topological Phases in s-wave Super fluid of Ultracold Fermionic Gases∗

Bei-Bing Huang(黄备兵) and Xiao-Sen Yang(杨孝森)

1Department of Physics,Yancheng Institute of Technology,Yancheng 224051,China

2Department of Physics,Jiangsu University,Zhenjiang 212013,China

1 Introduction

The spin-orbit coupling(SOC)can be artificially operated for neutral ultracold atom gases in the continuum[1−4]and/or optical lattices[5]by using optical Raman transitions,which has pushed forward cold atom physics into a brand new era.In the continuum the experimentally obtainable SOC was generally one-dimensional(1D)and always accompanied by the Zeeman field along the same direction as the SOC.A recent experiment[5]for the first time successfully realized a controllable crossover between two-dimensional(2D)and 1D SOC in optical lattices.In this featured scheme the Zeeman field along the direction of SOC is avoided,irrespectively of 1D or 2D SOC.

The Zeeman field along the direction of SOC influentially affects the ground state of many-body system.When the attractive s-wave interaction among fermions is assumed,this Zeeman field will lead to the ground state to be Fulde-Ferrell-Larkin-Ovchinnikov(FFLO)state,[6−19]and under this circumstances the sole symmetry of the system is the particle-hole symmetry(PHS)inherent in superconducting/super fluid systems.From the viewpoint of symmetry protection,PHS maps the momentumkinto−kand only protects the gapped topological phases.Without this Zeeman field,the many-body ground state is Bardeen-Cooper-Schrie ff er(BCS)state and possesses the chiral symmetry for the systems with 1D SOC.The chiral symmetry maps the momentumkinto itself and can protect some important topological super fluid phases,including gapped and gapless topological phases.Thus in the optical lattice scheme,the absence of the Zeeman field along the same direction as the SOC enriches the manybody phases of the system.

Generally in the process of generating SOC,an effective Zeeman field coming from two-photon detuning of Raman lasers always exists.[1−5]In this paper we study the ground states of the three-dimensional(3D)cold fermionic gases in cubic optical lattices with 1D SOC alongxdirection and Zeeman field alongzdirection.At the BCS mean- field level,the self-consistent calculations indicate that the system can be gapless super fluid with topologically protected nodal lines.We define two topological invariants to characterize the stability of nodal lines.The topological super fluid with nodal lines can be regarded as the super fluid counterpart of nodal line semimetal widely studied in the solid state materials Ca3P2,[20]SrIrO3,[21]PbTaSe2[22]and stable 3D carbon allotrope.[23−24]A theoretical model for the nodal line semimetal in the context of cold fer mionic gases has also been suggested.[25]In contrast to 2D gapped D class topological super fluid[26−28]and 3D gapless Weyl super fluid,[15,29−33]the nodal line topological super fluid brings novel dispersionless zeroenergy flat band in a finite region of the surface Brillouin zone(BZ).Experimentally these nodal lines should be detectable through the momentum-resolved radio-frequency spectroscopy.[34−36]

2 Model

The 3D Hamiltonian in the cubic optical lattice we consider is

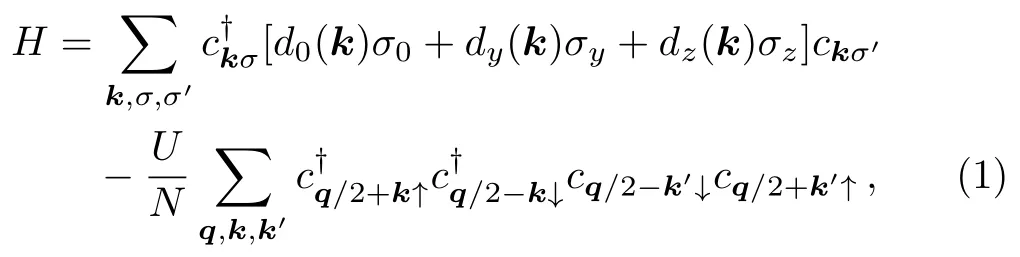
whereckσis fermion’s destruction operator andare the hopping terms in optical lattices alongx,y,zdirections andU,Nandarespectively are the chemical potential,the strength of contact attractive interaction,the number of unit cell and the lattice constant.The 3D optical lattice is generated by three mutually orthogonal laser standing waves at a wavelength ofλ=2aand a mutual frequency difference to avoid interference between standing waves.The 1D SOC with strengthαin thexdirection can be achieved by choosing the Rabi frequencies of the corresponding Raman lasers as Ω1(x)= Ω0cos(πx/2a)andΩ2(x)= Ω0sin(πx/2a),which respectively can be realized with a pair of plane-wave lasersandas shown in Fig.1.hzoriginates from two-photon detuning,acting as the Zeeman field alongzdirection.For the detailed derivation of Hamiltonian(1),please refer to Ref.[25].In addition to produce the required SOC,such two Raman fields also contribute diagonal potentialwith periodicity 2ato spin-up(spin-down)fermions.These diagonal potentials have been neglected in Ref.[25].In this paper,in order to minimize the roles of these diagonal potentials,we assume that the optical lattice alongxdirection is very deep,so thattxis expected to be very small.Below we seta=1.

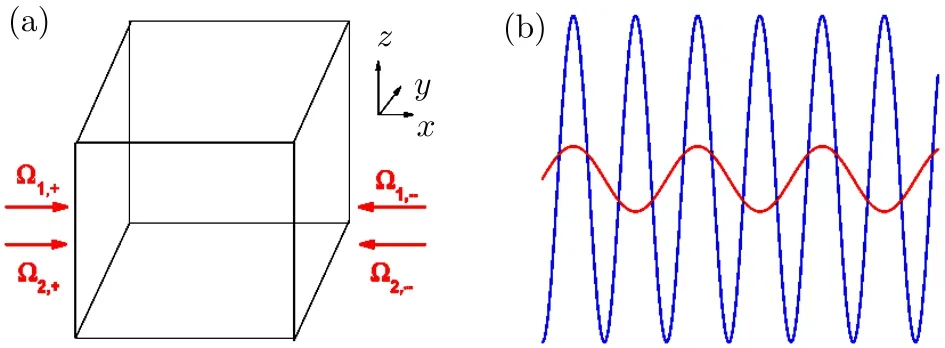
Fig.1 (Color on line)(a)The cubic optical lattice system and laser con figuration for producing 1D SOC along x direction.(b)The schematic plots for the optical lattice potential(blue line)along x direction and Raman potential(red line)proportional to Ω1(x)Ω2(x).

At the level of BCS mean- field approximation,the Hamiltonian can be written in a matrix form

and is assumed to be real throughout this work.It is then straightforward to get the thermodynamic potential at zero temperature

where the quasi particle’s excitation spectra

are the positive eigenvalues of the matrixHBdG(k).The order parameter can be self-consistently decided by requiring

After deciding the order parameter,some properties of the system can be deduced from the excitation spectrumE−(k).It is easily found thatE−(k)can become gapless atkx=0 plane when

These gapless points constitute the gapless nodal lines.Depending on the number of gapless lines atkx=0 andkx=πplanes,the system can show many different phases as shown below.

The existence of nodal lines in 3D can be easily understood by observing the chiral symmetry ofsatisfies PHSand time-reversal symmetry(TRS).Combining TRS and PHS yields the chiral symmetryIn the basis of diagonalizing chiral operatorHBdG(k)can be rearranged into the non-diagonal block form

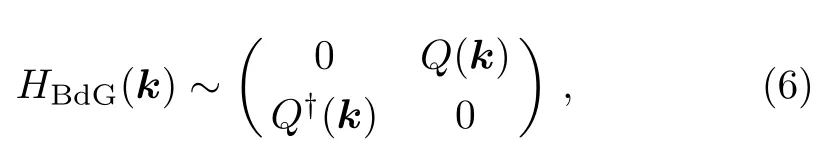
thus the nodal points are specified by two real equations Re[Det(Q)]=Im[Det(Q)]=0.Every real equation defines a curved surface in 3D Brillouin zone(BZ),so that the nodal lines correspond to the intersecting lines of these two curved surfaces.

To characterize the topological properties of these nodal lines,we introduce two different topological invariants.Since the chiral symmetry is satisfied at any given point in the BZ,for any a closed loopLin BZ not intersecting the nodal lines,it is gapped and belongs to symmetry class AIII,and its topological features are described by the 1D winding number[37−40]

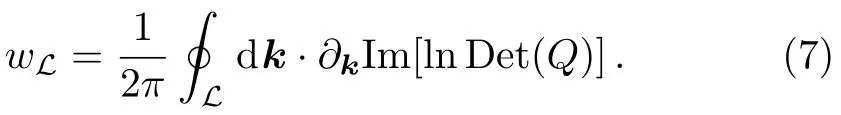
WhenLis chosen to encircle a nodal line,wLdetermines its topological stability.

The topological protection of a nodal line in 3D can also be characterized by the Berry phaseγ[41]defined for above mentioned closed loopL

3 Phase Diagram and Topological Properties

Sincehzandµcan be tuned independently by controlling respectively the two-photon detuning and particle number,we map out self-consistently the phase diagram of the system on theµ-hzplane for the fixed strengths of interaction and SOC.The another advantage of choosing the chemical potential as free parameter is that we can qualitatively deduce the phase structure of the system in the trap potential under the local density approximation from the phase diagram in the uniform lattice.Without loss of generality,we chooseas the unit of energy andU/t=3.0 andα/t=2.0.In order to distinguish different phases,we use four ordered integersto label them.The integerindicates the number of the nodal lines atplane.Whenthe system has the four-fold rotation symmetry and every nodal line atplane will encircle eitherWe use the integerto further point out the number of nodal lines encircling theplane.For the gapped phase we use the notation(0,0)to label it.

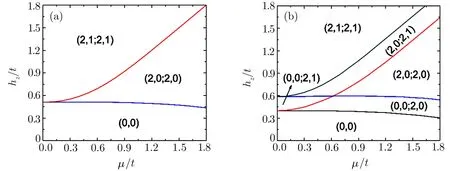
Fig.2 The numerically self-consistent phase diagrams for different parameter tx/t=0(a)and tx/t=0.08(b)as the function ofµ and hz.In order to distinguish different phases,we use four ordered integers(n0,n00;nπ,nπ0)to label them.The integer n0(nπ)and n00(nπ0)respectively indicate the total number of the nodal lines and the number encircling the(ky,kz)=(0,0)at kx=0(kx=π)plane.For the gapped phase we use the notation(0,0)to label it.

Figure 2(a)shows the phase diagram of the system fortx=0.There are three qualitatively different classes of super fluid states in the phase diagram:the fully gapped(0,0)state,the nodal super fluid states(2,0;2,0)and(2,1;2,1).The topological structure of phase diagram can be qualitatively understood from Eqs.(4)and(5),which are the same fortx=0.For the fixed chemical potential,the order parameter∆from the self-consistent calculation decreases smoothly with the increase ofhz.Whenhz<∆the nodal lines cannot be defined and the system is gapped.Ifhzis in fi nitesimally larger than∆,we haveAs a result two nodal lines encirclingare created respectively forkx=0 andplanes and the system enters into(2,0;2,0)state. Increasing furtherone of two nodal lines in every plane begins to encircleand(2,1;2,1)state is obtained.Especially for large chemical potential,hzdefining the phase boundary between(2,0;2,0)and(2,1;2,1)phases is also large,so that∆is small and the phase boundary of these two phases is coarsely described byThis expectation is consistent with the numerical phase diagram.

To visualize these nodal line super fluid states,we calculate their corresponding gapless contours in 3D BZ(see Figs.3(a)–3(b)).In principle,one may probe these dispersion spectra experimentally by the momentum resolved radio-frequency spectroscopy,[34−36]from which the topology of the momentum space gapless contours of the various nodal line states can be probed.For(0,0)state,the system is gapped and topologically trivial.While for all other phases,we have numerically calculated the two topological invariants(7)and(8).The results suggestwL=±1,and they are topologically nontrivial.

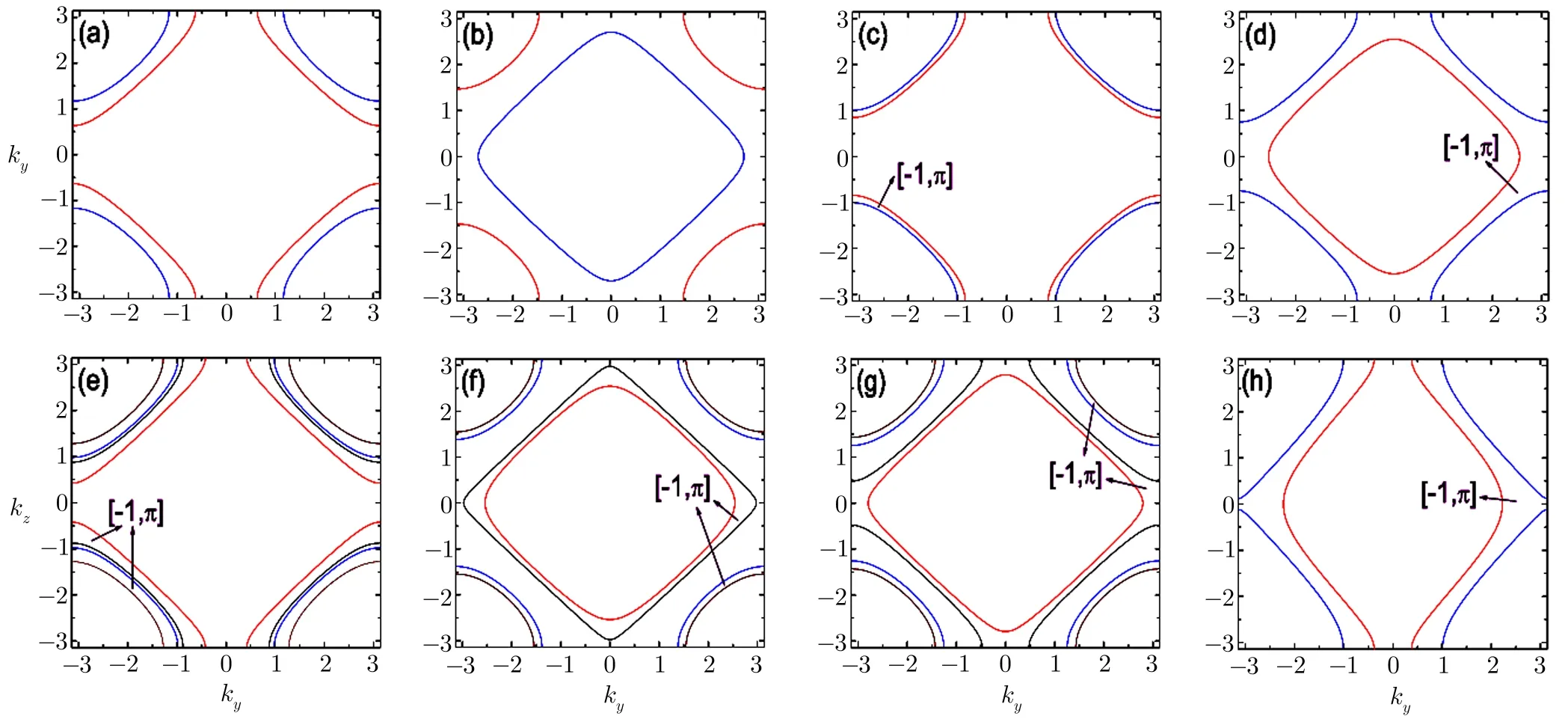
Fig.3 The gapless contours for different nodal line super fluid phases,viewed along the x direction.(a)and(e),(b)and(f),(c),(d)and(g)correspond to phases(2,0;2,0),(2,1;2,1),(0,0;2,0),(0,0;2,1),(2,0;2,1).The parameters areµ/t=0.8,hz/t=0.6 in(a)and(e),µ/t=0.8,hz/t=1.0 in(b)and(f),µ/t=0.8,hz/t=0.4 in(c),µ/t=0.1,hz/t=0.5 in(d),µ/t=0.8,hz/t=0.8 in(g).In(a)and(b)tx=0,while in(c)–(g)tx/t=0.08.The ordered number in purple indicates the momentum-dependent topological invariants w(ky,kz)and γ(ky,kz)in the corresponding regions.For the remaining regions these two invariants are zero.(h)shows a characteristic open nodal line topological super fluid when the anisotropy in y and z is introduced.In(h)tz=t,µ/t=0.1,hz/t=0.5,tx/t=0.08,ty/t=1.3,thus(h)can be obtained from(d)by increasing ty.As a result a closed nodal line becomes open.

In the limit oftx=0,the nodal lines atkx=0 andkx=πplanes are superimposed when viewed along thexdirection,which leads to the absence of zeroenergy surface states inky-kzsurface BZ,although the nodal lines are topologically nontrivial. The absence of the surface states can easily be seized in a dimensional reduction manner.In momentum space consideringky,kzas external parameters,the system consists of a series of 1D subsystems indexed by differentky,kz. Every subsystem has still the chiral symmetry and is gapped as long asky,kzare not consistent with nodal line’s momenta.For the gapped 1D subsystem,we consider the variants of topological invariants(7)andIf these two topological numbers are nonzero,such subsystem is topologically nontrivial.As the function ofky,kz,w(ky,kz),γ(ky,kz)could show discontinuous jumps if the integration path intersects nodal lines.When the boundaries alongxdirection are imposed,the subsystems with nonzero topological numbers will show zero energy edge states.The calculations of momentum-dependent topological invariants indicatew(ky,kz)=γ(ky,kz)=0 and signify the absence of zero-energy surface states.

The absence of zero-energy surface states is caused by the simultaneous gap closing and reopening for 1D subsystem indexed bykyandkzatkx=0 andkx=π.Thus in order to obtain zero-energy states in theky-kzsurface BZ,we must break this coincidence,which can be operated by permitting a small tunneling along thexdirection.Figure 2(b)plots the phase diagram fortx/t=0.08.In contrast to Fig.2(a),this finite tunnelingtxhas multiple effects on the system.The first is that this tunneling brings some new nodal line super fluid phases(0,0;2,1),(0,0;2,0)and(2,0;2,1).The gapless contours of these new phases are shown in Figs.3(c)–3(g).The calculations of topological invariants signify that these new phases are also topologically protected.From the viewpoint of dimensional reduction,the topological stability of nodal lines indicates that 1D subsystems enter into topological super fluid phases,which requires a large Zeeman field alongzdirection for systems with s-wave interaction and SOC.[42−43]Since thetxterm in the Hamiltonian(1)is akin to a nonuniform Zeeman field in the momentum space along thezdirection,so that this tunneling also enlarges the phase space for nodal line super fluid phases.Finally,as mentioned above,a finite tunnelingtxdisplaces in the opposite direction the gapless contours onkx=0 andkx=πplanes,thusw(ky,kz)andγ(ky,kz)can be nonzero and the zeroenergy surface states(Fig.4)appear for the regions between the split nodal lines.

Fig.4 (Color on line)The zero-energy surface state spectral function in ky-kzsurface BZ for nodal line super fluid phases(0,0;2,0)(a),(2,0;2,0)(b),(2,1;2,1)(c),(2,0;2,1)(d).The red regions have large spectral weight of zero-energy.The parameters are the same as those in Fig.3 for the corresponding phases.The surface state spectral function can be conveniently obtained by the technique of Green function iteration.[44]The regions owning surface states are consistent with the regions with nonzero topological invariants in Fig.3 and the bulk-boundary correspondence is corroborated.

4 Discussions and Conclusions

In the maintextty=tz=tis assumed and all nodal lines are closed in 3D BZ.If we adjust the strengths of lasers used to create optical lattices alongyandzdirections to permit the anisotropyty=tz,some nodal lines will become open(see Fig.3(h)).These open nodal lines stretch continuously from one side to the other of the BZ.Thus when we adjustty/tzand fix all other parameters,it is possible to realize a Lifshitz phase transition,in which the Fermi surface of the ground state changes its topological structure.For these open nodal lines,considering the fact that the two ends of such a nodal line are identified due to the periodicity of the momentum in BZ,the topological invariants(7)and(8)remain to be defined.Our numerical results suggest that these open nodal lines are also topologically stable.

The Hamiltonian(1)in 3D can be easily extended to 2D by settingtz=0 andk=(kx,ky).This is also experimentally feasible by increasing the strength of optical lattice alongzdirection to freeze the corresponding degrees of freedom.In this case the gapless conditions(4)and(5)define some isolated Dirac-type nodal points in 2D BZ.The fermion doubling theorem ensures their appearance in pair.[45]The topological stability of these nodal points can also be characterized by invariants(7)and(8).In 2D these gapless nodal point topological super fluid phases can show zero-energy flat band on the edges of the system,which is widely discussed in the condensed matter physics.[46−51]We have numerically self-consistently checked these conclusions in 2D.

The presence of nodal line(point)super fluid states highly depends on whether the ground state is BCS or FFLO.If the ground state is FFLO,the TRS and chiral symmetry will be spontaneously broken and the topologically stable nodal lines(points)will be destroyed.In order to exclude the possibility of FFLO state along different directions,we have investigated the behavior of thermodynamic potential as the function of paring momentum by self-consistently solving order parameter∆.We find that the thermodynamic potential increases with the increase of pairing momentum.Thus FFLO phase is impossible in terms of parameters we studied.This numerical check further addresses the validity of nodal phases in the suggested system.

To conclude,we have self-consistently studied the phase diagrams of 3D ultracold fermionic gases with 1D SOC and transverse Zeeman field.This system is experimentally feasible and with the increase of transverse Zeeman field can evolve into nodal line topological super fluid,which can be regarded as the super fluid counterpart of nodal line semimetal in the condensed matter physics.In

[1]Y.J.Lin,K.Jiménez-Garc´Ia,and I.B.Spielman,Nature(London)471(2011)83.

[2]J.Y.Zhang,S.C.Ji,Z.Chen,et al.,Phys.Rev.Lett.109(2012)115301.

[3]L.W.Cheuk,A.T.Sommer,Z.Hadzibabic,et al.,Phys.Rev.Lett.109(2012)095302.

[4]P.Wang,Z.Q.Yu,Z.Fu,et al.,Phys.Rev.Lett.109(2012)095301.

[5]Z.Wu,L.Zhang,W.Sun,et al.,Science 354(2016)83.

[6]Z.Zheng,M.Gong,X.Zou,et al.,Phys.Rev.A 87(2013)031602.

[7]Z.Zheng,M.Gong,Y.Zhang,et al.,Scienti fi c Reports 4(2014)6535.

[8]Y.Xu,C.Qu,M.Gong,and C.Zhang,Phys.Rev.A 89(2014)013607.

[9]F.Wu,G.C.Guo,W.Zhang,and W.Yi,Phys.Rev.Lett.110(2013)110401;Phys.Rev.A 88(2013)043614.

[10]Y.Cao,X.J.Liu,L.He,et al.,Phys.Rev.A 91(2015)023609.

[11]C.Qu,Z.Zheng,M.Gong,et al.,Nat.Commun.4(2013)2710.

[12]W.Zhang and W.Yi,Nat.Commun.4(2013)2711.

[13]Y.Cao,S.H.Zou,X.J.Liu,et al.,Phys.Rev.Lett.113(2014)115302.

[14]C.F.Chan and M.Gong,Phys.Rev.B 89(2014)174501.

[15]X.J.Liu,H.Hu,and H.Pu,Chin.Phys.B 24(2015)050502.

[16]H.Hu,L.Dong,Y.Cao,et al.,Phys.Rev.A 90(2014)033624.

[17]H.Hu and X.J.Liu,New J.Phys.15(2013)093037.

[18]X.J.Liu and H.Hu,Phys.Rev.A 87(2013)051608.

[19]X.F.Zhou,G.C.Guo,W.Zhang,and W.Yi,Phys.Rev.A 87(2013)063606.

[20]L.S.Xie,L.M.Schoop,E.M.Seibel,et al.,APL Mat.3(2015)083602.

[21]Y.Chen,Y.M.Lu,and H.Y.Kee,Nat.Commun.6(2015)6593.

[22]G.Bian,T.R.Chang,R.Sankar,et al.,arXiv:condmat/1505.03069.

[23]H.Weng,Y.Liang,Q.Xu,et al.,Phys.Rev.B 92(2015)045108.

[24]Y.Chen,Y.Xie,S.A.Yang,et al.,Nano Lett.15(2015)6974.

[25]D.W.Zhang,Y.X.Zhao,R.B.Liu,et al.,Phys.Rev.A 93(2016)043617.

[26]V.Gurarie,L.Radzihovsky,and A.V.Andreev,Phys.Rev.Lett.94(2005)230403.these novel super fluid phases,there exists the dispersionless zero-energy flat band in a fi nite region of the surface BZ.Experimentally these nodal line super fluid states can be detected through the momentum-resolved radiofrequency spectroscopy.

[27]C.Zhang,S.Tewari,R.M.Lutchyn,and S.Das Sarma,Phys.Rev.Lett.101(2008)160401.

[28]M.Sato,Y.Takahashi,and S.Fujimoto,Phys.Rev.Lett.103(2009)020401.

[29]M.Gong,S.Tewari,and C.Zhang,Phys.Rev.Lett.107(2011)195303.

[30]Y.Xu,R.L.Chu,and C.Zhang,Phys.Rev.Lett.112(2014)136402.

[31]Y.Xu,F.Zhang,and C.Zhang,Phys.Rev.Lett.115(2015)265304.

[32]B.Liu,X.Li,L.Yin,and W.V.Liu,Phys.Rev.Lett.114(2015)045302.

[33]H.Hu,L.Dong,Y.Cao,et al.,Phys.Rev.A 90(2014)033624.

[34]Z.Fu,L.Huang,Z.Meng,P.Wang,et al.,Phys.Rev.A 87(2013)053619.

[35]J.Zhang,H.Hu,X.J.Liu,and H.Pu,Annu.Rev.Cold At.Mol.2(2014)81.

[36]S.G.Peng,X.J.Liu,H.Hu,and K.Jiang,Phys.Rev.A 86(2012)063610.

[37]Y.X.Zhao and Z.D.Wang,Phys.Rev.Lett.110(2013)240404.

[38]C.K.Chiu and A.P.Schnyder,Phys.Rev.B 90(2014)205136.

[39]B.Béri,Phys.Rev.B 81(2010)134515.

[40]M.Sato,Y.Tanaka,K.Yada,and T.Yokoyama,Phys.Rev.B 83(2011)224511.

[41]R.Yu,H.Weng,Z.Fang,et al.,Phys.Rev.Lett.115(2015)036807.

[42]Y.Oreg,G.Refae,and F.V.Oppen,Phys.Rev.Lett.105 177002(2010).

[43]R.M.Lutchyn,J.D.Sau,and S.Das Sarma,Phys.Rev.Lett.105(2010)077001.

[44]M.P.L.Sancho,J.M.L.Sancho,and J.Rubio,J.Phys.F:Met.Phys.15(1985)851.

[45]H.B.Nielsen and M.Ninomiya,Nucl.Phys.B 185(1981)20.

[46]W.Y.He,B.T.Zhou,J.J.He,et al.,arXiv:condmat/1604.02867.

[47]S.Deng,G.Ortiz,A.Poudel,and L.Viola,Phys.Rev.B 89(2014)140507.

[48]N.F.Q.Yuan,C.L.M.Wong,and K.T.Law,Physica E 55(2013)30.

[49]C.L.M.Wong,J.Liu,K.T.Law,and P.A.Lee,Phys.Rev.B 88(2013)060504(R).

[50]J.You,C.H.Oh,and V.Vedral,Phys.Rev.B 87(2013)054501.

[51]Y.Tanaka,Y.Mizuno,T.Yokoyama,et al.,Phys.Rev.Lett.105(2010)097002.