Generation of different Classes of Multipartite Entanglement Using Cavity-QED

Mustapha Ziane, Rachid El Guerbouz, Fatima-Zahra Siyouri, and Morad El Baz

Equipe Sciences de la Mati`ere et du Rayonnement,Département de Physique Facultédes sciences,Université Mohammed V Av.Ibn Battouta,B.P.1014,Agdal,Rabat,Morocco

1 Introduction

Quantum entanglement plays a very important role in quantum information processing(QIP).[1−7]During the past decade,many suggestions have been presented for entanglement generation.[8−10]Despite the fact that most of the quantum information protocols focus on two-qubit systems,multipartite entanglement has also attracted great interest for its potential applications in QIP and quantum communications.[11−13]There are two typical multipartite entangled states,Greenberger-Horne-Zeilinger(GHZ)and W states,which are usually referred to as maximal entanglement and cannot be converted into each other by local operations and classical communications.In particular,the W-state of three qubits have some interesting properties,for example,it retains a maximal amount of bipartite entanglement when any one of the three qubits is traced out.It is worth noting that apart from these two inequivalent classes of genuine tripartite entanglement there exist four other classes of states;A-B-C class states(these are actually separable states),A-BC class states,AB-C class states and C-AB class states.

On the other hand,QIP using systems of cavity quantum electrodynamics(QED)is one of the dominant distribution information tools.Furthermore,such systems are a qualified alternative candidate for the generation of entanglement. In view of this,several schemes for generating the entanglement via cavity-QED have been proposed.[14−18]In particular,the generation schemes for GHZ[19−21]and W[22−24]states have attracted much more attention.For instance,Zheng have proposed a scheme for the generation of three-particle GHZ states for three atoms trapped in distant cavities.[20]For the same purpose,Wang et al.have proposed a simple scheme for generating a three-atom GHZ state from two EPR states.[21]Similarly,Guo and Zhang have proposed a scheme to prepare three-atom and three-cavity entangled W states.[23]Moreover,Marret al.have investigated W states by adiabatic passages and decoherence free subspace.[24]

In this paper,we propose two schemes to generate entanglement for a system of three qubits via cavity-QED.In this respect,in the first scheme we make a three-level atom interact with three cavities successively exploiting an Hamiltonian of the atom-cavity interaction.[25]As a matter of fact,after the interaction we obtain four classes of tripartite field entanglement;W class states,A-B-C,AB-C and C-AB class states.Then in order to complete the generation of all possible six classes,we present another scheme,in which two three-level atoms successively interact with a coherent optical field exploiting an effective Hamiltonian[26]of interaction between each atom with the coherent field.This allows us to generate the remaining two classes that were not generated using the first proposal.Indeed,our schemes do not generate W-class states and GHZ-class states only but also can generate all the possible classes.Furthermore,in contrast to the previous proposed protocols,several atoms are required to interact with single mode field simultaneously.The current work stands out with the fact that the interaction between atoms and cavities is not simultaneous,which avoids the problem of the synchronization of several atoms in the previous quantum information processing proposals.This advantage helps us to realize our protocols easily and gives more efficiency to our model compared with the references schemes using QED.

The article is divided as follows.In Sec.2,we define quantum entanglement for a system of three qubits by using genuine tangle and recall the characteristics of the different classes of tripartite entanglement.In Sec.3,we propose two schemes:in the first one,we send a three-level atom through three cavitiesC1,C2,andC3successively.In the second one two three-level atoms of Λ-type are successively interacting with a coherent optical field.

2 Genuine Tripartite Entanglement

In a three-qubit system ABC,the qubits may be pairwise entangled,but can also be three-way entangled states that are not pairwise entangled.[27−28]These different types of entanglement can be quantified using several entanglement measures in both theoretical and experimental investigations of quantum information processing.[27,29−30]Here,we will use the genuine tangleτg,as a measure of genuine tripartite entanglement.[28]It is worth noting that what we call here genuine tripartite entanglement is the pure entanglement between the three parties that cannot be described by bipartite entanglement.For instance,when one of the subsystems(say A)is entangled with the other two subsystems combined(BC in this case),the correlation can be understood as a bipartite entanglement between two parties A|BC and is measured as such by any of the well known measures of bipartite entanglement.In that case,the genuine entanglement shall be obtained by subtracting from the A|BC entanglement any bipartite entanglement between party A and each the components of the other subsystems(that is B and C).

Adopting the above definition of genuine tripartite entanglement,the genuine tangleτgof three qubit systems is expressed as,

whereλ1,λ2,λ3,andλ4are the non-negative eigenvalues of the matrixarranged in decreasing order with the“Spin Flipped” density matrix being defined by

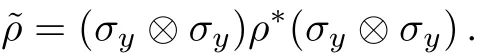
3 Multipartite Entanglement Generation

3.1 Cavity Field Entanglement and W-Class States

In order to generate W-class states in terms of the cavity fields,we propose a scheme in which we send a threelevel atom through a system of three cavitiesC1,C2,andC3successively(see Fig.1),whereC1,C2,andC3are prepared initially in their vacuum states.We may express the eigen-energies of the three levels,asEe,EiandEg.In this proposal,the dipole transitions are allowed between the three levels of the atom.We consider that frequenciesω1,ω2,andω3of the three-mode cavity field are in resonance with two transition frequencies,such that

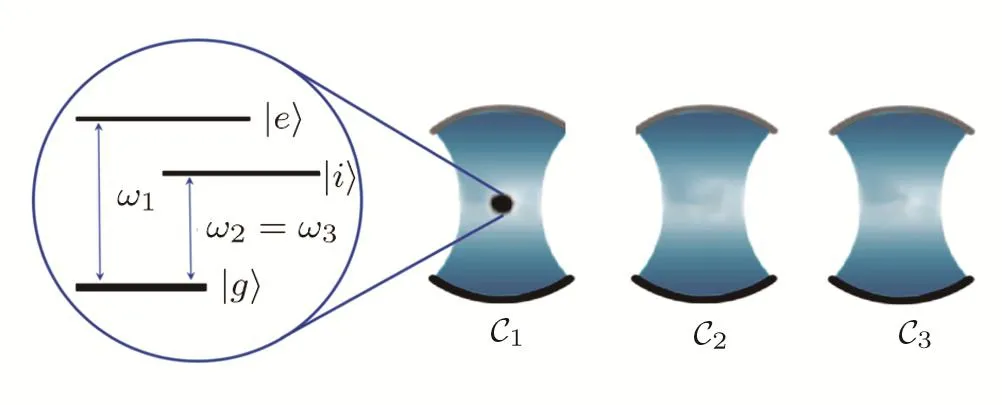
Fig.1 Interaction between one a three-level atoms with three cavities.

Initially,the active atom is in the superposition state>(the probability amplitudesαandβsatisfy the normalization conditionthe cavity fieldsC1are in a vacuum state.So we may express the initial state of the system atom-cavityC1as,

whereH1is already defined in Eq.(5).

Solving the coupled differential equations obtained from the Schrödinger equation yield the solutions:C1e0=Hence,after interacting with the first cavity the atom field state is written as,

The atom is now brought to interact with the second cavityC2.The Hamiltonian describing this interaction is similar to Eq.(5)with the appropriate change of indices:

The state so obtained Eq.(13)is reminiscent of theWstates.In Sec.4 we will detail how to obtain the exactWsates,as well as three other classes of tripartite states out of this state simply by fixing the interaction times.

3.2 Atomic-Field Entangled States and GHZClass States

In order to complete the generation of all possible six classes,we present another scheme that will allow us to generate the remaining two classes which were not generated using the previous proposed scheme.The purposed scheme makes use of the coherent cavity field.

Coherent states have been found to play an essential role in quantum information processing,for ensuring or teleporting an unknown quantum state.Moreover,they are a specific type of quantum states applicable to the electromagnetic field that describe a maximal type of coherence.On the other hand,the generation of the coherent state can be done by simple lasers,in view of this,the use of optical fields in any protocol makes its realization possible.The Fock state expansion of the single-mode coherent state,[31]is given by

where|n>is the Fock state of the corresponding photon number andαis the amplitude of the coherent state.For our propose,we consider two three-level atoms of Λ-type successively interacting with a coherent optical field(see Fig.2).In this proposal,the two lower levels of the atoms are degenerate,and the cavity field frequencyωc(coherent field frequency)is extensively detuned from the frequency of the atomic transitionω0between the lower levels and the upper level.In this case,large detuning limitδ≫g,the upper level of the atoms may be adiabatically excluded during the interaction.

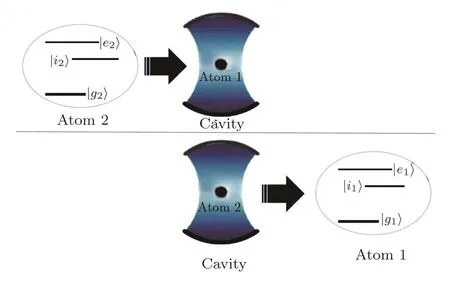
Fig.2 Two three-level atoms interact successively with a coherent optical field.

The effective Hamiltonian of the system(atom- field)is expressed as follow[26,31]

withg1,g2being the coupling constants between the cavity mode transitions>respectively,a†(a)is the creation(annihilation)operator for the cavity mode andδ=ω0−ωcbeing the detuning between the transition frequency of the atom and the frequency of the coherent field.

In the following,we suppose thatg1=g2=gandThus,Eq.(16)can be rewritten as

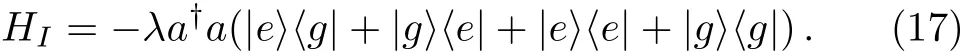
If we consider that the atom is initially prepared in the state|e>,and the optical field is in the coherent state|α>:

Now,after the first atom>has interacted with the coherent optical field forwe pass the second atom,initially prepared in>state,through the same optical field.We consider that the interaction time is stillthen the state for the whole system is given by,

The state obtained is entangling the cavity field and the atoms used in a GHZ manner of tripartite entanglement.

4 Main Results

We start by studying the behavior of the state(13)obtained using the first protocol and the different classes of entanglement that it can generate.For this purpose,we plotted in Fig.3 the variation of the different types of tripartite entanglement with respect to the three interaction timest1,t2,andt3.In each one of the plots we fix the interaction times of two cavities adequately and study the behavior with respect the third time.

Figures 3(a)and 3(b)show that the first scheme can generate four state-classes by adequately adjusting the interaction times.For instance,Fig.3(a)shows that by fixing the interaction time in the second and third cavity,one generates A|BC entanglement.Moreover,in this case for the interaction time with the first cavityt1=nπ/g1,the entanglement between the modes B and C can reach its maximal value in the form of the state

The price for this,obviously due entanglement monogamy,is that the first field is going to be disentangled for the remaining two fields.

Similarly,Fig.3(b)shows that fixing the interaction time in the first and second cavity adequately allows to generate the class AB|C.For some specific values of the interaction time with the third cavitythe entanglement between the modes A and B reaches its maximal value and the state of the AB subsystem is

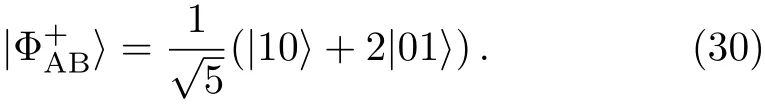
It is remarkable that the completely separable states can be obtained from Eq.(13)by canceling two of the three terms in Eq.(13).For example fixing the interaction timesAside from the aforementioned interaction timesthe states thus generated are in the W-class state.Of course,particular choicesandwithnan even integer,allow generating maximally entangled W-states between the three modes.

In order to understand more deeply the behavior of these four classes of quantum correlations,we plotted in Fig.4 their variation as a function oft1for fixed values oft2andt3(Fig.4(a))and as function oft1andt3for a fixedt2(Fig.4(b)).

Figures 4(a)and 4(b)allow for deep study of the behavior of these classes of quantum correlations.For this purpose Fig.4(b)shows the behavior,as a function oft1andt3for a fixedt2,of the bipartite correlations between A and B,B,and C and between B on one hand and the subsystem AC as a single subsystem on the other hand.Interestingly enough,both figures show a perfect transfer of entanglement between the different modes,thus preserving the entanglement monogamy.For instance,one can see that a maximized entanglement between modes B and C precludes any correlation with mode A;as the correlations between any two modes loosen up,their correlations with the other mode tighten up.

Fig.3 Entanglement behavior of the generated state(13)with respect to:(a)g1t1for fixed values of g2t2and g3t3;(b)g3t3for fixed values of g1t1and g2t2.

So far the first scheme presented allowed us to generate four classes of tripartite entanglement.The remaining two classes can be generated using the second scheme presented as we are going to show in the following study of the behavior of state(28).We plotted in Fig.5 the variation of genuine entanglementτg,bipartite entanglementEi|jkandEi|jas a function of the coherent amplitudeα.

The figure shows that the bipartite entanglementEi|jis absent for all values ofα,which means that,the bipartite systems(AB,BC,and AC)are not entangled.Such a behavior is a characteristic of GHZ entanglement.Furthermore,it is seen that both the entanglementEi|jkand genuine entanglementτgincrease with increasing values of the coherent parameterα.For large values of coherent amplitudeα≥1 the entanglementEi|jbecomes equal to genuine entanglement,and both attain their maximum value.Therefore,one can assert that after interaction between the two atoms and the cavity as described in the scheme one can generate GHZ-class states and B-AC class states.It is worth noting that such a scheme creates a correlation between the atomic degrees of freedom(mode B),field degrees of freedom(mode A)and the atomic degrees of freedom(mode C)in a GHZ manner.

Fig.4 Entanglement behavior of the generated state(13)as a function of:(a)t1for fixed values of t2and t3;(b)t1and t3for a fixed t2.

Fig.5 Variation of the entanglement of the generated state(28)with respect to the coherent amplitude α.

We deem that our schemes are realizable using nowadays technologies.For instance we propagate a beam of Rubidium atoms in higher Rydberg states which have life time of the order of few milliseconds trough an optical quantum field of wavelength in microwave region in high-Q superconducting cavity of dimension of a few centimeters with the frequenciesω1=105.4 GHz andω2=ω3=54.3 GHz.The effective interaction timetis set to 19µs by selecting atoms with a velocity of 400 m/s,which is far less than the cavity life times.[32]

5 Conclusion

In summary,we have proposed two schemes to prepare tripartite entangled states.The combined two schemes allow to generate all possible classes of tripartite entanglement,especially the flagships W-states and GHZ-states.Moreover,the schemes presented allows to generate entanglement between the cavity fields degrees of freedom(from the first scheme),and a mixed entanglement between the cavity field degrees of freedom and the atomic degrees of freedom.

The proposed schemes are easy enough in their conceptions and can be generalized actually to generate multipartite entanglement beyond the tripartite one discussed in this paper.For instance,the first scheme can be generalized by usingncavity fields that are going to be correlated in a generalizedn-partite W-state manner.Similarly,the second scheme can be generalized by usingn–1 atoms,interacting with a single cavity.The result will be a generalizedn-partite GHZ-type of entanglement between then−1 atoms and the cavity field.

On the other hand,the proposed schemes are easy in their conception in the sense that they can be realized using nowadays technology.This will make it a good candidate to implement different quantum information processing tasks.

[1]Y.B.Sheng and L.Zhou,Sci.Rep.5(2016)13453;Y.B.Sheng and L.Zhou,Sci.Bull.62(2017)1025.

[2]F.Z.Siyouri,Commun.Theor.Phys.68(2017)729.

[3]Y.B.Sheng,J.Pan,R.Guo,et al.,Sci.China-Phys.Mech.Astron.58(2015)060301.

[4]Q.H.Liao,Q.Zhang,J.Xu,et al.,Commun.Theor.Phys.65(2016)684.

[5]Z.Li,Commun.Theor.Phys.68(2017)57.

[6]W.Zhang,D.S.Ding,Y.B.Sheng,et al.,Phys.Rev.Lett.118(2017)220501.

[7]F.Zhu,W.Zhang,Y.Sheng,and Y.Huang,Sci.Bull.62(2017)1519.

[8]B.H.Huang,Y.H.Chen,Q.C.Wu,et al.,Laser Phys.Lett.13(2016)105202.

[9]X.X.Yi,G.R.Jin,and D.L.Zhou,Phys.Rev.A 63(2001)062307.

[10]S.G.Zheng,Phys.Rev.A 63(2001)015801.

[11]C.H.Bennett,D.P.DiVincenzo,J.A.Smolin,and W.K.Wootters,Phys.Rev.A 54(1996)3824.

[12]S.B.Zheng,Phys.Rev.A 65(2002)051804(R).

[13]Y.Liang,S.L.Su,Q.C.Wu,et al.,Opt.Exp.23(2015)5064.

[14]S.B.Zheng and G.C.Guo,Phys.Rev.Lett.85(2000)2392.

[15]S.Osnaghi,P.Bertet,A.Au ff eves,et al.,Phys.Rev.Lett.87(2001)037902.

[16]C.J.Huang,M.Zhou,J.F.Li,and H.Y.He,Acta Phys.Sin.51(2002)805.

[17]G.Y.Wang,Q.Ai,B.C.Ren,et al.,Opt.Exp.24(2016)28444.

[18]Y.H.Chen,Y.Xia,Q.Q.Chen,and J.Song.Phys.Rev.A 91(2015)012325.

[19]S.B.Zheng,Phys.Lett.A 372(2008)591;S.B.Zheng,Phys.Rev.Lett.87(2001)230404.

[20]S.B.Zheng,Euro.Phys.J.D 54(2009)719.

[21]W.Jun,L.B.Yu,and Y.Liu,Chin.Phys.16(2007)2211.

[22]J.I.Cirac and P.Zoller,Phys.Rev.A 50(1994)R2799.

[23]G.C.Guo and Y.S.Zhang,Phys.Rev.A 65(2002)054302.

[24]C.Marr,A.Beige,and G.Rempe,Phys.Rev.A 68(2003)033817.

[25]S.B.Zheng,Phys.Rev.A 71(2005)062335.

[26]L.Xu and Z.M.Zhang,Z.Phys.B 95(1994)507.

[27]V.Co ff man,J.Kundu,and W.K.Wootters,Phys.Rev.A 61(2000)052306.

[28]R.Horodecki,P.Horodecki,M.Horodecki,and K.Horodecki,Rev.Mod.Phys.81(2009)865.

[29]G.Romero,C.E.López,F.Lastra,et al.,Phys.Rev.A 75(2007)032303.

[30]L.Zhou and Y.B.Sheng,Phys.Rev.A 90(2014)024301.

[31]C.Gerry and P.Knight,Introductory Quantum Optics,Cambridge University Press,New York(2005).

[32]A.Rauschenbeutel,G.Nogues,S.Osnaghi,et al.,Science 288(2000)2024.