Semi-Relativistic Two-Body States of Spinless Particles with a Scalar-Type Interaction Potential

K.E.Thylwe

KTH-Mechanics,Royal institute of Technology,S-100 44 Stockholm,Sweden

1 Introduction

Relativistic two-body effects may be studied using quantum field equations,[1]two-body Dirac equations,[2−6]and/or by equations resulting from direct quantum operator substitutions ofandThe latter approach explored in this study ignores spins other than orbital angular momenta.Many relevant references can be found in those cited.

Semayet al.[2]and Ferreira[3]showed explicit results from a 16-components Dirac approach for scalar potentials of the con fi ning type and bound states with vanishing total spin.The main interest of these authors is related to quark spectra.The relevant second-order differential equations obtained are simple and provide some understanding of important two-body effects.

Duviryak(2008),[4]also applying a Dirac-type method,presented solvable two-body models in connection with light mesons and Regge trajectories.No explicit results for scalar potentials are given.However,the general results seem to be relevant in the present context.

Moshinsky and Requer(2003)[6]studied two equal fermionic masses in the context of positronium formations.It seems close to other procedures related to sub-atomic interactions.No explicit results for scalar potentials are given.

In the present study the semi-relativistic approach[8−10]is applied with scalar(mass-type)potentials.In addition a“local-momentum”approximation is suggested to find the Dirac-type equations of Refs.[2–4]for two-body spectra with vanishing total spin.

The basic equations for calculating bound state energies are presented in Sec.2.Section 3 is devoted to a linear quark-type potential model.Two-body effects on selected bound state energies near the non-relativistic limit are illustrated.Conclusions are in Sec.4.

2 Semi-relativistic Local-Momentum Equations

In this section the“local-momentum”approximation used to simplify the semi-relativistic equation is outlined.This approach appears to be closely related to the one of Krolikowski.[7]The semi-relativistic quantum(SRQ)approximation of two interacting spinless particles starts from a Hamiltonian of classical special relativity.For an instantaneous scalar potentialS(r)in the center-of-mass frame of two massive particles,the stationary SRQ quantal wave functionψsatisfies the equation

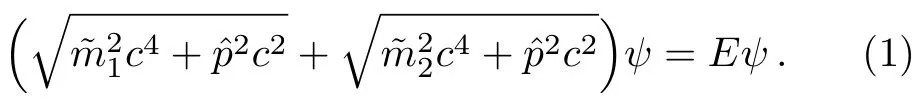
Here,Ethe relativistic energy,cis the speed of light andthe two momentum operators.The mutual scalar potentialS(r)and masses are combined:

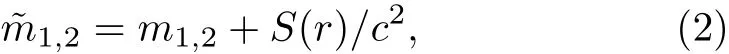
withm1,2being the rest masses.

The momentum operatoris the same for both particles in a centre-of-mass frame(although moving in opposite directions).The momentum operator is given by the cartesian and the radial expressions as

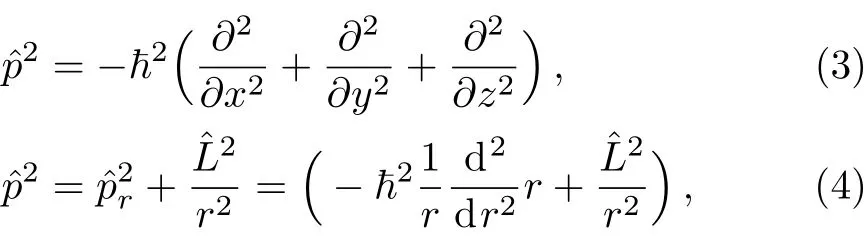
whereis the orbital angular momentum operator and~the reduced Planck’s constant.

The equations of the local-momentum approximation can be derived by imagining two particles entering from free space towards a finite interaction region.In free space a plane wave eikz,with a given wave numberk,is repre-sented by the partial wave series[11]

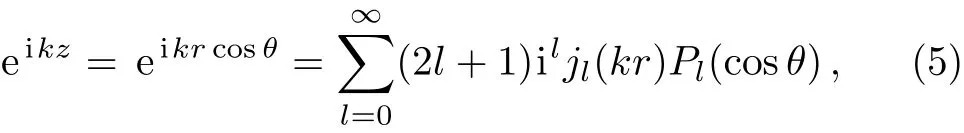
wherel=0,1,...are the orbital angular momentum quantum numbers.The Legendre polynomialsPl(cosθ)are expressed in terms of the angleθbetween the initialz-direction and the relative position vector.

By expanding the square roots in the basic SRQ equation(1),and using the cartesian representation(3)ofˆp2,this equation(1)provides the exact asymptotic wave numberkfor freely propagating plane waves e±ikz:

A formal expansion of the operator in terms ofˆp2in thel-term of Eq.(1),i.e.in

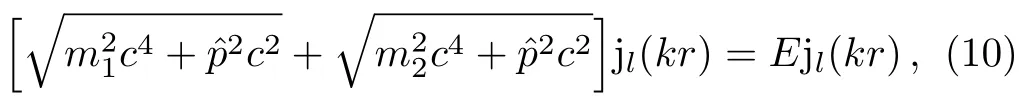
leads after some algebra to Eq.(6).

Hence,the plane wave satisfies Eq.(1)and its partial wave component satisfies(9)as well as(10).

A generalization of the above semi-relativistic observations for plane waves leads to thelocal-momentum approximation.To this end,let a general wave be expanded as

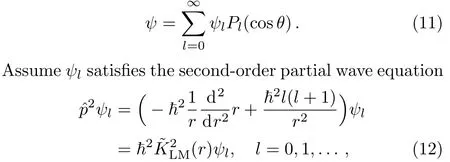
wherein Eq.(12)is anunspecifiedscalar function ofr.Ifis not constant,higher powers ofare now assumed to satisfy the “approximate” relations

being accurate for sufficiently slowly varying functionsIt follows that the wave functionψlin Eq.(12)solves Eq.(1)approximately.The left hand member in Eq.(1)is approximated,yielding

2.1 Non-relativistic limit

By letting the relevant non-relativistic energyϵbe defined by

For equal massesm=4µand for extreme light-heavy mass systemsµ/m→0,which can be considered also the single-mass limit in an external scalar potential 2S.

In the single-mass limit the coefficient in Eq.(20)simplifies to

Table 1 Local-momentum energy levels for the linear potential in Eq.(28)with selected values of α2/4 and µ/m.

This agrees with anexact spin symmetrymodel of the light-heavy quark-mass system in Ref.[12],provided the light mass component is represented byµ.Also,2S(r)in Eq.(21)represents the sum of the equal“external” scalar and(time-component)vector potentials in Ref.[12].As realized from Eq.(20),two-body effects(relative to nonrelativistic results)relate to the total massmbeing finite rather than in finite.

3 Linear Scalar Potential

Equation(18)is transformed into non-dimensional form for a linear scalar potential defined by

wherer∗andα2µc2are independent of the speed of light.The potentialS(r)is likewise reduced to

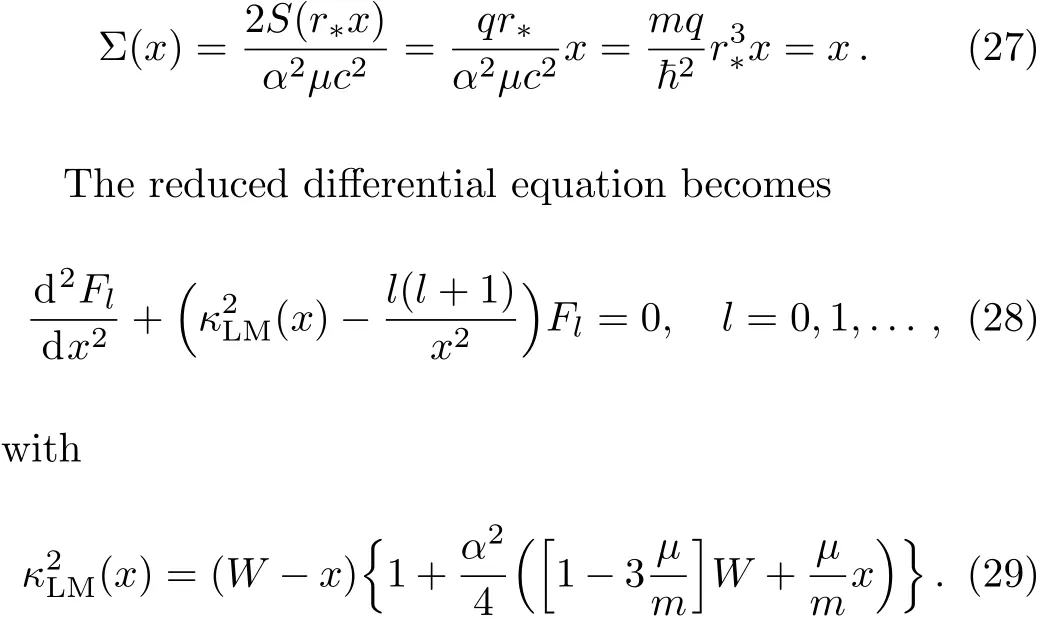
In Eq.(29)µ/mrepresents the two-body parameter being magnified by the relativistic parameterα2as this becomes large.The two extreme cases areµ/m=0 andµ/m=1/4.A semi classical analysis of the coefficientindicates that turning points are not affected by the relativistic terms.Also(x,α=0)in the oscillating region of the effective potential,implying that energy levels are expected to appear shifted to lower values asαincreases.

Fig.1 (Color on line)Energy levels(W)as function of relativity(α2/4)and the two-body parameterµ/m.The quantum numbers are l(orbital angular momentum)and n(radial nodes).From top:Purple lines:l=2,n=0.Solid line corresponds to equal masses,dashed line to the single mass limit.Green lines:l=0,n=1.Solid line corresponds to equal masses,dashed line to the single mass limit.Red,black respectively blue lines:l=1,n=0:µ/m=0.25(equal masses),=0.125(in between),respectively=0(single mass).Red,black respectively blue lines:l=0,n=0:µ/m=0.25(equal masses),=0.125(in between),respectively=0(single mass).

Numerical computations based on Eq.(28)are performed using an amplitude-phase method.[13]Figure 1 shows how energy levels are shifted as function ofα2/4 with different values of the two-body parameterµ/m.The reduced massµis considered fixed and the quantum numbers arel(orbital angular momentum)andn(radial nodes).Levels corresponding to the single-mass limit are the ones most sensitive to relativistic corrections.A possible explanation is that in this limit one of the masses is as small as possible for a given reduced massµ.Note that all levels investigated are shifted to lower values asαincreases.

The level spacing with respect tonis wider than that with respect tol(see Fig.1),and only the lowest energy levels are considered in Fig.1.

4 Summary

An approximation of the semi-relativistic approach,the“local-momentum approximation”, is outlined.Bound-state conditions appear similar to those of two body approaches based on the Dirac theory for fermions.

The two-body effect found is that single-mass conditions are more sensitive to relativistic corrections.In the single-mass limit a spectrum corresponding to the spin symmetry of the single-particle Dirac equation is obtained.

[1]E.E.Salpeter and H.A.Bethe,Phys.Rev.84(1951)1232.

[2]C.Semay,R.Ceuleneer,and B.Silvestre-Brac,J.Math.Phys.34(1993)2215;C.Semay and R.Ceuleneer,Phys.Rev.D 48(1993)4361.

[3]P.L.Ferreira,Phys.Rev.D 38(1988)2648.

[4]A.Duviryak,SIGMA 4(2008)048.

[5]W.Krolikowski and J.Rzewuski,Acta Phys.Pol.B 7(1976)487;H.Joos,J.Leal Ferreira,and A.H.Zimerman,Nuovo Cimento 5(1957)57;J.Leal Ferreira and A.H.Zimerman,An.Acad.Bras.Cienc.30(1958)281;H.M.Moseley and N.Rosen,Phys.Rev.80(1950)177;M.Nagasaki,Frog.Theor.Phys.37(1967)437;A.O.Barutand and G.L.Strobel,Few-Body Systems 1(1986)167;I.J.Nickisch,B.Durand,and L.Durand,Phys.Rev.D 25(1982)2312.

[6]M.Moshinsky and V.Riquer,J.Phys.A 36(2003)2163.

[7]W.Krolikowski,Acta Phys.Pol.B 12(1981)793;W.Krolikowski,Acta Phys.Pol.B 11(1980)387.

[8]S.M.Ikhdair and R.Sever,IC/92/186,INTERNAL REPORT(1992);Int.J.Mod.Phys.E 17(2008)1107;Int.J.Mod.Phys.A 20(2005)16509.

[9]S.Hassanabadia,M.Ghominejada,and K.E.Thylwe,Commun.Theor.Phys.63(2015)423.

[10]K.E.Thylwe,O.J.Oluwadare,and K.J.Oyewumi,Commun.Theor.Phys.66(2016)389.

[11]N.F.Mott and H.S.W.Massey,The Theory of Atomic Collisions,Clarendon Press,Oxford(1965)Ch.2.

[12]K.E.Thylwe and M.Hamzavi,J.Phys.A 46(2013)085305.

[13]K.E.Thylwe,J.Math.Chem.53(2015)1608.