基于星间链路技术的地球静止轨道卫星定轨精度分析
2018-05-23,,,,
, , , ,
(西北核技术研究所,西安 710024)
0 引言
轨道高度为3.6万公里的GEO 卫星具有相对地球静止的特性。GEO 卫星应用日益增多,今天大约 300 颗有效卫星在此轨道上,在北美洲、欧洲和亚太时区静止轨道卫星分布密度较大,GEO卫星在高分辨率对地观测、气象、远程通信活动等领域都发挥着越来越重要的作用[1],对其轨道确定的需求也越来越高,研究对GEO卫星的实时自主定轨方法已经迫在眉睫。
传统的地面定轨手段已难以满足 GEO 卫星高精度应用的需求。图1简要说明了不同观测点对GEO卫星的观测情况,中间实心大圆表示地球,地球上加粗弧段表示我国地面站可布站的范围,6个实心小圆表示MEO卫星,空心小圆表示GEO卫星。卫星对整个地球的张角仅17.6°。我国的经度范围为东经73°至东经135°,GEO对国内地面站的张角仅8.6°。通过国内布设地面站获取的星地观测数据对GEO进行定轨[2]存在两个问题:第一,目前采用的星地测距系统中系统差比较显著,设备时延导致的星地测量系统误差难以通过自校准的方式进行控制,需借助高精度地面测量系统(如激光测距系统)对此进行标定,增加了GEO卫星定轨对地面的依赖性;第二,由地面站与GEO卫星组成的定轨的观测几何很差,导致星地测量的测量误差在定轨的过程中被放大倍数较大。
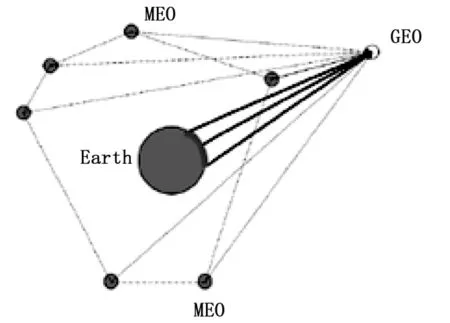
图1 不同情况下对GEO卫星的观测示意图
利用GPS卫星实现对GEO卫星的定轨存在可见卫星数量少,接收到的信号微弱,测量精度不够的问题。故需要寻找其他方法提高GEO卫星的定轨精度。
我国的全球卫星导航系统设计并具备利用星间链路进行测距的功能[3]。星间链路[4]是卫星之间进行星间通信和星间测量的链路,若某两颗卫星之间建立了星间链路,则它们相互之间能够进行彼此相对距离、速度、时差的测量;能够进行快速、高安全性的数据交换,减轻地面运控压力、降低对地面的测控需求、提高卫星星座系统的抗摧毁能力;由于政治、国土范围等因素的影响,我国境内地面站的布局受限严重,星间链路技术可以打破传统布站方式中的局限性。正是由于导航星座星间链路为导航系统所带来的巨大潜力,星间链路已经成为未来全球卫星导航系统的基本技术特征和技术制高点。在基准MEO卫星与待定轨的GEO卫星之间建立的星间链路,具有对GEO卫星观测几何好等优点,为GEO卫星的实时自主定轨开辟一条新的思路。
星间链路资源作为一种新型的战略资源,在太空中承担着纷繁复杂的任务,实际上可以提供给GEO卫星进行定轨的链路资源是有限的。在可用的链路资源数量和观测频度一定的情况下,需要选择与GEO卫星观测几何较好的MEO卫星组合对GEO进行定轨观测来保证GEO卫星的定轨精度,如何选择合适的MEO卫星组合具有重大的实际意义。在考虑星间可见性时,暂时不考虑星间链路频段所对应的天线方向,认为MEO卫星和GEO卫星只要不受地球遮挡即可见。从评价星间链路构型的指标出发,确定了三种选星策略,并分析了不同观测频度以及不同链路数量下GEO卫星的定轨精度。
1 方法与推导
1.1 PDOP值的定义与计算
测量误差将导致基准MEO卫星与GEO卫星之间的距离出现误差,进而导致计算出来的GEO卫星轨道出现误差[5]。在卫星定轨中,我们使用位置精度衰减因子来衡量观测卫星的空间几何分布对定位精度的影响。位置精度衰减因子(position dilution of precision,PDOP,下文简称精度因子)指的是伪距测量误差到卫星定轨三维位置误差的放大倍数[6]。一般来说,PDOP值越大,定轨误差越大,定轨精度越低。为得到PDOP值的计算公式,从伪距测量量对三维位置的偏导数矩阵G出发,有:
(1)
公式(1)中,x、y、z表示的是GEO卫星的坐标值,x(i)、y(i)、z(i)、ρ(i)分别表示的是第i颗与GEO卫星可见的MEO卫星的坐标值和这颗MEO卫星与GEO卫星的星间伪距测量值。
最小二乘准则下,有关测量误差对卫星估计轨道误差影响的详细推导见参考文献[7]。本章直接给出由公式(1)得到的权系数矩阵H:
(2)
PDOP值的计算公式为:
(3)
1.2 链路数量与PDOP值的关系

Hm=GmTGm=Gm-1iTGm-1i+giTgi=Hm-1i+giTgi
(4)
公式(4)中,gi为第i颗MEO卫星对GEO卫星的观测矢量。
由Shermarr Morrison公式可得:
Hm-1i= (Gm-1iTGm-1i)-1= (GmTGm-giTgi)-1=
Hm+HmgiT(1-giHmgiT)giHm
(5)
(6)
(7)
(8)
由公式(8)可知,PDOP值随着与GEO卫星建链的MEO卫星数量的减少而单调增加。当PDOP>6时,定轨方程趋于病态,定轨误差变化幅度增大,定轨精度难以确定[8],故应选择PDOP<6时的链路构型进行建链。
1.3 三种选星策略
由上述推导可知,选择建链的MEO卫星越多,PDOP值越小,去掉第i颗MEO卫星后的PDOP值为pdopi,且pdopi>pdop,pdopi越大,代表去掉第i颗MEO卫星后PDOP值增加越大,说明存在此颗MEO卫星的情况下几何观测构型越好。用pdopi代表第i颗MEO卫星的优先级,下面给出三种基于MEO卫星的优先级的选星策略。
1.3.1 遍历选星策略
遍历选星策略是计算所有不同r颗MEO组合时相应的PDOP值,从而找出PDOP值最小时对应的链路构型作为最优链路构型。
1.3.2 直接选星策略
假定总的链路条数为m,选择用于进行GEO卫星定轨的链路条数为r:
第一步:根据PDOP值的计算公式计算整体的pdop和r颗卫星相应的pdopi;第二步:将m颗卫星相应的优先级按从大到小排序;第三步:选择优先级较高的前r颗MEO与GEO进行建链;
直接选星策略是直接选出对PDOP值贡献较大的前r颗MEO。这种资源配置策略获得的链路构型未必是最优的,因为这种策略仅仅计算了m颗可见星在第一次参与计算时的优先级。其流程图如图2所示。
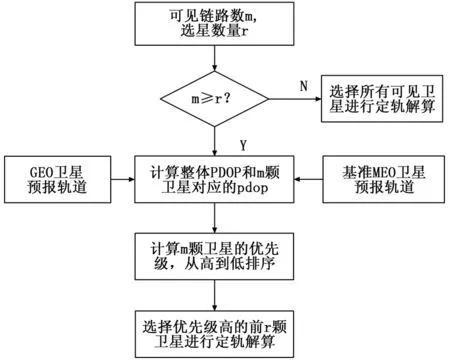
图2 直接选星策略流程图
1.3.3 迭代选星策略
针对直接选星策略存在的问题,提出了迭代选星策略。假定总的链路条数为m,选择用于进行GEO卫星定轨的链路条数为r:第一步:根据PDOP值的计算公式计算整体的pdop和m颗卫星相应的pdopi;第二步:将m颗卫星相应的优先级按从大到小排序。剔除优先级最低的一颗卫星,此时剩下m-1颗卫星,不妨令left为剩余卫星数;第三步:判断剩余的卫星数量left,若剩余的卫星数量大于r,则将left赋值给m,并循环第一步、第二步;若剩余的卫星数量等于r,此时停止选星;
由上面的分析可知,迭代选星策略是循环进行剔除优先级最低的卫星,重新计算卫星优先级两个步骤。其流程图如图3所示。

图3 迭代选星策略流程图
2 实验仿真
2.1 仿真条件
实现GEO卫星的定轨,需要提供GEO卫星的初始轨道信息、MEO卫星的轨道信息,GEO-MEO星间观测数据等,这些数据均由BDSim软件提供。BDSim是我国首个全球卫星导航系统仿真软件工具,由卫星导航仿真与测试实验室(简称“北斗开放实验室”)发布。本文利用BDSim仿真生成观测数据,同时导出观测数据仿真时的卫星轨道,将该轨道视为参考轨道用于后续的定轨精度评估中。采用的定轨评估指标是在GEO卫星R/T/N三个方向的定轨误差绝对值的最大值、RMS值以及定轨三维位置误差的RMS值。RTN坐标系是以卫星自身质心为原点,以从地心指向卫星质心的方向为R方向,卫星运动方向为T方向,N方向与R方向和T方向成右手系。
本文仿真时间为2015年10月1号12:00至2015年10月8号12:00,定轨时间间隔为5分钟。基准星座选择轨道高度为21 528 km,轨道倾角为55°的北斗MEO星座。在J2000.0地心惯性坐标系下,MEO星座种子卫星的初始位置矢量为(单位:m)(16 983 361.424 781,-20 353 706.441 348,-0.001 558),速度矢量为(单位:m/s)(1 709.450 049,1 426.384 334,3 179.607 804)。待定轨卫星为某颗定点经度为西经100°的GEO卫星,其轨道高度为35 786 km。在J2000.0坐标系下,GEO卫星的初始位置矢量为(单位:m)(218 944.329,42 165 690.224,1 569.712),速度矢量为(单位:m/s)(-3 074.538 892,15.964 294,4.701 927)。
2.2 仿真结果
仿真时间内,与GEO卫星可见的MEO卫星的数量变化如图4所示。

图4 星间可见链路数量变化趋势
对仿真时间内与GEO卫星可见的MEO卫星数量进行统计如下表:
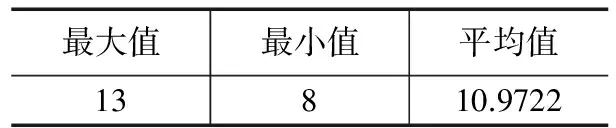
表1 星间可见链路数量统计(条)
对仿真时间内未选星情况下的整体PDOP值进行统计如表2所示。

表2 未选星情况下星座PDOP值变化情况分析
下面给出了不同选星数量和选星策略下所得链路PDOP值的统计情况。

表3 遍历选星时链路PDOP值随选星数量的变化情况分析
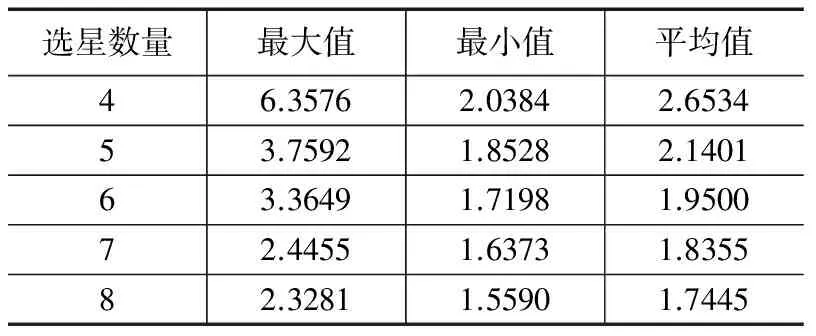
表4 直接选星时链路PDOP值随选星数量的变化情况分析

表5 迭代选星时链路PDOP值随选星数量的变化情况分析
由表2、表3、表4、表5可知,链路PDOP值与选星的数量成反相关,在选星策略一定的情况下,选星数量越多,所得链路构型的PDOP值越小,认为链路构型越优。选星数量较少时,直接选星的会出现偏离最优构型的情况,迭代选星与遍历选星基本上能反映未选星前链路构型变化趋势,得到最优的链路构型。选星数量越多,三种选星策略的选星结果越接近,遍历选星的效果最佳,迭代选星策略次之,然后是直接选星。实际应用中由于卫星载荷视场的限制、可能的轨道机动、大椭圆轨道等原因,建链数不会太多,故以下的分析选星数量均为4。下面将对不同选星算法的选星效率进行分析。

综合考虑选星效果和选星效率,以下仿真分析将以迭代选星算法为例进行实验。仿真分析星间观测存在1m随机误差、动力学模型太阳光压参数存在误差的情况下,选星数量为4、观测频度为5分钟时迭代选星策略下的定轨结果。图5、6分别表示的是未选星情况、迭代选星情况下的定轨结果。
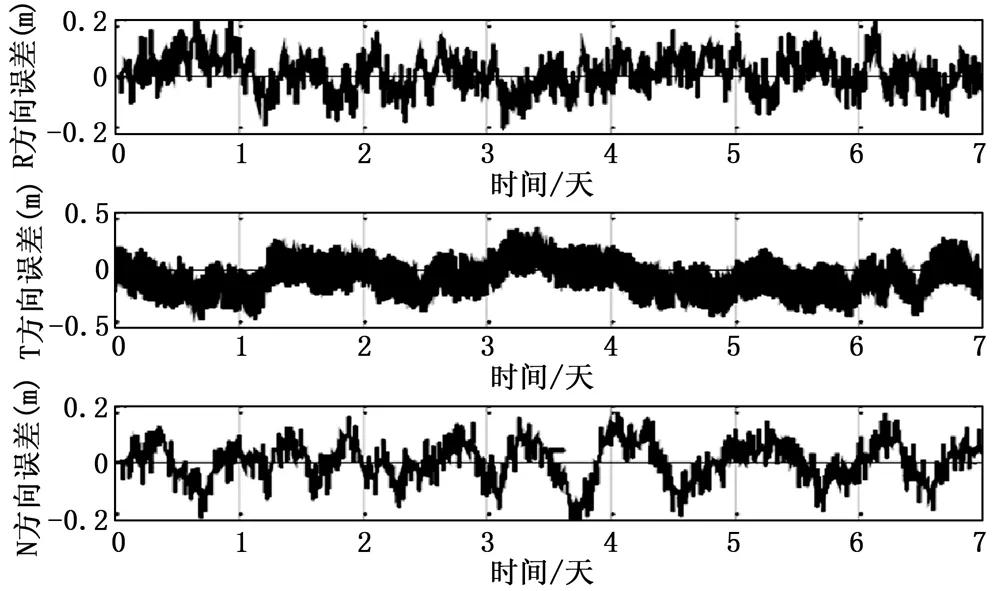
图5 定轨频度为5分钟时未选星情况下的定轨结果

图6 定轨频度为5分钟时迭代选星情况下的定轨结果
由上述结果可知,选星算法能显著提高星间链路资源的使用效率,但是牺牲了一部分定轨精度。为分析链路数量以及观测频度一定情况下的最优定轨精度,下面将以迭代选星算法为例,分析不同链路数量以及观测频度下的GEO卫星的定轨性能。当选星数量为4时,GEO卫星的轨道确定结果如图所示,图7、8、9依次代表的是观测频度为30分钟,60分钟、120分钟时的定轨结果。
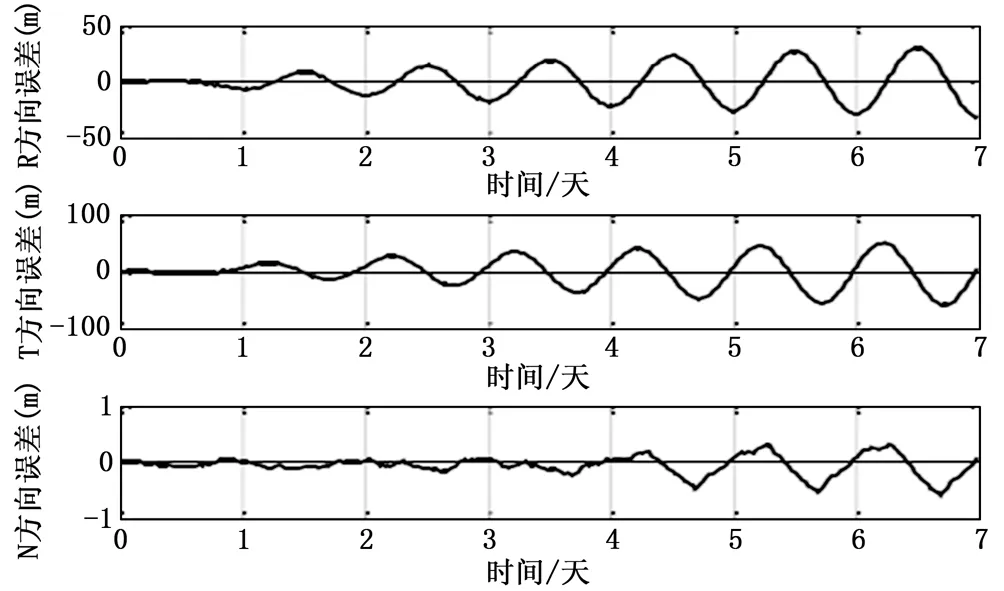
图7 定轨频度为30分钟时迭代选星情况下的定轨结果

图8 定轨频度为60分钟时迭代选星情况下的定轨结果
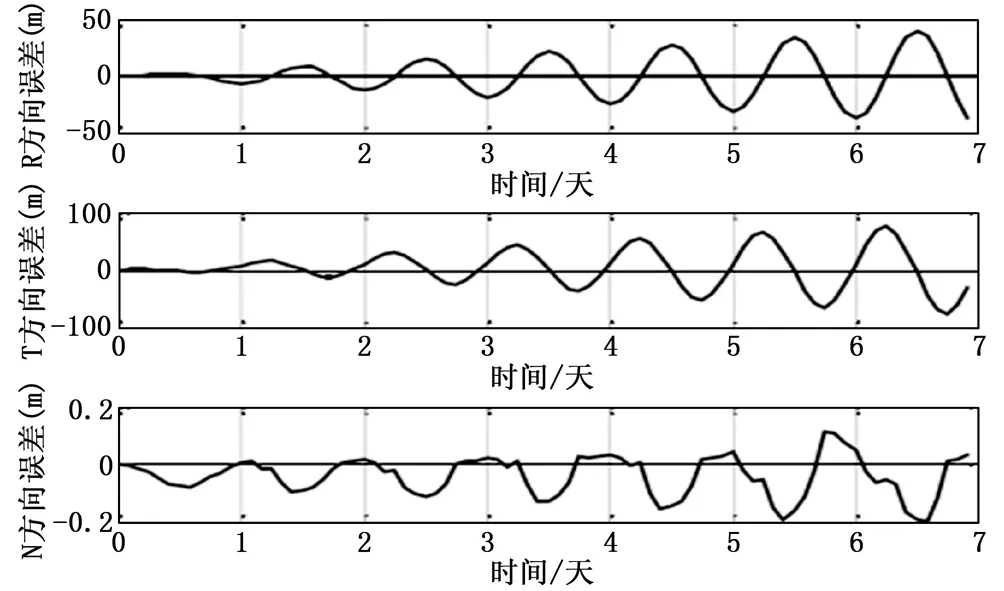
图9 定轨频度为120分钟时迭代选星情况下的定轨结果
相应定轨结果如表6所示。
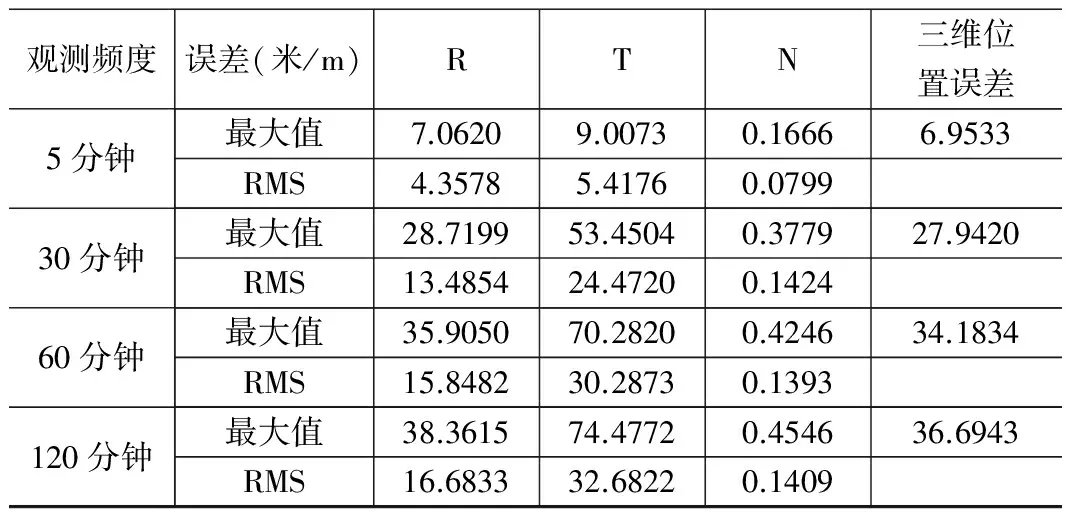
表6 不同观测频度下GEO卫星定轨结果统计
由表6可以看出,星间观测存在米级随机误差、GEO卫星存在动力学模型误差情况下,选星数量为4时,当观测频度为5分钟时,轨道确定误差维持在7米以内;当观测频度为30分钟、60分钟、120分钟时,运用迭代选星策略可将GEO卫星的定轨误差维持在40米以内,且观测越频繁,精度越高。
3 结论
由上述仿真分析可知,文章提出的三种选星策略中,从定轨精度和计算效率来说,迭代选星策略效果最佳,不仅能得到较优的链路构型,而且能提高链路资源的利用率。仿真实验中,仅用4条星间链路,就能将GEO卫星的定轨精度维持在7~40 m以内,同时将星间链路的使用效率提高5~120倍。
参考文献:
[1] 刘 林.航天器轨道理论[M]. 北京:国防工业出版社,2010.
[2] 杜 兰.GEO 卫星精密定轨技术研究[D].西安:解放军信息工程大学,2010.
[3] 谭述森.北斗运行控制策略[A].北京:第一届中国卫星导航学术年会[C].CSNC 2010,2010.
[4] 帅 平.导航星座优化设计与自主导航技术研究[D].北京:中国空间技术研究院博士后流动站,2005.
[5] 俞杭华,何贇晟,周世宏.导航星座的覆盖特性和定位精度因子分析[J].GNSS World of China, 2010,10(3):30-34.
[6] 刘会杰,张乃通.基于 GDOP 的最优定位星座性能研究[J].2010,11(4):32-37.
[7] Kaplan. GPS 原理与应用[M].北京:电子工业出版社,2007.
[8] 帅 平,曲广吉.卫星导航定位方程的病态条件 [J] .飞行器测控学报 ,2006,25(3):1-5.
