基于AR和PSO_SVR的故障趋势预测

, ，2

(1.四川大学 电子信息学院，成都 610065； 2.电子信息控制重点实验室，成都 610065)

0 引言

故障趋势预测是机械装备预测与健康管理(PHM)[1]领域的一个核心内容，对机械装备关键部件进行准确有效的预测是保证保障关键设备安全可靠运行的关键。目前故障趋势预测是通过分析机械设备在使用过程中产生的具有时间序列特征的数据，来推测故障的发展过程。由于机械设备在运行过程中，其状态参数的变化往往是非线性、非平稳的，对于这类非线性时间序列数据，文献[2]使用神经网络非线性的特点来对轴承设备进行故障趋势预测，但神经网络结构存在结构难以确定、需要大量样本、易陷入局部极小等特点。文献[3]采用支持向量机的方法来推测轴承的故障发展趋势，但其输入数据的维度是根据经验来选取，不具有说服力。文献[4]采用自回归滑动平均(Auto-Regressive and Moving Average Model，ARMA)方法，该方法将自回归模型与滑动平均模型结合来对时间序列数据进行预测，但其参数确定比较麻烦。文中将自回归模型(Auto-Regressive，AR)模型和PSO_SVR算法相结合，使用AR模型将非平稳数据平稳化，并确定SVR算法训练数据的输入维度，随后利用SVR对非线性数据进行拟合。

1 AR_PSO_SVR模型

AR_PSO_SVR模型主要包含两个方面：(1)AR模型定阶(2)PSO_SVR模型预测[5]。

1.1 AR模型定阶

1.1.1 数据平稳化

经典的回归模型是建立在平稳数据的基础上，对非平稳数据进行回归会出现伪回归等问题，因而首先要对数据进行平稳性校验。目前最常用的校验方法有DF校验和ADF校验，它们都是通过检验是否存在单位根来检验时间序列的平稳性。其中ADF校验是对DF校验进行了扩充， ADF检验的原理如下：

对于AR(P)过程，如果其特征方程的所有特征根都在单位圆内，则序列{xt}平稳，如果有一个特征根Φ存在且为1，则序列平稳，且自回归系数之和切好等于1。因此，对于AR(P)过程可以通过检验自回归系数之和是否等于1来检验序列的平稳性。作如下假设检验：

H0:：ρ=0↔H1：ρ<0

其中：

ρ=Φ1+Φ2+…+Φp-1

(1)

对于非平稳序列，常用的是差分处理，以下所有的讨论都是基于平稳化的时间序列。

1.1.2 确定模型阶数

AR模型建立首先要确定模型的阶数，当模型阶数较高时，模型预测的结果就比较逼近真实值，但模型阶数的增高时则模型参数的随之增大，因而又会使预测误差增大。故应综合考虑两方面，确定一个合适的阶数。

目前常用的模型定阶的方法有很多，如F准则，FPE准则，AIC准则等。文中使用AIC准则等。AIC是衡量统计模型拟合优良性的一种标准，由日本统计学家赤池弘次在1974年提出，它建立在熵的概念上，提供了权衡估计模型复杂度和拟合数据优良性的标准。通常情况下，AIC定义为：

AIC=2K-2ln(L)

(2)

其中:K是模型参数个数，L是似然函数。从一组可供选择的模型中选择最佳模型时，通常选择AIC最小的模型。

1.2 PSO_SVR模型

1.2.1 SVR算法介绍

按药害分级的方法给每个小区药害定级打分。1级：水稻生长正常，无任何受害症状；2级：水稻轻微药害，药害少于10%；3级：水稻中等药害，以后能恢复，不影响产量；4级：水稻药害较重，难以恢复，造成减产；5级：水稻药害较重，难以恢复，造成明显减产或绝产。于施药后5d、10d、15d、20d、分别记录药害症状，调查水稻株高，调查分蘖数。

对于训练样本数据集(x1,y1),(x2,y2),...,(xl,yl)，其中xi∈Rn作为输入，yi∈R作为输出，则SVR预测的最优化问题为：

(3)

线性SVR可以通过引入核函数K(x,x′)推广到高维空间中，通过求解下面的优化问题在高维空间中构造决策超平面：

(4)

(5)

对应的决策函数形式为:

(6)

1.2.2 PSO优化SVR参数

对于SVR，不敏感损失系数、惩罚系数C、核函数及其参数的优化选择对回归模型的学习精度和推广能力的好坏起着决定性的作用。PSO算法是基于种群的一种搜索策略，没有很多参数需要调整，且收敛速度快，在处理高维问题上有一定的优势[6]。因而文中使用PSO优化SVR模型的参数C(惩罚系数)、g(核函数参数)、p(损失函数参数)，提高其学习精度。

1)初始化参数，确定粒子群的大小以及算法的最大迭代次数；

2)计算每个粒子的适应度，选取当前适应度最好的粒子作为初始全局的最优值；

3)更新粒子的速度与位置；

4)计算当前种群粒子的适应度，选取最优的粒子与全局最优进行比较，选其中的较优值作为新的全局最优值。

5)判断是否达到迭代条件，若否，则跳转到继续执行；若是，则停止。

1.3 AR_PSO_SVR预测模型

对于时间序列{x1,x2,...,xn}，{xn}为预测值，首先使用AR模型判断时间序列的平稳性，其次确定AR的模型的阶数m,该阶数作为SVR学习样本的输入维数。构造输入x={xn-1,xn-2,...,xn-m}，对应输出y={xn}的映射关系：Rm→R,则SVR的学习样本如下：

(7)

(8)

回归函数为：

(9)

AR_PSO_SVR模型用于滚动轴承趋势预测的整体流程如图1所示。

图1 AR_PSO_SVR模型流程图

2 实验数据分析

2.1 实验数据来源

文中使用的实验数据是由美国辛辛那提大学智能系统维护中心提供的滚动轴承全寿命周期加速轴承性能退化实验数据。该数据的采样时间间隔是10分钟，采样频率是20 kHz,采样点数为20 480个，图2是轴承运行后期的一个振动信号幅值图。

图2 轴承振动信号幅值图

2.2 特征提取

滚动轴承的原始信号数据量比较庞大且含有大量的噪声，为了提高预测的准确度，需要对获取的全寿命数据进行特征提取[7-9]，参考文献[10]中的方法提取时域与频域指标共29个，具体的时域特征指标如表1所示，频域特征如表2所示。

表1 时域特征

表2 频域特征

2.3 PCA降维

由于提取的指标不统一且存在一定的冗余性，为有效的提取特征量，需要对特征向量通过主成分析(Principal Component Analysis，PCA)进行降维。PCA是一种将多个指标归结为线性无关的少数主成分的降维技术，这些主成分能够反映原始变量的绝大部分信息，他们通常表示为原始变量的线性组合[11]。更主要的是经过PCA降维后的数据去除了噪声。根据主成分的特征值的方差贡献率，选取PCA主成分最大的一个特征量来检验AR_PSO_SVR模型的预测效果，该主成分的趋势如图3所示。

从图中可以看出在700点之前，特征的信息变化较小，此时轴承处于正常运行阶段，700点以后提取的特征值发生了较大的变化，反映出了轴承的退化趋势。因此选取700点到900点作为训练数据，901点到920点作为预测数据。

3 实验结果分析

为了检验AR和PSO_SVR模型的预测效果，使用AR模型以及PSO_SVR模型与其进行对比。选用均方根误差MSE、绝对平均误差MAE以及决定系数R2作为评价指标来评价预测效果。图4为原始数据与AR_PSO_SVR模型预测值的比较图。

(10)

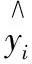
图4中第一个图是使用训练好的模型对训练数据进行回判得到的结果与实际值进行比较，从图中可以看出二者的结果比较吻合，回判的MSE值是0.0028，R2值为0.9701。第二个图是对测试数据进行预测得到的结果与实际值进行比较，预测的MSE值为0.0117，R2为0.8276。

图5比较AR_PSO_SVR模型和AR模型以及PSO_SVR模型的效果，从图中可以看出AR模型的预测曲线和原始曲线相比不够平滑，有很多拐点；单独使用PSO_SVR模型的预测趋势和原始趋势相比误差较大；AR_PSO_SVR模型的预测效果较好。各个模型的各项指标如表3所示。AR_PSO_SVR模型预测的MSE、MAE和R2值均低于AR模型和PSO_SVR模型，其中R2值较AR模型和PSO_SVR模型分别提高了25.89%和53.83%。这些数据表明文中使用模型的预测效果较好。

图4 原始数据与文中模型预测值比较

图5 各种模型预测值比较

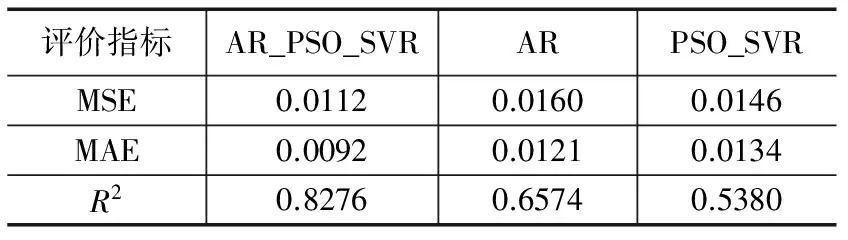
表3 种模型预测误差对比

4 结论

文中分析了AR模型定阶和PSO_SVR模型的基本理论以及AR_PSO_SVR模型的构建。将AR_PSO_SVR模型用于滚动轴承的故障趋势预测。提取滚动轴承的时域和频域特征，同时使用PCA对提取的特征进行降维处理。最后将AR_PSO_SVR模型的预测结果与AR和PSO_SVR模型的预测结果进行对比，实验结果表明文中使用模型的各项指标均优于AR和PSO_SVR模型。虽然AR_PSO_SVR模型在故障预测的单步预测中效果较好，但当进行多步迭代预测时就会因为误差的不断积累，而造成预测结果偏差较大的情况，在后续的研究中可以寻找解决办法提高多步预测的正确率。

参考文献：

[1] 曾声奎, Michael G. Pecht, 吴际. 故障预测与健康管理(PHM)技术的现状与发展[J]. 航空学报, 2005, 26(5):626-632.

[2] 韩昕锋, 任立坤. 基于神经网络的轴承故障预测模型[J]. 海军航空工程学院学报, 2015(3):281-285.

[3] 左 红, 顾家铭, 于锦禄. 基于支持向量机的滚动轴承故障诊断研究[J]. 轴承, 2008(8):36-39.

[4] 朱晓乐, 王 华, 符菊梅,等. 基于ARMA模型的动力系统缓变数据故障趋势预测[J]. 载人航天, 2011, 17(2):54-58.

[5] 任海军, 孙瑞志, 刘广利. 基于AR_SVR模型的时间序列预测算法的研究[J]. 计算机工程与设计, 2010, 31(2):421-424.

[6] 熊伟丽, 徐保国. 基于PSO的SVR参数优化选择方法研究[J]. 系统仿真学报, 2006, 18(9):2442-2445.

[7] 孙 建. 滚动轴承振动故障特征提取与寿命预测研究[D]. 大连：大连理工大学, 2015：13-18.

[8] 王建利.滚动轴承性能退化评价与趋势预测研究[D].大连：大连理工大学, 2013.

[9] 万书亭, 吴美玲. 基于时域参数趋势分析的滚动轴承故障诊断[J]. 机械工程与自动化, 2010(3):108-110.

[10] 董绍江. 基于优化支持向量机的空间滚动轴承寿命预测方法研究[D]. 重庆：重庆大学, 2012.

[11] 范明明. 基于主成分分析的多变量混沌时间序列预测研究[D]. 大连：大连理工大学,2006.