带有滑动边界的可压缩磁流体方程解的局部存在性

陆 剑， 雍 燕

（上海理工大学 理学院，上海 200093）

1 问题的提出

考虑可压缩磁流体方程

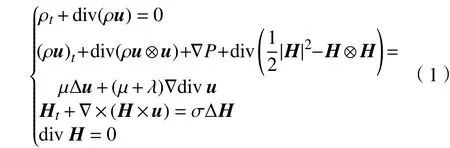
且

所以，磁流体方程（1）中的第3式可写为

磁流体方程是流体力学中的经典模型[1-2]。磁流体方程问题解的存在性是人们关心的一个重要问题。众多学者研究了磁流体方程柯西问题解的适定性。Bian等[3]研究了全空间非等熵可压缩磁流体方程在临界Besov空间上的局部适定性；Kozono等[4]研究了3维可压缩非等熵磁流体方程的柯西问题弱解的全局存在性；Liu等[5]研究了具有某些限制初值的3维可压缩磁流体方程的全局弱解问题。

但是，对于初边值问题，情况变得更加复杂。事实上，在流体力学中，主要考虑两种边界条件：一种是Dirichlet边界条件，；另一种是由Navier提出的著名滑动边界条件，

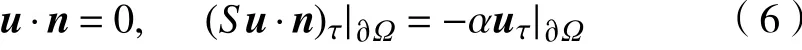
式中：为上的单位外法向向量；是的切向向量，是应变张量；

现对问题（1）～（3），研究其解的局部存在性问题。一般讨论的解有3种。第1种解是光滑小解[6-8]，在这种情况下，初值和解接近于中的某个常数，后来将这个解推广到齐次Besov空间。首先将方程组线性化，然后对线性方程组进行迭代，得到一组逼近解，证明逼近解的渐近衰减速率，最后将逼近解取极限，得到原方程组解的存在性。这类光滑小解是连续可微的，并且大大降低了对初值的限制。缺点是不能体现出Navier-Stokes方程组自身的奇性。第2种解是由Lions提方程的解会出现问题。相反地，出的一般“大能量”弱解[9]，这类解的好处是对任意大的初始能量和非负密度都容易证明解的存在性。但是，这一类解的集合比较大，通常还包含了非物理解。由于这类解的光滑性不够，因此，对解的性质分析起来比较困难[10-11]。第3种解是Hoff解。对于Hoff解而言，优点是它保持了解的非线性和物理上关心的一些有意义的特性。另外，这类解当初值具有足够的正则性时，解一般也具有较好的正则性，可以根据相关定理来证明解的唯一性和连续性[12-14]。比如，当初值是分段光滑函数时，文献[15]中的解在逐点意义下满足Rankine-Hugoniot条件。另外，这些解有足够的正则性，使得解的唯一性和连续依赖性理论可以得到证明[16]。这种解在整个空间中适定性理论几乎是完全成立的，但是，对Dirichlet边界条件：在如果考虑上面提到的Navier-Slip边界条件，那么，对于具有小能量的初值和有界的初始密度来说，可以证明其解的局部存在性。

David[17]研究了等熵Navier-Stokes方程

如果满足边值条件：

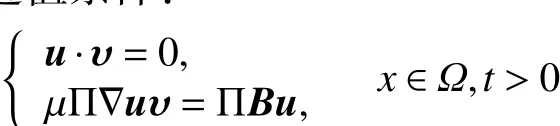
式中：是在上的单位外法向量；是切平面到上的投影。

David证明了解的局部存在性。

本文考虑的是磁流体方程，因为，磁场和流体耦合在一起，研究起来要比Navier-Stokes方程困难，如何处理磁场是解决问题的困难之一。

5 磁流体方程组解的局部存在性

首先考虑磁流体方程组的线性化方程

了。因为，，类似于连续性的证明，可知成立，根据椭圆的正则性理论，可知。

综上，定理1得证。

参考文献：

[1]DAVIDSON P A. An introduction to magnetohydrodynamics[M]. Cambridge, England： Cambridge University,2016.

[2]SERMANGE M, TEMAM R. Some mathematical questions related to the mhd equations[J]. Communications on Pure and Applied Mathematics, 1983, 36(5)： 635-664.

[3]BIAN D F, GUO B L. Well-posedness in critical spaces for the full compressible mhd equations[J]. Acta Mathematica Scientia, 2013, 33(4)： 1153-1176.

[4]KOZONO H. Weak and classical solutions of the twodimensional magnetohydrodynamic equations[J]. Tohoku Mathematical Journal, 1989, 41(3)： 471-488.

[5]LIU S Q, YU H B, ZHANG J W. Global weak solutions of 3D compressible MHD with discontinuous initial data and vacuum[J]. Journal of Differential Equations, 2013, 254(1)：229-255.

[6]TAN Z, WANG Y J. Global well-posedness of an initialboundary value problem for viscous non-resistive MHD systems[J]. Mathematics, 2015, 258(7)： 2531-2571.

[7]OHNO M, SHIROTA T. On the initial-boundary value problem for the linearized MHD equations[J].Sūrikaisekikenkyūsho Kōkyūroku, 1998, 1045： 26-44.

[8]MATSUMURA A, NISHIDA T. Initial-boundary value problems for the equations of motion of compressible viscous and heat-conductive fluids[J]. Communications in Mathematical Physics, 1983, 89(2)： 445-464.

[9]LIONS P L. Mathematical topics in fluid mechanics volume 1： incompressible models[M]. Oxford： Oxford University Press, 1996： 10-121.

[10]HOFF D. Existence of solutions to a model for sparse, onedimensional fluids[J]. Journal of Differential Equations,2011, 250(2)： 1083-1113.

[11]HOFF D, SERRE D. The failure of continuous dependence on initial data for the Navier-Stokes equations of compressible flow[J]. SIAM Journal on Applied Mathematics, 1991, 51(4)： 887-898.

[12]HOFF D. Compressible flow in a half-space with Navier boundary conditions[J]. Journal of Mathematical Fluid Mechanics, 2005, 7(3)： 315-338.

[13]HOFF D. Global solutions of the Navier-Stokes equations for multidimensional compressible flow with discontinuous initial data[J]. Journal of Differential Equations, 1997,120(1)： 215-254.

[14]FAN J S, SONG J, NAKAMURA G, et al. Logarithmically improved regularity criteria for the Navier-Stokes and MHD equations[J]. Journal of Mathematical Fluid Mechanics, 2011, 13(4)： 557-571.

[15]HOFF D, SANTOS M M. Lagrangean structure and propagation of singularities in multidimensional compressible flow[J]. Archive for Rational Mechanics and Analysis, 2008, 188(3)： 509-543.

[16]HOFF D. Uniqueness of weak solutions of the Navier--Stokes equations of multidimensional, compressible flow[J]. SIAM Journal on Mathematical Analysis, 2006,37(6)： 1742-1760.

[17]HOFF D. Local solutions of a compressible flow problem with Navier boundary conditions in general threedimensional domains[J]. SIAM Journal on Mathematical Analysis, 2012, 44(2)： 633-650.

[18]TEMAN R. Navier-stokes equations： theory and numerical analysis[M]. New York： North-Holland Publishing Company, 1979.

[19]XIAO Y L, XIN Z P. On the vanishing viscosity limit for the 3D Navier-Stokes equations with a slip boundary condition[J]. Communications on Pure and Applied Mathematics, 2007, 60(7)： 1027-1055.

[20]EVANS L C. Partial differential equations[M]. 2nd ed.American： American Mathematical Society, 2010.