基于ABAQUS的游离磨粒对单晶锗表面冲击作用仿真分析

杨晓京， 冷智毅

（昆明理工大学 机电工程学院，昆明 650500）

单晶锗具有优越的物理和化学性能，被广泛应用于半导体材料、红外光学材料、化工催化剂、医学应用、军事、航天及其他新领域[1]。近年来，单晶锗作为一种新的清洁能源材料，被成功应用于空间太阳能电池领域。同时，单晶锗是一种较脆的材料，抗机械冲击性能较差。

单晶锗的上述应用带动了相关加工技术的发展，对其表面质量要求也愈来愈高，现有的工具接触加工方法难以在单晶锗表面形成高精度的加工表面。由纳米压痕实验[2-3]可知，在压头与单晶锗材料接触过程中单晶锗材料表面会产生脆-塑转变过程，同时，将磨粒尺寸降低到一定程度，脆性材料的冲击磨损变化特性具有塑性材料的特点[4]。综上所述，采用固液两相流方法可使加工作用力控制在单晶锗塑性形变范围内，以得到更好的表面效果，即通过流体湍流作用，利用磨粒对加工表面冲击，实现对脆性材料的高精度表面加工[5-6]。

本文以单颗磨粒冲击单晶锗材料为例，利用ABAQUS有限元仿真软件，以颗粒的不同冲击角度与不同冲击速度为切入点，分析抛光过程中游离的单颗磨粒与被加工表面冲击产生的应力应变大小；单晶锗材料表面各向异性对相同角度冲击造成的残余应力大小产生影响，为单晶锗固液两抛光加工提供参考依据。

1 游离磨粒冲击磨损理论

Finnie[7-8]提出了刚性粒子对塑性材料的冲击磨损机理。单位时间、单位面积内的磨损率表达式为

式中：W为单位时间、单位面积磨损率，kg/（m2·s）；E为磨损量；n为单位时间冲击壁面颗粒个数；A为磨损面积。

磨损量E表达式为

式中：c为有效冲击粒子比例；m为颗粒质量；v为颗粒速度；为切削长度与深度比；为材料塑性流动应力；K为颗粒形状参数（颗粒垂直水平分量比）；表示角度冲击作用。

角度冲击作用的表达式为

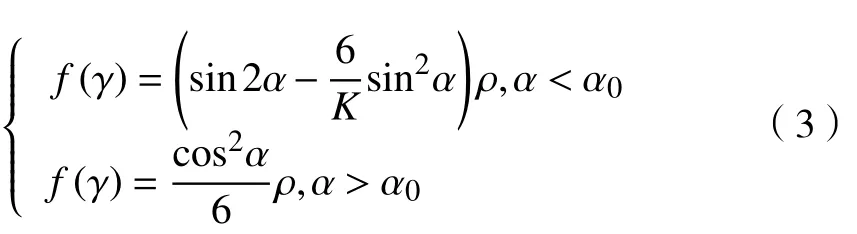
式中：α为颗粒碰撞角度；α0为临界入射角；ρ为加工材料密度。该模型很好地解释了多角形磨粒在小角度冲击情况下对塑性材料的冲击规律，但是对于塑性不典型的材料、大角度冲击、非多角形磨粒的冲击作用误差较大。

Hashish修正了Finnie模型，改进速度指数并考虑材料形状影响。改进后模型为

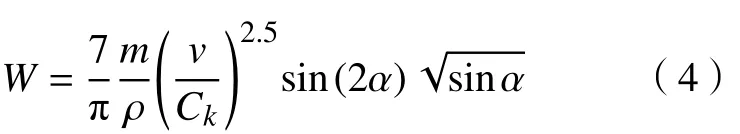
式中：Rf为颗粒圆度因子。

Hashish模型在考虑速度的同时也包含颗粒圆度的影响，该模型适用于塑性材料的冲击磨损情况。

2 磨粒磨损的有限元分析

2.1 有限元分析模型建立

本文建立的有限元模型作如下假设：a. 仅考虑抛光过程中游离颗粒对壁面作用；b. 忽略温度对碰撞作用的影响；c. 颗粒碰撞作用微小；d. 忽略碰撞时由于壁面形变在其他方向上产生的各向异性影响。

本研究利用ABAQUS仿真软件对球形颗粒冲击单晶锗壁面过程进行建模仿真。磨粒与加工壁面分别采用显示三维应力单元C3D10M和隐式线性减缩单元C3D8R，针对冲击接触区间进行加密处理，确保结果精确可靠。

有限元单元实体网格划分如图1所示，加工壁面有22 320个有限元单元，磨粒有1 378个有限元单元。本次仿真被加工材料的模型是对称模型，故采用模型的一半进行建模分析以减少计算时间，加工材料尺寸为 500 μm×250 μm×60 μm。在现实加工过程中所使用的磨粒尺寸很小，为方便单颗磨粒对加工材料表面冲击仿真的过程与结果进行更直观的研究, 减少由于网格过于细分造成计算量过大，根据相似性理论本次仿真将颗粒尺寸进行放大[9-10]，球形磨粒尺寸半径为30 μm。磨粒在冲击过程中速度较快, 本文主要研究单晶锗材料的变形过程, 忽略磨粒的变形影响，同时为减少计算时间, 将磨粒约束为刚体。

图1 有限元单元网格划分Fig.1 Finite element mesh

本研究选择的被加工材料为单晶锗，其材料参数如表1所示。冲击磨粒实际使用的材料为SiC，其材料参数如表2所示。单晶锗材料具有力学性能上的各向异性，其弹性模量随受冲击角度不同而变化，弹性模量理论值如图2所示。表1与表2中的ρ为材料密度，E为材料的弹性模量。

表1 单晶锗的材料参数Tab.1 Material parameters of monocrystalline germanium

表2 SiC的材料参数Tab.2 Material parameters of SiC

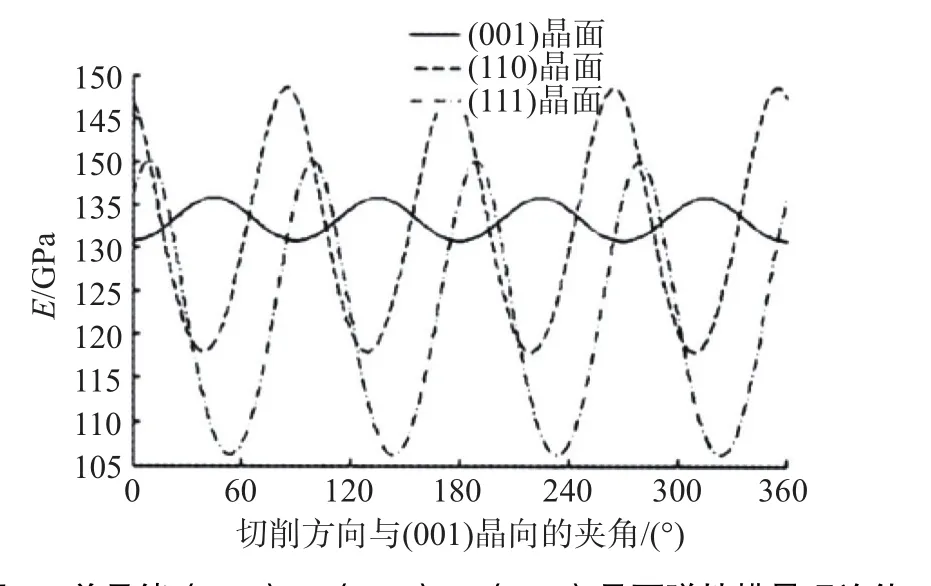
图2 单晶锗（001），（110），（111）晶面弹性模量理论值Fig.2 Theoretical values of modulus of elasticity for single crystal germanium (001), (110) and (111) planes

2.2 有限元仿真结果分析

2.2.1 被加工表面塑性变形分析

在实际的加工过程中，液体项流速必须大于70 m/s才会产生湍流作用。磨粒运动方式复杂，将其自身旋转因素考虑在内会加大仿真运算时间,并对仿真过程研究分析造成一定影响。同时，本文仅考虑磨粒对待加工材料表面冲击的情况，故磨粒的运动形式选择平动[8]。基于上述因素，选择的仿真参数如下：磨粒速度为140 m/s，冲击角度为40°，磨粒与加工表面的接触时间为4×10-6s，单晶锗径向为（111）。

被加工表面的塑性变形过程如图3所示。由图3可知：磨粒与待加工表面接触并产生塑性变形，随着时间推移，接触深度越深塑性变形效果越明显；在磨粒颗粒离开被加工表面后，被加工材料表面塑性变形量保持不变。在单颗磨粒与被加工材料表面接触的过程中，被加工材料表面所受接触应力突然增大至最大值；磨粒离开被加工表面后，在被加工材料表面产生接触应力，呈先快速减小然后缓慢减小至恒定值保持不变的趋势。

冲击的过程中，法向作用力将磨粒压入待加工表面，并在待加工表面产生塑性变形，水平作用力使磨粒与待加工表面产生相对切削作用。在仿真过程中材料变形属于塑性变形, 材料表面不会产生切屑，表面材料仅在磨粒水平作用下沿水平方向堆积。该过程与文献[11]所认为的“材料磨粒磨损是由于金属表面发生微观切削作用，相对滑动时磨粒对表面产生犁刨作用，在加工表面形成磨损”观点一致，也与计时鸣等[8]仿真观察结论相一致。在实际加工过程中，多速度方向的磨粒对同一位置进行多角度的冲击，被加工材料表面经上述两种作用力的作用，产生的塑性变形面积不断增加。经过多颗磨粒的反复作用，达到对单晶锗材料表面高精度加工效果。2.2.2 不同速度冲击作用分析

为分析不同冲击速度作用下，单颗磨粒冲击待加工表面产生的应力变化趋势与应变大小，本文将半径为30 μm的单颗磨粒冲击速度分别设置为 80，100，120，140，150，160 m/s，冲击角度为40°，磨粒的运动方式选择为平动。经ABAQUS仿真后，所得在各个速度条件下的时间-应力曲线如图4所示；磨粒离开材料表面后不同速度下材料应变效果如图5所示。

由图4（a）可以看出，接触应力随速度增大呈先增大后减小趋势，其中临界值为120 m/s。冲击速度小于120 m/s时，单颗磨粒在被加工材料表面产生的接触应力随磨粒速度增加而增大。由图4（b）可知，当冲击速度大于120 m/s时，单颗磨粒在待加工材料表面产生最大接触应力随速度增加而缓慢减小。120 m/s冲击造成单晶锗材料微小塑性变形应力大小接近材料屈服极限值，因此120 m/s时最大应力值最大；当速度大于120 m/s时，磨粒冲击所产生的应变量处于该材料变形过程中的屈服阶段，因此当速度大于120 m/s时，该速度下为达到最大应变，所需要的最大应力值反而减小。同时，达到最大应力值所需时间呈先逐步增加后保持不变的趋势，100 m/s为临界值。当速度小于100 m/s时，达到最大应力值所需的时间随速度增加而逐步增加；当速度大于100 m/s时，速度大小不影响达到最大应力值所需时间，即达到最大应力值所需的时间均相同。

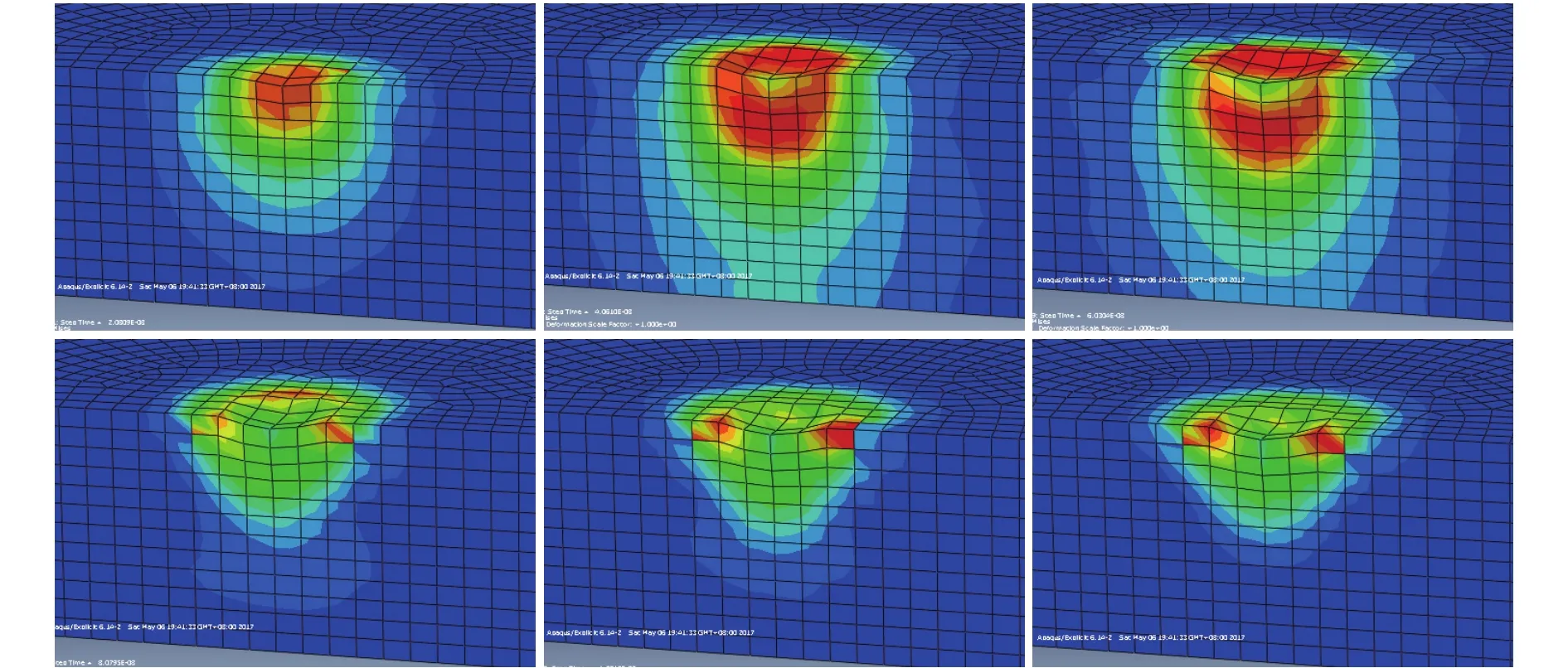
图3 材料表面塑性变形过程Fig.3 Process of plastic deformation on material surface

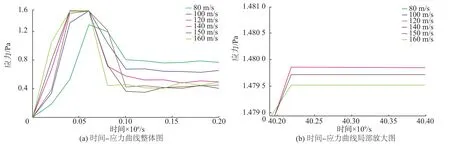
图4 时间-应力曲线图Fig.4 Time-stress graph

由图5可知，随磨粒速度增加，磨粒在待加工表面造成的变形量增大。磨粒初始动能随磨粒初始速度增大而增大，磨粒和材料表面接触时，可用来与材料交换的能量相对增多，因此，随磨粒速度增加，磨粒在待加工表面可造成更大的变形。当速度较小时磨粒初始动能较小，磨粒冲击工件表面发生微小弹性变形，冲击产生应力未达到材料屈服极限，不能造成明显塑性变形。随着磨粒速度增加，磨粒初始动能增大，冲击材料表面时，可造成更大的法向方向塑性变形与切线方向材料堆积，从而产生较大的塑性应变。结合图4和图5可知，单颗磨粒冲击待加工材料产生的最大接触应力不影响被加工材料表面产生的塑性变形量，但影响材料表面残余应力范围大小。磨粒速度影响冲击产生的塑性变形量。

2.2.3 不同角度冲击作用分析

单晶锗材料是一种具有各向异性的脆性材料，因此，在仿真过程中不能忽略由于冲击角度不同产生的单晶锗材料表面力学性能各向异性现象。单晶锗材料各向异性一般是指其剪切模量和弹性模量的各向异性，单晶锗的弹性模量E随晶向变化，关系如式（5）所示，弹性模量E的变化曲线如图2所示[12-13]。

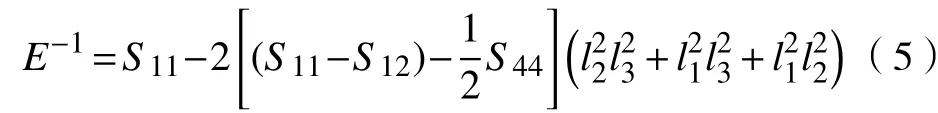
式中：li为晶向与晶格坐标系的方向余弦；S1i为单晶锗的柔度系数。

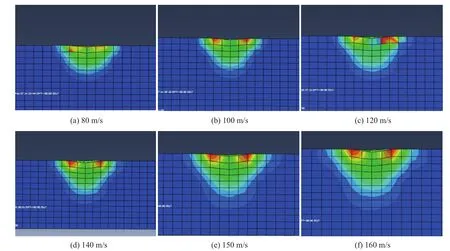
图5 材料应力应变图Fig.5 Stress and strain diagram of material

本文将半径为30 μm的单颗磨粒的冲击速度设置为140 m/s，冲击角度分别设置为30°, 45°,60°, 90°，建立了上述4个冲击角度下单晶锗材料所对应的理论弹性模量仿真模型，分析不用角度冲击作用下，单颗磨粒冲击被加工材料表面产生接触应力变化的趋势及应变大小。经ABAQUS仿真后，所得在各角度条件下的时间-应力曲线图如图6所示；磨粒离开材料表面后所产生的应变效果如图7所示。

由图6（a）可知，当单颗磨粒以140 m/s的速度从不同角度冲击后，在较短时间内应力会突然增加到最大值后逐渐减小至一个恒定值，当速度角度为90°时，最大应力值会保留一段时间后再缓慢减小。由图2可知，单晶锗的理论弹性模量值在这4个角度均不相等，大小关系为：90°时弹性模量大于30°时弹性模量；30°时弹性模量大于45°时弹性模量；45°与60°时的弹性模量值接近。通过图6（b）可知冲击造成的最大接触应力大小为：90°冲击作用产生应力大于45°冲击作用产生应力；45°冲击作用产生应力大于30°冲击作用产生应力；30°冲击作用产生应力大于60°冲击作用产生应力。不同冲击角度引起的单晶锗材料弹性模量各向异性仅影响冲击产生的最大接触应力值，达到最大接触应力值所用时间相同。弹性模量较大的材料变形所需的能量相对较大，因此，90°产生的最大接触应力最大，60°产生的接触应力最小。45°条件下游离磨粒对被加工材料表面法向作用力大于30°条件下的法向作用力，由于脆性材料法向作用力是产生塑性变形的主要影响因素，因此45°条件下产生的最大接触应力大于30°条件下产生的最大接触应力。

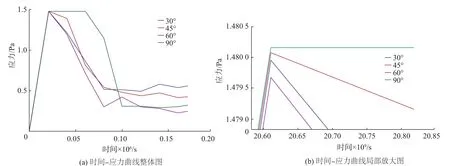
图6 不同角度下的时间-应力曲线图Fig.6 Time-stress graph under different degrees

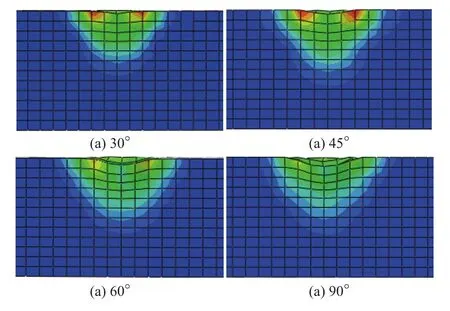
图7 不同角度下材料应力应变图Fig. 7 Stress and strain diagram of material under different degrees

图7 为不同角度下材料应力应变图。由图7观察可知，90°冲击作用下变形最明显，60°冲击作用变形效果次之。结合图7和图2可知，由于单晶锗材料冲击角度不同，引起单晶锗材料表面弹性模量的各向异性对冲击作用造成的塑性变形量没有影响。由图7可知，冲击角度影响材料表面是否产生应力集中现象和被加工材料表面塑性变形量大小：当冲击角度越大，法向作用越明显，在材料表面也以塑性变形为主，应力集中现象也会消失；随冲击角度增大，单颗磨粒在待加工材料表面造成变形量增加。因此，在实际加工过程中，为获得较好的表面质量、较快的加工速度，应将磨粒冲击角度控制在90°附近。

3 结 论

a. 利用ABAQUS软件进行有限元分析，进行单颗磨粒冲击待加工材料的仿真可观察到：冲击过程中，随着游离磨粒与被加工材料接触加深，材料表面产生的应力瞬间增加至最大值；当游离磨粒离开材料表面后，游离磨粒产生的接触应力先快速减小、后缓慢减小至恒定值。

b. 可直观地观察到单颗磨粒在水平与法向作用力作用下，造成被加工材料表面法向方向塑性变形、水平方向材料堆积。在实际加工过程中，经过多颗磨粒在同一位置的反复作用，达到对加工的单晶锗材料表面精密加工的效果。

c. 不同冲击速度作用下，游离磨粒在材料表面造成最大接触应力以速度值120 m/s为临界值，随速度增加呈先增大后减小的趋势；达到最大应力值所需时间以100 m/s为临界值，所需时间随速度增加呈先增加后不变的趋势；磨粒与材料接触所产生的最大接触应力不影响塑性变形量大小，仅影响在材料表面产生的残余应力大小。

d. 不同冲击角度作用下，由于冲击角度不同，引起单晶锗材料力学性能各向异性，影响最大接触应力值，不影响材料变形量；随着冲击角度增大，材料受冲击后在表面产生的应力集中现象会逐渐消失，材料表面塑性变形量增加。

参考文献：

[1]宣宁. 锗： 新材料骄子[J]. 中国金属通报, 2010(30)：14-19.

[2]杨晓京, 刘艳荣, 杨小江, 等. 单晶锗各向异性力学性能实验[J]. 农业机械学报, 2014, 45(5)： 322-326.

[3]赵研. 冰冻固结磨料抛光单晶锗薄片的机理与工艺研究[D]. 南京： 南京航空航天大学, 2015.

[4]石成霞. 冲击载荷作用下材料塑性变形实验研究[D]. 青岛： 青岛理工大学, 2010.

[5]KUROBE T, YAMADA Y, YAMAMOTO K.Development of high speed slurry flow finishing of the inner wall of stainless steel capillary： polishing and gas flow characteristics of various size of capillaries[J].Precision Engineering, 2001, 25(2)： 100-106.

[6]JAIN V K, ADSUL S G. Experimental investigations into abrasive flow machining (AFM)[J]. International Journal of Machine Tools and Manufacture, 2000, 40(7)：1003-1021.

[7]FINNIE I. Erosion of surfaces by solid particles[J]. Wear,1960, 3(2)： 87-103.

[8]计时鸣, 王嘉琦, 谭大鹏. 基于ABAQUS的单个颗粒与加工面碰撞对固液两相流加工的影响研究[J]. 机电工程,2013, 30(1)： 1-4.

[9]王嘉琦. 固-液两相磨粒流中对于颗粒碰撞结构化表面的研究[D]. 杭州： 浙江工业大学, 2012.

[10]李艺. 游离磨粒加工中流场的数值模拟与实验研究[D].湘潭： 湘潭大学, 2007.

[11]全永昕, 施高义. 摩擦磨损原理[M].杭州： 浙江大学出版社, 1992.

[12]夏晓光. 锗单晶超精密加工各向异性的影响研究[D]. 昆明： 昆明理工大学, 2014.

[13]陈洪荪. 金属的弹性各向异性[M]. 北京： 冶金工业出版社, 1996.