基于Parareal算法的电磁暂态时间并行计算方法
2018-05-22汪芳宗
汪芳宗 胡 洁
(三峡大学 电气与新能源学院, 湖北 宜昌 443002)
0 引 言
近年来,随着能源互联网、微电网的发展,各种新型电力电子装置被接入电网,电力系统变得愈发复杂[1-5].电磁暂态仿真适用于分析电力系统暂态特性,是电力系统的设计、规划和控制运行的理论基础.面对日益复杂的电力系统,如何快速又准确地对系统进行电磁暂态仿真计算一直是国内外学者们研究的重点问题.
目前大多数电磁暂态数值计算方法基本上是基于传统的串行计算模式,难免会出现效率低的问题.并行算法为解决这一问题提供了一个很好的技术途径.并行算法一般可分为:空间并行算法、时间并行算法和时空并行算法.广泛应用的并行算法大多为空间并行算法,例如长输电线路解耦法、多端口戴维南等值电路法[6-8]、类似节点分裂法的分网并行方法[9]等.在进行大规模电力系统暂态数值计算时,空间并行算法不可避免地会因为网络分块数目的增多,而使得各子网间通信量增大,通信延时变高[10].另外,网络分割不均匀也会产生系统计算负荷不均、计算资源浪费的情况.时间并行计算为避免上述情况提供了一种有效的思路.
电磁暂态数值仿真本质上是求解微分动力学方程在时间域上的响应.文献[11-16]中介绍了几种求解微分方程的时间并行算法,其中最受到关注的是Lions等人提出的Parareal算法和Gander提出的Paraexp算法.Paraexp算法计算效率高,主要用于计算线性方程,当电磁暂态数值仿真中存在大量非线性方程时,Paraexp方法的使用便受到了限制.
Parareal算法可用于计算非线性方程.该方法计算过程简单且收敛速度快,可应用于时间依赖性问题的并行计算.本文将Parareal并行算法应用于电磁暂态数值仿真中,以提高电磁暂态数值计算的效率.
1 Parareal算法介绍
考虑微分方程初始值问题:
(1)
式中,f:RM→RM且x:R→RM.
将时间窗Ω=(0,T)分成N个子区间,每个子区间可表示为Ωn(Tn,Tn+1),n=0,1,…,N-1,且ΔTn=Tn+1-Tn.考虑每个子区间的求解问题:
(2)
式中,Xn表示状态变量x在Tn时刻的精确解,在每个子区间Ωn内必须严格满足式(1).
(3)
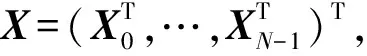
(4)
F:RM·N→RM·N,式中下标为时域子区间,Xn为每个子区间待求的初始值,用牛顿迭代法求解该系统:
(5)
式中,上标k表示迭代次数,JF表示雅各比矩阵,牛顿迭代亦可写成式(6)的形式:
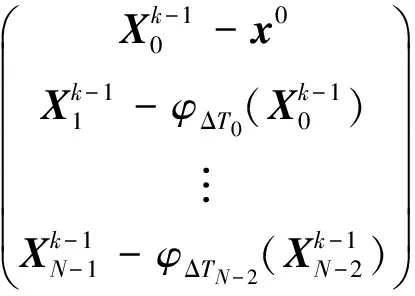
(6)
则有
(7)
其中n=1,…,N-1.式(7)是二次收敛,收敛速度很快.然而事实上,对于非线性方程来说,计算其雅各比矩阵,会耗费大量时间和计算机内存.Parareal算法为解决这一问题提供了一种有效技术途径.定义两种运算:F(Tn,Tn-1,Xn-1)表示通过数值算法F求得子区间Ωn内φΔTn-1(Xn-1)的精细解;G(Tn,Tn-1,Xn-1)表示通过数值算法G求得各时间点Tn=n×ΔT时刻φΔTn-1(Xn-1)粗糙解,它可以采用更大的计算步长、低阶的数值方法甚至一种更为简单的模型计算得到.式(7)中各部分可近似表示为:
(8)
因此式(7)可表示为式(9)的格式:
(9)
综上所述,Parareal算法的计算步骤可描述如下.为简单起见,将G(Tn,Tn-1,Xn-1)和F(Tn,Tn-1,Xn-1)简写成G(Xn-1)和F(Xn-1).图1为Parareal迭代过程示意图.
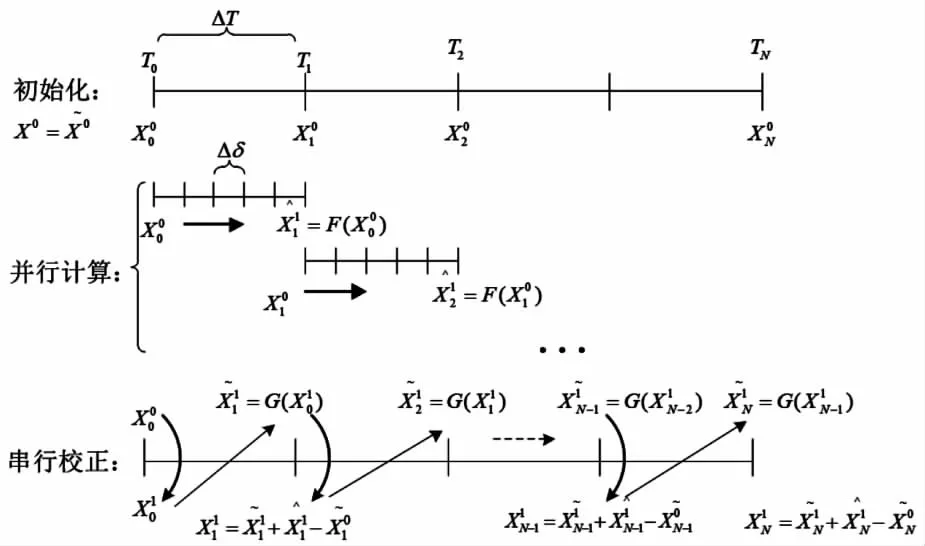
图1 Parareal迭代过程
1)通过数值算法G采用大步长ΔT求取状态变量x在各时间点Tn=n×ΔT上一组初始解:
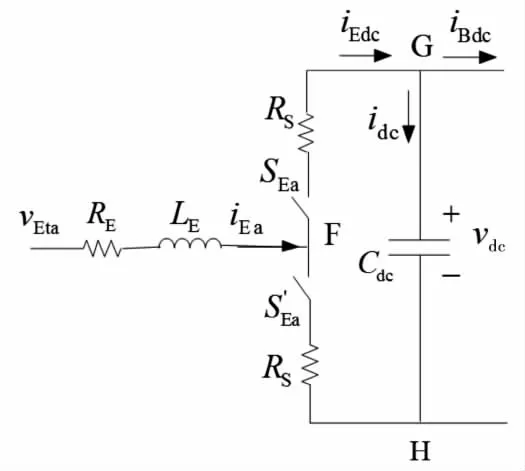
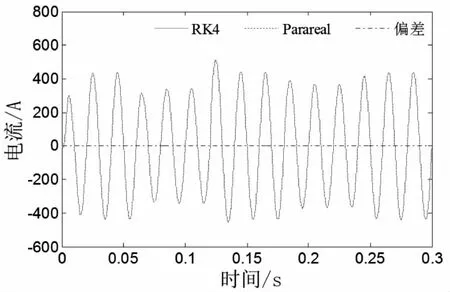
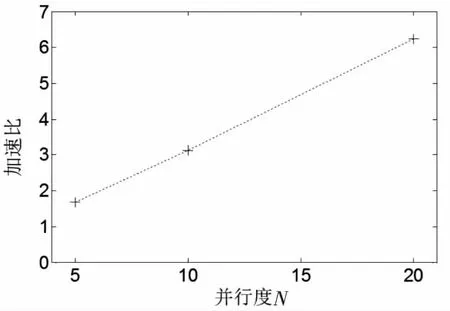
∀1≤n (10) 2)通过数值算法F采用小步长Δδ在每个子区间Ωn=[Tn-1,Tn)单独且同时进行计算: (11) 3)执行串行校正: (12) FACTS(flexible AC transmission system)因其快速调节的特性被广泛应用于电网.统一潮流控制器(unified power flow controller,简称UPFC)由变压器和换流桥组成的并联侧和串联侧通过直流电容耦合而成,是FACTS技术中一种最典型、最完整的装置.因此,对UPFC暂态特性的研究很有意义. 图2为UPFC的简化结构图,mE、δE为并联换流器的调制比和触发角,mB、δB为串联换流器的调制比和触发角,均由控制系统给出,VE和VB分别为并联侧和串联侧电压. 对上述系统做如下假设: ①换流桥由理想阀元件组成,其正向漏电流为0. ②系统电压为工频正弦波,系统三相平衡. 以并联侧电路为例(串联侧同理),其a相等值电路如图3所示. 图2 UPFC简化结构图 图3 a相等值电路图 (13) (14) 式中,RE、LE分别为并联侧每相桥臂的等效电阻和电感,Rs为开关电阻,vEta和iEa分别为UPFC并联侧a相交流电压和电流,vFa和vHn分别为F点和H点的电压. (15) 系统三相平衡,则有 (16) 用开关函数在一个开关周期内的基本波形dEj和dBj来代替SEj和SBj (17) (18) (19) 式中,vEtj和vBtj分别为UPFC并联侧和串联侧的每相交流电压,iEtj和iBtj分别为UPFC并联侧和串联侧的每相交流电流,j=a,b,c.vdc为直流侧电压,Cdc为直流电容,交流侧时域动态模型: (20) 直流侧时域动态模型: (21) 上述系统中UFPC参数为:并联侧电压为170 V,串联侧电压为10 V,系统频率50 Hz,RE=0.1 Ω,RB=0.1 Ω,LE=500 μH,LB=500 μH,Cdc=1 mH,RS=0 Ω(忽略开关阻抗).t=0.06 s时,并联侧调制比mE由0.3阶跃到0.7,串联侧调制比mB由0.6跳变到0.3,二者均在t=0.12 s时恢复初始值,t=0.18 s时,给并联侧电压施加扰动,其值从初始的170 V下降到140 V,然后在t=0.24 s时恢复初始值,总仿真时长0.3 s. 图4~6分别是采用Parareal算法并行计算与4阶Runge-Kutta算法串行计算得到的结果.Parareal并行算法中,大步长ΔT取1 ms,采用隐式梯形法进行初始值预估;小步长Δδ取0.1 ms,子区间内并行计算方法采用4阶Runge-Kutta算法. 图4 并联侧a相电流 图5 串联侧a相电流 图6 直流侧电压 表1是算法收敛性测试结果,图7是在不同的并行度N下,Parareal算法相对于传统串行算法获得的加速比曲线.加速比是衡量Parareal并行算法性能的重要指标.当加速比大于1时,表示该算法的计算速度优于传统串行计算,加速比越大,则该算法计算效率越高.从图7可以看到,随着并行度的增大,加速比也在增大,当并行度为20时,加速比可达到6.25. 表1 算法收敛性测试结果 图7 加速比曲线 Parareal算法处理非线性方程时,具有过程简单、收敛速度快的优点,其收敛速度已被证明为超线性收敛.将Parareal并行算法应用于电磁暂态数值仿真计算中,算例结果表明该方法并行度高,可获得有效的加速比,在提高电力系统电磁暂态数值仿真速度方面效果显著.理论上,当使用大量处理器时,该算法可以获得的仿真计算速度与电力系统实际动态过程一致. 参考文献: [1] 邹延生,董萍.一种基于协同控制的SVC新型非线性控制器[J].电力系统保护与控制,2017,45(5):10-17. [2] Gholipour E,Saadate S.Improving of Transient Stability of Power Systems Using UPFC[J].Power Delivery IEEE Transactions on,2005, 20(2):1677-1682. [3] Márquez J L,Molina M G,Pacas J M.Dynamic Modeling, Simulation and Control Design of an Advanced Micro-hydro Power Plant for Distributed Generation Applications[J].International Journal of Hydrogen Energy,2010,35(11):5772-5777. [4] 王帅兵,李 琳,谢裕清,等.统一潮流控制器中串联耦合变压器特性及仿真模型研究[J].电网技术,2017,41(2):551-557. [5] 黄宇鹏,汪可友,李国杰.基于权重数值积分的电力电子开关仿真插值算法[J].电网技术,2015,39(1):150-155. [6] Marti J R,Linares L R,Calvino J,et al.OVNI:an Object Approach to Real-time Power System Simulators[C]// International Conference on Power System Technology, 1998.Proceedings.Powercon.IEEE,1998:977-981 vol.2. [7] Tomim M A,Mart? J R,Wang L.Parallel Solution of Large Power System Networks Using the Multi-Area Thévenin Equivalents (MATE) algorithm[J].International Journal of Electrical Power & Energy Systems,2009,31(9):497-503. [8] 王成山,李 鹏,王立伟.电力系统电磁暂态仿真算法研究进展[J].电力系统自动化,2009,33(7):97-103. [9] 岳程燕,周孝信,李若梅.电力系统电磁暂态实时仿真中并行算法的研究[J].中国电机工程学报,2004,24(12):5-11. [10] 宋炎侃,陈 颖,黄少伟,等.大规模电力系统电磁暂态并行仿真算法和实现[J].电力建设,2015,36(12):9-15. [11] Gander M J,Güttel S.PARAEXP:A Parallel Integrator for Linear Initial-value Problems[J].Siam Journal on Scientific Computing,2013,35(2):C123-C142. [12] Gander M J,Vandewalle S.On the Superlinear and Linear Convergence of the Parareal Algorithm[J].Lecture Notes in Computational Science & Engineering,2007,55:291-298. [13] Fabozzi D,Chieh A S,Haut B,et al.Accelerated and Localized Newton Schemes for Faster Dynamic Simulation of Large Power Systems[J].IEEE Transactions on Power Systems,2013,28(4):4936-4947. [14] Scala M L,Brucoli M,Torelli F,et al. A Gauss-Jacobi-Block-Newton Method for Parallel Transient Stability Analysis of Power Systems [J].IEEE Transactions on Power Systems,1990,5(4):1168-1177. [15] Gurrala G,Dimitrovski A,Pannala S,et al.Parareal in Time for Fast Power System Dynamic Simulations[J].IEEE Transactions on Power Systems,2016,31(3):1820-1830. [16] Martin J.Gander,Stefan Vandewalle.Analysis of the Parareal Time-Parallel Time-Integration Method[J].Siam Journal on Scientific Computing,2007,29(2):556-578.2 电磁暂态计算
2.1 算例模型

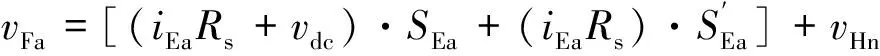
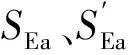


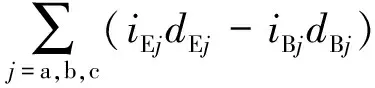
2.2 算例测试结果



3 结 论
