复杂地质条件下堆积体边坡稳定性及其敏感性分析
2018-05-22沈桑桑卢晓春蒋建伟
沈桑桑 卢晓春 蒋建伟
(1.三峡大学 水利与环境学院,湖北 宜昌 443002;2. 三峡大学 土木与建筑学院, 湖北 宜昌 443002)
崩塌堆积体其主要变形破坏模式主要包括边坡表面石块滚动、沿边坡内部滑动、沿原河谷岸坡滑动.主要表现为多层面和复杂性,地质勘测不能确定其危险滑动面;若单一地依据地质勘测确定其危险滑动面也不符合安全性评价要求.故本文通过采用基于有限单元法的ABAQUS软件进行三维计算来确定崩塌堆积体的危险滑动面.同时堆积体物质来源为上部花石崖危岩体边坡的崩塌物,以及冲沟两岸岸坡崩塌物,堆积体的物质形状会随着时间推移而变化,导致其力学特性参数无法确定.力学参数又对最终安全计算结果与评价具有重要影响,故本文通过参数敏感性分析为确定力学参数提供依据.
1 工程概况
根据金沙水电站枢纽工程布置及地质勘察报告,金沙水电站坝址区及近坝库段的不良地质主要有横贯枢纽上、下游右岸导流明渠边坡的2号挠曲体(包括牛筋树堆积体及2号挠曲体)、上游右岸的花石崖危岩体及其下覆的崩塌堆积体等.
花石崖崩塌堆积体边坡较陡,坡角30°左右,以粗颗粒的块石为主,前缘伸入江内,厚度大,重心低;蓄水后前缘被淹高度12 m,受库水浸泡和冲刷等作用可能会产生局部滑塌.如发生大面积滑坡或大落差崩塌,轻则将影响施工期左岸施工场区的安全,阻塞河道,形成堰塞湖;同时塌滑体入江引起的涌浪将直接危及大坝在施工期安全及运行期水电站的安全高效运行,产生一系列的次生灾害.重则将冲毁建筑物及设备,造成严重的经济损失,甚至造成大量人员伤亡.故对崩塌堆积体进行稳定性分析必不可少.
2 计算方法
2.1 材料本构关系[6]
1)材料屈服准则
考虑到岩石材料抗拉、抗剪能力较弱的特点,本研究中岩石材料采用最大拉应力和Mohr-Coulomb准则相结合的判断准则.当材料产生受拉破坏时,采用最大拉应力准则,即
F1=σ1-Rt=0
式中,Rt为抗拉强度.
当材料产生剪切破坏时,采用Mohr-Coulomb准则,材料的应力状态达到下列极限时,材料屈服,即:
|τ|=c-σtanφ
式中,τ为最大剪应力,σ为作用在同一平面上的正应力,c为材料的凝聚力,φ为材料的内摩擦角.
2)材料的应力应变关系
基于Mohr-Coulomb准则,计算中岩石被视为理想弹塑性材料,其应力应变关系分为两个阶段,第一阶段为弹性变形阶段,第二阶段为塑性变形阶段.单向受力时,当应力小于屈服极限σs时,材料处于弹性阶段;当应力达到σs时,材料即进入塑性状态.然而在复杂应力状态条件下,材料的某一点产生塑性变形时,应力也必须满足复杂应力状态下的屈服条件.一般来说,屈服条件是6个应力分量的函数,可表示为:
F(σx,σy,σz,σxy,σyz,σzx)=C
式中,C为与材料有关的常数,F为屈服极限.将某点的6个应力分量带入上式,如果F 建立在极限平衡原理基础上的刚体极限平衡方法的基本原理为:1)在分析滑坡的受力和变形过程中,忽略滑体的内部变形,认为滑体为不可变形刚体;2)假定滑体处于极限强度状态;3)在考虑稳定安全系数后,滑体在所受各种荷载的作用下处于平衡状态;4)在计算分析中,将滑坡体分为若干竖向土条.由于对土条分界面上的作用力作出的简化和假定不同,出现了各种计算分析方法[7]. 在这里对于花石崖崩塌堆积体沿原河谷边坡滑动破坏模式的刚体极限平衡分析采用的分析方法主要为Morgenstern-Price法.Morgenstern-Price首先对任意曲线形状的滑裂面进行了分析,导出了满足力的平衡及力矩平衡条件的微分方程式,然后假定两相邻土条法向条间力和切向条间力之间存在对水平方向坐标的函数关系,根据整个滑动土体的边界条件求出问题的解答. 3.1.1 计算模型建立 为了计算花石崖崩塌堆积体的应力状态,本文采用基于有限单元法的ABAQUS软件建立了其对应的有限元计算模型,计算模型如图1所示. 图1 花石崖崩塌堆积体及山体三维网格示意图 在计算模型的建立中,主要基于以下原则来确立计算模型: 1)严格按照实际地形建模:根据地形地质图,在建立计算模型时考虑了实际地形特性; 2)考虑崩塌堆积体材料分区:为精确模拟崩塌堆积体的应力状态,在建立有限元计算模型时考虑了崩塌堆积体的材料分区; 3)合理网格数量划分:在满足计算精度的条件下尽量提高计算效率,本计算模型采用渐变的网格划分方法.计算模型的单元类型为C3D4,整个模型包括66 641个结点,348 538个单元,其中崩塌堆积体包括12 199个结点,56 368个单元. 在计算中主要考虑堆积体自重、降雨以及地震等作用. 计算边界条件采用理想约束条件.其中模型底部边界面上的节点受X、Y、Z3个方向约束,沿着河道方向两端的节点受X方向约束,垂直于河道方向两端仅受Y方向约束. 3.1.2 计算参数 经过钻孔勘察实验,崩塌堆积体的堆积物质为大块石夹碎石岩屑、冲积物,以块石、漂石为主,夹少量卵石、砾砂与碎石土.依据相关地勘资料及力学试验成果,初步确定计算所采用各地层的主要物理力学参数见表1. 表1 花石崖崩塌堆积体各土体的物理力学参数建议值表 3.1.3 计算工况 由于目前堆积体边坡已经形成,为了确保在工程建设过程中以及今后电站建成后的长期运行中的边坡的安全,需要分析施工期水位、正常蓄水位和校核洪水位下的崩塌堆积体边坡稳定性.作用在该崩塌堆积体边坡上的主要荷载有边坡自重,降雨荷载以及地震荷载.根据水位、荷载组合等情况一共设计6个计算工况,见表2. 表2 崩塌堆积体边坡计算工况 注:3种特征水位分别为施工期水位998.21 m,水库蓄水后正常蓄水位1 022 m以及校核洪水位1 025.3 m. 3.1.4 计算结果分析 由于计算工况较多,一共6个工况,而且每种工况下有限元计算可提供的结果较多,本文仅整理施工期水位(工况2)、正常蓄水位(工况1)和校核洪水位(工况4)下堆积体在自重作用下的应力应变规律.崩塌堆积体的位移场在其自身形成的过程中同样逐渐完成,但是考虑到崩塌堆积体在自重荷载下的位移场可以评估其运动趋势,为其稳定性分析提供参考,因此,在该计算过程中保留了崩塌堆积体在自身自重荷载下的位移场. 1)工况1(正常蓄水位+自重),如图2~4所示. 2)工况2(施工水位+自重),如图5~7所示. 3)工况4(校核洪水位+自重),如图8~10所示. 图2 堆积体顺河向位移图(单位:m) 图3 堆积体垂直河流向位移图(单位:m) 图4 堆积体竖向位移图(单位:m) 图5 堆积体顺河向位移图(单位:m) 图6 堆积体垂直河流向位移图(单位:m) 图7 堆积体竖向位移图(单位:m) 图8 堆积体顺河向位移图(单位:m) 图9 堆积体垂直河流向位移图(单位:m) 图10 堆积体竖向位移图(单位:m) 从上述各工况组合下崩塌堆积体边坡的应力场与位移场可知(U1为顺河流方向位移,U2为垂直河流向位移,U3为竖向位移): 1)由于该边坡是由原河谷岸坡山体上方的危岩体崩塌坠落,在原河谷岸坡上堆积而成,该崩塌堆积体边坡在自重荷载作用下会有沿原河谷岸坡滑动的趋势,会形成竖向位移分量和垂直于河流向的位移分量,同时自重荷载会使边坡本身下沉,表现为竖向位移.具体的位移分布规律还受地形特征、水位及不同荷载组合的影响. 2)从崩塌堆积体边坡竖向位移分布图可知竖向位移在数值上大于垂直河流向位移和顺河流向位移,且最大竖向位移均发生在崩塌堆积边坡B区的中上部和崩塌堆积边坡A区下部,A区下部的竖向位移在数值上小于B区的中上部的竖向位移;故危险滑动面为B2-B2,如图11所示. 图11 崩塌堆积体B2-B2工程地质剖面图 3)崩塌堆积体边坡垂直河流向位移分布规律呈现两个特点:崩塌堆积体A区与B区的连接处出现较大的垂直河流向位移,因为崩塌堆积体A区的下滑与自身下沉作用会导致连接部位的隆起;崩塌堆积体A区与B区由于下滑会产生垂直于河流方向的位移分量. 4)水位对崩塌堆积体的竖向位移分布规律有较大影响,水位较高的工况如正常蓄水期工况和校核洪水期工况对应的竖向位移最大值较施工期水位对应工况下的竖向位移最大值所处的高程高,且对应的最大位移绝对值也大些. 地质调查及材料室内力学试验在获取材料力学参数时,由于实验样本的随机性以及天然材料与室内材料的差异性,导致计算材料参数不能完全真实反映材料的力学特性.然而,凝聚系数和内摩擦角作为边坡材料的力学参数在边坡稳定性计算中直接决定了边坡的稳定安全系数,故研究材料的凝聚系数和内摩擦角对边坡安全系数的影响十分必要,并为材料参数的确定提供指导. 依照地勘提供的材料参数设计本材料参数敏感性研究方案.由3.1节中确定选取危险滑动面B2-B2剖面为计算研究剖面(如图11所示),分别研究边坡安全系数对凝聚系数和内摩擦角的敏感性.具体而言,分别计算φ=32°、34°、36°时,凝聚系数c分别为0、10、20、30、40、50 kPa时边坡对应的安全系数,以此探究凝聚系数c对边坡安全系数的影响规律;计算凝聚系数c为0、10、20 kPa时,内摩擦角Ф分别为31°、32°、33°、34°、35°、36°、37°和38°时边坡的安全系数,以此探究内摩擦角Ф对边坡安全系数的影响规律. 3.2.1 参数正交试验 图12(a)~(f)为φ=34°时对应凝聚系数c分别为0、10、20、30、40、50 kPa时边坡安全系数值及相应的滑弧位置.统计了φ=32°、34°、36°时对应的敏感性计算结果;图13(a)~(h)为c=0 kPa时对应内摩擦角φ分别31°、32°、33°、34°、35°、36°、37°和38°时边坡安全系数及相应的滑弧位置.统计了c=0、10、20 kPa时对应的敏感性计算结果,见表3,并绘制相关关系图(如图14~15所示). (a) c=0 kPa,φ=34° (b) c=10 kPa,φ=34° (c) c=20 kPa,φ=34° (d) c=30 kPa,φ=34° (e) c=40 kPa,φ=34° (f) c=50 kPa,φ=34°图12 φ=34°时与c的敏感性计算结果 (a) φ=31°,c=0 kPa (b) φ=32°,c=0 kPa (c) φ=33°,c=0 kPa (d) φ=34°,c=0 kPa (e) φ=35°,c=0 kPa (f) φ=36°,c=0 kPa (g) φ=37°,c=0 kPa (h) φ=38°,c=0 kPa图12 c=0 kPa时与φ的敏感性计算结果 安全系数凝聚系数c/kPa0 10 20 30 40 50内摩擦角φ/°311.4141.6881.784321.5261.6921.7851.8721.9592.045331.5591.6961.786341.5261.6921.7851.8731.962.046351.5571.6941.785361.5591.6961.7861.8741.9612.047371.5611.6971.786381.5631.6981.787 3.2.2 计算结果分析 分析图14可知:边坡安全系数与材料的凝聚系数c几乎成线性增长关系,且当凝聚系数c超过10 kPa后不同内摩擦角对应的安全系数完全由凝聚系数c决定.所以此边坡的安全系数对凝聚系数c十分敏感,在测量凝聚系数c时应当谨慎.分析图15可知:内摩擦角φ对该边坡的安全系数影响小,在c=0 kPa时,当内摩擦角增长至35°后再增长就不会再提高该边坡的安全系数,且当凝聚系数c的取值超过10 kPa后,内摩擦角将不再影响该边坡的安全系数.可见该边坡对内摩擦角不敏感. 图14 c值与安全系数Fs关系图 图15 φ值与安全系数Fs关系图 通过危险滑动面和参数敏感性分析,得出以下结论:1)对于复杂三维堆积体边坡,可采用有限元方法计算其应力及变形,得到其危险滑动面.2)对于力学参数不确定的边坡可采用正交试验方法,计算分析其安全性.3)在堆积体稳定性分析中,边坡安全系数对岩石力学参数凝聚力系数c和内摩擦角φ有着较大的敏感性.同时凝聚力系数c和内摩擦角φ的值对滑弧有着明显的影响进而影响安全性.4)对于类似工程,以上方法和结论具有一定的参考性. 参考文献: [1] 江文才,巫锡勇,孙春卫,等.堆积体边坡及危岩体稳定性分析[J].铁道建筑,2018,58(1):121-124. [2] 冯 刚.复杂堆积体边坡变形失稳分析及其稳定性综合评价[D].天津:天津大学,2011. [3] 张楚楚,孙少锐,王 帅,等.马河崩塌体边坡稳定程度敏感性分析[J].河北工程大学学报(自然科学版),2016,33(3):52-56. [4] 莫晓华,赵双祥.基于正交设计的软弱夹层岩质边坡影响因素分析[J].北方交通,2014,10(10):66-68. [5] 王熠琛.土坡地震稳定性影响因素的敏感性分析[D].哈尔滨:中国地震局工程力学研究所,2015. [6] 张克恭,刘松玉.土力学[M].北京:中国建筑工业出版社,2010.188-193. [7] 陈祖煜.土质边坡稳定分析:原理·方法·程序[M].北京:中国水利水电出版社,2003:533-560. [8] 郭明伟,葛修润,李春光,等.边坡和坝基抗滑稳定性分析的三维矢量和法及其工程应用[J].岩石力学与工程学报,2010,29(1):8-20. [9] 邹 烨,郭明伟,王水林,等.地震荷载下三维边坡动力稳定性分析[J].岩石力学与工程学报,2017,36(5):1174-1184. [10] 张楚楚,孙少锐,王 帅,等.雅砻江楞古水电站马河崩塌堆积体边坡稳定性评价[J].三峡大学学报(自然科学版),2016,38(5):41-45.2.2 刚体极限平衡法
3 堆积体边坡计算分析
3.1 危险滑动面的确定
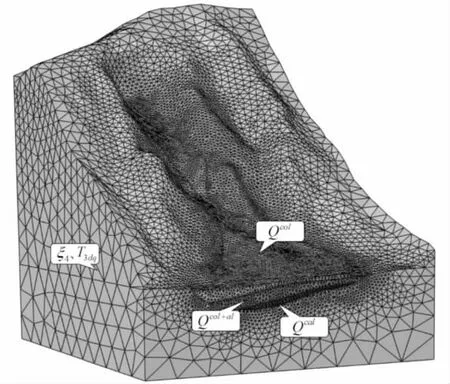
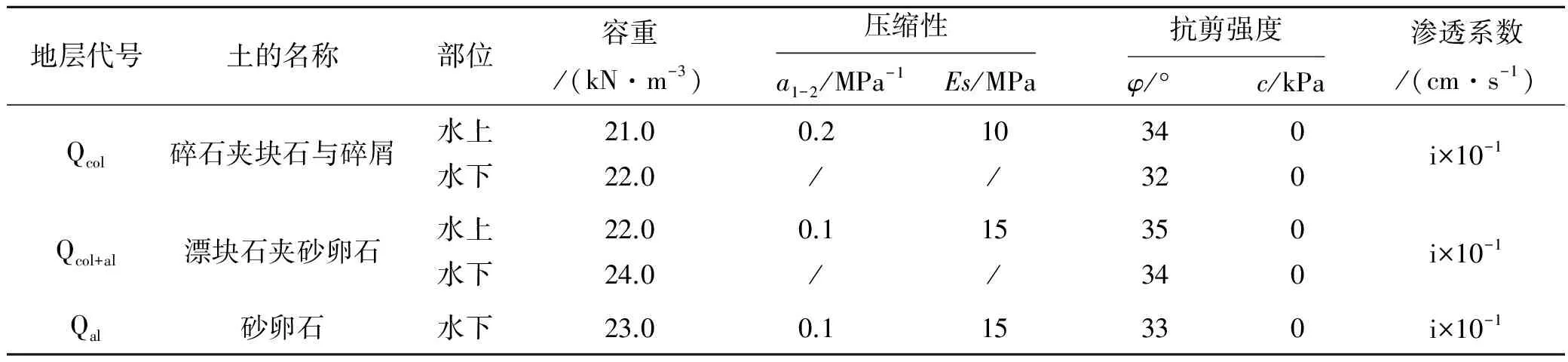

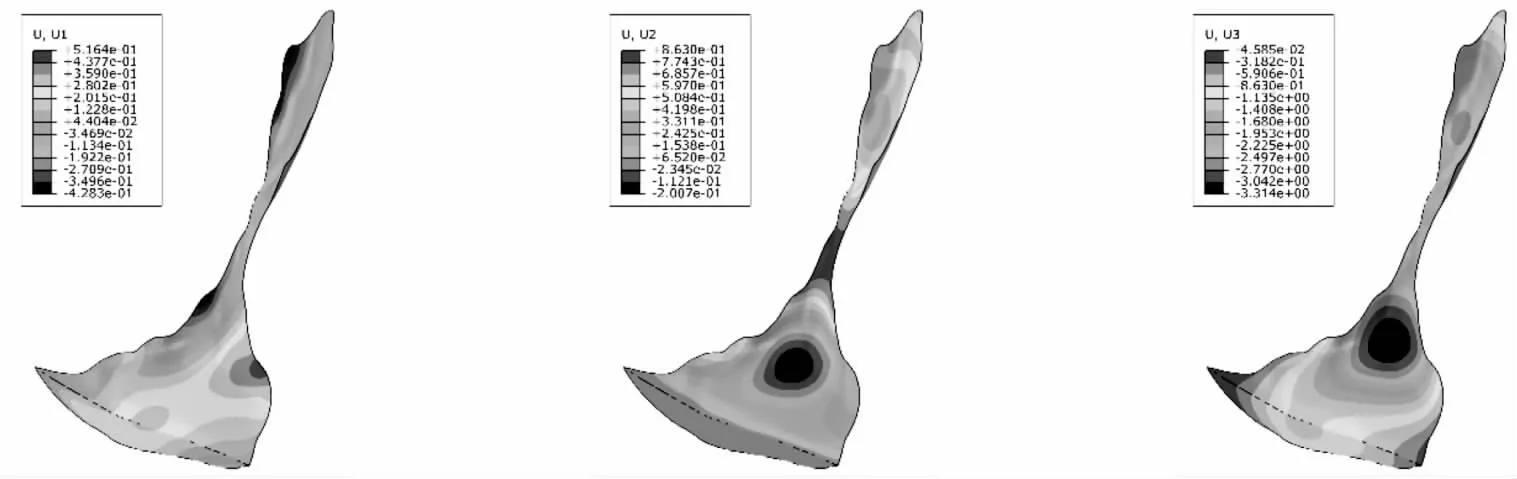

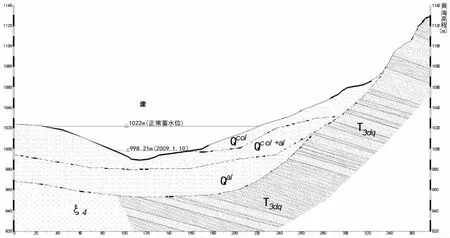
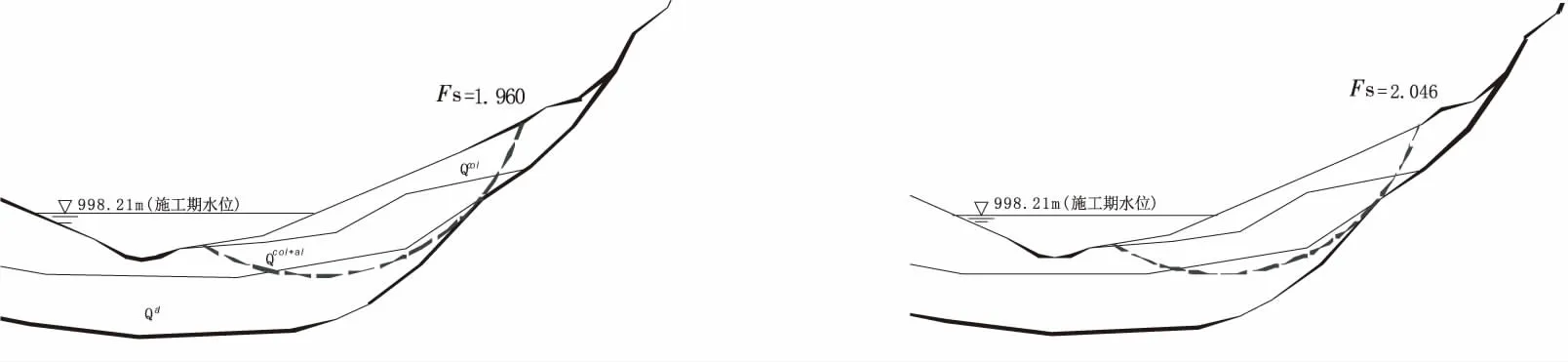
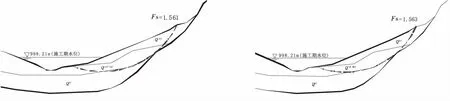
3.2 边坡安全系数影响因素分析





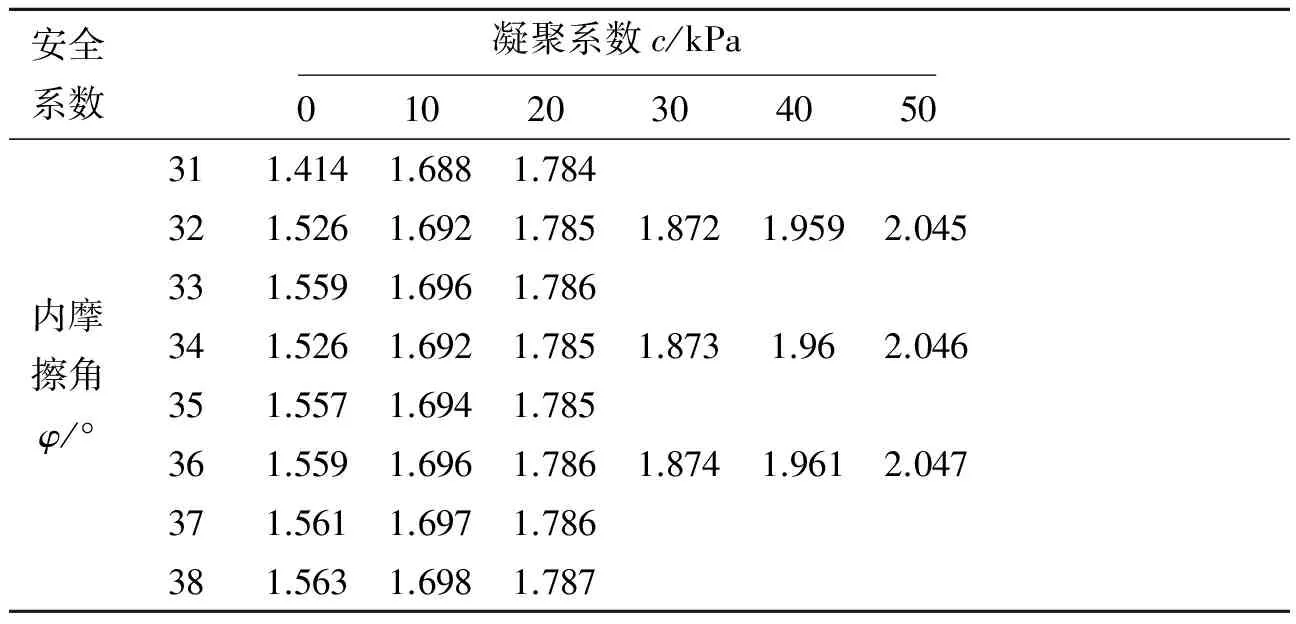
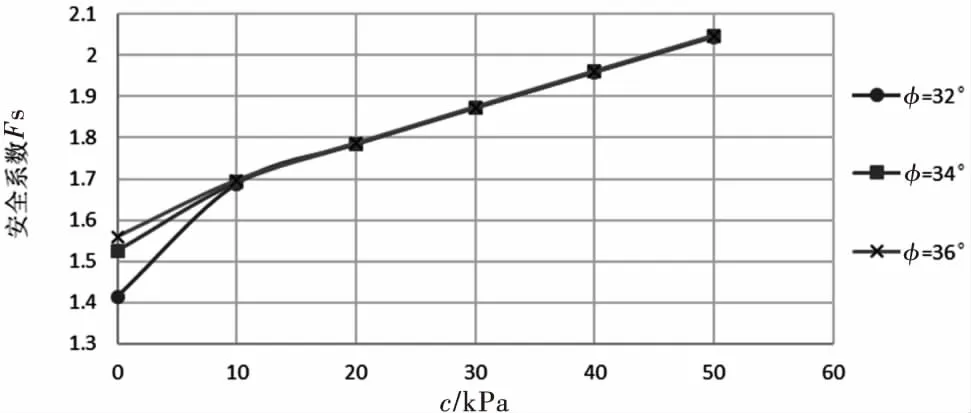
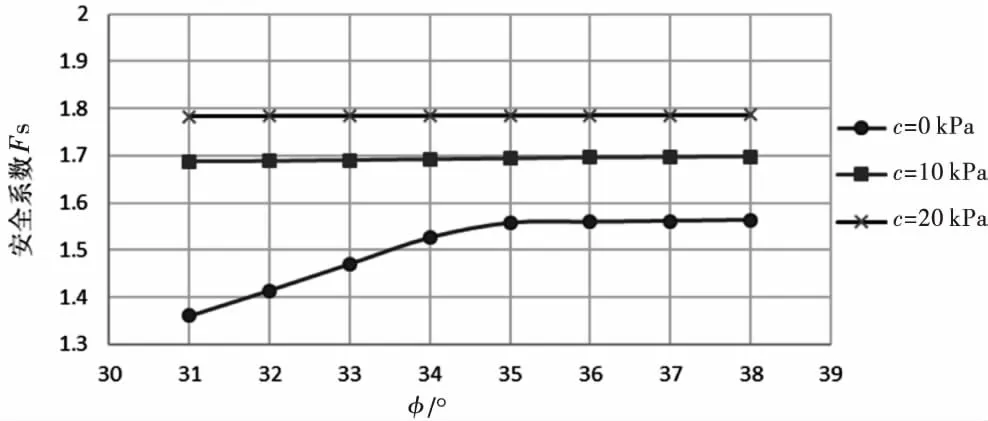
4 结 论
