基于区间直觉模糊集的科技成果转化匹配决策模型

杨 庆，张再生，尤欣赏

（1.山西财经大学 会计学院，太原 030006；2.天津大学 管理与经济学部，天津 300072）

0 引言

进入经济“新常态”发展阶段，创新驱动成为国家重要发展战略，创新创业引领时代浪潮。然而，科技创新创业的快速推进离不开科技资源的有效共享与合理配置。作为科学技术和商业市场之间不可跨越的中间环节，技术成果转化面临着交易签约率不高、技术成果转化不畅等现实问题。何桢等[1]以天津市科技成果转化体系为实证研究对象，发现其有效运作的关键障碍环节为科技成果评价环节与科技成果市场建设环节。汪良兵等[2]研究发现，我国技术转移体系演化态势良好，但总体水平不高，技术中介和扩散系统为其薄弱环节。这些研究都探明了科技服务平台及科技成果转化的宏观影响因素，并提出对策建议。但基于微观视角，采用科学方法探索研究如何建立科学高效的科技资源供需匹配决策机制的研究并不丰富。因此，本文旨在构建科技成果转移匹配优化模型，为促进科技成果成功转化提供借鉴与参考。

1 问题描述

Roth在1985年首次提出了双边匹配的概念[3]，并将其最早应用于婚姻市场中，旨在根据男女双方偏好，使其尽可能找到最佳配偶。随着双边匹配理论与算法的不断发展与演化，经济管理领域的诸多问题也逐渐采用双边匹配方法来进行决策[4-7]。本文将区间直觉模糊集理论引入基于满意度的双边匹配问题，以更贴合现实决策情境，更有效的解决科技成果供需匹配问题。

本文将科技成果供给方主体设为A={A2， ...，Am} ，其中Ai表示供给方的第i个匹配主体；科技成果需求方主体设为其中Bj表示科技成果需求方的第j个匹配主体，并且设同时记科技成果供给主体对于需求方的评价指标集为对应的权重向量为；科技成果需求主体对于供给方的评价指标集为，对应的权重向量为则科技成果供给方主体Ai对于需求方主体Bj关于评价准则uf的满意度矩阵可记为为科技成果供给方主体Ai给出的对于需求方主体Bj考虑评价准则uf的满意度；科技成果需求方主体Bj对于供给方主体Ai关于评价准则vg的满意度矩阵记为为科技成果需求方主体Bj给出的对于供给方主体Ai考虑评价准则vg的满意度。此外考虑到现实中客观事物的复杂性和满意度评价的主观性，科技成果供需主体关于各个评价指标的期望水平与客观实际水平的偏差判断具有模糊性，因此本文中科技成果供给双方给出对方主体的满意度与均为区间直觉模糊数。

2 科技成果转化供需匹配模型构建

2.1 相关概念与理论

定义1：令X为非空论域，D[0 ， 1] 为区间[0，1]的所有封闭子区间，称为区间直觉模糊集，为区间直觉模糊数，如果满足其中分别表示元素x对于集合A的隶属度区间和非隶属度区间，则犹豫度区间可表示为

定义2：称一一映射θ：A∪B→A∪B为双边匹配，当且仅当∀Ai∈A、∀Bj∈B满足以下条件：

（1）θ(Ai)∈B,i∈M

（2）θ(Bj)∈A∪{Bj},j∈N

（3）θ(Ai)=Bj当且仅当θ(Bj)=Ai

定义3：若θ(Ai)=Bj，则称θ(Ai，Bj) 为一一映射θ确定的一组配对，也称其为由θ确定的一个匹配方案；若θ(Ai)=Ai，则称Ai在一一映射θ下未匹配[9]。

定义4：设为一个区间直觉模糊数，定义其得分函数为和精确函数为定义其隶属不确定函 数和 犹 豫 不 确 定 函 数

基于四个函数，Wang[11]给出了比较任意两个区间直觉模糊数的方法：对于任意两个区间直觉模糊数

（1）若S(α)＜S(β)，则α＜β；

（2）若S(α)＞S(β)，则α＞β；

（3）若S(α)=S(β)，则：

①若H(α)=H(β)，则α＜β；

②若H(α)＞H(β)，则α＞β；

③若H(α)=H(β)，则

若T(α)=T(β)，则α＜β;

若T(α)=T(β)，则α＞β；

若T(α)=T(β)

(i)若G(α)=G(β)，则α＜β；

(ii)若G(α)=G(β)，则α＞β；

(iii)若G(α)=G(β)，则α~β。

并且Z.Wang等[11]通过给出定理证明对于任意两个不同的区间直觉模糊数都可以用文献[12]中的定义给予区别：对于任意两个区间直觉模糊数

2.2 模型构建

本文重点解决基于满意度评价的双边匹配问题，用区间直觉模糊数表示匹配科技成果供需双方互相评价结果综合考虑到在比较任意两个区间直觉模糊数时，考虑到定义3和定义4中的四个函数在决策问题中的使用频率，本文给出的函数加权满意度如式（1）和式（2）所示：

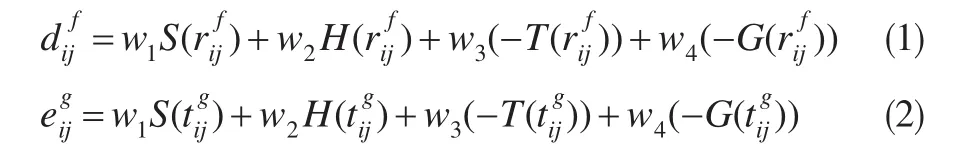
按照判断函数的重要性程度，这里设w3，w4)=(0.4，0.3，0.2，0.1) 。记科技成果供给主体给出的对于需求主体的函数加权满意度矩阵为A(B)=(dij)n×m，其表示科技成果供给方Ai给出的对于科技成果需求方Bj的函数加权满意度，i∈M，j∈N；科技成果需求主体给出的对于供给主体的函数加权满意度矩阵为B(A)=(eij)m×n，其中表示科技成果需求方Bj给出的对于供给主体Ai的函数加权满意度，i∈M，j∈N。

进一步地，考虑供需双方每一个主体对各自一方的满意度的影响，记科技成果供给主体对需求主体的主体加权满意度为：表示科技成果供给方每一个主体Ai，i∈M，所占据的权重；主体对甲方主体的加权满意度为,其中wBi表示科技成果需求方每一个主体Bj，j∈N，所占据的权重，本文中wAi和wBj通常由科技服务平台根据实际决策倾向情况给出。基于匹配双方的加权满意度，可以构建以双方的满意度最大为目标的双目标优化模型M1：

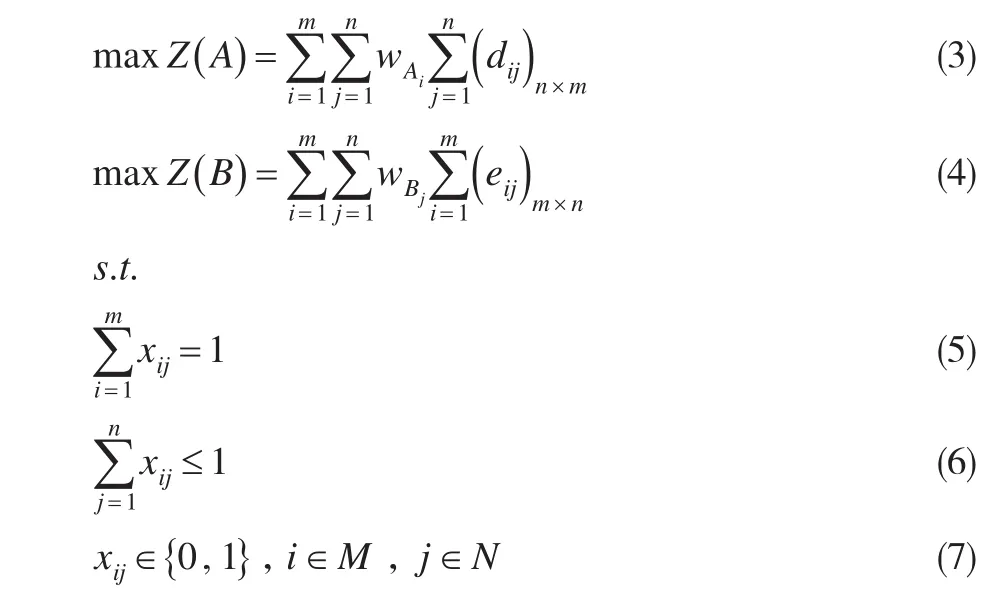
其中xij表示一个0-1变量，xij=0表示θ(Ai) ≠Bj，即Ai和Bj未匹配；xij=1表示θ(Ai)=Bj，即Ai和Bj匹配。

为了求解上述模型，由参考文献[9]可知，同时考虑匹配主体双方满意度的互补性和一致性，比单独仅考虑互补性的线性加权更加合理。因此同时引入算数加权与几何加权，构建如下的单目标优化模型M2：

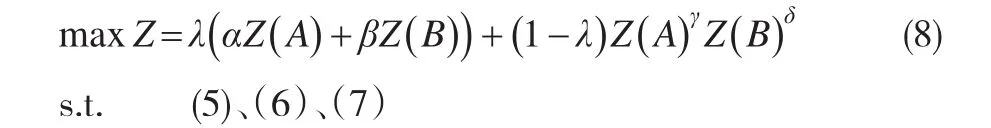
其中α，β分别表示在互补性下科技成果供需主体两方各自的权重，满足α+β=1，γ，δ分别在一致性下供需主体两方各自的权重，满足γ+δ=1。若匹配决策中更加注重匹配双方某一方的满意度，此时就可以根据需要增加该方的权重；而λ表示决策目标函数中双方主体满意度互补性的权重，1-λ则为决策目标函数中双方主体满意度一致性的权重，λ(0 ≤λ≤1)也可根据决策目标的侧重进行相应调整。

2.3 模型求解

由于模型M2为一个含有m×n个变量的0-1整数优化模型，则其至多有2m×n个优化解，并且xij=0，i≠j，xij=1，i=j，i∈M，j∈N是模型M2的一个解，即模型的有效解肯定存在。由多目标规划理论可知，单目标模型M2的最优解是双目标模型M1的有效解。

综上所述，科技成果供需匹配优化模型的应用的主要步骤如下：

第一步：分别确立科技成果供需双方评价指标集及其权重向量wU={

第二步：科技成果供需匹配双方根据评价标准给出满意度矩阵

第三步：根据式（1）和式（2）得到指标加权 满 意 度 矩 阵A(B)=(dij)n×m和B(A)=(eij)m×n，进而得到加权满意度Z（A）和Z（B）。

第四步：将Z（A）和Z（B）代入模型M2，可由软件LINGO 11解得科技成果供需最优匹配方案。

3 实例应用

本文选取天津市某科技成果交易中心为分析案例，该服务平台开展关于科技成果智能匹配、智能推介等服务。据平台统计，技术成果供给方有7家科研院所，记为：；技术企业需求方有 10 家企业，记为：

3.1 技术成果供需双方评价指标体系构建

科技服务平台通过调查问卷了解到技术成果供给方在对需求企业进行选择时，主要考虑交易本身、成果与企业适应性及企业应用能力等方面[1]。结合相关研究，本文将科技成果供给方对需求方的评价指标整理为5个：转让收益、技术应用能力、市场地位、成果适应性、市场开发和营销能力。由此，科技成果供给主体对于需求方的评价指标集为U={u1，u2，u3，u4，u5} ，其指标权重向量通过7个技术供给方所给权重的加权平均而得Wu={0.46，0.23，0.14，0.1，0.07}。如表1所示。

同样，科技成果需求方在进行供给方选择时的关注要素主要集中在科技成果的技术先进性、科技成果的技术易转化性、科技成果的市场潜力[1]。同时参考我国《关于改进科学技术评价工作的决定》等为促进科技评价工作的政策法规，以及考虑对样本企业的问卷调查，本文提取出5个科技成果需求方对供给方的评价指标，分别是：交易价格、市场预期、技术成果创新性、技术成果应用复杂性、技术支持。因此科技成果需求主体对于供给方的评价指标集为V={v1，v2，v3，v4，v5} ，同样的加权平均得出对应的权重向量为Wv={0.31，0.24，0.19，0.17，0.09}。如表2所示。

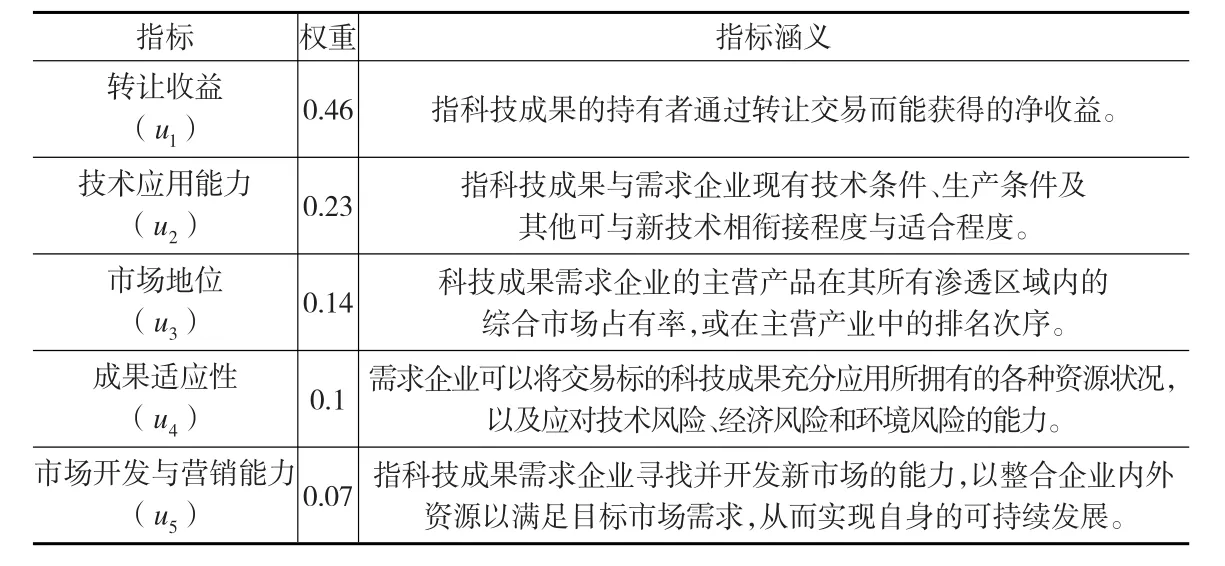
表1 技术成果供给方对需求方评价指标体系

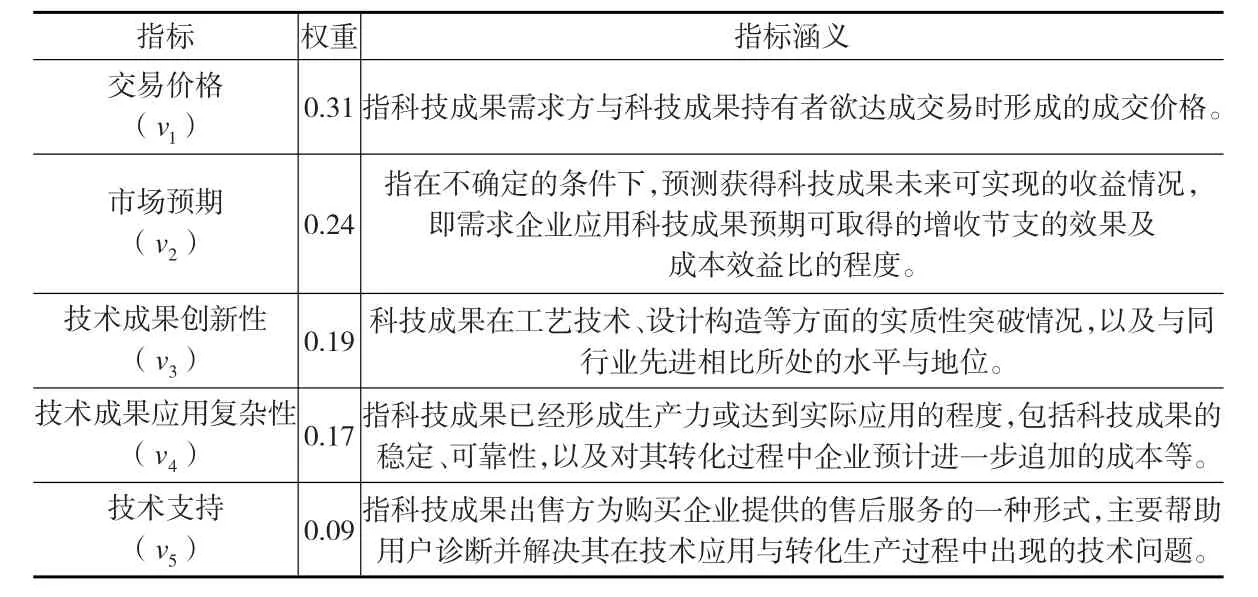
表2 技术成果需求方对供给方评价指标体系

3.2 技术成果供需主体间的满意度评价

依据确立的评价指标体系，科技成果供需双方则可对于彼此间每个主体进行满意度评价，并采用区间直觉模糊数表示。7个科技成果供给方与10个科技成果需求方共产生了140个满意度评价矩阵。以科技成果供给方A1主体对科技成果需求方、科技成果需求方B1对科技成果供给方做出的满意度评价为例，其满意度评价矩阵分别如下：

3.3 科技成果供需主体整体满意度最大化的双边匹配

由满意度矩阵A(B)=(dij)n×m和B(A)=(eij)m×n，进一步得到综合加权满意度矩阵其中wAi和wBj分别表示科技成果供给方Ai与需求方Bj各自的主体权重，考虑到科技服务平台作为中介对于科技成果供需匹配决策的公平性与公正性，因此每个主体取相等权重，即wAi=1/7；wBj=1/10

接着将Z(A)和Z(B)代入，并应用软件LINGO11.0求解，可得到该问题的最优匹配结果为：x15=1，x26=1，x38=1，x47=1，x52=1，x64=1，x79=1；其余xij均为0。因此科技服务平台对于该批膜分离技术的供需匹配结果为：供给方A1与需求方B5匹配；供给方A2与需求方B6匹配；供给方A3与需求方B8匹配；供给方A4与需求方B7匹配；供给方A5与需求方B2匹配；供给方A6与需求方B4匹配；供给方A7与需求方B9匹配。

需要说明的是在求解模型M2时，考虑到科技服务平台的公共服务功能定位，其对科技成果的供需双方的满意度应同等重视，因此权重α，β，γ，δ值均取值为0.5；此外考虑科技成果供需主体双方满意度一致性与互补性对的同等地位，此处权重λ=0.5。但是针对具体的匹配决策，有时会侧重某一方的满意度，以及更注重满意度的一致性或互补性，这会导致λ，α，β，γ，δ会有不同取值。此处，将权重取极端值为例，可见其最优匹配结果的变化，如表3所示。

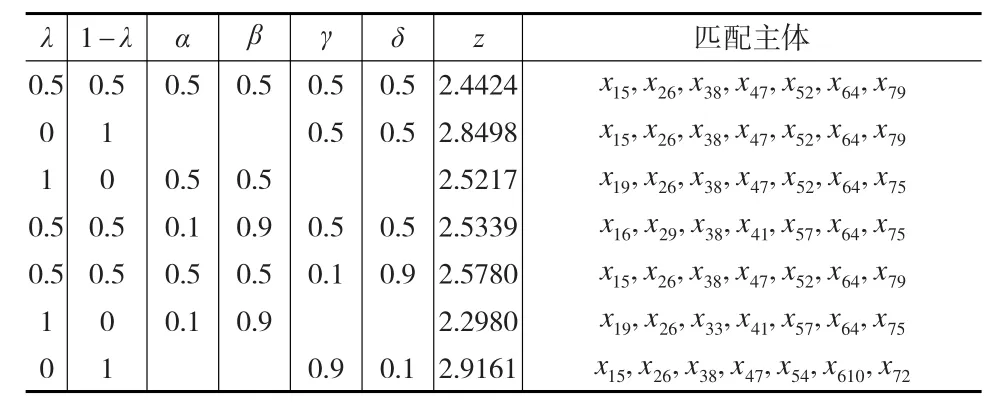
表3 不同权重取值下匹配结果对比

4 结束语

在市场经济条件下，完善科技服务平台运营决策机制是繁荣科技成果市场、提高科技资源配置效率的必备条件。本文基于双边匹配主体满意度的视角，将区间直觉模糊集理论引入满意度评价，提出以整体满意度最大化为目标的优化模型，最终获得最优匹配方案。

构建了科技成果供需匹配优化模型。在原有双边匹配方法的基础上,引入科技服务平台作为科技成果供需匹配中介，改进的科技成果供需双边匹配模型最终以整体满意度最大化为目标，有利于发挥科技服务平台作为科技资源的配置中介的重要作用。

将区间直觉模糊数引入匹配双方主体的初步互相评价结果。通过给出函数加权满意度的定义，将初步评价结果进行集成，同时考虑评价主体的权重，从而得到主体加权满意度。使得决策模型更加真实的反映了科技成果供需双方进行选择决策时存在主观判断、个体偏好及非信息对称的客观现实，提升了双边匹配模型实用性。此外，最终目标函数同时考虑其互补性和一致性，并引入调节参数，使得模型进一步优化，从而使得该模型在面对不同匹配决策需求时具有更强的灵活性。

参考文献：

[1] 何桢,韩俊德,徐炎.企业视角下的天津科技成果转化障碍因素研究[J].北京理工大学学报：社会科学版,2011,13(1).

[2] 汪良兵,洪进,赵定涛.中国技术转移体系的演化状态及协同机制研究[J].科研管理,2014,35(5).

[3] Roth A E.Common and Conflicting Interests in Two-sided Matching Markets[J].European Economic Review,1985,27(1).

[4] 王塑,李西平,王新等.基于双边匹配理论的人员岗位适配性研究[J].人力资源管理,2013,(12).

[5] 贾璐,樊治平,沈凯,徐宝福.知识服务中的供需双边匹配模型[J].东北大学学报：自然科学版,2011,32(2).

[6] 梁海明,姜艳萍.一种考虑中介交易态度的买卖双边匹配决策方法[J].运筹与管理,2013,22(5).

[7] 万树平,李登峰.具有不同类型信息的风险投资商与投资企业多指标双边匹配决策方法[J].中国管理科学,2014,22(2).

[8] Atanassov K,Gargov G.Interval-valued Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1989,31(3).

[9] Xu Z.A Deviation-based Approach to Intuitionistic Fuzzy Multiple Attribute Group Decision Making[J].Group Decision&Negotiation,2010,19(1).

[10] 徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2).

[11] Wang Z,Kevin W L,Wang W.An Approach to Multiattribute Deci⁃sion Making With Interval-valued Intuitionistic Fuzzy Assessments and Incomplete Weights[J].Information Sciences,2009,179(17).

[12] 林杨,王应明,陈圣群.一种考虑区间直觉模糊集的多属性匹配决策方法[J].信息与控制,2016,45(2).