纯电动汽车制动避撞系统的建模与分析∗

李洪涛，赵 韩，黄 康，刘生强

(合肥工业大学机械工程学院，合肥 230009)

前言

汽车避撞系统作为主动安全的重要研究方向之一，对降低追尾事故发生、提高交通运输的安全性具有现实意义。纯电动汽车的安全辅助驾驶系统必将成为研究的新热点。汽车主动避撞系统是利用雷达或者传感器技术识别车辆行驶状态，并根据安全车距模型对车辆的安全状态做出判断，给驾驶员提供预警功能。

国内外学者对避撞系统进行了大量的研究。文献[1]和文献[2]中基于线性二次最优控制理论设计了上位控制系统，基于前馈和PI反馈设计了下位控制器，并通过实验验证车辆纵向控制系统可满足汽车车速控制和车间距控制；文献[3]中基于驾驶员驾驶行为设计了车辆下位控制器，基于混淆矩阵方法优化系统的控制参数，提出了一种新的控制策略，保证车辆运动特性尽可能接近驾驶员实际操作特性；文献[4]中为解决传统纵向控制的模型误差和逻辑判断误差，采用了基于终端滑模控制的分层结构来设计避撞系统控制器，实现安全距离误差和两车相对速度调控最小化的控制目标；文献[5]中将车辆纵向运动状态分为多种模式，在传统纵向避撞系统的基础上增加模式切换层，提出了一种多模式纵向避撞系统控制策略；文献[6]中基于滑模控制方法得到后车制动的期望加速度，考虑驾驶员行驶舒适性，利用车辆通信技术分配前后车辆加速度，完成车辆的协同避撞。

上述针对汽车主动安全避撞系统的研究主要是以传统内燃机汽车为研究对象，并且未考虑模型非线性、系统参数非确定性以及外部干扰的影响。为提高纯电动汽车避撞系统的精度和稳定性，提出一种基于滑模控制的自适应控制方法，可以自适应地调节滑模系统参数以适应外界环境的变化。通过跟车场景下的仿真实验，验证控制器的避撞控制效果。

1 纯电动汽车参数匹配设计

1.1 电机-变速器一体化设计

以某电动汽车为设计原型，开发出一款适用于纯电动汽车动力传动系统结构：电机-变速器一体化装置，减小了动力总成的轴向尺寸，提高了传动效率。具体结构如图1所示。

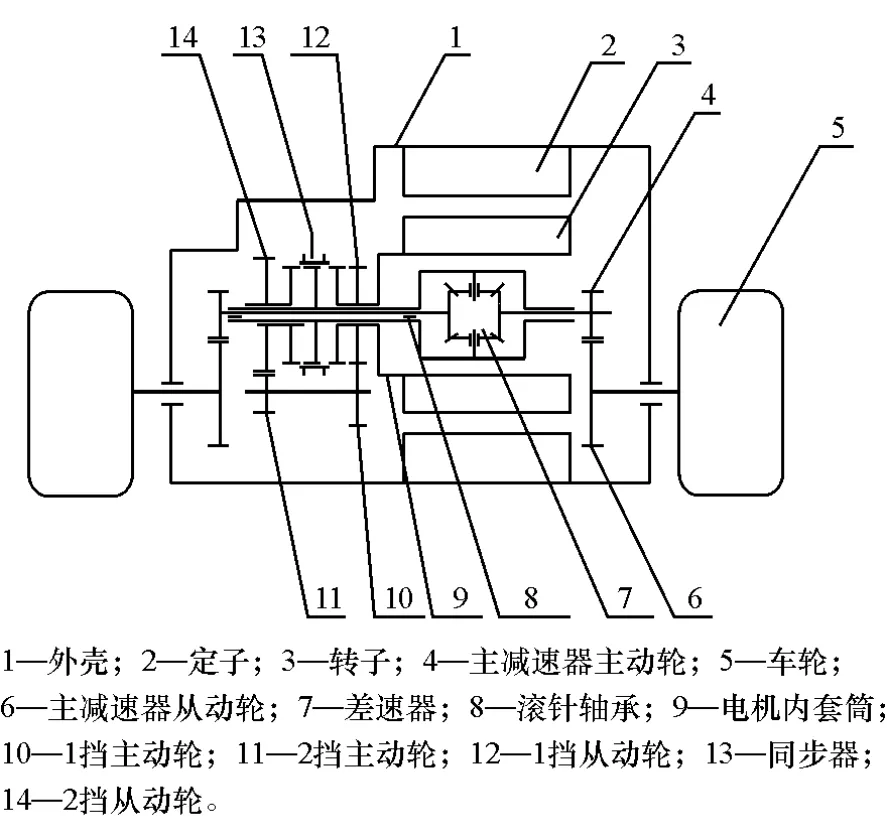
图1 电机-变速器一体化结构示意图

纯电动汽车采用电机-变速器一体化方案时的执行元件工作状态如表1所示。当同步器处于分离状态，此时无论电机处于何种状态，纯电动汽车处于空挡；当同步器与齿轮14接合，动力经 12—10—11—14—差速器7输出到主减速器，电动汽车处于低速挡行驶；当车辆的行驶速度达到换挡条件时，同步器与齿轮12接合，此时动力直接经差速器输出到主减速器，电动汽车处于高速挡行驶；当倒车时，同步器接合情况与低速挡相同，电机反转。

表1 换挡执行元件工作表

纯电动汽车整车的设计参数和主要的动力性能要求如表2所列。

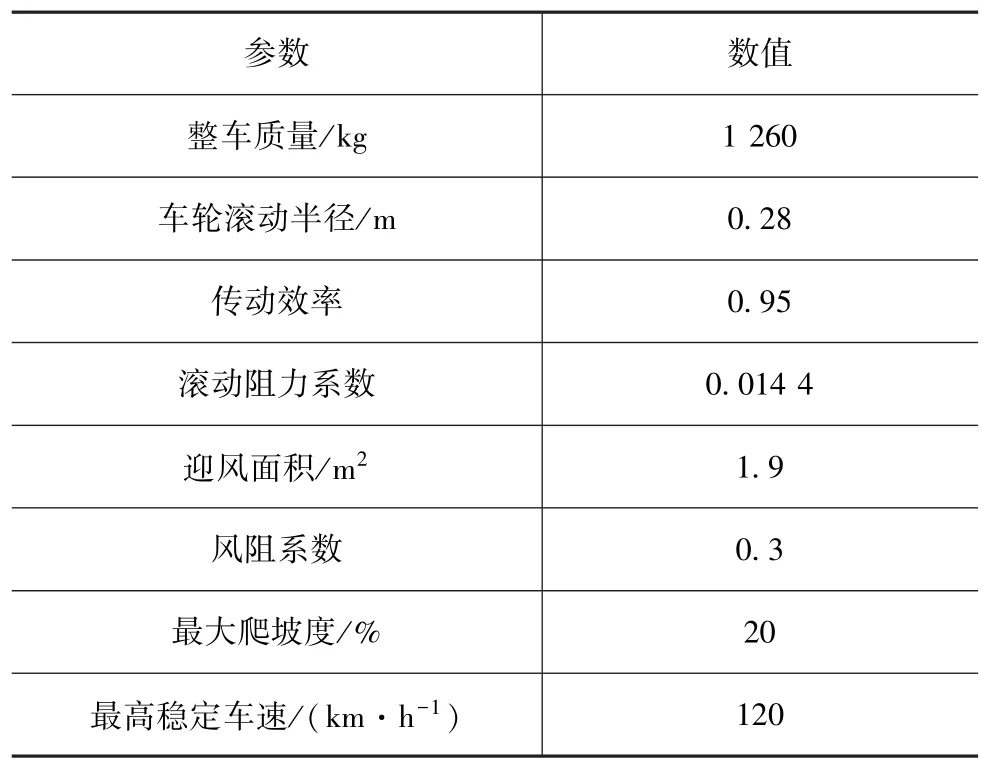
表2 整车设计参数

驱动电机在纯电动汽车低速或者爬坡时输出较大转矩，在高速工况下输出较大的功率。因此，纯电动汽车的动力性需求决定了驱动电机的性能参数匹配情况，即应该满足电动汽车的爬坡性能、最高车速性能和加速性能等指标[7-9]。驱动电机需要确定的主要参数有额定功率、峰值功率、峰值转矩和最高转速。

根据文献[9]中得到纯电动汽车行驶方程为

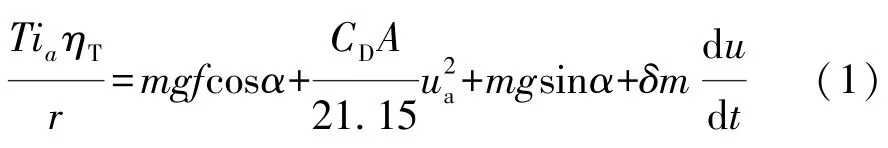
式中：T为电机输出转矩；ia为传动系总传动比，a＝1，2；ηT为传动系统效率；r为车轮滚动半径；m为整车质量；f为滚动阻力系数；α为道路坡度角；A为迎风面积；CD为空气阻力系数；ua为汽车行驶车速；δ为旋转质量换算系数。

纯电动汽车选择的驱动电机功率应不小于在平坦良好路面上车辆以最高速度行驶时阻力功率总和，即电动汽车以最高车速行驶消耗的功率Pe为

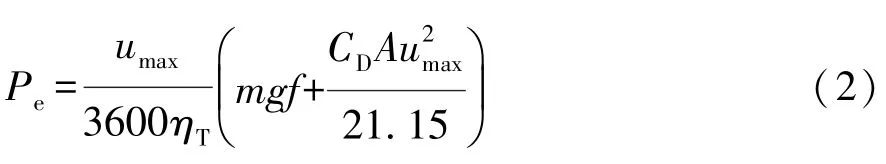
式中umax为最高车速。

电动汽车以某一车速爬上一定坡度消耗的功率Pa为

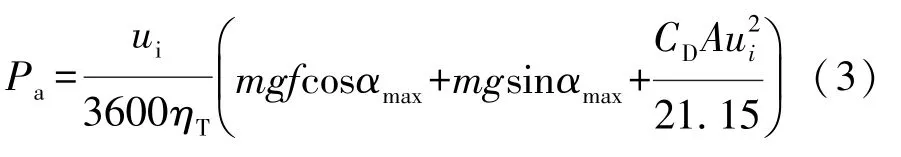
式中αmax为最大爬坡度。

电动汽车在水平路面上加速行驶消耗的功率Pc为

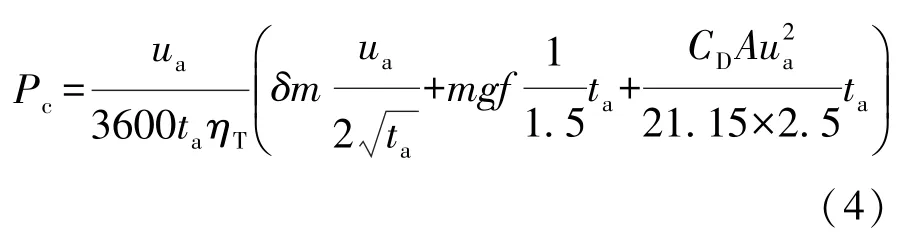
式中：ui为爬坡车速；ua为汽车的加速末速度；ta为汽车加速时间。

电动汽车驱动电机的峰值功率应能同时满足汽车对最高车速、加速时间以及爬坡性能的要求。所以，电动汽车驱动电机的峰值功率为

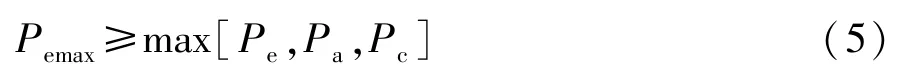
依据计算分析驱动电机所需额定功率与峰值功率，选定驱动电机类型为永磁同步电机，具体参数如表3所示。

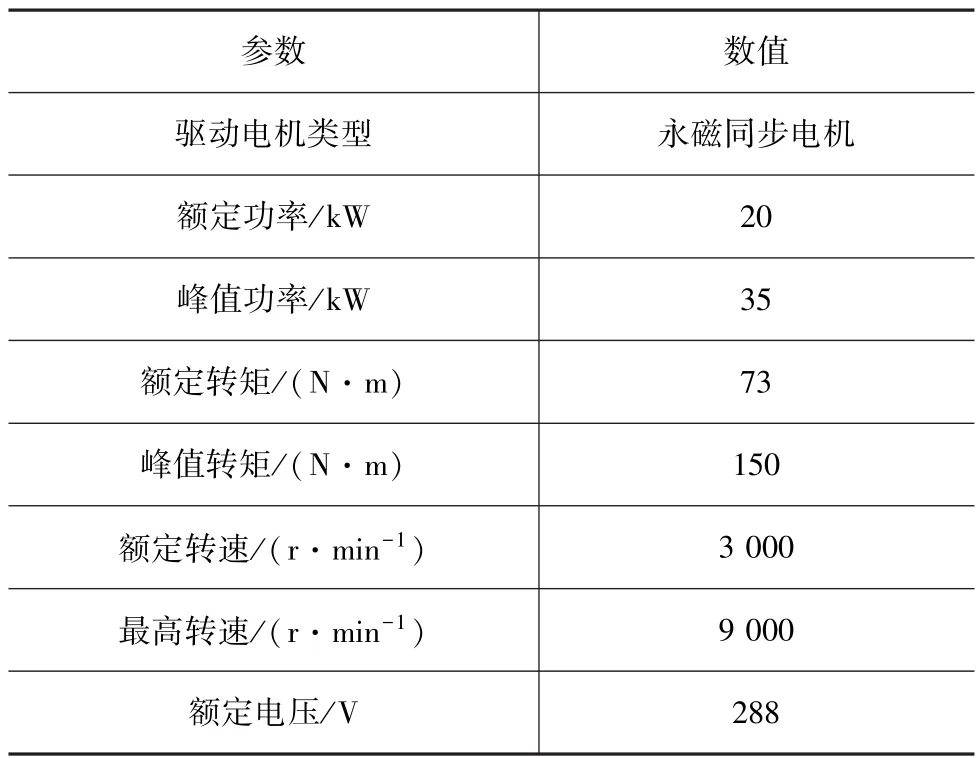
表3 驱动电机参数

1.2 电机-变速器一体化建模

对电机-变速器一体化机构传动系参数选择做计算分析。

1.2.1 传动系速比的上限

变速器传动系速比的上限是由电机最高转速nmax和最高行驶车速umax确定，电机最高转速nmax、最小传动比imin、最高行驶速度umax三者的关系为

其中主减速器传动比ig＝4.5，代入其他参数，可得imin≤7.917，2 挡传动比i2≤1.759。

1.2.2 传动系速比的下限

变速器传动系速比的下限由下述两种情况的传动系速比的最大值确定。

由电机最高转速对应的最大输出转矩和最大行驶车速对应的行驶阻力确定传动系速比的下限为

式中：FVmax为最大行驶车速对应的行驶阻力；TVmax为驱动电机最高转速对应的最大输出转矩。

由驱动电机能输出的最大转矩Tαmax和最大爬坡度对应的行驶阻力Fαmax确定的传动比下限为

代入相关参数，可得最大传动比imax≥8.803，i1≥1.956。

电动汽车在行驶过程中最常用的挡位是2挡，所以在保证动力性能的情况下，应尽量维持电机工作在高效率区间，在满足以上条件情况下，将高速挡设计成直接挡，即传动比为1。同时也间接验证了项目中电机-变速器一体化机构的合理性。另外一方面高速挡挡位数值较大，电机会长时间运行在最高转速区，这对于电机寿命是极为不利的，综合成本和制造工艺方面的考虑，将2挡的数值定为1。而低速挡应该尽量保证车辆的转矩需求，所以结合设计、制造和成本等因素后，将1挡的传动比设计为3。

1.3 执行机构切换逻辑

在驾驶员操纵车辆的过程中，对加速踏板和制动踏板的操作是分开工作的，加速踏板和制动踏板两种操作不能同时完成，否则会造成电机和传动系统的损坏。而且，加速踏板/制动踏板切换逻辑制定应当避免长时间高频率模块切换。

本文中基于上述原则制定切换逻辑来操作节气门位置或制动器。首先，设置电机的节气门初始值为0，求得各速度下的车辆减速度amax；然后，为在操作过程中提高车辆的平稳性，防止操纵模式切换频率太高，模块设置了缓冲区域Δh，根据经验，取Δh＝0.02m/s2。因此，获得的切换逻辑关系为

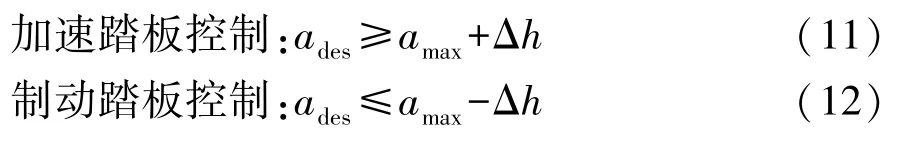
式中ades为车辆期望加速度。

加速踏板/制动踏板切换逻辑模型的输入为获得的期望加速度，输出为求得的车辆制动压力或加速踏板开度。

1.3.1 制动模型

本文中讨论的车辆纵向动力学系统，不考虑车辆旋转部件的质量换算，根据式(1)，车辆制动时运动方程可表示为

式中：ades为期望加速度；Ft为车辆的驱动力；Fxb为路面作用于车辆的制动力；v为汽车速度。

在制动时电机输出转矩为0，即Ft＝0，在不超过路面最大制动力的情况下，制动力Fxb和制动压力pdes可近似表示为线性关系，即

式中Kb为常量系数。

由式(13)和式(14)可得到期望制动压力为

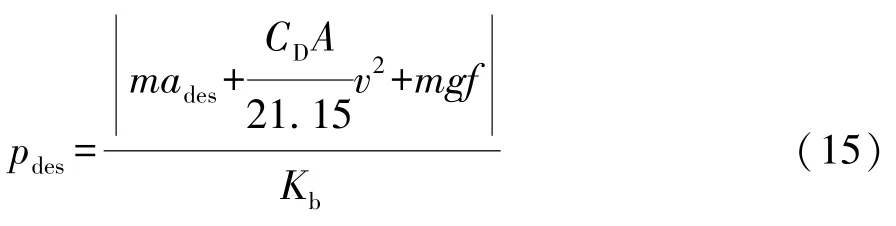
1.3.2 加速模型

若判断为加速踏板控制模块，首先求得期望的电机输出转矩，然后根据所建立的逆电机模块算得加速踏板的开度。

设

则根据式(1)，期望的电机输出转矩可简化为

根据驱动电机转矩特性曲线f(Tdes，we)，即可得到加速踏板的开度αdes为

2 汽车纵向动力学模型

2.1 间距策略设计

在避撞控制系统的行驶过程中，车辆往往处于紧跟状态，所以假定前后车辆速度相等，因此有

式中：Δxdes为期望的安全车间距；th为恒定的车时距；Δx0为最小安全车间距，取决于前车车身长度与车间最小距离。

VTH(可变车头时距)策略采用的车间时距是随汽车行驶状态的变化而做相应改变，这种策略更符合驾驶员实际驾驶习惯。Broqua等人研究表明，行驶过程中的th与自车车速v成线性关系：

式中h1和h2为常量。

当两车的相对速度一定时，若前车突然减速，为保证自车的行驶安全、避免发生追尾，自车应适当减速以增大车头时距；反之，自车可以适当加速在安全前提下减小车头时距，提高系统的效率。所以，在制定间距策略时考虑两车相对速度的变化趋势有利于提高控制系统的动态特性。本文中在原有的VTH策略基础上考虑两车相对速度的变化趋势对期望车间距的影响，设计系统的间距策略。

在车头时距的计算中，引入两车相对加速度代表两车相对速度的变化趋势，可得

式中：vrel为两车相对速度；vp为前车速度；arel为两车相对加速度；t0，cv，ca均为常系数；sat(·)为饱和函数；th-max为车时距上限；th-min为车时距下限。

所以，式(19)和式(20)为考虑两车相对速度变化趋势的可变车头时距策略。该策略不仅考虑了前后车的相对速度，同时考虑了两车相对速度的变化趋势即两车的相对加速度，通过预判前车的速度扰动提高此策略的前瞻性和抗干扰能力，而且利用饱和函数合理设定车时距的取值，使系统更有利于行驶的安全性和跟车效率，适应更加复杂的交通工况。

2.2 间距策略仿真

为验证提出间距策略的准确性，现分别采用CTH(恒定车头时距)策略、原有的VTH策略和改进的VTH策略进行仿真对比。

在仿真试验中，改进的VTH策略中参数取值分别为：th_max＝ 2.2s，th_min＝ 0.2s，t0＝ 1.5s，cv＝ 0.05，ca＝0.3。3种安全距离策略计算出的安全距离如图2所示。

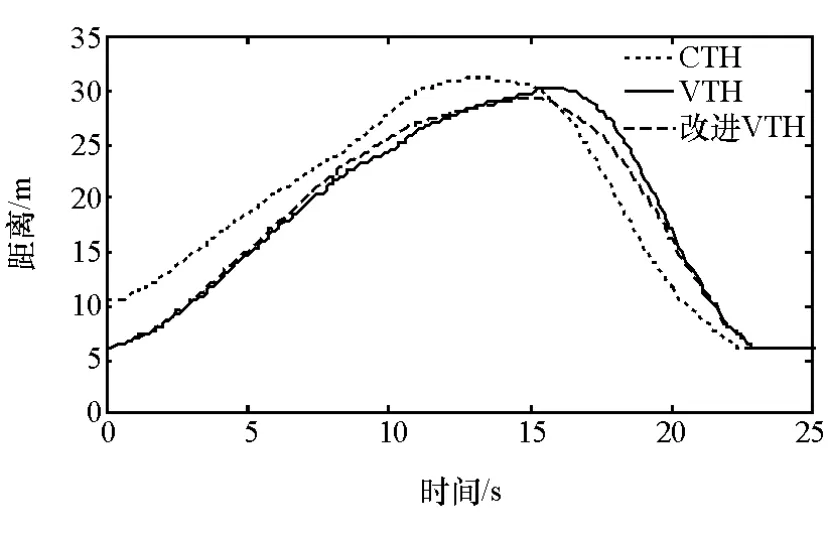
图2 3种安全距离策略仿真曲线

由图2可知，改进VTH算法与CTH算法计算出的安全距离大致相同。但由于改进VTH算法考虑了两车未来速度变化率对安全距离的影响，对应的距离响应曲线相比其他两种策略更为平滑。在跟车情况下，前车的速度频繁发生变化，改进VTH策略都具有很好的适应性：当前车加速时，通过增大期望的车间距来保证自车的行驶安全；当前车减速时，在保证安全性的前提下适当减小期望车间距提高道路的使用率。故这种安全距离算法更加合理，符合实际交通状况[10-11]。

2.3 车辆纵向动力学

避撞系统是以纵向跟车安全性为控制目标，以距离跟踪误差和速度跟踪误差为控制指标，考虑前车加速度对跟车性能的影响，建立基于跟踪误差的纵向动力学模型。在研究避撞系统的动态特性时，首先对模型进行简化，采用如下假设：在汽车跟车行驶过程中，纵向车速远大于横向车速，忽略横向车速对系统的影响，车辆行驶速度等于纵向车速。

车间纵向相对距离、相对速度的控制目标选取改进后的控制策略，即

式中：ed为间距跟踪误差；Δx为实际车间距；ev为速度跟踪误差；ka为速度补偿参数。

对上式微分，可得

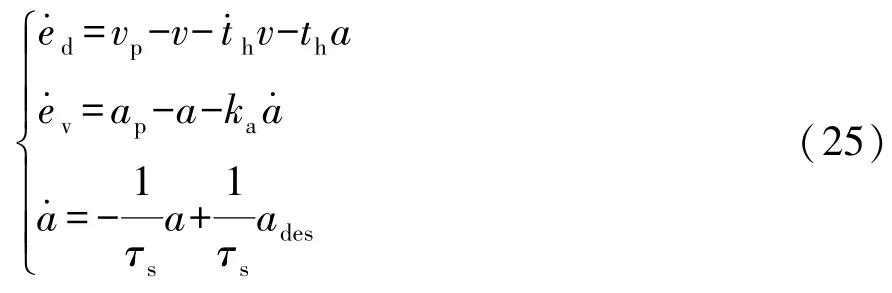
由此可得模型的状态空间方程为

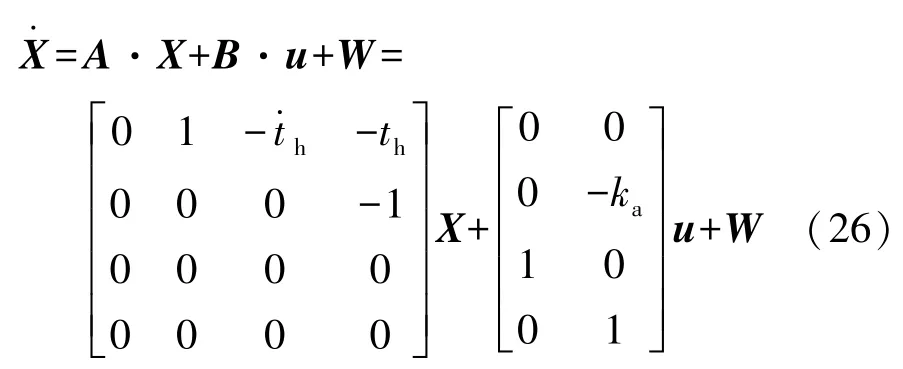
式中：X＝[edevva]T为系统状态矩阵；为控制输入；W为干扰矩阵。

2.4 反馈线性化设计

对汽车避撞系统的数学模型，通过微分几何法的原理，将系统进行反馈线性化设计[12]，求解出：

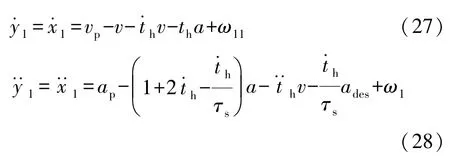
所以，系统的相对阶r1＝2。

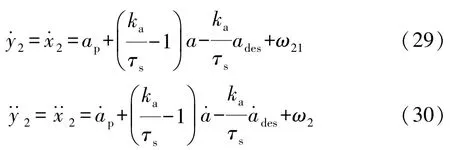
同理可知，系统的相对阶r2＝2。系统的相对阶向量(r1r2)存在，且r1+r2＝n＝4，所以系统状态空间可线性化，且线性化后的系统可控。

根据反馈线性化理论，设

反馈线性化控制律为

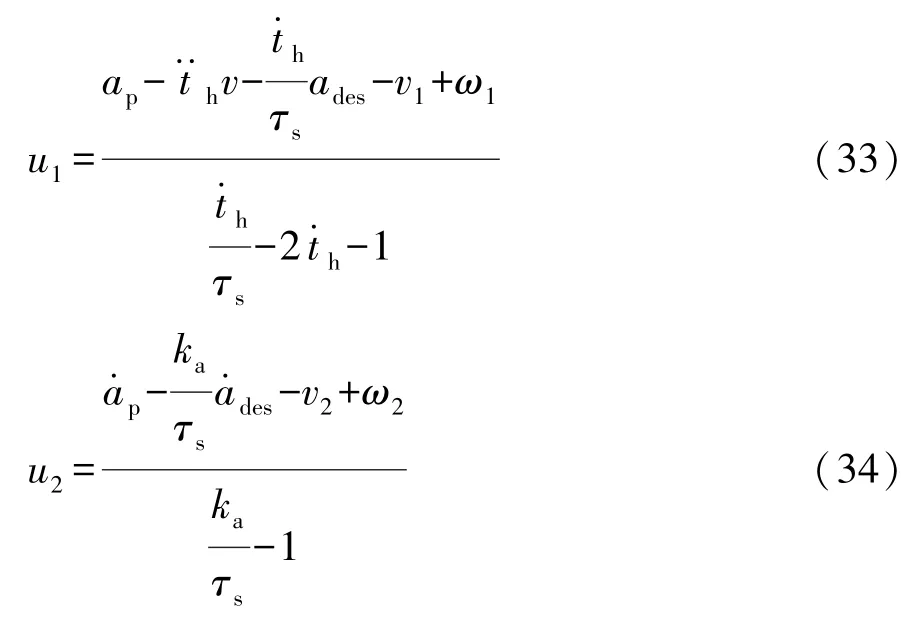
定义系统的控制误差e为期望输出yd与实际系统输出y的差值，设系统的输出期望值分别为x1d，x2d，则

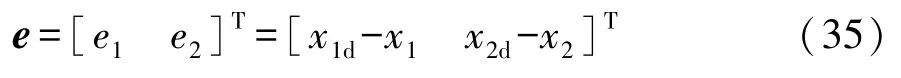
3 控制器的设计

车辆避撞控制系统的性能通过距离跟踪误差和速度跟踪误差来评价。为了得到更好的纵向车辆控制性能，执行的加速度或制动强度不能过大，否则将削弱汽车行驶的横向稳定性和驾驶舒适性。但如果车辆的纵向控制系统性能太弱，会导致追尾或频繁的预警。因此，避撞控制系统性能旨在实现：

(1)系统稳定状态下纵向距离跟踪误差和速度跟踪误差最小(期望值趋向于零)；

(2)距离误差和速度误差应该在驾驶员可控纵向范围内，尽量减小紧急制动对乘车舒适性的影响。

为实现上述目标，根据滑模控制理论，建立控制指标函数：

式中c表示滑模控制器的参数。

对上式求导可得

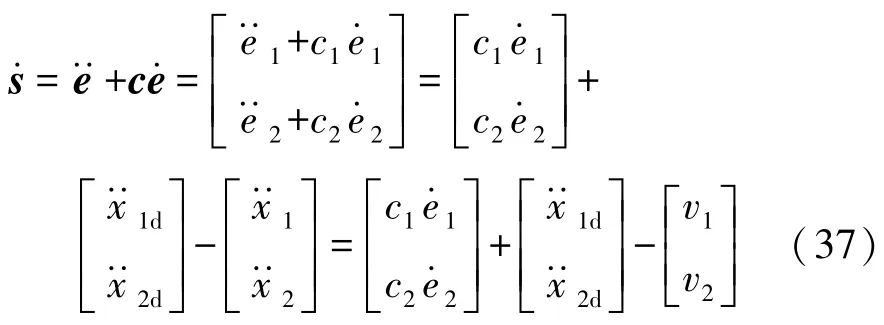
采用指数趋近律的控制方式，控制律为

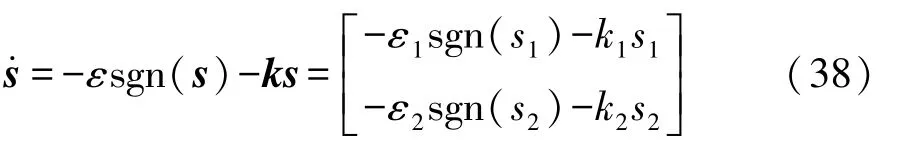
式中：k为指数趋近项常数，该项可以缩短系统的趋近时间；ε为系统的运动点趋近速度，ε小，则趋近速度慢，反之，则运动点达到切换面时具有较大的速度，但会引起较大的抖动。所以，为保证快速趋近的同时削弱抖动，应在选择较大k值同时减小ε。

联立式(37)和式(38)，可求出v1和v2分别为

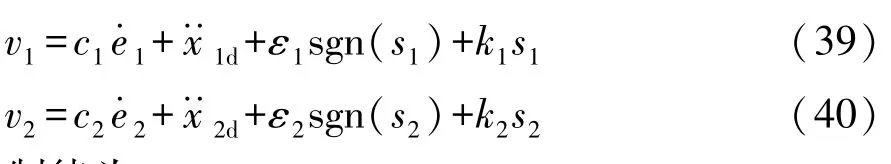
则控制律为

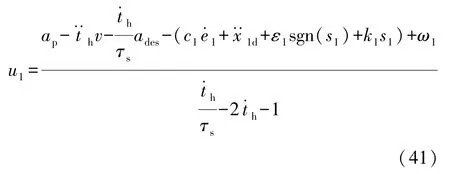
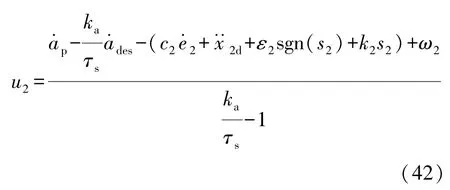
但是，由于W的不确定性，上述控制律无法实际应用。令为不确定项上界的估计值，定义估计误差为

取的自适应律为

式中β为非0设计常数矢量。

为对系统不确定性和外部扰动进行补偿，对上述滑模控制器进行自适应设计，那么原控制器变形为

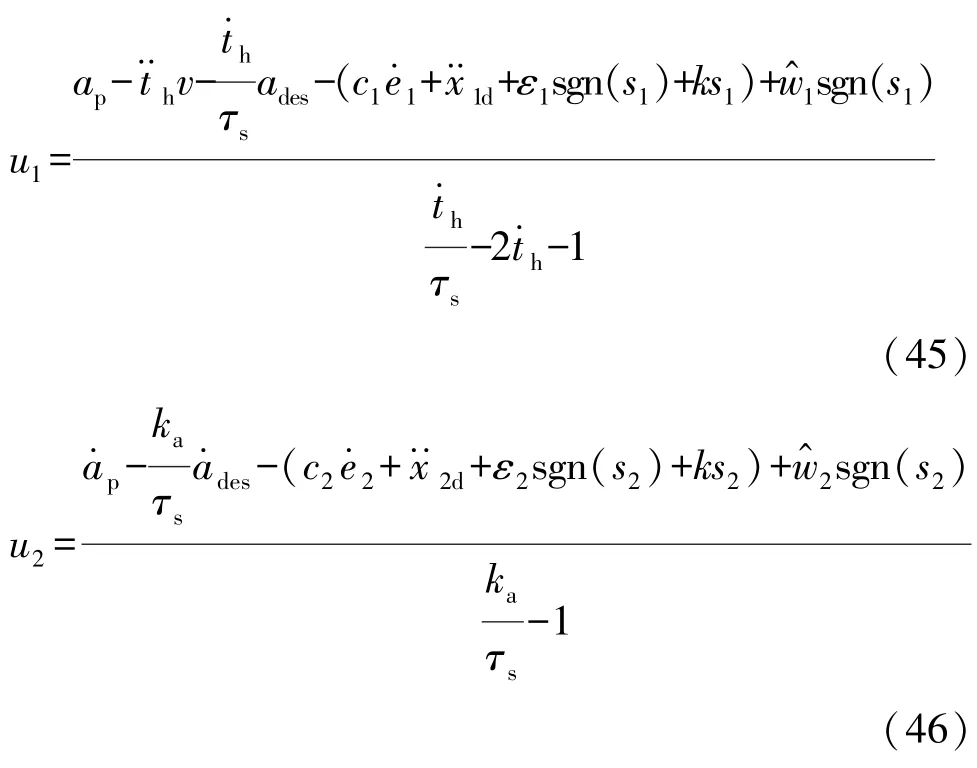
将式(44)带入式(38)中，整理得到

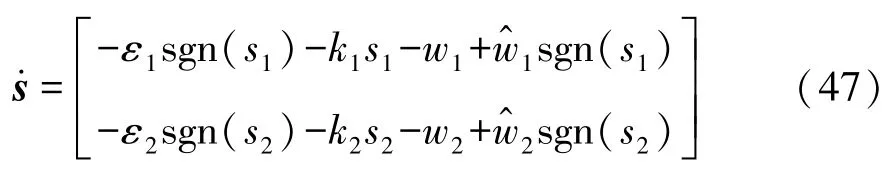
针对上述系统所设计的滑模控制器，进行系统稳定性分析。

取Lyapunov函数为

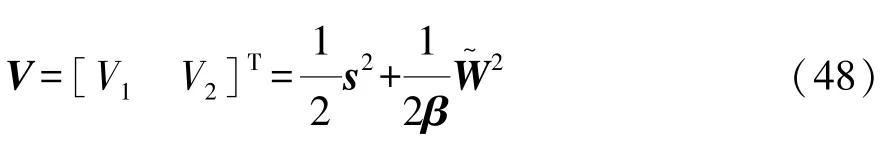
对式(48)求导，得

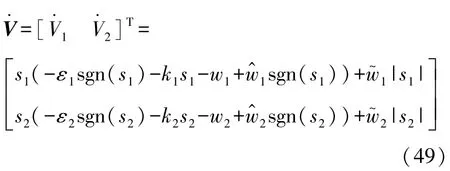
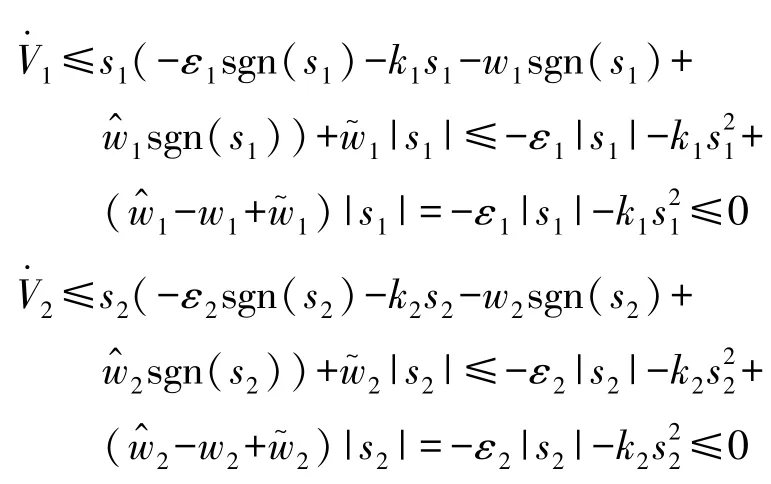
综上所述，系统是稳定的。

4 仿真结果与分析

根据前文的汽车避撞系统纵向动力学模型和控制器，利用Simulink建立避撞过程跟踪控制仿真模型。所设计控制器相关参数分别取为：c1＝10，c2＝15，ε1＝0.1，k1＝10，ε2＝0.15，k2＝15，β1＝10，β2＝5。

主动避撞系统仿真是在当前车道与前车保持安全距离的前提下，装有主动避撞系统的车辆(简称CA车辆)能够根据前车运动状态变化，自行调节速度和距离跟踪控制。为适应复杂的城市交通工况，在低速时对车辆进行有效控制，避撞系统在跟车模式下应具有以下功能：(1)与前车保持安全距离，在前车减速或停车时，能控制本车减速甚至紧急停车；(2)当前车由静止起动时本车能自动起步；(3)当前方没有任何障碍物时，主动避撞系统能控制车速达到期望速度，并保持匀速行驶。

仿真工况初始条件：设定CA车辆和前车初始速度均为0，VTH算法中初始距离dmin取6m，仿真开始时初始车间距为8m，仿真时间80s，在这个过程中前车频繁进行加减速，各控制器参数保持不变。采用所提出的改进VTH间距策略对应车辆的仿真结果如图3～图6所示。

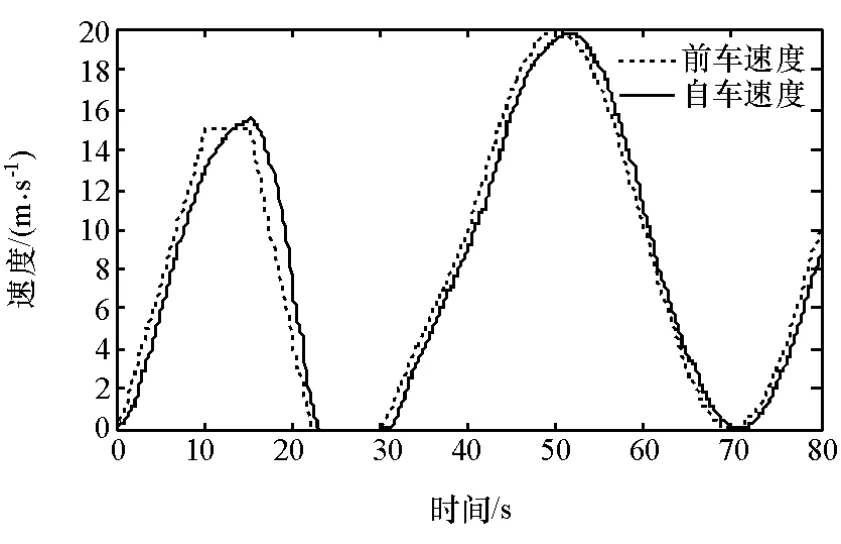
图3 前后车辆速度仿真曲线

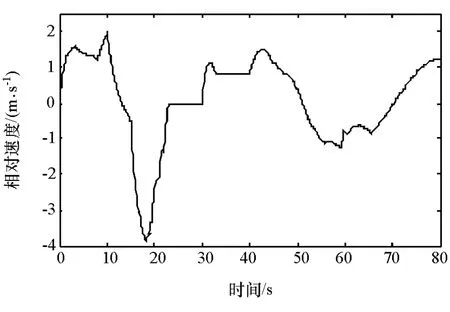
图4 前后车辆相对速度曲线

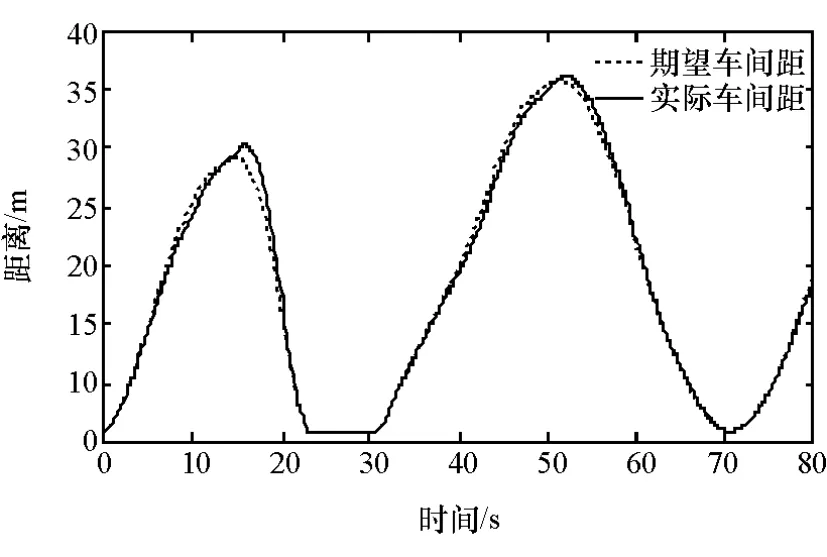
图5 车间距仿真曲线

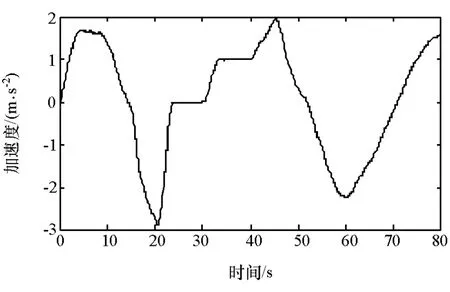
图6 CA车辆加速度曲线

由图3可知，仿真时CA车辆与前车同时起步，速度仿真曲线与前方车辆同步，验证了所开发的CA系统控制策略及算法，能够很好地适应城市交通环境下的跟车行驶工况。由图5可知，CA车辆与前车间的实际距离始终小于或近似等于所开发的VTH距离算法计算出的安全距离，避免与前车发生碰撞事故，提高了行驶安全性，验证了距离滑模控制器良好的控制效果。由图6可知，CA车辆加速度变化很好地反映出汽车运动状态的变化，总体趋势与车速变化相一致。

仿真结果表明，本文研究的控制策略和速度、距离跟踪误差滑模控制器能够很好地应对跟车过程中前车频繁变速的工况，验证了控制策略的正确性和合理性。

5 结论

建立了电机-变速器一体化模型，并提出了一种考虑前车加速度的可变车头时距策略，该间距策略通过引入饱和函数，提高了间距控制的抗干扰能力，可有效地平衡车辆在行驶过程中的跟车性与安全性。

采用控制功能模块、上位控制器和下位控制器联合的纵向分层控制器实现纯电动车主动避撞控制功能设计，并对控制器性能进行了验证。基于滑模控制理论设计的纵向上位控制器体现了驾驶员行驶特性，并对外界干扰和模型不确定性具有一定的鲁棒性。

参考文献

[1]YI K，RYU N，YOON H J，et al.Implementation and vehicle tests of a vehicle stop-and-go cruise control system[J].Proceedings of the Institution of Mechanical Engineers Part D：Journal of Automobile Engineering，2002，216(216)：537-544.

[2]YI K， HONG J， KWON Y D.A vehicle control algorithm for stopand-go cruise control[C].Intelligent Transportation Systems，2001.Proceedings.IEEE Xplore，2001：478-482.

[3]MOON S，YI K.Human driving data-based design of a vehicle adaptive cruise control algorithm[J].Vehicle System Dynamics，2008，46(8)：661-690.

[4]KIM D J，PARK K H，BIEN Z.Hierarchical longitudinal controller for rear-end collision avoidance[J].IEEE Transactions on Industrial Electronics，2007，54(2)：805-817.

[5]裴晓飞，刘昭度，马国成，等.车辆自适应巡航系统的多模式切换控制[J].机械工程学报，2012，48(10)：96-102.

[6]王庞伟，余贵珍，王云鹏，等.基于滑模控制的车车协同主动避撞算法[J].北京航空航天大学学报，2014，40(2)：268-273.

[7]侯德藻，高锋，李克强，等.基于模型匹配方法的汽车主动避撞下位控制系统[J].汽车工程，2003，25(4)：399-402.

[8]徐国凯，赵秀春，苏航.电动汽车的驱动与控制[M].北京：电子工业出版社，2010.

[9]罗莉华.车辆自适应巡航系统的控制策略研究[M].上海：上海交通大学出版社，2013.

[10]刘贵如，周鸣争，王陆林，等.城市工况下最小安全车距控制模型和避撞算法[J].汽车工程，2016，38(10)：1200-1205.

[11]董红召，陈炜烽，郭明飞，等.基于车路一体化的车辆主动避撞系统关键技术的研究[J].汽车工程，2010，32(11)：984-988.

[12]赵韩，邱明明，黄康.基于微分几何的离合器接合过程速度跟踪滑模控制[J].中国机械工程，2015，26(17)：2302-2307.