气 液 两 相 流 压 降 倍 率 实 验 研 究

王微微， 张明柱

(中国石油大学(华东) 信息与控制工程学院，山东 青岛 266580)

0 引 言

两相流系统是相际传质和反应过程中所涉及的最普遍的流动系统，在发动机、航空航天、血液循环、环境工程等领域广泛存在[1-2]。在工程中，流体含气将影响仪表、管道以及阀门设计，严重情况下影响系统的响应速度、控制误差和稳定性等。因此，气液两相流动规律的描述有助于提高系统的性能和可靠性。但是，描述两相流的通用微分方程组至今尚未建立，对两相流规律的深入了解有赖于实验技术的进步[3-4]。

在气液两相流动过程中，由于流动参数(压力、流量、热流密度等)的不同，气液界面的形态及气液在管道中的分布特征会出现较大差别，形成不同的流型[5-6]。流型对气液两相流的参数估计影响较大[7]。目前，气液两相流的测量模型多是基于单相流理论研究基础获得。Murdock[8]引入了Lockhart-Martinelli(L-M)参数对分相流进行修正；James[9]在均相流模型的基础上修正了气液两相的混合密度；林宗虎[10]在Murdock修正模型的基础上考虑气液两相密度比和两相滑速比来进一步提高模型的估计精度；申国强等[11]基于林宗虎模型，根据差压信号的平均值和相对方差测量两相流的流量和质量含气率；Xu等[12]建立了两相流质量含气率与差压信号相对方差的关系式，结合林宗虎修正模型，估计分相流量和质量含气率。

L-M参数反映了水平管中气液两相流动压降与空隙率关系[13-14]；弗劳德数Fr能够反映气液相的折算速度、压力、密度等诸多因素间的内在联系[8,15]。本文设计了实验装置，研究了流型、L-M参数以及Fr对两相压降倍率的影响，根据实验测试参数修正两相流压降相关式，用于气液两相流参数的估计。

1 实验装置

气液两相流实验装置如图1所示。在本实验中，实验介质为空气和水，分别由空压机和离心式水泵提供。

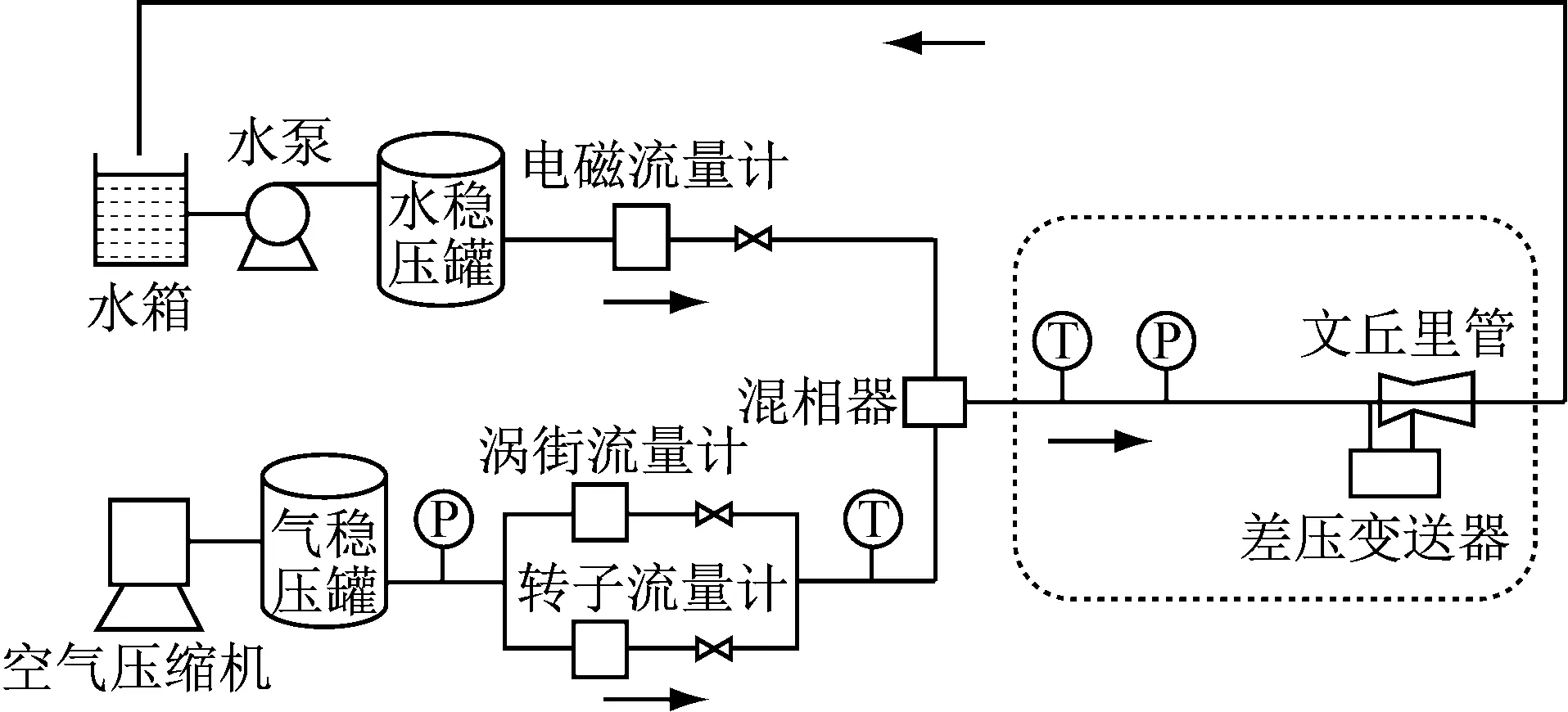
图1 实验装置示意图

空气和水在进入实验管路前通过稳压罐稳压以减小流体的脉动干扰。气体与液体稳压罐的压力分别由空压机和回流阀来调节。稳压罐的压力控制在0.4 MPa。

应用标准仪表测量稳压后的气体与水的参考流量。在气相管路上，应用15和25 mm口径的涡街流量计来计量单相气体参考流量，涡街流量计精度为1级；气相管路上的压力变送器和一体型温度变送器用来计算气体体积标准值。一体型电磁流量计用来测量单相水参考流量，电磁流量计的精度为1级。

气相与液相管道呈45°角伸入混相器，混相器内部管道上的小圆孔使气相与液相充分混合。混相器后长约4 m的直管段保证流型得到充分发展，流型发展段后端0.5 m的有机玻璃管用于观察流型。实验段长约2.5 m，用于安装不同的实验仪表。实验中，文丘里管水平安装于此处。差压变送器测量文丘里管上部和底部的压降。

实验目的是根据文丘里管上部和底部的压降计算压降倍率。实验过程中，保持液相流量稳定，通过调节气相流量来改变含气率，从而改变L-M参数和Fr，通过实验研究L-M参数和Fr与文丘里管压降倍率间的关联关系，建立压降倍率实验相关式。

2 实验参数

2.1 两相流压降倍率

流体流经节流元件时会产生压降。在数值上，两相流与单相流产生的压降不同，两者比值的平方根为两相流压降倍率[16]。气相、液相节流压降倍率定义如下：

(1)

(2)

式中：Δp表示流体流过文丘里管时产生的压降；下标G, L, TP分别表示气相、液相和两相混合流体。

2.2 L-M参数

L-M参数X定义为液相与气相各自单独流过管道时的压降比值的平方根，可表示为：

(3)

若气液两相流经文丘里管时的节流系数相等，则X可写为：

(4)

2.3 Fr

在单相流体中，Fr是描述惯性力与重力的无量纲数，能够反映气液两相流多个流动参数的内在联系。在两相流测量模型中，考虑两相表观速度，Fr分为气相Frg和液相Frl，分别表征气相与液相诸多因素的关联，定义如下：

(5)

(6)

式中：wsg、wsl分别表示气相与液相折算速度(m/s)；g为重力加速度(m/s2)；D为管道内径(m)。

3 实验结果及分析

3.1 Fr对Φg的影响

本实验着重研究了X、Frg对Φg的影响，不同Frl工况下，Φg与X的关系如图2所示。图中，对于同一Frl，Φg随X的增大而增大，Φg与X成近似线性关系，与Murdock模型中关系类似，所以本实验在Murdock模型的基础上对压降倍率进行修正。对于同一X，Φg随Frl的增大而减小，即在图2中，当Frl从1.338增大到3.939时，所对应直线的斜率减小。由此可见，Φg与X的线性关系的斜率受Frl影响。在Murdock模型中，压降倍率关系式的斜率为常数1.26，本实验中，用Frl对压降倍率关系式的斜率进行修正。

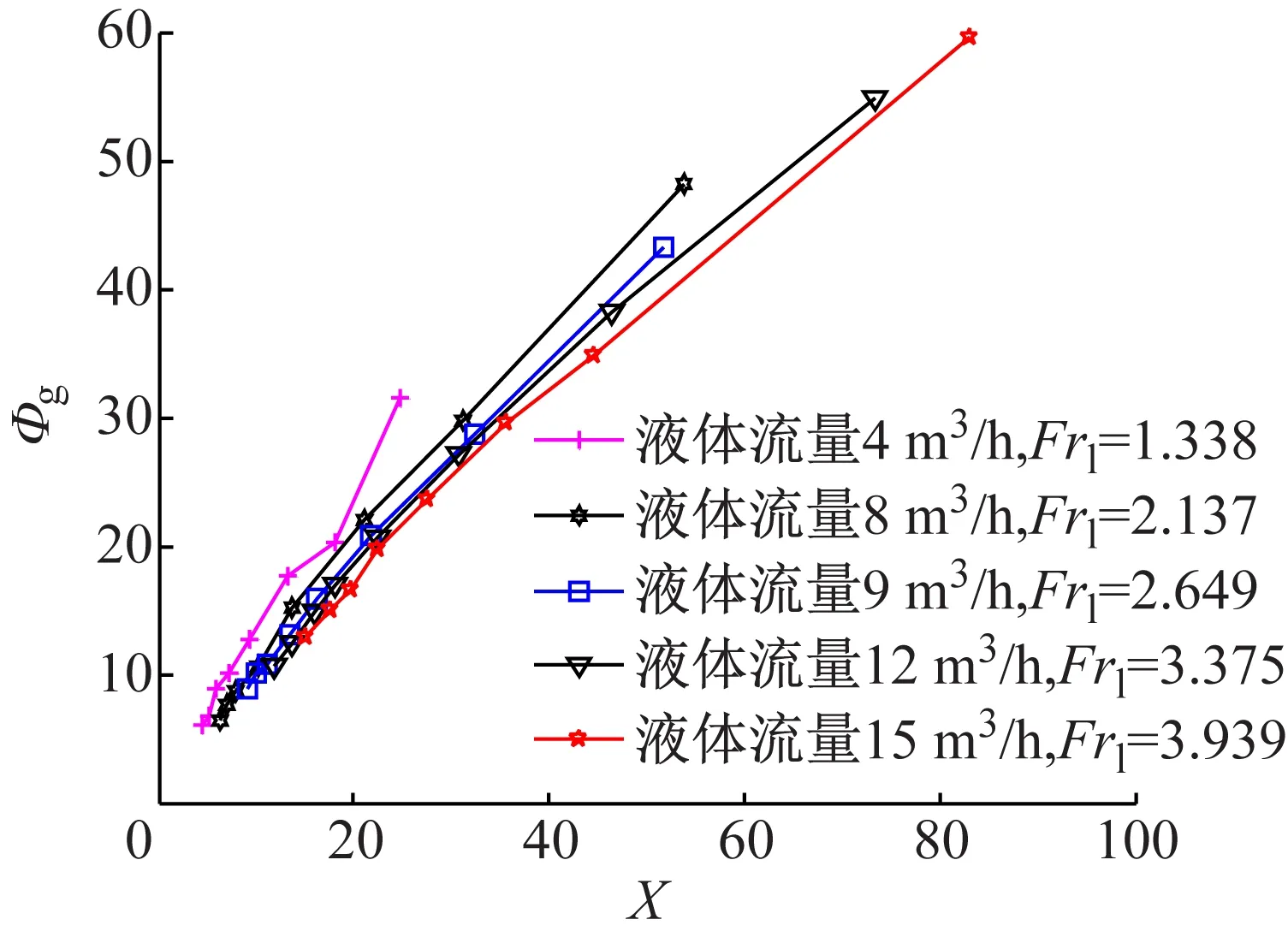
图2 Φg与X的关系

3.2 流型对Φg的影响

不同流型下Φg与X的关系如图3所示。图中，相同流型下，Φg与X的线性关系的斜率相同；而在不同流型下，Φg与X的线性关系的斜率和截距都不同，即流型影响Φg与X线性关系的斜率和截距。本实验针对不同流型来修正压降倍率关系式的斜率和截距。

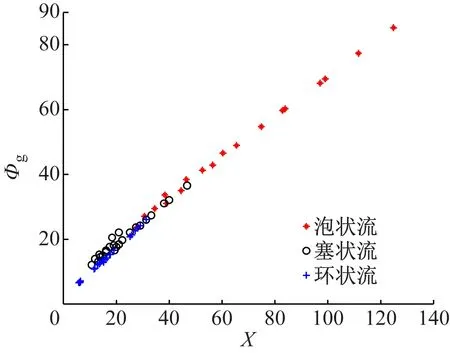
图3 不同流型下Φg与X的关系

综上所述，Φg与X的关系与Murdock模型的关系式有相同的形式。对于文丘里管，流型同时影响Φg与X线性关系的斜率和截距，Frl影响Φg与X线性关系的斜率。因此，本实验基于流型和Fr对Murdock模型进行修正，修正的关系式如下：

(7)

式中：C2为不同流型下Φg与X线性关系的斜率；C1为不同流型下Φg与X线性关系的截距；γ为文丘里管的孔径比。本实验中，不同流型下的C1和C2为：

泡状流C1=10.720 7；C2=0.15。

塞状流C1=6.191 8；C2=0.18。

环状流C1=2.364 7；C2=0.21。

3.3 实验结果与分析

本实验对均相流模型、分相流模型、James模型、Murdock模型、Chisholm模型、林宗虎模型和新建立的模型进行了对比分析。为比较各个模型在估计Φg时的精度，采用下列几种误差指标进行衡量：

相对误差

平均相对误差

均方根误差

比例数

P5=(N5/N)×100%

P10=(N10/N)×100%

P20=(N20/N)×100%

式中：i为第i个实验点；Φgci和Φgi分别为Φg的实验测试值和参考值；N为实验点总数；N5为|Eri|<5%的实验点数；N10为|Eri|<10%的实验点数；N20为|Eri|<20%的实验点数。

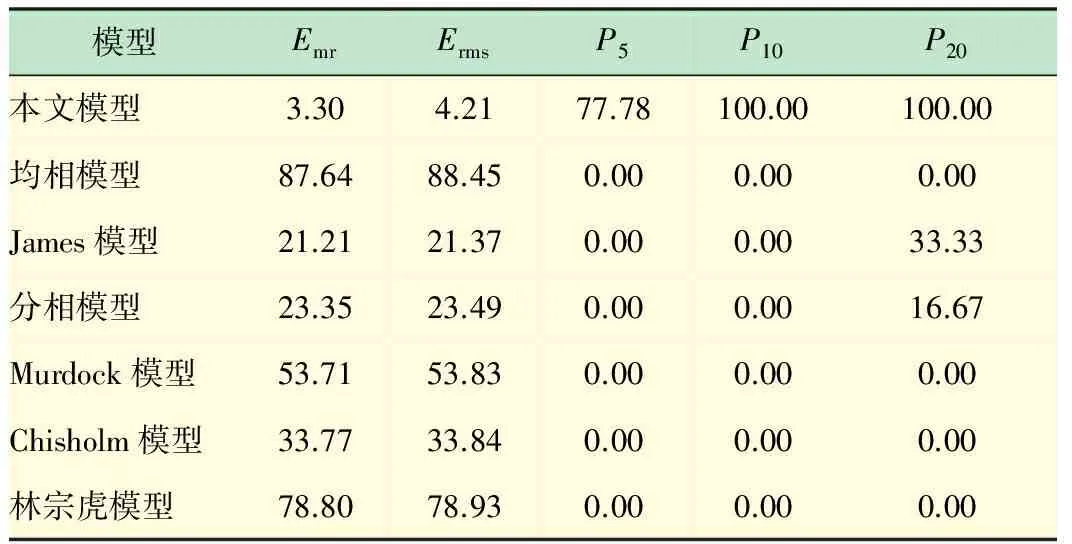
如图4和表1所示，对于泡状流，不同模型下实验测得的Φg相对误差都出现了一定的波动。新建立的模型实验测得的Φg总体波动较小，相对误差比较平均，其中Emr< 4%，Erms< 5%。从比例数P20来看，泡状流工况下，气相压降倍率Φg的实验误差均小于20%。

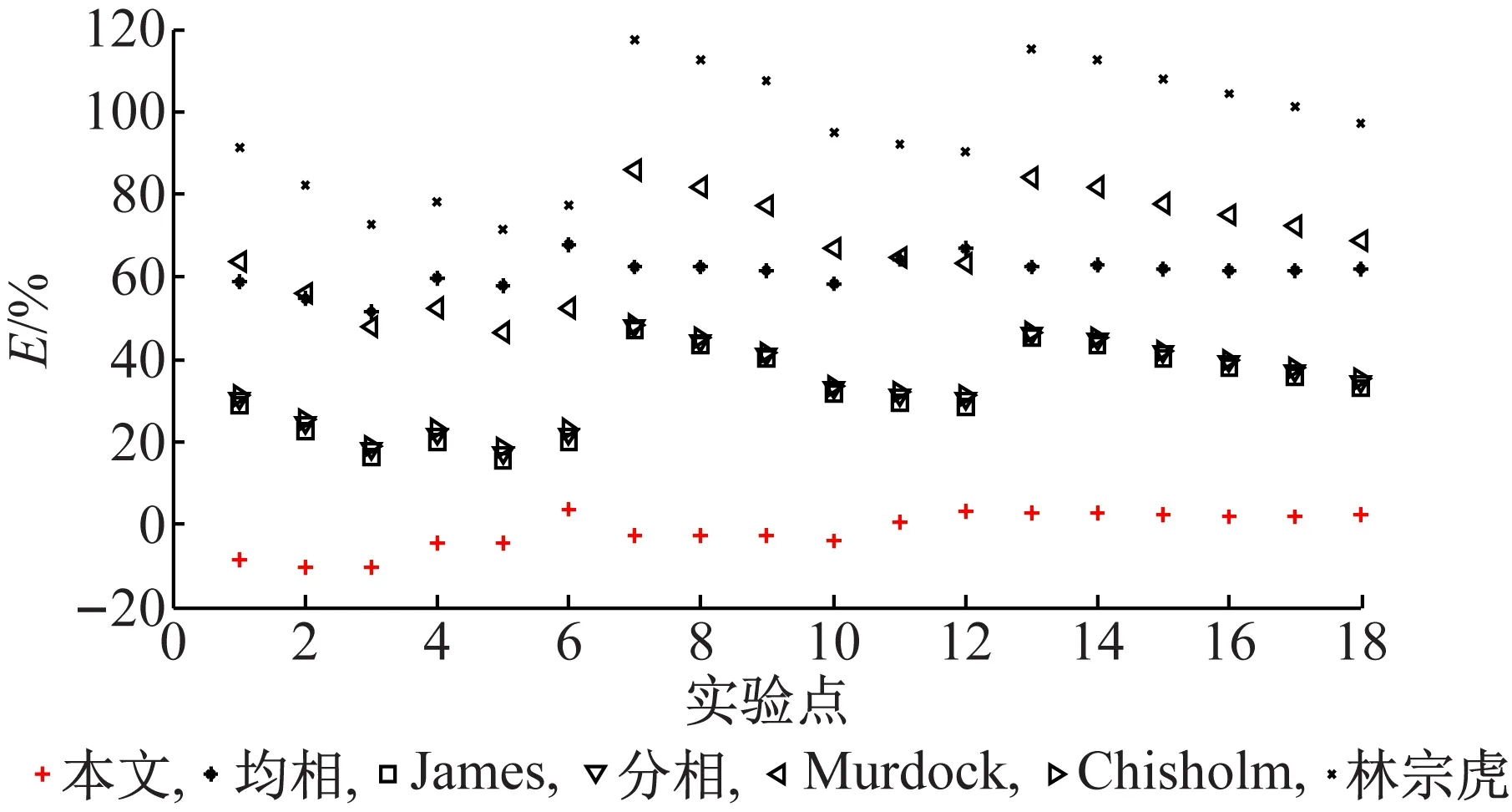
图4 泡状流下Φg实验结果

在泡状流实验工况下，气相主要以分离的小气泡状态散布在连续的液相中。大量小气泡在水平管中分布较均匀，这使得两相压降波动不大，压降相关式精度较高。但是，大量的小气泡运动轨迹复杂，小气泡与流体间存在一定的相互作用，这种小气泡运动引起的频繁扰动导致压降实验结果仍有待提高。

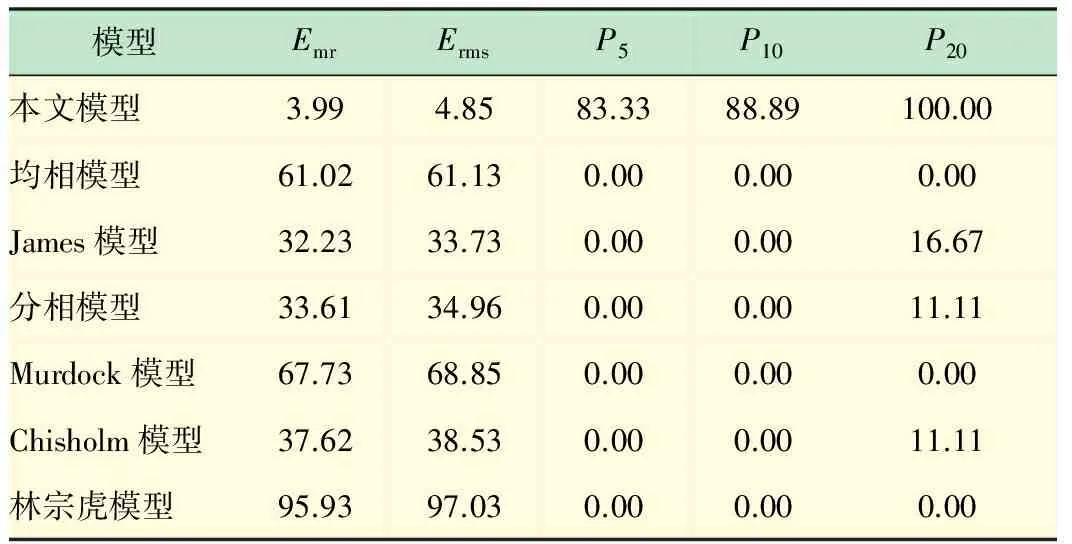
表1 泡状流下Φg误差分布 %

如图5和表2所示，对于塞状流，不同模型的相对误差也出现了一定的波动，且波动幅度较泡状流大。但若将新建立的模型与其他模型对比，相对误差波动仍较小，其中Emr<6%，Erms<7%。从比例数P20来看，塞状流实验工况下，Φg实验误差均小于20%，但P5较泡状流有所减小。

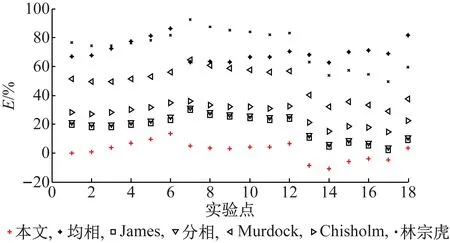
图5 塞状流下Φg实验结果表2 塞状流下Φg误差分布 %

在塞状流流型下，含气率较高，流体流动速度较低，部分小气泡合并成较大的气塞散布在液相中，液相仍为连续项。在大的气塞之间还分布较多小气泡。这种大气塞、小气泡与连续液相并存的流动状态比较复杂，相分布不均匀，相界面复杂多变，相间作用力时大时小，这都导致两相压降波动剧烈。与泡状流和环状流相比，压降相关式的准确性不高。

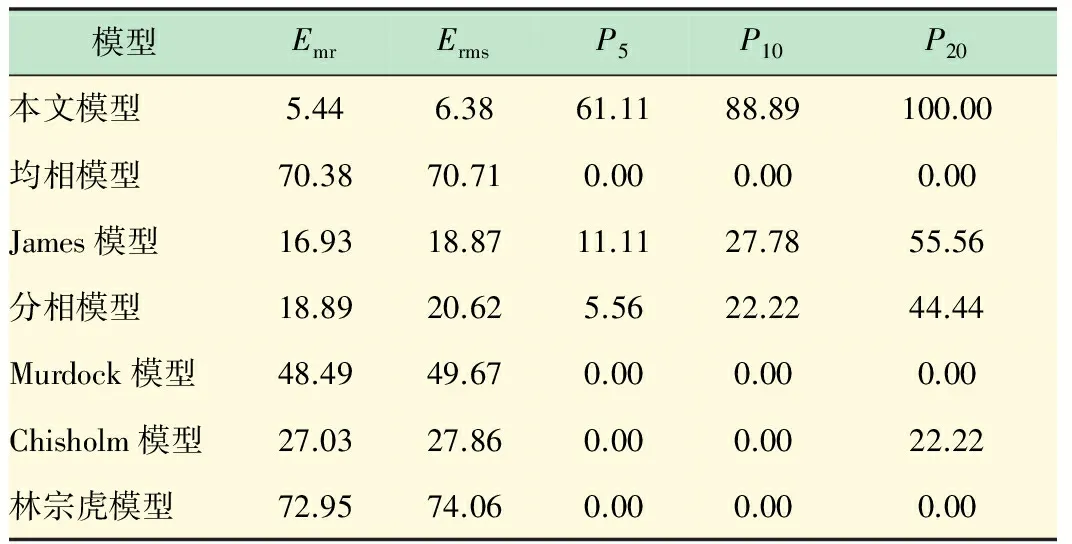
如图6和表3所示，对于环状流，只有均相流模型的相对误差出现了较大的波动，其他模型波动都很小，即相对其他两种流型来说，环状流的相对误差分布最为平均。由表3可以看到，新建立的模型的估计精度仍较高，其中Emr<4%，Erms<5%。从P10来看，环状流Φg实验误差均小于10%，但P5较泡状流小。

图6 环状流下Φg实验结果表3 环状流下Φg误差分布 %

在环状流实验工况下，两相流的含气率较高，流动速度也较快。较低的液相含率导致液体形成液膜沿管壁流动，气相则形成气芯沿水平管中部流动。此时，相分布较均匀，而且几乎没有气泡的扰动，建立的压降相关式精度最高，实验结果也最好。

4 结 语

实验研究表明，气相压降倍率受流型影响。实验应用流型和Fr修正了Murdock模型，其中斜率修正系数随含气率的增大而逐渐增大，截距修正系数随含气率的增大而逐渐减小。

本实验考虑了流型和Fr的影响，建立了较高精度的压降倍率实验相关式。对比泡状流、塞状流、环状流3种流型下的压降倍率相关式，环状流的实验估计精度最高，相对误差小于10%；泡状流实验估计精度仅次于环状流。本实验建立的压降倍率相关式误差分布较均匀，平均相对误差均小于5%，均方根误差均小于7%。塞状流是比较复杂的一种流型，其气相压降倍率与L-M参数的线性关系会随着实验工况的变化而发生变化，本实验建立的相关式不够准确，与其他两种流型相比，塞状流工况的实验估计精度较低。

参考文献(References)：

[1] 袁春飞, 仇小杰. 超燃冲压发动机研究现状及控制系统关键技术[J]. 航空发动机, 2016, 42(4): 1-7.

[2] 吴立刚, 安 昊, 刘健行, 等. 吸气式高超声速飞行器控制的最新研究进展[J]. 哈尔滨工业大学学报, 2016, 48(10): 1-16.

[3] 孔海利, 郭宪民, 李添龙, 等. 可调式引射器对两相流引射制冷循环系统性的影响[J]. 低温与超导, 2014, 42(3): 48-52.

[4] 张树文, 张 忻. 气液两相流实验的改进[J]. 实验室研究与探索, 2000(6): 43-45.

[5] 王微微, 陈静静, 孙峰超. 基于科氏质量流量计的两相流计量方法研究[J]. 测井技术, 2016, 40(2): 167-170.

[6] Jagan V, Satheesh A. Experimental studies on two phase flow patterns of air-water mixture in a pipe with different orientations [J]. Flow Measurement and Instrumentation, 2016, 52: 170-179.

[7] Roman A J, Kreitzer P J, Ervin J S,etal. Flow pattern identification of horizontal two-phase refrigerant flow using neural networks [J]. International Communications in Heat and Mass Transfer, 2016, 71: 254-264.

[8] Murdock J W. Two-phase flow measurement with orifice [J]. Journal of Basic Engineering, 1962, 84(4): 419-433.

[9] James R. Metering steam-water two-phase by sharp-edged orifices[J]. Proceeding of the Institution of Mechanical Engineers, 1956, 180(23): 549-566.

[10] Lin Z H. Two-phase flow measurements with sharp-edged orifice [J]. International Journal of Multiphase Flow, 1992, 8(6): 683-693.

[11] 申国强, 林宗虎. 应用动态法进行气液两相流的双参数测量 [J]. 计量学报, 1993, 14(2): 140-145.

[12] Xu L J, Xu J, Dong F,etal. On fluctuation of the dynamic differential pressure signal of Venturi meter for wet gas metering [J]. Flow Measurement and Instrumentation, 2003, 14(4-5): 211-217.

[13] Konishi C A, Qu W L. Toward a generalized correlation for liquid-vapor two-phase frictional pressure drop across staggered micro-pin-fin arrays [J]. International Communications in Heat and Mass Transfer, 2016(75): 253-261.

[14] Li D. Research of characteristics of gas-liquid two-phase pressure drop in microreactor[C]//MATEC Web of Conferences. EDP Sciences, 2015: 25.

[15] Gupta B, Nayak A K, Kandar T K,etal. Investigation of air-water two phase flow through a venture [J]. Experimental Thermal and Fluid Science, 2016(70): 148-154.

[16] Hewitt G F. Measurement of two phase flow parameters [M]. London: Academic Press, 1978: 60-75.