龙卷生成动力学初探

高守亭 左群杰 杨帅

（1中国科学院大气物理研究所云降水物理与强风暴实验室，北京 100029；2中国科学院大学，北京 100049）

0 引言

龙卷是迅速旋转的空气柱，这个空气柱可以接触到地面，也就是说龙卷是柱状的涡旋，会带来大风，甚至暴雨和冰雹，所以通常又称为龙卷风。在干旱或沙漠地区也有龙卷存在，它是以携带沙尘和碎石而被人们观测到的旋转气柱。在海上或湖泊里也会出现水龙卷，可以看到水面以上的空中水柱及漏斗云的存在。

龙卷的生命史很短，大部分生命史是10 min到1h，影响范围从几米到2 km，但龙卷旋转性强，风力大，带有很大的破坏性，常造成大树连根拔起、房屋倒塌、人员伤亡等灾害。

我国龙卷多发生在苏北、河南中东部以及广东佛山、湛江一带（图1），即相对较平坦的地区。同样，在美国多发生在俄克拉荷马及周边地区也是相对平坦的地方。因为在这样比较平坦的地方其下层容易因为热力差异而造成明显的空气辐合及因大气中低层强风切变而造成上升运动产生局地对流，进而发展成龙卷。

图1 广东湛江龙卷[1]Fig. 1 A tornado occurred in Zhanjiang of Guangdong Province

在国外，特别是美国，对龙卷的研究很多，如Agee等[2]，Alexander 等[3]，Bluestein[4-5]，Brown等[6]，Davies-Jones[7-8]在我国对龙卷也做过一些研究，特别是北京大学孟智勇[9]。但目前主要限于观测事实的揭露和结构动力的诊断分析，对其发展的动力学在我国甚至在世界范围内都很少研究。

1 龙卷发展过程中的动力学

龙卷的生成有4个阶段。第一，对流单体的生成与发展；第二，能量的集中与释放；第三，涡旋的形成与变化；第四，涡度的集中与收缩。依据这4个阶段对龙卷的发展有如下动力学看法。

1.1 对流云中强垂直运动的出现

以往对垂直运动的估计有几种不同的方法，主要有连续性方程计算方法，即利用P坐标系中的连续性方程，通过积分而得到垂直运动。这种方法有一定缺陷，因为垂直运动满足了连续性方程但是不一定满足热力方程和动量方程。真正垂直运动的计算还是应从动量方程出发求得。在任何短的瞬间，运动可以看成定常的，即有于是有

即为

其中Bk为浮力。

方程（2）两边同时点乘速度方向上的位移dr，于是有

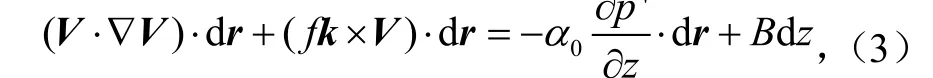
或写为

即

两边积分得

从方程（6）可知

对初始远离积云发展区的运动的空气质点，可认为，则初始时也有B=0。方程（7）可简化为

得到

对在从对流层低层向对流层中层运动的空气质点，有理由认为的值＞的值，因为空气质点在保持动量守恒的过程中，从低层走向高层时，空气的密度明显减小，而迫使质点的速度加大，以满足动量守恒，于是可推测到

其中0＜α＜1。

将方程（10）代入到方程（9）得到

将方程（11）代入到方程（7），并认为是在对流区内，则有

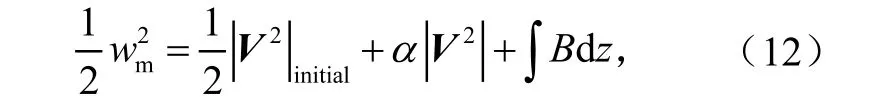
在对流层中层CAPE可表示为

故有

由此可以看出，强对流系统中垂直运动w的值应如式（14）表达，同时也应满足连续性方程。由于对流层中层风速较大，所以wm的值明显取决于对流层中层水平运动的风速Vm。可见，对流层中层大风的出现是强对流发展的信号，也是一种预报指标。再者，由于wm应满足连续性方程，大的垂直运动必造成大气中层及其以下的强辐合，因此中层以下的强辐合区也是一个预报积云发展的重要指标。

1.2 能量的集中与释放

任何系统的发展都需要能量的供给。因此寻找局地能量集中区，也是龙卷发展过程中的重要环节。由于能量集中一般在时间尺度上是短时的，所以不用考虑科氏力的作用，所以有如下运动方程[10]

这里是重力势，单位体积的动能为。

方程（15）两边同时点积V，则有

对短时间天气过程来说，可以看成是绝热的，因此有内能变化为

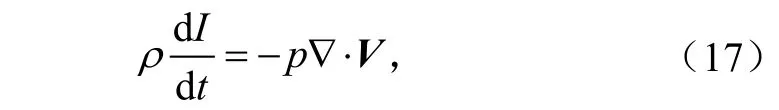
其中，且有

利用式（16）～（18）可以得到

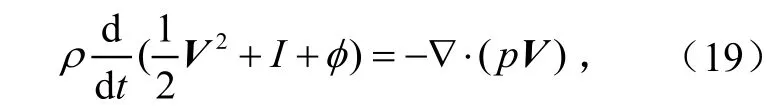
利用质量连续性方程有

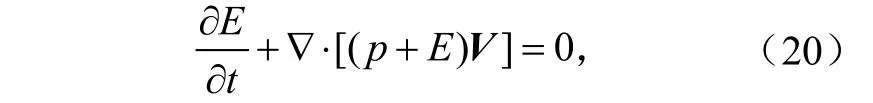
其中：

方程（20）可进一步写为

可见预报最大值的地区是很重要的，由于

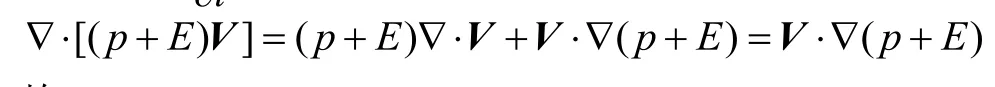
故

可见在能量分析过程中第一步要先寻找能量梯度集中处，然后要看风场对能量梯度的平流。当然最主要的是寻找能量的极值，即的位置。由公式（22）可知必有即能量辐合线上。可见有两边风场对吹，使能量集中而有稳定少动的能量辐合线的存在是很重要的。如果这条辐合线遇到了较大的垂直运动上升区，才会使能量在这条辐合线的垂直运动最大上升区处得以能量释放，使积云系统进一步发展。因此，在天气图上或数值模拟分析图上寻找的辐合线以及的能量极值线是非常重要的。飑线的发生常与这种辐合线与能量极值线的重合有关，也就是在这条线上促进了强对流云的发展。

1.3 涡旋的发展

对龙卷来说，不是通常定义下的用里查逊数Ri来研究其不稳定。如在Ri＜1时会出现对称不稳定，在Ri＜0.25时会出现切边不稳定。因为用里查森数表示的不稳定都是一种波动类型的不稳定，其不稳定可使扰动以波动的形式增长或衰减。可是，龙卷最大的特性是其旋转性，是涡旋的发展及加强。针对这种问题，有两种讨论方法，其一是如果这个龙卷是从地表发展起来的，那它很可能与地表加热或与近地面风切变有关，因为在垂直涡度方程中有

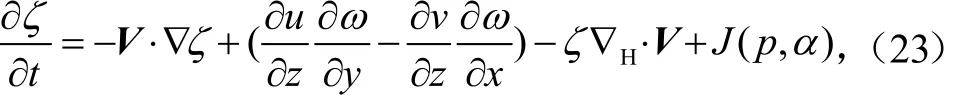
方程（23）右边第二项是水平涡度向垂直涡度的转换项。从这一项中可以看出，如果有明显的水平涡度向垂直涡度转换，则要求要大。在平原地带通常会出现925 hPa上的低空急流，因此在下边界出现了较大的条件，但是在山区因地形不平坦，不易出现925 hPa上的低空急流，所以很难形成的大值，这也是为什么龙卷总是在平坦地区出现而不会出现在山区的原因。另一方面与也有关系。前面讲过高能区或零风速线是产生强对流的源地。在这条零风速线上或高能线上，可得到因只要设x方向沿零风速线即会出现在x方向上垂直运动变化不大，而通常有比较大，这和飑线的产生机制是一致的。飑线前有较明显的入流上升运动而其后有明显的下沉运动，所以南北对比比较大。这里的关键因素还是取决于可见低空急流是促进水平涡度向垂直涡度转换的关键因素。从涡度方程（23）中还可以看出时即水平辐合也是使涡度增长的重要因素。在零风速线上明显存在着水平风的辐合有利于涡度的发展。在这里还有一个关键因素是

在飑线或大的对流单体发生的时候，由于其前的入流及其后的出流会形成气压及温度梯度分布，这样就有利于涡度生成。

另一方面还可以从环流的角度来考察涡度的生成。在Boussinesq近似下，运动方程可写为

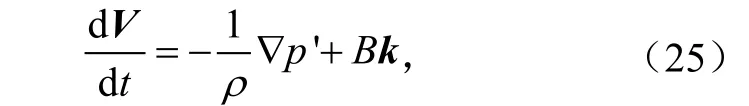
由于所以有得到

由stokes原理得知于是有

由于发生在零风速线上，可以认定因此得到

同时，也有可见浮力Bk的旋度是涡度生成的源。由于地面热源满足与扰动温度成比例，可见地表加热及南北涡度梯度的加大都会造成涡度的加强。

以上是从涡度和环流的方法分析涡度的加强与变化。还要回到最初设定的情况。事实上强旋转的系统都有一个共同的特点，其流动可称为Beltrami 流[8]，即有涡度ω与速度场有如下关系

其中λ是异常量[11]。运动方程可参考文献[8]，如下

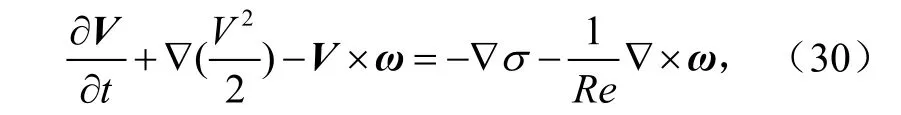
其中是非静力气压梯度力。Re是雷诺数是定常扰动黏性系数。

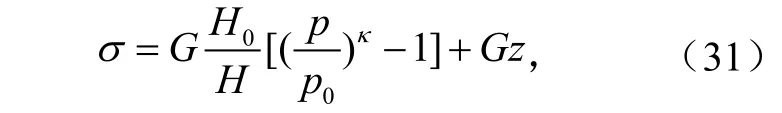
这里，g是重力加速度，p0是地表静压；是绝热大气标高；是无量纲重力加速度；H是研究区域的高度，W0是初始最大垂直速度。

由（29）可知，（30）式为

由于在能量极值线上有于是有

可见，速度的局地变化与雷诺数有关。对于自由大气来说Re很小，可以认为这说明文章开始时假定是相对合理的。

再者，（33）式可写为

可见旋转会引起速度的变化。同时，并利用恒等式便知有的垂直分量为（同时利用连续性方程

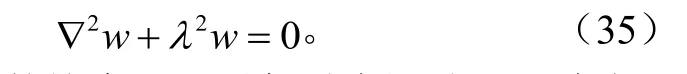
这说明涡度的旋度可以引起垂直运动。因此水平风场与旋转的不均匀都会引起垂直运动。

由以上分析可以看出，龙卷的发生最容易出现在较平坦的地带，因为在平坦地带才容易形成925 hPa上的低空急流，造成大气低层明显的垂直风切变，使空气质点具有较大的水平涡度。再者，大气对流层中层要有较大的风速或者中层急流得以存在，使得对流层中层有较强上升运动出现，这样就会有强对流发展。如果这种强对流是发生在风场辐合线上或在高能极值线上，就会出现像飑线一样的对流系统。如果在辐合线及能量极值线上出现某处的浮力旋度较大，则会产生涡旋。这种涡旋又进一步引起速度的变化及垂直运动的形成，促进旋转区垂直运动的加强，使对流层中低层空气质点由水平运动向垂直运动转化，也使水平涡度转变成垂直涡度，形成极小范围的涡旋柱，即出现龙卷。我国学者薛明等[1]利用自主研发的四维集合卡尔曼滤波方法同化雷达资料首次获得龙卷涡旋内部结构。从高度风场和涡度的回波以及钩状区风场、涡度和气压扰动的垂直剖面中可以看出明显的低层涡旋中心和钩状回波以及深厚的涡旋伴随的强上升运动和负气压扰动。

2 结论

这里从动力学上初步分析了龙卷小概率事件发生的可能条件，但由于问题复杂还需进一步探讨。国际上在该方面也没有成功的探究，也没有固定方法可循。这里只是起了一个抛砖引玉的作用，希望读者对该方面有兴趣共同探究。最后，如果龙卷是从云中掉下来的，甚至不到地面，那还要与水物质相态转换及潜热释放有关，这里不再阐述。

参考文献

[1] Xue M, Zhao K, Wang M, et al. Recent significant tornadoes in China. Advances in Atmospheric Sciences, 2016, 33(11): 1209-1217.

[2] Agee E M, Snow J T, Clare P R. Multiple vortex features in the tornado cyclone and the occurrence of tornado families. Monthly Weather Review, 1976, 104: 552-563.

[3] Alexander C R, Wurman J. The 30 May 1998 Spencer, South Dakota, storm. Part I: the structural evolution and environment of the tornadoes. Monthly Weather Review, 2005, 133: 72-97.

[4] Bluestein H B. A tornadic supercell over elevated, complex terrain: the divide, colorado, storm of 12 July 1996. Monthly Weather Review, 2000, 128(3): 795-809.

[5] Bluestein H B. A review of ground-based, mobile, W-band Doppler-radar observations of tornadoes and dust devils. Dynamics of Atmospheres and Oceans, 2005, 40(3): 163-188.

[6] Brown R A, Wood V T. The tornadic vortex signature: an update. Weather and Forecasting, 2012, 27(2): 525-530.

[7] Davies-Jones R P. Tornadogenesis in supercell storms: What we know and what we don’t know. Extended abstracts, 23rd Conference on Severe Local Storms, November 6-10, St. Louis, MO, American MeteotologicalSociety, Boston,2006. https://ams.confex.com/ams/Annual2006/techprogram/meeting_Annual2006.htm

[8] Davies-Jones P R. Can a descending rain curtain in a supercell instigate tornadogenesisbarotropically? Journal of the Atmospheric Sciences, 2008, 65(8): 2469-2497.

[9] Meng Z, Yao D. Damage survey, radar, and environment analyses on the first-ever documented tornado in Beijing during the heavy rainfall event of 21 July 2012.Weather and Forecasting, 2014, 29(3): 702-724.

[10] Yang S, Zuo Q J, Gao S T. Image of local energy anomaly during a heavy rainfall event. Chinese Physics B, 2017, 26(11): 119201. doi: 10.1088/1674-1056/26/11/119201.

[11] Aris R. Vectors, tensors, and the basic equations of fluid mechanics. Prentice-Hall, 1962: 268.