Winnowing指纹串匹配的重复数据删除算法
2018-05-21王青松
王青松,葛 慧
(辽宁大学 信息学院,沈阳 110036)
0 引言
目前数据激增问题使数据中心处理的数据量呈现爆炸式增长,数据存储、备份和恢复所需的时间和容量也随之增大,给存储系统带来了沉重的负担。由于数据来源不同,许多数据被反复存储,造成了大量的数据冗余,尤其在备份系统中更加突出[1]。重复数据删除技术[2-3]的出现引起了研究者的关注,它不仅能够减少存储和处理的数据量,节约数据的管理和存储成本,同时提高了网络通信的速度,成为降低数据中心冗余数据量的有效手段。
为了在存储系统中充分利用重复数据删除技术,减少数据的最终积累量,缩短消除冗余数据的时间,许多经典的重复数据删除算法被提出。EB(Extreme Binning)算法[4]利用文件相似性,使用最小块签名作为文件的特征,只在内存中保存文件的代表块ID,有效减小了内存占用。然而,最小块ID作为主索引,一方面重删率相对较低,另一方面数据分块算法影响最小块签名,不同的分块算法所产生的最小块可能不同,从而影响重删的准确性。Bloom filter算法[5]利用K个Hash函数将数据块MD5值映射到m位的向量V中,减少频繁的I/O操作,但存在假正例(False Positives)误识别率,并且无法从Bloom Filter集合中删除元素,在需要数据修改的场景下不能使用。张沪寅等[6]提出了用户感知的重复数据删除算法,根据用户相关度,以用户为单位,减少了数据空间局部性,但对于非人为产生的数据,其相似性计算准确度较低。
以上算法在数据分块时均采用了可变长度分块(Content-Defined Chunking, CDC)算法,相对于以文件为粒度,数据块级粒度能够检测到文件内部的重复数据,因此,目前大多数重复数据删除算法均采用数据块为粒度。然而,在现有的许多块级重复数据删除算法中,存在着数据分块效果较差[7]的问题。数据的分块大小很难控制,并且需要预先设置大量的参数,指纹计算和对比的开销较大,分块边界条件也难以满足,而这些问题往往会影响重删操作的性能和准确性。因此,目前大多数数据分块算法都不能使重复数据删除算法达到理想的效果。
本文针对分块算法中以上几点不足,提出了一种Winnowing指纹串匹配的重复数据删除算法(Deduplication algorithm based on Winnowing Fingerprint Matching, DWFM),对基于内容的可变长度分块(CDC)算法进行了改进。实验结果表明,本文算法能够对数据流进行合理分块,指纹计算和对比开销较小,克服了现有许多分块算法中的不足。
1 可变长度分块算法
数据分块[8]是重复数据删除算法的前提,其性能的优劣直接影响将来重复数据删除算法的好坏。数据分块通常有两种类型:固定长度分块(Fixed-Sized Partitioning, FSP)[9]和可变长度分块(CDC)[10]。FSP将数据分成长度固定的数据块,以同样大小的数据块为单位进行重删,FSP算法对数据修改很敏感,在数据经常变化时效果较差;而CDC根据Rabin指纹算法[11]通过一个特殊大小的滑动窗口依次分割数据,其分块大小随着数据内容的变化而变化,并且修改只会影响到修改数据周围的少量数据,适用于数据经常修改的情况[10]。
CDC算法使用一个特定宽度w的滑动窗口,从数据的开始处以字节长度滑动,当w大小的数据被装载完毕后,计算其指纹(Hash)。算法预先给定两个参数D和r,且r 然而,应用场景不同,待检测的源数据有很大的区别[12]:可能是文本数据或图像数据,也可能是结构化数据或非结构化数据,还可能是压缩数据或无压缩数据等;并且源数据中重复部分的数量和分布也有很大差别,不重复内容、少量重复的内容和大量重复的内容共存,使分块大小难以选择;而且目前的大多数分块算法对所有场景均使用相同的分块策略,使其在面对大规模复杂类型数据时性能往往不理想,通常表现出以下几点不足: 1)滑动窗口w的大小难以选择。w的大小直接影响分块的大小,由于重复数据删除的数量和所需的时间与块大小呈负相关,在实际的应用环境中,使用较小分块大小来提高重删率是不可行的。 2)需要预先人工设定参数D和r,选取不当将导致分块效果较差。 3)指纹计算和对比开销较大。CDC算法使用Rabin算法进行数据分块时,滑动窗口每滑动一字节,需要复杂多项式取模一次来计算指纹,边界条件取模一次来确定块边界,并且产生大量的无用指纹,严重影响了重复数据删除的性能。 4)分块边界条件难以满足。fmodD=r的分块边界条件会因为参数设定和待检测数据的特征而出现很难满足条件的情况,直接造成分块过大而使用硬分块,严重时甚至退化为FSP,或者出现大量细碎分块,加大元数据和索引的开销。 本文算法针对CDC算法的以上不足,首先利用分块大小预测模型,得出最佳分块大小;然后设计了编码指纹代替Rabin指纹;最后,在确定分块边界条件时,提出了指纹字符串匹配的分块算法来代替CDC算法中利用参数边界条件的方式,并使用Winnowing算法计算文件整体指纹时的方法快速选择指纹对比模式串。算法不仅解决了分块大小难以控制的问题,同时不用设置参数,计算开销较小,本文算法的结构如图1所示。 图1 本文算法整体框架 Fig. 1 Framework of the proposed algorithm 本文针对CDC算法分块大小的局限性,引入了预测模型。许多研究发现,现有的众多分块技术在选择平均分块大小时都是基于几何分布[13]的。王龙翔等[14]论证了内容分块算法中预期分块长度对重复数据删除率的影响。Hirsch等[15]提出了一种以自然方式控制块大小分布的方法。实验结果证明,该算法的均值和标准偏差非常接近于常数变化,对于变量概率,标准偏差要小得多,大多数值均接近平均值。应用于不同截止条件的分布图呈刺猬形,并且带有一个基本的高斯钟形曲线。因此算法能够较准确地预测平均分块大小,本文算法使用该分块模型预测预期分块大小,过程如下。 1)设L表示给定块的长度,是一个随机变量,它的期望值即为预期分块大小。得到块大小L(L≥M)的概率是第一次M实验失败的概率,l表示指数范围内当前块大小M的上界,M满足以下关系: (1) 2)当L≥M时的概率可以用以下公式求出: (2) 3)从中可以得到当L=M时的概率: Pr(L=M)=Pr(L≥M)-Pr(L≥M-1) (3) 4)则使用以下公式来计算给定条件时的预期块大小w: (4) 通过该分块预测模型获得的预期大小w,避免了参数设置的人为干涉,一定程度上解决了CDC算法中分块大小难以控制的问题。 针对CDC算法使用Rabin算法计算数据块指纹时的计算开销较大等问题,引入了Winnowing算法[16]。该算法在2003年由Schleimer等提出,经常用于检测文件或网页中的相同内容,来判断抄袭[17]等行为。本文使用Winnowing算法来计算指纹是因为该算法以数字ASCII/文字Unicode编码作为指纹,计算开销非常小,并且指纹的构成简单,便于以后的指纹对比操作。DWFM中在映射指纹时,使用w单位大小对待检测数据进行分组,其中w是由2.1节中分块预测模型计算所得到的预期分块大小,使用Winnowing算法计算数据块指纹的过程如下。 1)设待检测数据流D(D中含有n个字符),使用预测大小w对D中所有长度为w的块进行指纹映射,如块C1(C1包含字符1至w)可映射为Hash(C1),同样地,C2(C2包含字符2至w+1)可映射为Hash(C2),则共产生了n-w+1个指纹,Hash(C1),Hash(C2),…,Hash(Cn-w+1)。其中指纹Hash(Ci)(i=1,2,…,n-w+1)与块Ci{i,i+1,…,s+w-1}相对应。 2)将n-w+1个子块用以a为基数的整数表示,映射为以a为参数的整数x(0≤x≤bk),设Code(C1)是数据块C1的ASCII/Unicode编码值,即为C1的指纹值Hash(C1),则数据块C1的指纹值Hash(C1)可用以下公式计算: Hash(C1)=Code(C[1])aw-1+Code(C[2])aw-2+…+Code(C[w])=Hash(C[1])+Hash(C[2])+…+Hash(C[w]) (5) 3)C2的指纹值Hash(C2)可以通过以下公式由C1的指纹值直接求得: Hash(C2)=(Hash(C1)-C[1]aw-1)a+ Code(C[w+1]) (6) 4)将n-w+1个指纹Hash(C1),Hash(C2),…,Hash(Cn-w+1)组成指纹序列Hc,通过公式可发现,后一个块的Hash值与前一块的Hash值的相似性较大。这是由于后一块的指纹值是由前一块向后滑动一个字节得到的,且仅需要在前一块Hash值的基础上通过两次加法和两次乘法得到。相比Rabin算法通过两个复杂多项式取模运算来得到Hash指纹,Winnowing算法使用ASCII/Unicode作为指纹较好地降低了计算开销。 本文算法设计了底层指纹字符串匹配的分块算法确定块边界,代替了CDC算法中利用Rabin参数取模来进行分块的方式,因此需要设置模式串Pw。由于Winnowing算法确定全文件指纹的过程是基于文件内容的,并且是从指纹组合中选择指纹信息,其选择结果体现了数据的本身特性,有利于将来的分块与检测。因此将此过程引入到模式串选取的过程中,设计了模式串Pw的选取规则,使Pw的选择更加符合重复数据删除算法的要求。在选择Pw过程中对Hc进行分组时,使用预期分块大小w为分组大小基数,使Pw的选择遵从最佳分块场景,具体的选取规则如图2所示。 图2 模式串Pw的选取过程 Fig. 2 Selection of pattern string Pw 1)对于待检测数据流D{1,2,…,n}的Hash值序列Hc,以w大小的滑动窗口长度沿着Hc滑动,得到指纹分组h1,h2,…,hi; 2)对于每一个指纹组hm(m=1,2,…,i,i为指纹组个数),取其组内最小的哈希值作为该组的代表,若连续的多个块具有相同的最小值,则选择最右侧的一组; 3)将最小值组成长度为w的序列,作为下一步分块时的模式串Pw,算法描述如下。 算法1 模式串选取算法(Pattern String Selection Algorithm, PSSA)。 输入 待检测数据流D; 输出 模式串Pw。 1) BEGIN 2) 将D使用预测分块大小w进行分块 3) FOR eachCido //对于每一个字块Ci 4) Hash(Ci)=getCode(Ci); //对每个长度为w的块取其编码值作为Hash值 5) Hc=add(Hash(Ci)); //生成指纹字符串序列Hc 6) 将Hc使用w大小进行分组; 7) FOR eachHashwdo //对每个指纹分组Hashw 8) hmin(i)=getMinhi(); //找出每组指纹Hashw中的最小值hmin(i) 9) Pw=add(hmin(i)); //将所有最小值指纹组合形成长度为w模式串 10) END CDC算法进行数据分块时,基本原理和最大的弊端都是需要预先设定参数D和r,当指纹值f与D进行模运算后结果等于r时才建立分块。然而,一方面参数选择依据和准确性很难确定;另一方面边界条件在实际应用中常常会因为参数选择不当等问题出现长时间不能满足的情况,只能在最大可容忍范围Cmax处进行硬分块,甚至退化成FSP算法。且应用场景不同,其数据的特性也相差很多,为不同类型的数据使用相同的参数选取策略是不严谨的。 而Rabin指纹算法寻找分块边界时最底层原理是字符串匹配问题[18]。因此本文算法从其底层原理出发,摒弃设置参数和分块条件等,将数据分块问题转化为指纹字符串的匹配问题,设计了指纹串匹配分块算法。结合上述求出的数据块指纹Hash(Ci)(i=1,2,3,…,n-w+1),使用模式串Pw,进行块指纹和模式串Pw的匹配。DWFM在映射指纹、选择Pw和滑动窗口大小时均使用预测大小w作为基准,是为了使分块大小和结果都体现最佳分块大小时的特性。 当某一块Ci(i=1,2,3,…,n-w+1)的指纹Hash(Ci)与模式串Pw的指纹值Hash(Pw)匹配成功时,在此块的右侧边界创建一个分块。若超过分块大小上界Cmax都未能匹配成功,则在Cmax处创建分块。 在匹配过程中,可以使用Sunday[19]等字符串匹配算法来加速匹配,当匹配失败时,能够尽量多地跳过不可能匹配的字符,Sunday匹配过程如图3所示。 图3 Sunday算法匹配过程 Fig. 3 Matching process of Sunday algorithm Rabin算法在分块时每滑动一字节需要模运算判断一次,不满足分块条件时也不能跳过数据;相比之下,本文的分块算法不仅无需设置参数,而且处理速度较快。指纹串匹配分块算法描述如下。 算法2 指纹串匹配分块算法(Chunking Algorithm based on Fingerprint Matching, CAFM)。 输入 数据块指纹序列Hc; 输出 分块序列Cki。 1) BEGIN 2) d=0; //d代表当前滑动窗口所滑过的字符长度 3) WHILE(d≤Cmax&&窗口内的字符长度等于w) //当d的长度小于分块上界Cmax //w代表滑动窗口的大小即预期分块大小 4) sliding window, matching fingerprints use Sunday; //使用Sunday算法进行指纹串匹配 5) IFHash(Ci) ==Hash(Pw) THEN; //当数据块Ci的指纹等于模式串Pw的指纹 6) create a new chunkCki; //若块指纹与模式串指纹匹配成功,则建立分块 7) window come toCkinext position; //滑动窗口来到块Cki的下一个位置 8) d=0; //将d的长度置为零 9) ELSE 10) skip characters not possible to match; //向右滑过尽可能多的不匹配字节 11) d=d+skip.length; //d的长度变化为d的长度加上滑过的长度skip.length 12) IFd>CmaxTHEN; 13) Ci==Cmax; //Cmax范围内没有匹配成功,则在Cmax处进行硬分块 14) creatCki //其中i=1,2,…,k,k代表分块个数 15) window come toCkinext position; 16) d=0; 17) END 对待检测数据D使用CAFM算法进行分块后,设计了Winnowing指纹串匹配的重复数据删除算法(DWFM)。使用MD5算法[20]为每一个数据块生成一个独一无二的指纹,由于MD5指纹具有唯一性,且无论任何人对数据作了任何修改,即使是很小的改动,其MD5值也会发生很大变化,因此MD5值能够准确检测数据块是否重复,保证重复数据块检测结果的正确性。 在进行重复数据删除时,将每一个待检测块的指纹值MD5(Di)(i=1,2,…,k)与存储或备份系统中的数据块进行指纹对比。若待检测数据块Di的指纹与系统中某一块的指纹完全相同,则说明Di为重复数据块,直接删除不予存储,并更新索引表,将该块的引用次数加1;否则,说明系统中没有与Di内容重复的数据块,则将Di存储到系统中,并在元数据表中维护一条Di的信息。 实验使用Java语言实现了DWFM,测试在Windows环境下进行,操作系统为Windows 7 Ultimate,硬件环境为Intel Pentium CPU G3200 @ 3.00 GHz处理器,4 GB内存容量,500 GB的SAS硬盘,千兆以太网。实验模拟构建了一个客户端和一个服务器节点,为了检验对不同的文件类型采用不同的分块策略下的算法性能,实验采用了多种类型的真实数据集,包括:TXT、DOC、HTML、PPT、PDF、VMDK等。其中,TXT、DOC、PPT、PDF类型数据由AWS、Google以及Twitter数据平台获取,包括大量的用户状态、影评和公开信息;HTML数据集从微博中爬取,信息的多次转发具有重复性;VMDK数据集采用ubuntu8.04与14.04两个版本。获取的不同类型数据集的大小和数量相近,方便对实验结果进行统一化分析。另外,同一类型数据的内容为同一领域,保证了数据之间具有相似性和重复性。实验数据集如表1所示。 表1 实验数据集Tab. 1 Datasets of experiment 实验具体内容:在服务器端存放由表1中数据集组成的文件集合A,每次实验分别使用FSP、CDC和CAFM分块算法对A进行分块,形成原始数据。改变A的内容存放在客户端,使其与A有重复率r,形成待检测数据集B。随机连续地从客户端向服务器端发送文件,并采用与服务器端相同的分块算法分块后进行重复数据删除。实验验证了不同分块算法对不同类型数据重删率的影响,以及不同重复率r时的算法时间。 为了验证重复数据删除算法的效果,实验设置了重复删除率:R=重复删除数据量/原始数据总量,重删率实验结果如图4所示。无论采用哪种分块的重复数据删除算法都能在一定程度上减少数据的最终存储量;除VMDK类型外,对于所有类型的文件,DWFM的重删率都要高于FSP与CDC算法。例如对TXT数据,DWFM重删率高于FSP算法13.557%,高于CDC算法10.289%。由于DWFM对数据进行分块预测,根据数据自身的类型和特性来选择合适的分块大小,因此其分块效果更加符合重复数据删除的边界条件,使得算法的重删率较其他两种算法高出很多。三种重复数据删除算法对TXT、DOC、HTML和VMDK类型的文件重删效果都较好,而对PPT和PDF类型的数据相对较差,这主要是因为PPT类型中的数据形式多变,且位置随意,需要对数据进行严格的预处理,因此影响了重删率。 图4 不同文件类型的算法重删率对比 Fig. 4 Comparison of deduplication rates for different file types 为了验证不同重复率r以及重复分布情况对重复数据删除性能的影响,对TXT数据集进行了相同数据集、不同重复率下的处理时间实验,实验结果如图5所示。DWFM处理时间较短,且处理时间随r的增加呈下降趋势,逐渐趋近于FSP。当重复率r为0.7时,DWFM相对CDC算法改进最大,处理时间缩短了15.6 min,算法性能提升了18.31%。 图5 不同重复率r时的算法时间对比 Fig. 5 Algorithm time comparison at different rate r 结合理论分析和实验结果,对DWFM的复杂度进行全面分析,结果如表2所示,DWFM所消耗的时间复杂度包括以下几点: 1)CAFM在进行数据分块之前,需要通过预测模型选取最佳分块大小,由预测算法公式可得,其时间复杂度为Tw=O(n); 2)使用Winnowing算法计算待检测数据流D中每个长度为w的子块的指纹值,其时间复杂度为Th=O(n-w+1),其中n为D中的字符数; 3)选择模式串Pw的时间复杂度Tp=O(i+w-1),其中i代表指纹组个数; 4)使用CAFM和Sunday算法进行分块的时间复杂度Tc=O(n); 5)MD5指纹计算与对比等重复数据检测操作的时间复杂度为Td=O(m),其中m表示需要对比的数据块个数。 因此,DWFM总的时间复杂度T为: T=Tw+Th+Tp+Tc+Td=2O(n)+O(m)+ O(n-w+1)+O(i+w-1) (7) 表2 算法复杂度对比Tab. 2 Algorithm complexity comparison 由表2可得,FSP算法采用固定分块大小,只需分块后计算MD5指纹即可判断是否为重复数据,因此算法时间最短;但由于无法检测到文件内部重复,因此在实际中应用较少。而CDC算法首先需要使用Rabin算法计算指纹,然后利用参数取模条件来寻找分块边界,最后计算MD5指纹来判断重复,且在分块和指纹比对过程中无法跳过数据,只能按字节依次进行判断,因此产生了大量的无用指纹,增加了指纹开销和算法时间。DWFM在分块前需要预测分块大小,产生一定的时间复杂度,但在分块时使用ASCII/Unicode指纹,而非Rabin指纹,计算开销较小;而且利用指纹字符串匹配的方式来确定分块边界,在匹配失败时能跳过尽可能多的字符,较显著地减少了指纹计算次数。综上对比,DWFM拥有更好的应用前景。 本文算法将Winnowing算法引入重复数据删除来减少指纹计算开销,在分块时无需预先设置参数,而是根据Rabin的底层原理,设计了指纹串匹配的分块算法。该算法特别适合用来解决数据块级重复数据删除时的复杂分块问题,尤其是在待检测数据类型多变、重复内容分布不均的情况时,能够得出更合理的分块大小,在文件内部检测到更多的重复数据。通过实验与FSP和CDC算法相比,本文算法分块大小更加准确,计算和对比开销较小,且重复检测没有误判率,拥有更好的应用前景。 参考文献(References) [1] SUN Y, ZENG C Y, CHUNG J, et al. Online data deduplication for in-memory big-data analytic systems [C]// Proceedings of 2017 IEEE International Conference on Communications. Piscataway, NJ: IEEE, 2017:1-7. [2] ZHENG Y, DING W X, YU X X, et al. Deduplication on encrypted big data in cloud [J]. IEEE Transactions on Big Data, 2016, 2(2): 138-150. [3] 熊金波,张媛媛,李凤华,等.云环境中数据安全去重研究进展[J].通信学报,2016,37(11):169-180.(XIONG J B, ZHANG Y Y, LI F H, et al. Research progress on secure data deduplication in cloud [J]. Journal on Communications, 2016, 37(11): 169-180.) [4] BHAGWAT D, ESHGHI K, LONG D D E, et al. Extreme binning: scalable, parallel deduplication for chunk-based file backup [C]// Proceedings of 2009 IEEE International Symposium on Modeling, Analysis & Simulation of Computer and Telecommunication Systems. Piscataway, NJ: IEEE, 2009: 1-9. [5] LI Z B, HE K J, LIN F N, et al. Deduplication of files in cloud storage based on differential bloom filter [C]// Proceedings of 2016 7th IEEE International Conference on Software Engineering and Service Science. Piscataway, NJ: IEEE, 2016: 111-114. [6] 张沪寅,周景才,陈毅波,等.用户感知的重复数据删除算法[J].软件学报,2015,26(10):2581-2595.(ZHANG H Y, ZHOU J C, CHEN Y B, et al. User-aware de-duplication algorithm [J]. Journal of Software, 2015, 26(10): 2581-2595.) [7] WIDODO R N S, LIM H, ATIQUZZAMAN M. A new content-defined chunking algorithm for data deduplication in cloud storage [J]. Future Generation Computer Systems, 2017, 71: 145-156. [8] WANG G P, CHEN S Y, LIN M W, et al. SBBS: a sliding blocking algorithm with backtracking sub-blocks for duplicate data detection [J]. Expert Systems with Applications, 2014, 41(5): 2415-2423. [9] 邓雪峰,孙瑞志,张永瀚,等.基于数据位图的滑动分块算法[J].计算机研究与发展,2014,51(Suppl.):30-38.(DENG X F, SUN R Z, ZHANG Y H, et al. Sliding blocking algorithm based on data bitmap [J]. Journal of Computer Research and Development, 2014, 51(Suppl.): 30-38.) [10] ZHANG Y C, HONG J, DAN F, et al. AE: an asymmetric extremum content defined chunking algorithm for fast and bandwidth-efficient data deduplication [C]// Proceedings of 2015 IEEE Conference on Computer Communications. Washington, DC: IEEE Computer Society, 2015: 1337-1345. [11] SU H N, ZHENG D, ZHANG Y H. An efficient and secure deduplication scheme based on Rabin fingerprinting in cloud storage [C]// Proceedings of 2017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC). Piscataway, NJ: IEEE, 2017: 833-836. [12] 阎芳,李元章,张全新,等.基于对象的OpenXML复合文件去重方法研究[J].计算机研究与发展,2015,52(7):1546-1557.(YAN F, LI Y Z, ZHANG Q X, et al. Object-based data de-duplication method for OpenXML compound files [J]. Journal of Computer Research and Development, 2015, 52(7): 1546-1557.) [13] MIN J, YOON D, WON Y. Efficient deduplication techniques for modern backup operation [J]. IEEE Transactions on Computers, 2011, 60(6): 824-840. [14] 王龙翔,董小社,张兴军,等.内容分块算法中预期分块长度对重复数据删除率的影响[J].西安交通大学学报, 2016,50(12):73-78.(WANG L X, DONG X S, ZHANG X J, et al. Influence of expected chunk size on deduplication ratio in content defined chunking algorithm [J]. Journal of Xi’an Jiaotong University, 2016, 50(12): 73-78.) [15] HIRSCH M, KLEIN S T, SHAPIRA D, et al. Controlling the chunk-size in deduplication systems [C]// Proceedings of the 2015 Prague Stringology Conference. Prague: PSC, 2015: 78-89. [16] SCHLEIMER S, WILKERSON D S, AIKEN A. Winnowing: local algorithms for document fingerprinting [C]// Proceedings of the 2003 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2003: 76-85. [17] LULU L, BELKHOUCHE B, HAROUS S. Overview of fingerprinting methods for local text reuse detection [C]// Proceedings of the 2016 International Conference on Computing and Network Communications. Piscataway, NJ: IEEE, 2016:1-6. [18] MEYER D T, BOLOSKY W J. A study of practical deduplication [J]. ACM Transactions on Storage, 2012,7(4):1-20. [19] 朱永强,秦志光,江雪.基于Sunday算法的改良单模式匹配算法[J].计算机应用,2014,34(1):208-212.(ZHU Y Q, QIN Z G, JIANG X. Improved single pattern matching algorithm based on Sunday algorithm [J]. Journal of Computer Applications, 2014, 34(1): 208-212.) [20] CHO E M, KOSHIBA T. Big data cloud deduplication based on verifiable hash convergent group signcryption [C]// Proceedings of 2017 IEEE 3rd International Conference on Big Data Computing Service and Applications. Piscataway, NJ: IEEE, 2017: 265-270. This work is partially supported by the National Natural Science Foundation of China (61502215). WANGQingsong, born in 1974, M. S., associate professor. His research interests include big data, data mining. GEHui, born in 1991, M. S. candidate. Her research interests include deduplication.2 算法设计
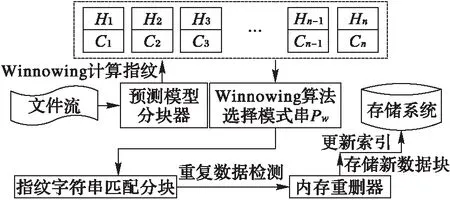
2.1 分块大小预测模型
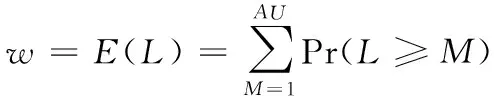
2.2 Winnowing指纹算法
2.3 模式串Pw的设计
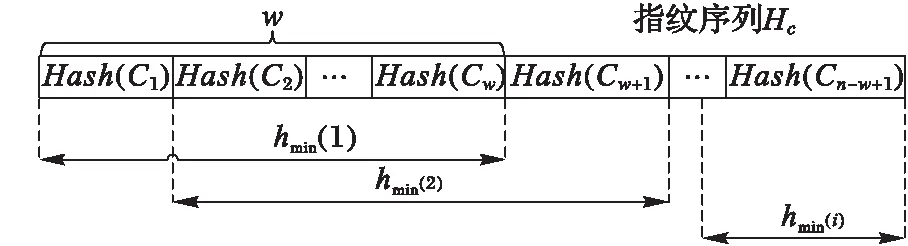
2.4 Winnowing指纹串匹配分块算法

2.5 指纹串匹配的重复数据删除算法
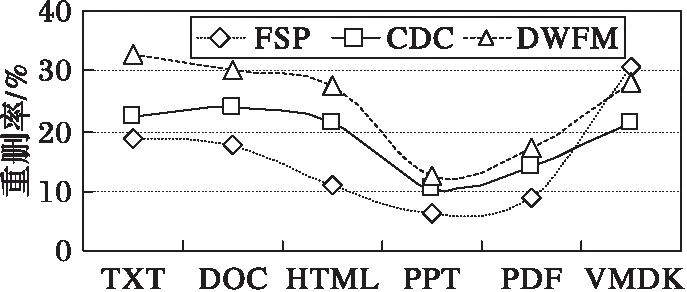
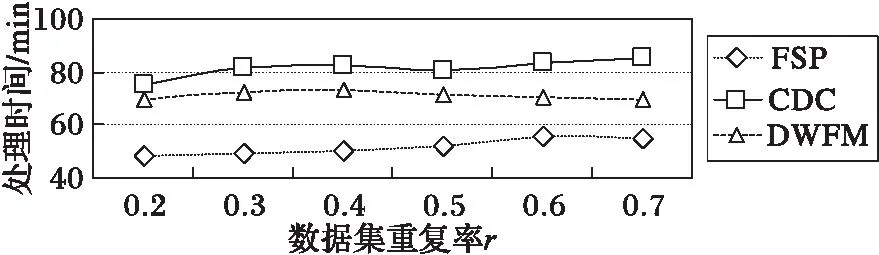
3 算法实验分析和结果
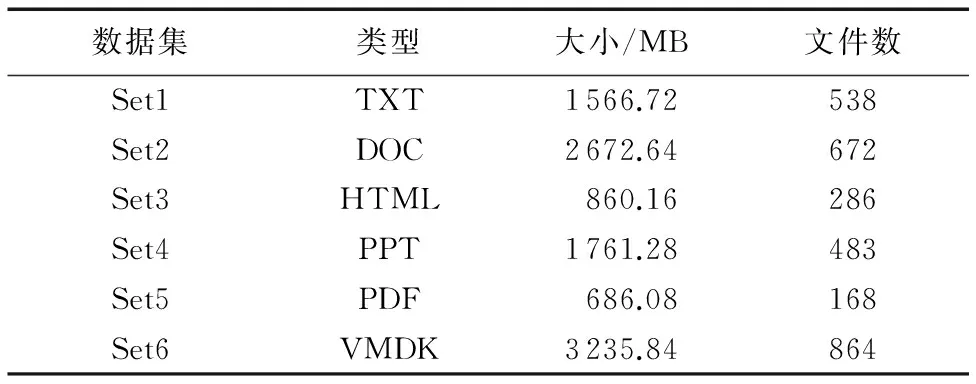

4 结语
