样本量为2的极小样本相容性检验方法
2018-05-21徐颖强陈仙亮曹栋波
徐颖强,陈仙亮,曹栋波
西北工业大学 机电学院,西安 710072
在评估机电产品疲劳寿命及可靠性过程中,根据抽样理论,疲劳试验样本量越大越能体现疲劳寿命的分布特征,疲劳寿命评估的准确度越高[1-2]。然而在航空航天领域,许多高新且昂贵的机电系统疲劳寿命试验样本量通常极少(m=1或2),仅用试验数据对疲劳寿命进行评估结果可信度非常低。
当样本量大于10个时国内外多采用Bayes和Bootstrap等方法进行参数和分布评估[3-8]。而当样本量极少时(m=1或2)可以利用现场试验数据对先验信息数据进行相容性检验将样本扩充到小样本(n≥10)后再进行处理[9-10]。航空航天产品试验前往往能够搜集到包括数字仿真、生物仿真、非全程试验结果、同系列产品试验结果等数据,利用灰色关联度理论等方法进行多源信息融合后方可作为先验信息数据使用[11]。常见的相容性检验方法如Wilcoxon秩和检验和K-S(Kolmogorov-Smirnov)检验多适用于现场试验数据为小样本的情况[12-19]。当现场试验数据为极小样本时,若按照小样本检验过程将先验信息数据和现场试验数据混合在一起检验,由于先验数据大量信息容易湮没现场试验信息,往往检验结果是接受假设,体现不了差异。因此使用传统小样本相容性检验方法处理极小样本问题并不妥当。文献[20-21]针对总体服从正态分布的情形分别提出一种适用于样本量为2的变尺度相容性检验方法;文献[22]提出现场试验数据样本量或先验信息数据样本量为l的条件下非参数检验方法,并对其原理和步骤进行了阐述。
综合上述文献的研究内容,小样本相容性检验方法并不适用于极小样本情况,而极小样本相容性检验方法研究较少,且大多数文献只是直接采用某种方法进行检验,缺乏对方法合理性的详细说明和对不同方法检验功效优劣的比较。航空航天产品疲劳寿命多服从正态分布,因此本文以正态分布作为研究对象,结合Monte Carlo方法,利用两个现场试验数据样本对先验信息数据逐个进行检验,提出一种适用于现场试验数据样本量为2的相容性检验方法。并就Monte Carlo仿真次数对检验功效的影响、先验信息数据样本量对检验功效的影响以及两个现场试验数据分布对检验功效的影响与两种文献方法进行了详细对比和研究分析。对于样本服从威布尔分布等其他情况,也可以参考本文思路进行研究,由于篇幅所限,在此不再展开。
1 两种经典的极小样本相容性检验方法
文献[20]是一种变尺度的检验方法,以两个现场试验数据样本和一个先验信息数据为例进行说明。将两个现场试验样本x1、x2和一个先验信息数据x3混合排序得到次序统计量x(1)、x(2)、x(3),构造统计量
(1)
(2)
给定显著度水平α,当S>α时则以1-α的概率认为现场试验数据和先验分布数据相容。
文献[22]是一种非参数检验方法,以两个现场试验样本和一个先验信息数据为例进行说明。将两个现场试验样本x1、x2和一个先验信息数据x3混合排序得到次序统计量x(1)、x(2)、x(3),其中x3在次序统计量中的位置为j,则在3个数据相容的情况下x(j)的分布函数为
(3)
式中:F(x)为总体分布函数,当现场试验数据样本量较少时可利用自助法进行估计得到,具体方法和步骤见文献[22]。给定显著度水平α,计算满足以下条件的边界值L1、L2。
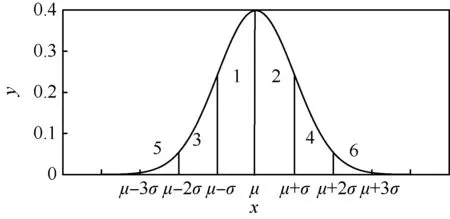
P{xj (4) P{xj>L2}=1-Fj(L2)=α/2 (5) 当L1 假设某个总体服从正态分布N(μ,σ2),根据3σ原则可知样本值分布在±σ范围内的概率为68.26%;分布在±2σ范围内的概率为95.44%;分布在±3σ范围内的概率为99.74%;图1为3σ范围示意图。 图1 3σ示意图Fig.1 Schematic diagram of 3σ 从而可以得到以下推论: 图的±σ1范围在N(μ,σ2)中位置示意图Fig.2 Schematic diagram of ±σ1 range of shown in N(μ,σ2) 图的±2σ1范围在N(μ,σ2)中位置示意图Fig.3 Schematic diagram of ±2σ1 range of shown in N(μ,σ2) 图的±3σ1范围在N(μ,σ2)中位置示意图Fig.4 Schematic diagram of ±3σ1 range of shown in N(μ,σ2) 在上述推论基础上,提出一种具备“自主优化”能力的相容性检验策略,检验流程图如图5所示: 步骤1初始化筛选次数i=1。 步骤3以(μi-σi,μi+σi)为范围筛选剩余的先验信息数据(第一次筛选时剩余的先验信息数据即为所有先验信息数据)。 步骤4判断本次筛选出来的先验信息数据是否为空,如果不为空令i=i+1并返回步骤2;若为空则进入步骤5。 步骤5以(μi-2σi,μi+2σi)为范围筛选剩余的先验信息数据。 步骤6判断本次筛选出来的先验信息数据是否为空,如果不为空令i=i+1并返回步骤2;若为空则进入步骤7。 步骤7以(μi-3σi,μi+3σi)为范围筛选剩余的先验信息数据。 步骤8判断本次筛选出来的先验信息数据是否为空,如果不为空令i=i+1并返回步骤2;若为空则进入步骤9。 步骤9显示全部被筛选出的先验信息数据,程序结束。 图5 相容性检验策略示意图Fig.5 Schematic diagram of strategy for compatibility test 图6 筛选函数自主优化示意图Fig.6 Schematic diagram of independent optimization of filter function 为验证本文提出的基于3σ原则的极小样本相容性检验方法(下文简称为3σ方法)的实际效果,将3σ方法与文献[19]提出的变尺度检验方法(下文简称为文献方法1)和文献[21]提出的非参数检验方法(下文简称为文献方法2)进行对比研究。从正态分布N(μ,σ2)中随机抽取两个数据x1、x2作为现场试验数据,再从中随机抽取t1个数据作为先验信息数据中的“真值”,在正态分布N(μ,σ2)两侧3σ范围以外一定区间内随机抽取t2个数据作为先验信息数据中的“假值”,将t1、t2混合后分别利用3σ方法和两种文献方法对t1+t2个先验信息数据进行相容性检验(设定两种文献方法的显著度水平α=0.1)。定义变量“误差率R”作为评价指标,其中R等于弃真概率和采伪概率之和。 以某飞行器寿命为例进行说明,已知该飞行器寿命服从正态分布N(17 000,2 0002),从中随机抽取两个样本x1、x2作为现场试验数据,随机抽取t1=20个样本作为先验信息数据中“真值”,在N(17 000,2 0002)3σ范围外两个区间[9 000,11 000]和[23 000,25 000]按照均匀分布随机抽取t2=4个样本作为先验信息数据“假值”,因此先验信息数据总数n=t1+t2=24,其中假值所占比例为16.7%。利用Monte Carlo方法对x1、x2进行Nr次重复抽样,分别计算不同仿真次数下上述3种方法的误差率R,结果如图7所示。 当仿真次数少于400次时3种方法的误差率波动较大,而当仿真次数超过400次后误差率逐渐趋于稳定,在上述设定的初始条件下3σ方法误差率最终稳定在14.02%,文献方法1为20.40%,文献方法2为41.76%。因此利用Monte Carlo方法仿真时仿真次数不应低于400次。 图7 仿真次数与误差率关系示意图Fig.7 Schematic diagram of relationship between simulation times and error rate 在3.1节基础上,研究先验信息数据样本量对误差率的影响。为了保证精度,给定仿真次数为1 000次。先验信息数据样本量n由10逐次递增到100,保持其中“假值”所占比例16.7%不变,分别计算不同先验信息数据样本量下3种检验方法的误差率R,结果如图8所示。 如图8所示,随着先验信息数据样本量的不断增加,文献方法1误差率在25%上下浮动,基本保持稳定;文献方法2误差率在40%上下浮动,也基本保持稳定;而3σ方法呈现出误差率随先验信息数据样本量增加而不断下降的趋势,原因在于3σ方法利用相对保守的策略分批次甄别“真值”的同时利用已经确认的“真值”不断修正自身分布函数,使其不断向总体分布函数逼近。由此说明3σ方法具备良好的“自主优化”的能力。 图8 先验信息数据样本量与误差率关系示意图Fig.8 Schematic diagram of relationship between prior information data sample size and error rate 由于现场试验数据样本量只有两个,因此样本的分布对检验效果有较大影响。为了方便描述,将正态分布区域以±σ、±2σ、±3σ为边界划分成6个区域,如图9所示。 将两个样本中的任意一个抽样范围固定在1~6区间的某个区间内,另一个样本抽样范围根据上述正态分布区间划分依次取5、3、1、2、4、6,分别计算每两个区间组合下3种检验方法的平均误差率,仿真次数定为1 000次。(x,y)代表第一个样本抽样区间为x区间,第二个样本抽样区间为y区间。仿真结果如图10所示。 从仿真结果可以看出,由于正态分布中1区间和2区间左右对称,因此x=1和x=2情况下误差率R变化图也呈现左右对称的趋势。同理3、4区间和5、6区间也是如此。当两个样本抽样范围位于同一个区间,即x=y时,3种检验方法的误差率R都达到峰值。具体而言,对于3σ方法,当x=y时误差率R达到最大,且最大值两侧随着两个样本抽样区间距离的不断增加,误差率R快速下降并随后呈现相对稳定的趋势;文献方法一误差率R峰值比3σ方法略低,且随样本抽样区间变化波动更小,但是总体上高于3σ方法误差率R;文献方法3当两个样本位于同一个区间时误差率R高达80%,并且误差率R随样本抽样区间变化呈现出较大的波动性。 图9 正态分布区域划分示意图Fig.9 Schematic diagram of division of normal distribution areas 图10 现场试验数据分布与误差率的关系图Fig.10 Schematic diagram of relationship between experimental data distribution and error rate 1) 当现场试验数据样本量等于2时,仅根据试验结果很难作出有实际意义的寿命评估。在已知寿命服从正态分布情况下,利用本文提出的基于3σ原则的极小样本相容性检验方法可以有效地对先验信息数据进行检验筛选,对样本进行扩充。若样本服从威布尔等其他分布也可以参考本文思路进行研究。 2) 基于3σ原则的极小样本相容性检验方法与两种文献方法相比误差率R总体上更低,检验性能良好。 3) 基于3σ原则的极小样本相容性检验方法检验误差率R随着先验信息数据的增加而不断下降,具备“自主优化”的特性,因此使用该方法时应该尽可能多地收集先验信息数据,当然前提是保证先验信息数据的准确性。 4) 当现场试验数据样本量为2时,两个样本所在区间以及样本之间的相对距离对检验误差率R都会产生一定的影响,因此可以考虑利用专家意见、先验信息等对试验样本分布进行合理估计,并针对不同分布组合采用不同的检验策略。 参 考 文 献 [1] 周兆麟. 数理统计学[M]. 北京: 中国统计出版社, 1987: 4. ZHOU Z L. Mathematical statistics[M]. Beijing: National Bureau of Statistics of China, 1987: 4 (in Chinese). [2] 施雨. 应用数理统计[M]. 西安: 西安交通大学出版社, 2006: 4. SHI Y. Introduction of applied statistics[M]. Xi’an: Xi’an Jiaotong University Press, 2006: 4 (in Chinese). [3] KIJEWSKI T, KAREEM A. Bayes estimation of a langevin mean direction[J]. Communications in Statistics-Simulation and Computation, 2017, 46(4): 2769-2783. [4] FABRICE G, BERNARD D, EMMANUEL U. Reliability estimation by Bayesian methods: Definition of prior distribution from architecture of the system[J]. Reliability Engineering and System Safety, 2013, 82: 299-306. [5] SHONOSUKE S. On bootstrap averaging empirical Bayes estimators[J]. Statistics, 2017, 55(2): 331-357. [7] LI H Y, ZUO H F, SU Y, et al. Study on segmented distribution for reliability evaluation[J]. Chinese Journal of Aeronautics, 2017, 30(1): 310-329. [8] 罗强, 骆飞. 基于Bootstrap法的小样本岩土参数标准值计算[J]. 华中科技大学学报, 2017, 45(8): 93-98. LUO Q, LUO F. Calculating formula for standard value of small-sample geotechnical parameters based on Boot-strap method[J]. Journal of Huazhong University of Science and Technology, 2017, 45(8): 93-98 (in Chinese). [9] 郭荣化, 李勇. 小样本试验中验前数据与现场数据相容性检验方法研究[C]∥第十三届中国系统仿真技术及其应用学术会议论文集. 北京: 中国自动化学会系统仿真专业委员会, 2011: 1115-1121. GUO R H, LI Y. Research on checkout methods for the compatibility test between the pre-test data and the local-test data in small sample test[C]∥Proceedings of 13th Chinese Conference on System Simulation Technology & Application (CCSSTA2011). Beijing: Chinese Association of Automation and System Simulation Committee, 2011: 1115-1121 (in Chinese). [10] 蔡洪, 张士峰, 张金槐. Bayes试验分析与评估[M]. 长沙: 国防科技大学出版社, 2004: 73-74. CAI H, ZHANG S F, ZHANG J H. Bayes test analysis and evaluation[M]. Changsha: NUDT Press, 2004: 73-74 (in Chinese). [11] 陈涛. 小样本条件下风电齿轮传动系统动态可靠性预测方法[D]. 大连: 大连理工大学, 2012: 40-56. CHEN T. Prediction methods of dynamic reliability for wind gear transmission under the conditions of small samples[D]. Dalian: Dalian University of Technology, 2012: 40-56 (in Chinese). [12] 刘冰月, 王景芹. 低压成套开关设备的先验信息相容性检验技术[J]. 东北电力大学报, 2013, 33(1-2): 14-19. LIU B Y, WANG J Q. Compatibility check of the prior information on low voltage switchgear[J]. Journal of Northeast China Institute of Electric Power Engineering, 2013, 33(1-2): 14-19 (in Chinese). [13] 王江元. 验前试验数据与现场试验数据相容性检验方法[J]. 战术导弹技术, 2004(2): 10-12. WANG J Y. Checkout methods for compatibility of pre-test data and locale test data[J]. Tactical Missile Technology, 2004(2): 10-12 (in Chinese). [14] KESELMAN H J, OTHMAN A R, WILCOX R R. The new and improved two-sample test[J]. Psychological Science, 2004, 15: 47-51. [15] 李鹏波, 张士峰, 蔡洪. 导弹仿真试验结果静态一致性检验及其置信度[J]. 现代防御技术, 1999, 27(6): 31-36. LI P B, ZHANG S F, CAI H. Checkout methods for compatibility of pre-test data and locale test data[J]. Modern Defence Technology, 1999, 27(6): 31-36 (in Chinese). [16] 张金槐. 多源信息的 Bayes 融合精度鉴定方法[J]. 国防科技大学学报, 2001, 23(3): 93-97. ZHANG J H. Bayes fusion precision identification method for multi-source information[J]. Journal of National University of Defense Technology, 2001, 23(3): 93-97 (in Chinese). [17] MOSER B K, STEVENS G R, WATTS C L. The two-sample test versus Satterwaite’s approximate F test[J]. Communications in Statistics Theory and Methods, 1989, 18(11): 3963-3975. [18] NEUHAUSER M. Two-sample tests when variances are unequal[J]. Animal Behaviour, 2002, 63(4): 823-825. [19] KASUYA E. Mann-Whitney U-test when variances are unequal[J]. Animal Behaviour, 2001, 61: 1247-1249. [20] 唐雪梅. 小样本场合下相容性检验方法[J]. 系统工程与电子技术, 2001, 23(10): 66-68. TANG X M. Consistency test methods in small sample situation[J]. Systems Engineering and Electronics, 2001, 23(10): 66-68 (in Chinese). [21] 王晖, 潘高田, 臧兴震. 正态分布的小样本数据的相容性检验理论和方法[J]. 数学的实践与认识, 2005, 35(10): 131-137. WANG H, PAN G T, ZANG X Z. Theories and methods of compatibility test on normal distribution with few samples[J]. Mathematics in Practice and Theory, 2005, 35(10): 131-137 (in Chinese). [22] 张湘平, 张金槐. 验前信息与现场字样的相容性检验方法研究[J]. 飞行器测控学报, 2002, 21(1): 55-59 ZHANG X P, ZHANG J H. Study on consistency test methods of pretest information and field subsamples[J]. Journal of Spacecraft TT&C Technology, 2002, 21(1): 55-59 (in Chinese).2 基于3σ原则极小样本相容性检验方法

2.1 检验原理





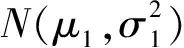

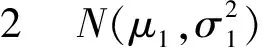
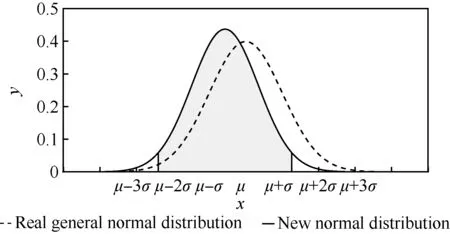
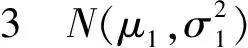

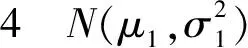

2.2 检验步骤

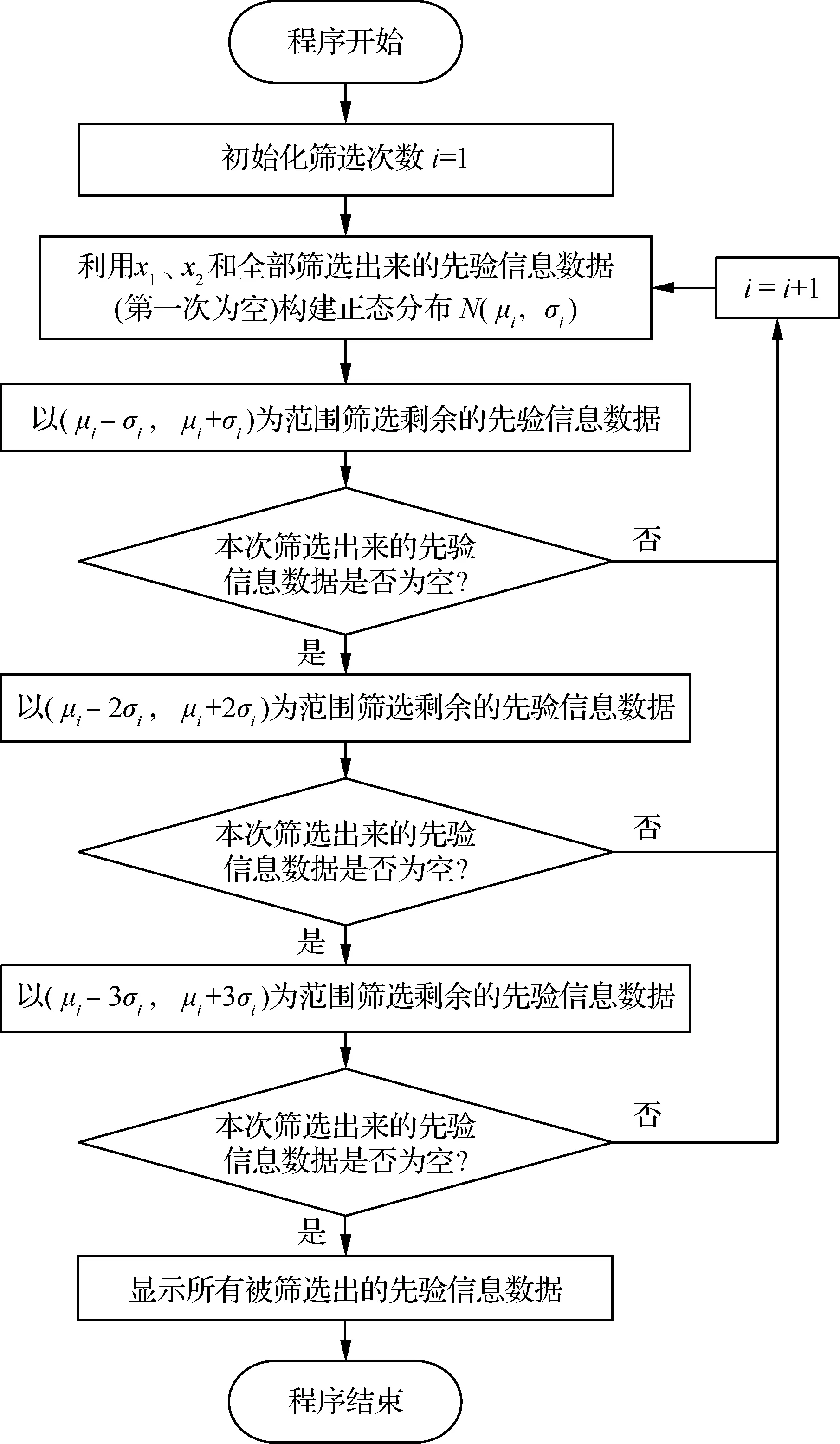


3 基于3σ原则相容性检验方法性能研究
3.1 Monte Carlo仿真次数对检验效果的影响

3.2 先验信息数据样本量对检验效果的影响

3.3 现场试验数据分布对检验效果的影响

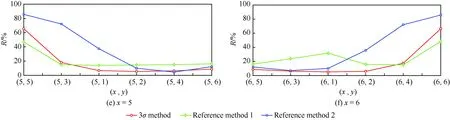
4 结 论
