飞机起落架噪声源定位的压缩感知算法

宁方立，张超，潘峰，刘勇，韦娟

1.西北工业大学 机电学院，西安 710072 2.西安电子科技大学 通信工程学院，西安 710071

随着民航客机数目的增加，飞机在起降过程中的噪声与环境要求产生越来越多的矛盾。针对飞机起降过程中的噪声问题，国际民航组织制订了一系列飞机噪声的适航条例，限制客机的噪声水平[1]。飞机噪声的主要噪声源来自飞机发动机和机体。飞机在降落的过程中，其机体噪声已经和发动机噪声相当，处于同一水平[2]。飞机在飞行过程中，气体流过机身，使得机体表面压力发生扰动，进而产生机体噪声，也称为气动噪声。在机体噪声源中，较为显著的噪声源主要有飞机起落架和增升装置。其中，起落架产生噪声的机理最为复杂，这与起落架的复杂形状有很大关系。Chow等[3]对空客A340进行试验，结果发现起落架噪声比襟翼高6 dB，飞机起落架已成为机体噪声中的主要噪声源。

目前，在闭口风洞或开口射流消声实验室中使用麦克风阵列和波束成形算法已成为起落架气动噪声源分析的重要手段。在国外，Ravetta等[4]在风洞实验室内使用32个麦克风组成的阵列和常规波束成形(Conventional BeamForming, CBF)算法对26%的波音777主起落架缩尺模型进行了试验研究。当频段较高时，能够确定主要噪声源的位置。Li等[5]在常规闭口风洞实验室使用两组56个麦克风组成的阵列和CBF算法对1/4空客340主起落架缩尺模型进行噪声控制效果评估，但在低频段无法进行评估。Quayle等[6-7]在风洞实验室使用两组48个麦克风组成的阵列和基于空间声源相关性的反卷积(CLEAN based Spatial source Coherence,CLEAN-SC)算法研究了起落架结构几何外形与气动噪声的关系，通过修改几何外形达到对气动噪声的降噪处理。Brooks和Humphreys[8]将噪声源强度和阵列测量结果之间建立欠定线性方程组关系，提出采用迭代算法求解该方程组的声源成像反卷积法(Deconvolution Approach for the Mapping of Acoustic Sources, DAMAS)。Blacodon和Elias[9]针对飞机机体的扩展声源，提出欠定线性方程组的谱估计(Spectrum EstiMation, SEM)方法。SEM方法使用非负最小二乘估计获得噪声源分布和噪声源谱。Blacodon[10]随后将SEM方法应用于背景噪声很大的风洞实验室内,对1/11空客320/321缩尺模型进行试验分析。在国内，陈正武等[11]采用36个麦克风组成的口径为1 m的阵列和CBF算法在声学风洞内对翼型气动噪声进行试验研究，获得了在不同迎角下翼型的噪声分布情况。黄迅[12-13]提出了一种实时波束成形算法，能够实时计算出测试时的噪声源分布。以上所述的各类波束成形算法都有不同的缺陷: CBF算法存在主瓣宽度过宽、结果易受旁瓣污染的问题；高级波束成形算法(例如：CLEAN-SC、DAMAS)虽然能在一定程度上弥补CBF的不足，但也会带来别的问题，比如：CLEAN-SC算法时常会出现违背物理规律的负声源[14-15]，而DAMAS算法则会经常有假声源出现[16-17]。

Donoho[18]和Candès等[19]提出压缩感知理论，压缩感知理论最先被用于信号处理领域。压缩感知理论指出，如果一个有限维信号具有稀疏或可压缩表示，那么通过少量的线性、非适应测量，就可以重构出该信号。压缩感知理论自形成以来，被研究学者普遍关注。目前压缩感知已经在超声成像[20]、图像重构[21]及医学[22]等领域得到广泛应用。也有研究人员将压缩感知理论应用在声源定位中。Bai和Kuo[23]采用压缩感知凸优化算法对声源进行定位。Zhong等[24]提出了一种基于采样协方差矩阵的压缩感知算法，用以解决二维声源定位问题。本团队将压缩感知贪婪算法类中的正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法应用于声源定位[25-27]。由于凸优化算法的计算效率低下，并受限于等距约束条件(Restricted Isometry Property, RIP)，而本团队的研究发现OMP算法应用于低信噪比的飞机起落架噪声源定位时结果不稳定，所以将现有压缩感知算法应用于飞机起落架噪声源定位时，会受到较大的约束。

为了克服波束成形算法和压缩感知算法应用于飞机起落架噪声源定位研究的缺陷，本文提出了一种将OMP与奇异值分解(Singular Value Decomposition, SVD)相结合的声源定位算法—OMP-SVD算法。寄期将OMP算法和SVD的优点相结合，能够准确定位飞机起落架气动噪声源。

1 基本理论

1.1 声信号传播模型

图1为声信号传播模型。麦克风阵列为平面随机阵列，阵列中所含麦克风总数为M。对测量平面进行网格划分，将其划分成u×u=N个网格节点，M≪N。在网格节点S处有一声源，由于喷流的影响，会使声信号传播路径发生折射。假设折射点为G点，坐标为(pGx，pGy)。由喷流而导致的传播路径发生折射可视为由一个等效声源产生的影响[28]。等效声源位于声源平面的网格节点S′上，等效声源的声传播路径为图1(a)中由S′指向R的箭头所示。图1中R代表第R个麦克风，坐标为 (pRx，pRy)。由于喷流只在水平方向存在，因此，已知网格节点S的坐标为(pSx，pSy)，则S′的坐标(pS′x，pS′y)与S的坐标之间的关系为

pS′x=pSx+rSS′

(1)

pS′y=pSy

(2)

rSS′=rS′Gv/c

(3)

式中：rSS′为网格节点S与S′之间的距离；rS′G为网格节点S′与折射点G点之间的距离；v为气流速度；c为声音在空气中的传播速度。

图1 声信号传播模型Fig.1 Acoustic signal propagation model

图1(b)中Q为直角三角形的垂足。在△GSS′和△RSS′中，由几何关系可得

rS′G=

(4)

式中：rSG为网格节点S与折射点G之间的距离。

如图1(b)所示，在△RS′Q中，由几何关系可得

(5)

(6)

式中：L1为麦克风阵列到空气和喷流交界面的距离；L2为声源平面到空气和喷流交界面的距离。

求解式(1)～式(6)，可求得网格节点S′和折射点G的坐标。则网格节点S′与麦克风R之间的距离rRS′为

(7)

由于喷流的影响，原始声源所在网格节点S与麦克风R之间的声传播距离rRS将由两部分构成，其计算表达式为

rRS=rSG+rGR

(8)

式中：rGR为麦克风R到折射点G的距离。

建立麦克风阵列到网格节点之间的测量矩阵。测量矩阵的表达式为

(9)

式中：f为声源频率；rij′为等效声源所在网格节点j′与第i个麦克风之间的距离；rij为原始声源所在网格节点j到第i个麦克风的声传播距离。

对声源平面进行网格划分后，假设所有的声源均落在划分的网格节点上。一般情况下声源数目远小于网格节点数。获得麦克风测量值后，将测量数据进行分块处理。再对每个数据块的测量数据作傅里叶变换，得到M×B的测量值矩阵：

y(f)=[Y1(f)Y2(f) …YB(f)]

(10)

式中：Yb(f)=[y1by2b…yM b]T(b=1,2,…,B),B为分块数，yM b为第M个麦克风在第b个数据块的傅里叶变换值。

将矩阵y(f)中每一行的所有值进行平均，得到：

(11)

在实际情况中，由麦克风阵列获得的测量值往往存在一定的误差和噪声。对声源信号和噪声信号同样作分块处理和傅里叶变换后，得到在含噪声情况下，更为准确的声源定位表达模型为

Y=AX+e

(12)

式中：X=[x1x2…xN]T，xN为第N个网格节点的声源信号；e=[e1e2…eM]T为噪声矢量。

1.2 压缩感知理论

由于M≪N，因此式(12)属于欠定方程组，在多数情况下，该方程的解不唯一。又由于实际声源数目远小于网格节点数，所以X为稀疏信号。当声源信号满足稀疏性条件后，通过求解式(13)的约束优化问题，可以重构出声源信号X。

(13)

但是，式(13)的求解属于非确定性多项式难题(Non-deterministic Polynomial-hard, NP-hard)[29]，一般无法直接求解。针对式(13)非凸问题的求解，一种方法就是将该问题转化为凸优化问题[30]，其表达式为

(14)

除了将式(12)进行凸松弛求解，也可以通过贪婪算法寻找该问题的次优解。常用的贪婪算法主要有：硬迭代阈值(Iterative Hard Thresholding, IHT)算法[32]、压缩采样匹配追踪(Compressive Sampling Matching Pursuit, CoSaMP)算法[33]和OMP算法[26]等。OMP算法是一种非线性自适应算法，是经典的贪婪算法，适用于稀疏信号的重构。在每一步迭代中，OMP算法找出测量矩阵中与当前残差最相关的列索引。然后去掉残差中测量矩阵该索引列的贡献，获得新的残差，直到达到最大迭代次数或设定的残差值。OMP算法具有快速收敛、复杂性低等优点。因此本文优先选用OMP算法作为声源重构的算法。

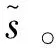
(15)

2 OMP-SVD算法

奇异值分解在信号处理中已有广泛的应用。对测量数据进行奇异值分解后，较大的奇异值包含了信号的大部分信息[34]。利用较大奇异值对应的数据进行重构，既能保证重构精度，又能去除噪声的影响。本文采用奇异值分解对测量数据进行处理。

获得麦克风测量值后，对测量值进行分块处理。分块时，每个数据块包含1 024个数据点，这些数据点包含了所有的频率信息。相邻数据块之间有50%的数据重叠，以保证信号不会失真。将分块后的测量数据组成M×B的测量值矩阵y(f)，对y(f)作奇异值分解处理，可得

y=UΛVT

(16)

式中:U为M×M的酉矩阵；Λ为M×B的对角矩阵，V为B×B的酉矩阵。

当没有噪声存在时，y的秩为K。但噪声是不可避免的，此时y是满秩的。而且y中最大的K个特征向量所对应的空间是噪声空间和真实声源信号空间之和，剩下的特征向量对应的只是噪声空间。

定义一个新的M×K矩阵ySV，其表达式为

ySV=UΛDK=yVDK

(17)

式中：DK=[IK0]T, 其中IK为K×K的单位矩阵，0为K×(B-K)的零矩阵。然后，对声源信号x,噪声项e分别进行分块处理后，再进行奇异值分解，可得

(18)

此时，式(12)可以转换为

ySV=AxSV+eSV

(19)

将ySV、xSV、eSV转换成列向量求解，可得新的表达模型为

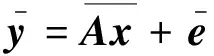
(20)

通过OMP算法，求解式(20)，求解步骤如下[35]：

步骤3找出残差和测量矩阵的列内积绝对值最大的元素，得到测量矩阵中入选原子jt的表达式为

步骤4更新支撑集Λt=Λt-1∪jt。

步骤7判断t是否大于最大迭代次数I，如果是则停止迭代，执行步骤8。否则，令t=t+1，返回步骤3。

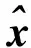
X*=diag(RxSV)

(21)

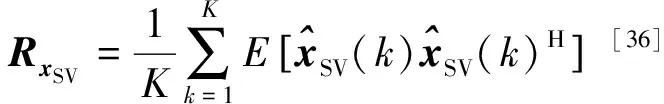
OMP-SVD算法求解声源定位问题步骤如下：

步骤1用阵列采集信号，获得时域下的测量数据。

步骤2将测量数据分块处理，块数为B。对每块数据作快速傅里叶变换，得到声源频率下的测量值y(f)。

步骤3对声源平面进行网格划分，建立测量矩阵A，根据式(12)构建声源定位表达模型。

步骤4对测量数据y、信号x、噪声矢量e进行奇异值分解。将所得矩阵转换成列向量，得到新的声源定位表达模型，如式(20)所示。

步骤6通过式(21)计算声功率X*。

步骤7根据X*中的非零元素所在的行号换算出声源在观测模型中的位置。

3 试验及结果分析

3.1 试验条件

为了验证所提方法的可行性，在全消声室内进行了起落架声源定位试验。麦克风阵列含有24个麦克风，口径为0.8 m，采用随机布局,如图2所示。

图2 麦克风阵列布局Fig.2 Layout of microphone array

如图3所示,试验在全消声室内进行。全消声室的6个表面均由吸声尖劈构成，为试验提供了一个自由的声场空间。消声室地面设工作地网，方便进行试验操作。

图3 全消声室Fig.3 Total anechoic chamber

图4所示为进行试验时起落架的安装情况。起落架放置在喷口的中心平面处，并固定在一块底板上。以起落架中心二维平面为声源平面，在该平面上划分二维网格。麦克风阵列正对着起落架，距离起落架中心平面1.1 m。进行两次试验，喷口处气流马赫数分别为Ma=0.2和Ma=0.1。起落架模型包括：机轮、主支柱和侧支撑3部分。在不同频率下，通过CBF算法、OMP算法与OMP-SVD算法分别对起落架噪声源进行定位，动态范围为10 dB。

图4 起落架安装情况Fig.4 Landing gear installation situation

3.2 Ma=0.2的试验结果

图5为Ma=0.2、f=3 962 Hz下的声源定位结果。当气流马赫数为Ma=0.2时，如图5(a)所示，CBF求解的结果中，起落架声源的主瓣宽度大于反射声源的主瓣宽度。说明起落架声源的声源强度大于反射声源。如图5(b)所示，OMP算法能将反射声源定位，定位的起落架噪声源位置有所偏差。如图5(c)所示，OMP-SVD算法能将反射声源和起落架噪声源定位，起落架声源的声源强度大于反射声源的声源强度。起落架声源强度比反射声源强度大2.34 dB。OMP-SVD算法的结果与CBF算法的结果保持一致，证明了OMP-SVD算法的准确性。同时，与CBF算法相比，OMP-SVD算法可以有效地减少主瓣宽度，抑制旁瓣的影响。

图5 Ma=0.2、f=3 962 Hz下的定位结果Fig.5 Location results for Ma=0.2,f=3 962 Hz

表1给出了OMP-SVD算法在Ma=0.2，f=3 962 Hz下定位的起落架声源和反射声源的相对声压级。

表1Ma=0.2、f=3962Hz下OMP-SVD算法定位的相对声压级

Table1RelativesoundpressurelevelobtainedbyOMP-SVDalgorithmatMa=0.2、f=3962Hz

参数起落架声源强度/dB反射声源强度/dB值0-2．34

3.3 Ma=0.1的试验结果

图6～图9给出了Ma=0.1、不同频率下的声源定位结果。当频率f=3 100 Hz时，如图6(a)所示，CBF算法的结果出现了一个较大的类圆锥形主瓣。类圆锥形的大端位于起落架下方，是底板的反射声源，小端位于起落架上。但由于CBF结果主瓣宽度较宽，不能确定起落架声源的具体位置。如图6(b)所示，OMP算法只能够将反射声源定位，无法定位起落架噪声源。如图6(c)所示，OMP-SVD算法能定位出反射声源和起落架噪声源。此时，反射声源强度大于起落架声源强度，二者相差4.59 dB。在此频率下，OMP-SVD算法的结果与CBF算法的结果保持一致，证明了OMP-SVD算法结果的正确性。同时OMP-SVD算法减小了主瓣宽度，抑制了旁瓣的影响。

当频率升高至f=3 962 Hz时，如图7(a)所示，CBF算法的结果显示出一个类“8”字型的主瓣。反射声源的主瓣宽度大于起落架声源主瓣宽度，说明反射声源的声源强度大于起落架声源的声源强度。如图7(b)所示，OMP算法只能将反射声源定位，无法确定起落架声源的位置。如图7(c)所示，OMP-SVD算法可以定位起落架声源和反射声源。在此频率下，反射声源的声源强度略高于起落架声源的声源强度，二者相差1.58 dB，与CBF算法的结果保持一致。

当频率f=4 392 Hz时，如图8(a)所示，CBF算法的结果已将起落架声源和反射声源分开。此时，起落架声源的主瓣宽度大于反射声源主瓣宽度，说明在此频率下起落架声源强度大于反射声源的声源强度。如图8(b)所示，OMP算法此时的结果已无法准确定位起落架声源和反射声源。如图8(c)所示，OMP-SVD算法能定位出反射声源和起落架噪声源。并且起落架声源的声源强度大于反射声源的声源强度，二者相差3.03 dB，与CBF算法的结果保持一致。

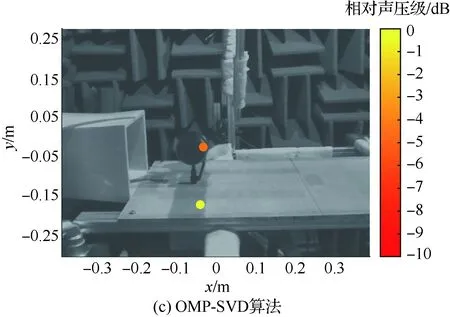
图6 Ma=0.1、f=3 100 Hz下的定位结果Fig.6 Location results for Ma=0.1，f=3 100 Hz

图7 Ma=0.1、f=3 962 Hz下的定位结果Fig.7 Location results for Ma=0.1,f=3 962 Hz

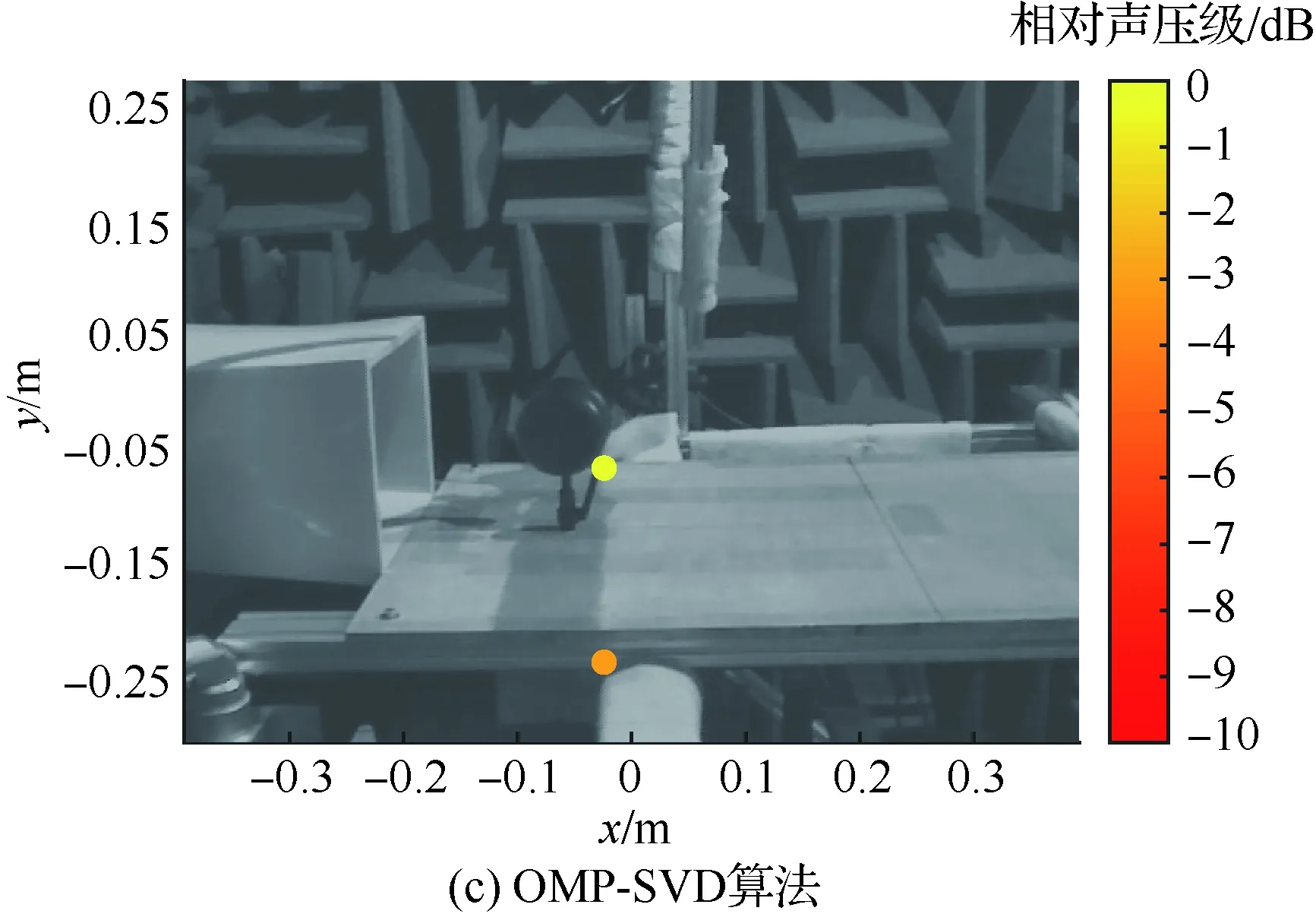
图8 Ma=0.1、f=4 392 Hz下的定位结果Fig.8 Location results for Ma=0.1，f=4 392 Hz

随着频率进一步升高至f=5 555 Hz时，如图9(a)所示，CBF算法结果的主瓣宽度进一步减小。此时，起落架噪声源的主瓣宽度大于反射声源主瓣宽度。但CBF算法结果的主瓣宽度依然较宽，不能确定声源的具体位置。如图9(b)所示，OMP算法能够定位出反射声源，但另一声源也位于底板之上，无法定位起落架噪声源。如图9(c)所示，OMP-SVD算法能定位出起落架噪声源和反射声源。而且起落架噪声源强度大于反射声源强度，与CBF算法的结果一致。此时，起落架声源位于侧支撑柱后方。这是由于侧支柱尺寸小于机轮尺寸，当频率进一步升高后，主要噪声源会向侧支柱移动。

表2为OMP-SVD算法在气流马赫数为Ma=0.1、不同频率下定位的起落架声源和反射声源的相对声压级。

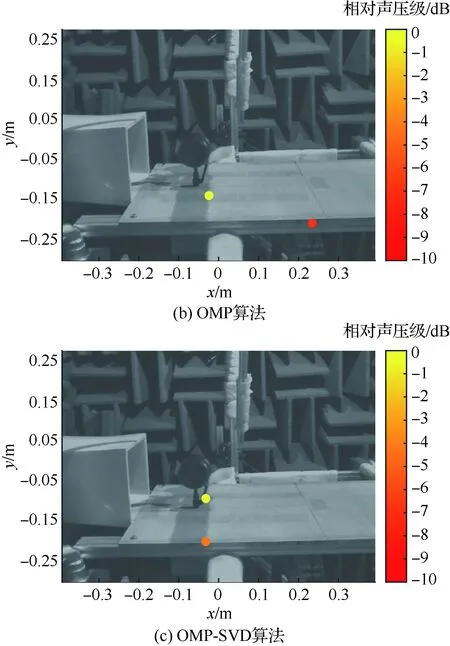
图9 Ma=0.1、f=5 555 Hz下的定位结果Fig.9 Location results for Ma=0.1，f=5 555 Hz

表2Ma=0.1下OMP-SVD算法定位的相对声压级

Table2RelativesoundpressurelevelobtainedbyOMP-SVDalgorithmatMa=0.1

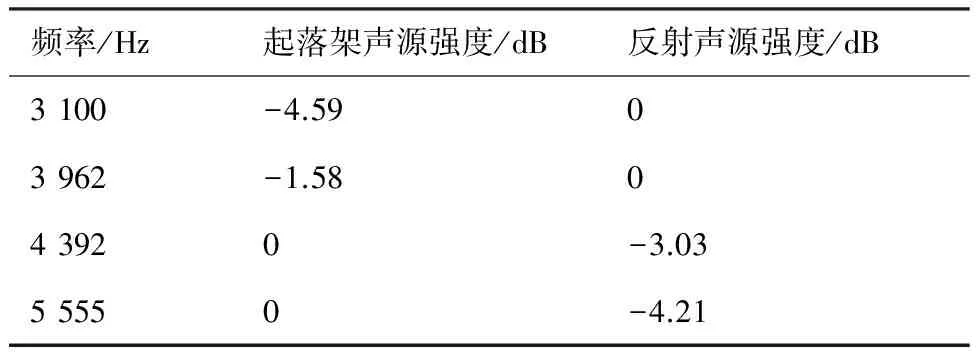
频率/Hz起落架声源强度/dB反射声源强度/dB3100-4．5903962-1．58043920-3．0355550-4．21

4 结 论

通过OMP与SVD算法结合，提出了OMP-SVD算法，研究了气流马赫数为Ma=0.2和Ma=0.1下起落架气动噪声源的位置分布情况。通过在不同频率下的试验，将OMP-SVD算法结果与CBF算法和OMP算法进行对比，验证了OMP-SVD算法应用于起落架气动噪声源定位的可行性。通过综合分析得到以下结论：

1) 随着频率的升高，CBF算法逐渐将起落架噪声源和反射声源分开。主瓣宽度随着频率的升高而逐渐减小。

2) OMP-SVD算法与CBF算法的结果在不同频率下均保持一致,证明了OMP-SVD算法结果的正确性。但相比于CBF算法，OMP-SVD 算法在不同频率下均能够减小噪声源的主瓣宽度，有效地抑制旁瓣的影响。

3) 当气流马赫数降低时，OMP算法的求解结果变差。说明在低信噪比下，OMP算法的结果不稳定。与OMP算法相比，OMP-SVD算法的鲁棒性更好，在不同气流马赫数和频率下的起落架噪声源定位结果均优于OMP算法。

4) 随着频率的升高，起落架噪声源从机轮后方移动至主支柱后方和侧支柱后方。

参 考 文 献

[1] 张卫民, 郝璇, 陈大斌， 等. 大型客机气动噪声预测[J]. 航空制造技术, 2010, 14(7): 66-69.

ZHANG W M, HAO X, CHEN D B, et al. Aeroacoustic prediction of large commercial aircraft[J]. Aeronautical Manufacturing Technology, 2010, 14(7): 66-69 (in Chinese).

[2] DOBRZYNSKI W. Almost 40 years of airframe noise research: What did we achieve?[J]. Journal of Aircraft, 2010, 47(2): 353-367.

[3] CHOW L C, MAU K, REMY H. Landing gears and high lift devices airframe noise research: AIAA-2002-2408[R]. Reston, VA: AIAA, 2002.

[4] RAVETTA P A, BURDISSO R A, NG W F. Wind tunnel aeroacoustic measurements of a 26%-scale 777 main landing gear mode: AIAA-2004-2885[R]. Reston, VA: AIAA, 2004.

[5] LI Y, SMITH M, ZHANG X. Measurement and control of aircraft landing gear broadband noise[J]. Aerospace Science and Technology, 2012, 23(1): 213-223.

[6] QUAYLE A R, DOWLING A P, BABINSKY H, et al. Phased array measurements from landing gear models: AIAA-2007-3463[R]. Reston, VA: AIAA, 2007.

[7] QUAYLE A R, DOWLING A P, GRAHAM W R, et al. Obtaining absolute acoustic spectra in an aerodynamic wind tunnel[J]. Journal of Sound and Vibration, 2011, 330(10): 2249-2264.

[8] BROOKS T F, HUMPHREYS W M. A deconvolution approach for the mapping of acoustic sources (DAMAS) determined from phased microphone arrays[J]. Journal of Sound and Vibration, 2006, 294(4): 856-879.

[9] BLACODON D, ELIAS G. Level estimation of extended acoustic sources using a parametric method[J]. Journal of Aircraft, 2004, 41(6): 1360-1369.

[10] BLACODON D. Array processing for noisy data: Application for open and closed wind tunnels[J]. AIAA Journal, 2011, 49(1): 55-67.

[11] 陈正武, 王勋年, 李征初， 等. 基于声学风洞的麦克风阵列测试技术应用研究[J]. 实验流体力学, 2012, 26(3): 84-90.

CHEN Z W, WANG X N, LI Z C, et al. Application investigation of microphone array measuring and testing technique in anechoic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 84-90 (in Chinese).

[12] HUANG X. Real-time location of coherent sound sources by the observer-based array algorithm[J]. Measurement Science and Technology, 2011, 22(6): 1-9.

[13] HUANG X. Real-time algorithm for acoustic imaging with a microphone array[J]. The Journal of the Acoustical Society of America, 2009, 125(5): EL190-EL195.

[14] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.

[15] SIJTAMA P. CLEAN based on spatial source coherence[J]. International Journal of Aeroacoustics, 2007, 6(4): 357-374.

[16] DOUGHERTY R P. Extensions of DAMAS and benefits and limitations of deconvolution in beamforming: AIAA-2005-2961[R]. Reston, VA: AIAA, 2005.

[17] BROOKS T F, HUMPHREYS W M. Three-dimensional application of DAMAS methodology for aeroacoustic noise source definition: AIAA-2005-2960[R]. Reston, VA: AIAA, 2005.

[18] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[20] WAGNER N, ELDAR Y C, FRIEDMAN Z. Compressed beamforming in ultrasound imaging[J]. IEEE Transactions on Signal Processing, 2012, 60(9): 4643-4657.

[21] DUARTE M F, DAVENPORT M A, TAKBAR D, et al. Single-pixel imaging via compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 83-91.

[22] LUSTIG M, DONOHO D L, SANTOS J M, et al. Compressed sensing MRI[J]. IEEE Signal Processing Magazine, 2008, 25(2): 72-82.

[23] BAI M R, KUO C H. Acoustic source localization and deconvolution-based separation[J]. Journal of Computational Acoustics, 2015, 23(2): 1550008.

[24] ZHONG S, WEI Q, HUANG X. Compressive sensing beamforming based on covariance for acoustic imaging with noisy measurements[J]. The Journal of the Acoustical Society of America, 2013, 134(5): EL445-EL451.

[25] NING F L, WEI J G, QIU L F, et al. Three-dimensional acoustic imaging with planar microphone arrays and compressive sensing[J]. Journal of Sound and Vibration, 2016, 380: 112-128.

[26] NING F L, LIU Y, ZHANG C, et al. Acoustic imaging with compressed sensing and microphone arrays[J]. Journal of Computational Acoustics, 2017, 25(4): 1750027.

[27] 宁方立, 卫金刚, 刘勇, 等. 压缩感知声源定位方法研究[J]. 机械工程学报, 2016, 52(19) :41-52.

NING F L, WEI J G, LIU Y, et al. Study on sound sources localization using compressive sensing[J]. Journal of Mechanical Engineering, 2016, 52(19): 41-52 (in Chinese).

[28] CHU N, MOHAMMAD-DJAFARI A, PICHERAL J. Robust Bayesian super-resolution approach via sparsity enforcing a priori for near-field aeroacoustic source imaging[J]. Journal of Sound and Vibration, 2013, 332(18): 4369-4389.

[29] PAPADIMITRIOU C H. The NP-completeness of the bandwidth minimization problem[J]. Computing, 1976, 16(3): 263-270.

[30] CANDES E J, TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203-4215.

[31] CANDES E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9): 589-592.

[32] MALLAT S G, ZHANG Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.

[33] NEEDEEL D, TROPP J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301-321.

[34] KALMAN D. A singularly valuable decomposition: The SVD of a matrix[J]. The College Mathematics Journal, 1996, 27(1): 2-23.

[35] TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.

[36] CHU N, PICHERAL J, MOHAMMAD-DJAFARI A, et al. A robust super-resolution approach with sparsity constraint in acoustic imaging[J]. Applied Acoustics, 2014, 76: 197-208.