对一道江苏高考题的深入思考与分析
2018-05-18廖香林
廖香林
(四川省仪陇县复兴中学 四川 南充 637668)
1 试题回放
【题目】如图1所示,倾角为α的斜面A被固定在水平面上,细线的一端固定于墙面,另一端跨过斜面顶端的小滑轮与物块B相连,B静止在斜面上.滑轮左侧的细线水平,右侧的细线与斜面平行.A,B的质量均为m.撤去固定A的装置后,A,B均做直线运动.不计一切摩擦,重力加速度为g.求:
(1)A固定不动时,A对B支持力的大小N;
(2)A滑动的位移为x时,B的位移大小s;
(3)A滑动的位移为x时的速度大小vA.
根据题意与所示的图形不得不让人思考这样两个问题:
(1)物体从释放到整个运动的过程中细线是否都是存在拉力;
(2)两物体从释放到整个运动的过程中是否会出现分离.

图1 题图
2 试题解析
2.1 假设法
分别选取A,B作为研究对象,先假设始终存在拉力以及支持力,对A与B进行受力分析如图2所示.

图2 受力分析
不妨设A向左运动的加速度为aA,对于B物体我们根据题意可以认为B的运动一方面跟着A以加速度aA向左加速运动,另一方面B相对于斜面A以加速度a′向下加速,因而B实际的加速度为两者合成,由力的分解与加速度分解合成并结合牛顿第二定律可得
由于假设始终存在拉力以及支持力故绳子长度不变,也即B沿斜面向下运动的距离等于A向左走的距离,所以有aA=a′,联立以上各式可得
(1)由上式不难看出拉力T始终大于零,(与斜面倾角α无关)所以自始至终绳子不会松,与假设相符合(这相当于是一个内部隐含条件,所以题干不需要交代)
(2)但是N并不总是大于零,根据题中条件A和B质量相等,令N大于零,则有
cosα-(1-cosα)2>0
得
当角度α在这个范围内时两物体在运动的过程中不会出现分离,题干中并未交代角度α的取值情况,按道理来说题中应该交代角度α的取值情况,不然本题就不够严谨,但是本题说了A,B均做直线运动那就意味着N不能小于零,因为一旦N小于零,B就不能相对A做直线运动(N小于零则A和B一开始就分离,但由于绳子长度不变,绳子与斜面夹角将不断改变)所以在本题题干叙述情况下本题是很严谨的,并且可以求解.
2.2 物理方法
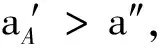

图3 移走细线
则有
(4)
可以看出
所以连接上绳子拉力必不为零,与1中的结论一致.
2.3 变式
下面用2中的这个方法再来判断一个题,如图4所示.

图4 变式
(1)这道题跟上题的区别在于滑轮不在斜面顶端,而通过一根轻杆固定在斜面上使细线不在与斜面平行,已知A和B质量相等,不计一切摩擦,现在将物体与斜面静止释放,释放瞬间细线与斜面夹角为θ,请通过计算判断当θ取何值时,释放后瞬间细线并没有拉紧?(本题用此方法只能判断静止释放瞬间因为释放后每时每刻加速度都在改变,而静止释放后瞬间可以近似认为都是做匀加速直线运动).
解得
3 总结
遇到一些试题时我们应多思考题中的条件以及题干是否具有科学严谨性,即便是高考题我们更应该探究题干背后的隐含条件,以及题干成立物理参数满足什么条件,可以采用假设等方法来进行验证,也可以采用物理方法验证,同一种类型的习题题干变了,可能结果就完全不一样,总之我们要不断探究真理,科学求实.
