CFRP加固砌体填充墙抗燃气爆炸泄爆荷载的优化设计及动力响应

陈 力，郑 康，祝 融，方 秦

(陆军工程大学爆炸冲击防灾减灾国家重点实验室，南京 210007)

砌体填充墙作为最常见的构件形式被广泛应用于建筑外立面围护或内部空间的非结构分割.然而，由于平面外荷载抗力不足，在爆炸载荷作用下，填充墙体极易发生破坏和倒塌，造成大量的人员伤亡和财产损失.近年来燃气爆炸等偶然性爆炸事故频发，如何提高砌体填充墙的抗爆能力，控制破坏危害，是目前建筑抗爆防灾减灾研究领域的一个热点[1-4].FRP材料凭借其轻质、高强度、耐腐蚀、易施工等优点，在工程抗爆外贴加固领域得到了大量的关注和研究[5-7].因此，深入优化FRP外贴加固方案，提高填充墙的抗爆能力，降低加固成本，可以进一步拓展FRP外贴加固技术的应用前景.

结构拓扑优化的历史可以追溯到 1904年Michell[8]提出的桁架理论.而1964年Dorn等[9]将数值方法引入结构拓扑优化领域，使得拓扑优化研究慢慢开始活跃.但是，直到 1988年 Martin等[10]提出均匀化方法，结构拓扑优化设计方面的应用和研究才在相关领域得到重视.Matteo等[11]基于 Tsai-Wu强度准则[12]和均匀化理论[10]进行了一系列拓扑优化计算，提出了FRP加固砌体结构的一种新方法，可以控制设计区域内应力场.Matteo等[13]运用多约束拓扑优化方法，提出了横向荷载作用下 FRP加固墙体的优化步骤，使得FRP加固墙体刚度实现最大化.通过进一步研究[14]他们又基于砌体宏观强度准则，提出了一种基于应力的拓扑优化算法，最大限度地降低了FRP加固的材料成本.然而，以上优化分析成果仅针对静荷载，对爆炸动荷载作用下的响应没有涉及.孟益平等[15]运用基于变密度法的拓扑优化技术和形状优化技术，结合工程设计经验，设计开发了一种新型防爆密闭门.Idris等[16]基于Multi-Island遗传算法[17]和 Hooke-Jeeves算法[18]，对多孔结构的爆炸响应进行了优化，提出了泡沫填充板夹层结构的抗爆优化设计方法.但是，这些研究成果鲜有涉及燃气爆炸泄爆荷载.在泄爆情况下，燃气爆炸荷载特点与炸药爆炸荷载有显著不同，结构响应有明显差异[19-20]，开展燃气泄爆荷载作用下 CFRP加固砌体填充墙的抗爆优化设计、响应与破坏形态研究十分必要.

通过 Hyperworks中的 OptiStruct平台对典型砌体填充墙的 CFRP外贴加固方案进行了抗爆拓扑优化设计，提出了一种优化加固方案.基于优化方案和原型野外燃气爆炸试验，建立了CFRP外贴加固砌体填充墙的精细化数值模型，并讨论了不同加固方式对墙体响应和破坏模式的影响.

1 变密度法拓扑优化原理

结构拓扑优化是通过建立优化设计数学模型，在一个确定的连续区域内寻求结构内部非实体区域位置和数量的最佳配置，使得结构在满足应力、位移等约束条件下，材料的分布达到最优.通过 Hyperworks中的 OptiStruct平台，采用连续体结构拓扑优化方法中的变密度法，基于 SIMP材料插值模型，确定最优的 CFRP材料布局.优化设计有 3个要素：设计变量、目标函数和约束条件.目标函数是设计变量的函数，是用户要求达到的最优设计性能；约束条件是对设计的限制，如对设计变量和其他性能的要求.优化设计数学模型[21]为

目标函数

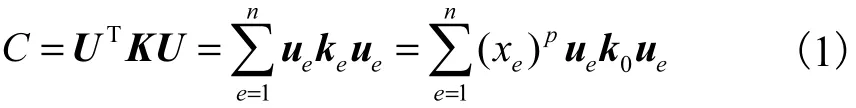
约束条件

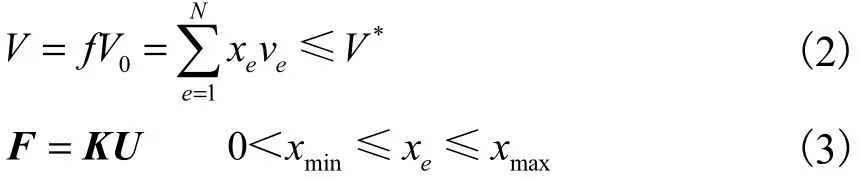
式中：目标函数C定义为结构的总体柔度；F为力向量；U为总体位移矩阵；K为结构总刚度矩阵；V0为整个设计域的初始体积；f为优化体积比；V为优化后的结构体积；ve为优化后的单元体积；xe为设计变量，即单元相对密度；xmin和xmax分别是单元相对密度的最小极限值和最大极限值；ue是单元位移列向量；N为结构离散单元总数；p为惩罚因子；k0为单元刚度矩阵.

优化时，以单元的相对密度为拓扑优化设计变量，其在 0～1之间连续地变化，代表材料的空缺和实体状态.优化求解后，单元密度为1或接近1表示该单元处的材料很重要，予以保留；单元密度为 0或接近 0表示该处材料不重要，予以去除.结构拓扑优化问题就被转换为材料的最优分布问题.OptiStruct平台优化设计流程如图1所示.

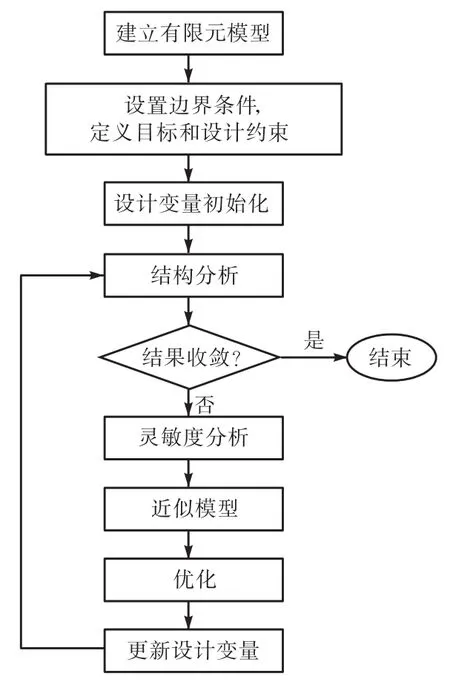
图1 优化设计流程Fig.1 Flow chart of optimization design

2 CFRP外贴加固砌体墙的拓扑优化计算

2.1 优化模型的建立

汪明[22]、韩笑[23]均用分离式模型和等效均匀模型模拟并比较了砌块墙在燃气爆炸荷载作用下的动力响应，发现在小变形情况下，两种模型得出的墙体响应基本一致.由于拓扑优化具有材料无关性，且OptiStruct只能处理线性材料，为提高数值计算效率，采用等效均匀模型，材料均假定为弹性.砌体等效均匀材料密度为 2,100,kg/m3，弹性模量为 3.7,GPa，泊松比为 0.15；CFRP材料密度为 1,800,kg/m3，弹性模量为235,GPa，泊松比为0.17.

图 2为建立的砌体填充墙几何模型，墙体宽、高、厚分别为 2,m、3,m、0.12,m，砌体等效均匀材料单元类型为PSOLID体单元，CFRP加固贴层单元类型为PSHELL壳单元.有限元网格模型如图3所示，墙体和CFRP的单元尺寸均取0.04,m，划分得实体单元11,250个，壳单元 3,750个，两者之间以共节点方式连接.

图2 砌体填充墙几何模型Fig.2 Geometric model of masonry infilled wall

图3 砌体填充墙有限元模型Fig.3 FE model of masonry infilled wall

2.2 优化计算过程

1)设计变量

拓扑优化目的是优化CFRP外贴加固层，使得加固效果不降低的同时，体积最小，得到最优的性价比.设计变量定为设计区域的体积分数，即

该式表达了当前拓扑优化值相对于初始设计空间的分数，为全局响应，取值范围为0～1.0.

2) 优化目标

目标为 CFRP使用量最少，材料消耗率最低，即为CFRP外贴加固层的体积分数最小化.

3) 施加约束

泄爆试验中发现，由于燃气爆炸压力波没有方向性，泄爆时房屋四壁受到均布压力[24]，此时的边界情况类似于周边固支，将模型墙体的约束条件定为4边固支.

4) 位移响应

采用 CFRP外贴加固的目的是防止墙体受到爆炸荷载作用而倒塌.因此，只要 CFRP布未断裂失效，墙体就能维持不倒.基于 CFRP条带的断裂伸长率 1.6%,，可以计算得出位移约束条件，即墙体中心的最大位移为180,mm.

5) 施加荷载

民用住宅发生瓦斯爆炸事故时，超压通常是25～50,kPa，在不利的情况下将达到 100,kPa，威力足以使墙体倒塌.计算时施加荷载为100,kPa的横向均布等效静载.

2.3 优化结果和优化模型

经过 12次迭代并收敛后，优化计算结束.当密度阈值被定义为 0.5时，优化计算结果如图 4所示.图中所示的墙体中心及边界的中部区域所加固的CFRP材料予以保留，计算显示这几处也都是应力集中区域.为了充分发挥 CFRP的性能优势[25]，综合考虑优化结果和CFRP材料的成本和加工需求，设计提出了如图5所示的CFRP外贴加固方案.CFRP条带宽度为 50,mm，条带间距为 50,mm，每面墙的CFRP材料使用量为2.35,m2.

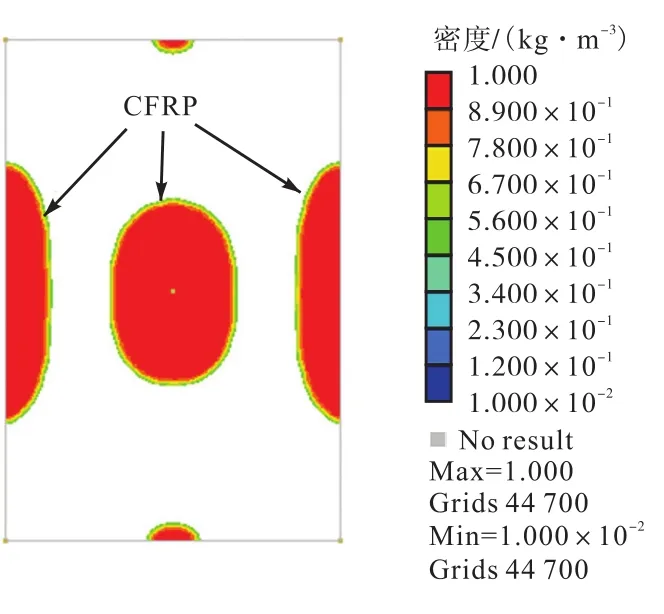
图4 优化结果Fig.4 Optimization result

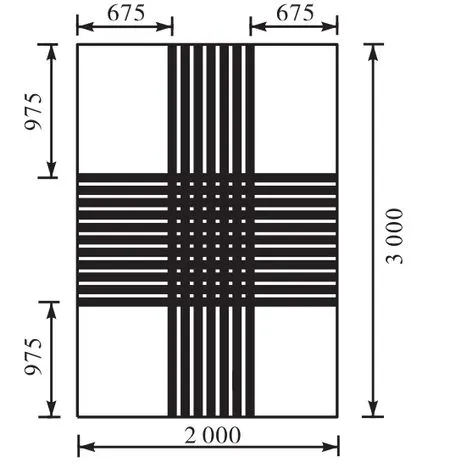
图5 CFRP优化方案Fig.5 CFRP optimization scheme

3 泄爆荷载作用下加固砌体填充墙的动力响应

3.1 加固填充墙的有限元模型

基于ANSYS/LS-DYNA软件平台采用分离式方法建立 1/2砌体填充墙模型.墙体宽度、高度和厚度分别为 2,m、3,m 和 0.115,m.黏土砖块尺寸分别为0.995,m、2.99,m 和 0.115,m，砌筑方式为全顺式.砂浆层厚度为 10,mm.黏土砖和砂浆单元类型均采用SOLID164单元，砖的单元尺寸为0.025,m，砂浆的单元尺寸为 0.005,m.CFRP条带建模厚度为0.111,mm，单元类型采用 SHELL163壳单元，单元尺寸为 0.005,m.CFRP与墙体之间采用共节点方式接触，满足位移协调.

为了形成对比，建立了 3种墙体模型：①未加固墙，如图 6(a)所示，模型共用节点 60,144个，划分实体单元48,950个；②传统的CFRP平均方案加固墙，如图 6(b)所示，模型共用节点 84,294个，划分实体单元 68,820个，壳单元 8,010个；③本文提出的CFRP优化方案加固墙，如图 6(c)所示，模型共用节点90,984个，划分实体单元74,370个，壳单元7,752个.CFRP平均方案加固墙与CFRP优化方案加固墙背爆面粘贴的CFRP面积相同.

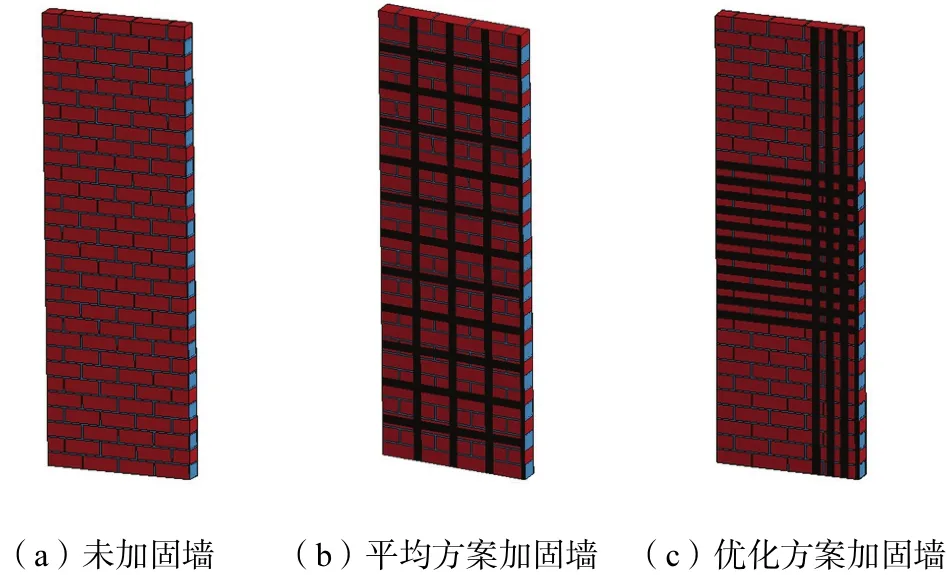
图6 砌体填充墙有限元模型Fig.6 FE model of masonry infilled wall

砌体填充墙使用的烧结多孔砖和砂浆均属于脆性材料，在动载作用下，抗拉强度很低，受损后屈服强度急剧下降.因此，建模时砖和砂浆的材料模型均选用*MAT_BRITTLE_DAMAGE，该模型认为在拉应力作用下，随着单元中微小裂缝的出现，材料的抗拉和剪切强度也随着裂缝的发展延伸而不断降低.采用应变失效准则，参考文献[22-23，26]，数值模型中砖的失效应变为 0.01，砂浆的失效应变为0.005.CFRP条带的应力-应变关系接近线弹性关系，建模时材料模型选用*MAT_PLASTIC_KINEMATIC.材料计算参数如表1和表2所示.

表1 砖与砂浆材料参数Tab.1 Material parameters of brick and mortar

表2 CFRP条带材料参数Tab.2 Material parameters for CFRP

3.2 有限元模型的验证

为了验证建立有限元模型的可靠性，开展了一系列砌体填充墙野外甲烷燃气爆炸试验.试验装置如图 7所示，钢筋混凝土房屋长、宽、高分别为 2,m、2,m、3,m.房屋有一面未进行浇筑，预先埋设24根直径为40,mm的钢制螺柱，用以安装试验墙体.对面墙体中心处预留尺寸为 0.8,m×0.8,m 的窗洞，用以控制泄爆压力.位移计记录试验墙体的横向位移，压力传感器记录作用在墙体上的压力.

用于验证模型的试验工况中甲烷浓度为12.5%,，泄爆窗口密封物为 10,mm 浮法玻璃，试验填充墙采用传统常用的CFRP平均方案加固.试验中测得的泄爆荷载超压时程曲线如图 8所示，由于泄爆口的存在，燃气泄爆爆炸荷载存在一个明显的先上升然后快速下降的趋势；相对于炸药爆炸荷载，燃气泄爆荷载的作用时间更长，作用在墙体上属于均布荷载.

图7 试验装置Fig.7 Test setup

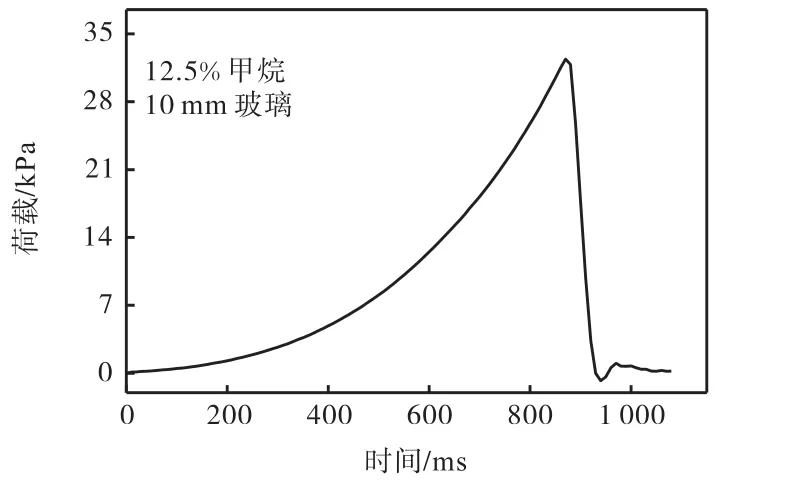
图8 荷载时程曲线Fig.8 Time history of load

采用图 8中荷载数值计算得到的墙体跨中位移时程曲线与试验结果对比如图 9所示.从图 9可以看出，计算得到的填充墙跨中位移峰值、发展时程以及后期振荡均与试验测量结果吻合良好，说明本文建立的精细化有限元模型可以较好地模拟燃气泄爆爆炸荷载作用下填充墙体的动力响应.

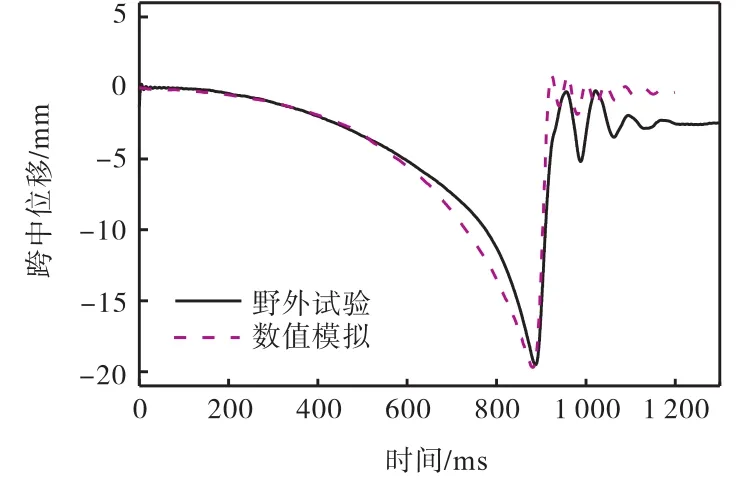
图9 墙体跨中位移对比Fig.9 Comparison of displacement at mid-span of wall

3.3 泄爆荷载作用下加固砌体填充墙的动力响应和破坏形态

分别计算了图 8中的泄爆荷载作用下的未加固墙体、CFRP平均方案加固墙、CFRP优化方案加固墙在燃气爆炸泄爆荷载作用下的动力响应.计算中通过改变SHELL单元厚度来模拟CFRP的粘贴层数，得出的填充墙体的跨中位移最大值如表 3所示.图10为计算得出的不同情况下的填充墙体跨中位移时程曲线.

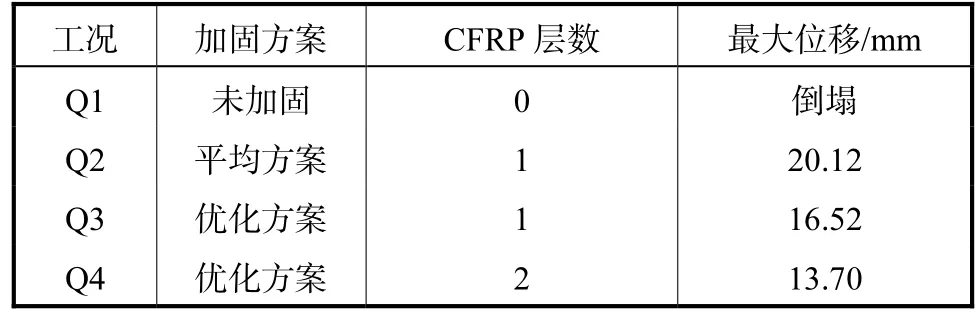
表3 墙体跨中最大位移Tab.3 Maximum displacement at mid-span of wall

图10 跨中位移时程曲线Fig.10 Displacement time histories at mid-span

计算结果显示，在燃气泄爆荷载作用下，未加固砌体填充墙发生了倒塌；而经过CFRP加固的墙体均未倒塌.表 3中，工况 Q3中优化方案加固墙跨中位移最大值较工况Q2中平均方案加固墙少17.9%,.并且优化方案加固墙多贴一层CFRP条带后，跨中位移最大值又减少 17.1%,.计算结果表明，本文提出的优化方案对砌体填充墙的抗爆能力有显著提高.讨论结果发现，增加CFRP条带的粘贴层数可以进一步提高砌体填充墙的抗爆能力.

通过在墙体上下两边施加固定约束，左右不施加约束来模拟单向墙体，计算中不断增大泄爆爆炸荷载峰值，得到的优化加固的单向墙破坏形态如图 11所示.其迎爆面上出现窄X型的裂缝，最终裂缝贯通墙体，并把墙体分割为4份.横向布置的CFRP条带在边界和跨中出现大量断裂，而竖向布置的CFRP条带在上下1/3处及边界处被拉断，与墙体产生裂缝的位置基本相同.

通过在墙体四边施加固定约束来模拟双向墙体.优化加固双向墙破坏如图12所示，可以发现，其墙体发生边界剪切破坏，边界处CFRP条带全部被拉断，墙体被整体推出，且只在墙四角残留少量破碎砖块.计算结果表明，采用 CFRP优化方案加固双向砌体填充墙时，在CFRP条带边界断裂处应予以适当的抗剪加强.

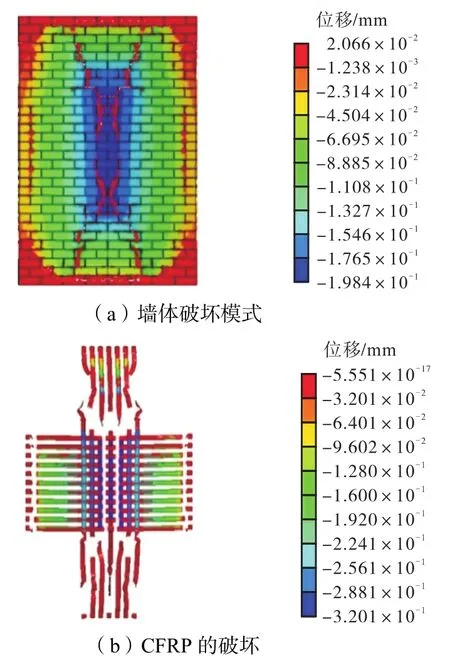
图11 优化加固单向墙破坏模式Fig.11 Failure modes of the optimally retrofitted one-way wall

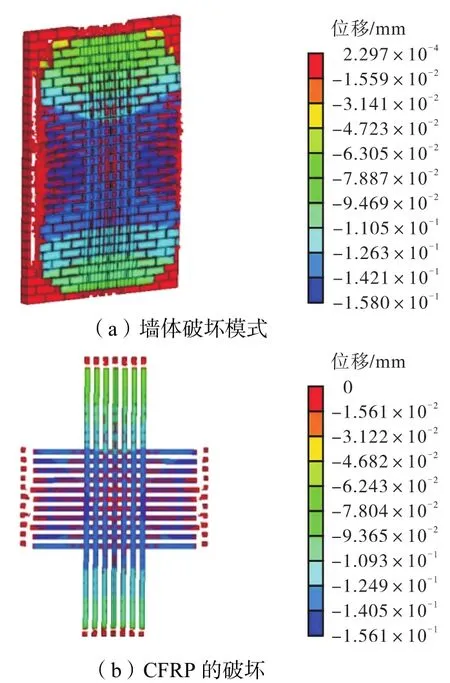
图12 优化加固双向墙破坏模式Fig.12 Failure modes of the optimally reinforced two-way wall

4 结 论

本文针对典型砌体填充墙的 CFRP外贴加固方案进行了拓扑优化设计，建立了相应的精细化数值分析模型，讨论了不同加固方式对墙体响应和破坏模式的影响.

(1) 基于 Hyperworks中的 OptiStruct平台优化，提出了一种新的 CFRP外贴方案.建立了 CFRP外贴加固砌体墙精细化有限元模型，通过野外试验验证了模型的可靠性.

(2) 在相同CFRP使用量的情况下，优化方案加固的砌体填充墙较传统平均方案加固的填充墙抗爆能力提高17.9%,.增加CFRP条带层数可以进一步提高墙体的抗爆能力.

(3) 燃气泄爆荷载作用下，优化方案加固的单向墙体呈窄X型破坏形式，应在四周边界、竖向跨中以及横向1/3处对CFRP条带外贴钢丝网、钢片等予以加强.优化方案加固的双向墙体发生边界剪切破坏，应在四周边界处对CFRP条带予以抗剪加强.

：

［1］ Chen Li，Fang Qin，Fan Junyu，et al. Responses of masonry infill walls retrofitted with CFRP，steel mesh and steel bars to blast loadings[J].Advances in Structural Engineering，2014，17(6)：817-836.

［2］ Shi Yanchao，Xiong Wei，Li Zhongxian，et al. Experimental studies on the local damage and fragments of unreinforced masonry walls under close-in explosions[J].International Journal of Impact Engineering，2016，90：122-131.

［3］ Chen Li，Fang Qin，Jiang Chong，et al. Response and damage level of confined masonry walls to blast[J].Disaster Advances，2013，6(S4)：380-394.

［4］ 张正威，宋二祥，陆新征，等. 核爆冲击波作用下空心砌块墙对主体结构的作用[J]. 工程力学，2008，25(5)：73-78.Zhang Zhengwei，Song Erxiang，Lu Xinzheng，et al.Effects of concrete masonry walls on structures under nuclear blast loadings[J].Engineering Mechanics，2008，25(5)：73-78(in Chinese).

［5］ Mokhtari M，Alavi Nia A. The application of CFRP to strengthen buried steel pipelines against subsurface explosion[J].Soil Dynamics and Earthquake Engineering，2016，87：52-62.

［6］ Sarah L O，Vincent P C，Jared K M，et al. Analysis of CFRP strengthened reinforced concrete structural components subjected to close-in blasts[J].International Journal of Protective Structures，2013，4(4)：467-483.

［7］ 郭樟根，曹双寅，王安宝，等. 化爆作用下 FRP 加固 RC 板的试验研究及动力响应分析[J]. 工程力学，2016，33(3)：120-127.Guo Zhanggen，Cao Shuangyin，Wang Anbao，et al.Dynamic response analysis and test study on FRP strengthened RC slabs subjected to blast loading[J].Engineering Mechanics，2016，33(3)：120-127(in Chinese).

［8］ Michell A G M. The limits of economy of material in frame structure[J].Philosophical Magazine，1904，8(6)：589-597.

［9］ Dorn W S，Gomory R E，Greenberg H J. Automatic design of optimal structures[J].Journal de Mecanique，1964，3：25-52.

［10］ Martin P B，Noboru K. Generating optimal topology in structural design using a homogenization method[J].Computer Methods in Applied Mechanics and Engineering，1988，71：197-224.

［11］ Matteo B，Gabriele M，Alberto T. Design of the optimal fiber-reinforcement for masonry structures via topology optimization[J].International Journal of Solids and Structures，2013，50：2087-2106.

［12］ Stephen W T，Edward M W. A general theory of strength for anisotropic materials[J].Journal of Composite Materials，1971，5(1)：58-80.

［13］ Matteo B，Gabriele M，Alberto T. Simple topology optimization strategy for the FRP reinforcement of masonry walls in two-way bending[J].Computers and Structures，2014，138：86-101.

［14］ Matteo B，Gabriele M. Optimal FRP reinforcement of masonry walls out-of-plane loaded：A combined homogenization-topology optimization approach complying with masonry strength domain[J].Computers and Structures，2015，153：49-74.

［15］ 孟益平，李 博，黄俊旗，等. 基于拓扑优化和形状优化技术的新型防爆密闭门结构设计[J]. 合肥工业大学学报：自然科学版，2015，38(8)：1109-1113.Meng Yiping，Li Bo，Huang Junqi，et al. Structure design of new airtight blast door based on topology and shape optimization method[J].Journal of Hefei University of Technology：Natural Science，2015，38(8)：1109-1113(in Chinese).

［16］ Idris K，Murat Y，Arun S. Designing foam filled sandwich panels for blast mitigation using a hybrid evolutionary optimization algorithm[J].Composite Structures，2016，158：72-82.

［17］ Jansson N，Wakeman W D，Manson J A E. Optimization of hybrid thermoplastic composite structures using surrogate models and genetic algorithms[J].Composite Structures，2007，80：21-31.

［18］ Robert H，Jeeves T A.“Direct Search”solution of numerical and statistical problems[J].Journal of the ACM，1961，8(2)：212-229.

［19］ 陈 力，方 秦，还 毅，等. 爆炸荷载作用下钢筋混凝土梁板结构的面力效应[J]. 工程力学，2010，27(8)：156-163.Chen Li，Fang Qin，Huan Yi，et al. Membrane action on reinforced concrete beam-slab structures subjected to blast loads[J].Engineering Mechanics，2010，27(8)：156-163(in Chinese).

［20］ 方 秦，还 毅，陈 力，等. 应变速率型 RC梁柱显式分析单元及其在 ABAQUS软件中的实现[J]. 工程力学，2013，30(5)：49-55.Fang Qin，Huan Yi，Chen Li，et al. The realization of explicit analytical model of rate-dependent fiber beamcolumn element in ABAQUS[J].Engineering Mechanics，2013，30(5)：49-55(in Chinese).

［21］ Mlejnek H P，Schirrmacher R. An engineer’s approach to optimal material distribution and shape finding[J].Computer Methods in Applied Mechanics and Engineering，1993，106(1/2)：1-26.

［22］ 汪 明. 爆炸荷载作用下钢结构损伤机理及砌体墙破碎过程研究[D]. 天津：天津大学建筑工程学院，2010.Wang Ming. Damage Mechanism of Steel Structures and Fragmentation Process of Masonry Walls Under Blast Loading[D]. Tianjin：School of Civil Engineering，Tianjin University，2010(in Chinese).

［23］ 韩 笑. 燃气爆炸荷载下砖砌墙体的动力响应研究[D]. 西安：长安大学，2012.Han Xiao. The Dynamic Response of Brick Masonry Wall Subjected to Gas Explosion Load[D]. Xi’an：Chang’an University，2012(in Chinese).

［24］ Bao Qi，Fang Qin，Zhang Yadong，et al. Effects of gas concentration and venting pressure on overpressure transients during vented explosion of methane-air mixtures[J].Fuel，2016，175：40-48.

［25］ 郑 康，陈 力，方 秦，等. CFRP布/树脂胶复合条带的抗拉力学性能[J]. 高压物理学报，2017，31(6)：794-802.Zheng Kang，Chen Li，Fang Qin，et al. Tensile properties of CFRP/Epoxy gel composite strip[J].Chinese Journal of High Pressure Physics，2017，31(6)：794-802(in Chinese).

［26］ 韩永利，陈 洋，陈龙珠. 基于 LS-DYNA 的墙体抗燃气爆炸能力数值分析[J]. 防灾减灾工程学报，2010，30(3)：298-302.Han Yongli，Chen Yang，Chen Longzhu. Simulation on anti-blast ability of masonry wall under gas explosion load based on LS-DYNA[J].Journal of Disaster Prevention and Mitigation Engineering，2010，30(3)：298-302(in Chinese).