基于0D/2D耦合的涡扇发动机总体性能计算研究

李 燕，葛 宁

(南京航空航天大学能源与动力学院，南京210016)

1 引言

为提高航空发动机的性能、效率及可靠性，同时缩短研制周期、降低研制成本，全球多个航空发动机研制机构在开发并完善发动机总体性能仿真系统。传统的性能仿真软件，如GasTurb、TURBOMATCH、PYTHIA、T-MATS等，都是以零维(0D)模型为基础，通过热力学平衡方程计算发动机各部件进出口的循环参数，从而得到推力、耗油率等总体性能参数。但这些软件有两个缺陷：①未考虑发动机的几何构型及部件内部气体的流动状况；②非设计点性能预估的精度很大程度上依赖于部件特性图的准确性，而部件特性要么通过通用特性图缩放得到，要么通过大量实验获取。前者太过于依赖经验，计算精度低；后者一旦部件有所改动，就需重新实验来获得部件特性，耗资巨大。

鉴于此，美国在NPSS(推进系统数值仿真)计划中提出了数值缩放技术[1-2]，将发动机内某一部件的高精度模型(三维(3D))和其他低精度模型(0D)耦合在一起进行数值模拟。目前这项技术在国内外均有应用和发展：Reed等[3]将风扇的3D模型集成在传统的0D仿真平台上，实现了0D/3D耦合的发动机整机仿真；陈玉春等[4]将3D尾喷管的CFD计算程序和0D发动机性能计算程序结合在一起，实现了数值缩放技术在发动机混合器和尾喷管中的应用；Mund等[5]借鉴数值缩放技术中构建混合精度模型的思路，从流道设计出发，建立了发动机部分部件(进气道、风扇、外涵)的二维(2D)几何模型，发展了0D/2D耦合的发动机总体性能计算方法。

本文基于S1流面对某型双轴混合排气涡扇发动机低压压气机和低压涡轮进行了初步设计，并将基于周向平均N-S方程的通流模型与T-MATS平台上的0D模型结合起来，改数值缩放技术中的3D高精度模型为2D模型，解决了3D数值模拟计算难度大且耗时长的问题，实现了0D/2D耦合方法在低压压气机和低压涡轮设计中的应用。

2 基于0D/2D耦合的涡扇发动机总体性能计算方法

2.1 0D的T-MATS仿真平台

T-MATS(Toolbox for the Modeling and Analysis of Thermodynamic Systems)是NASA格林研究中心在2014年公开发表的一套用于热力系统建模、仿真及控制的工具箱[6]。作为MATLAB/Simulink平台上的一个子库，其模块化界面清晰明了，使用灵活；内部程序的开源性不仅方便用户创建或优化模块，而且还便于其与用户开发的程序集成。

2.2 基于周向平均N-S方程的2D通流计算

采用课题组开发的通流计算程序[7]，作为发动机部件2D数值仿真和分析的工具。程序以周向平均N-S方程作为控制方程；附加项中，采用Simon模型[8]模拟无粘叶片力，采用分布式损失模型[9-11]模拟粘性叶片力，非设计点的落后角和损失模型采用Miller[12]提出的方法。控制方程求解使用有限体积法，时间离散采用多步Runge-Kutta显示格式[13]。该程序计算速度快，能反映真实子午流场。

2.3 基于0D/2D耦合的涡扇发动机设计点总体性能计算方法

图1为0D/2D耦合计算模型示意图。图中，灰色区域是基于T-MATS平台搭建的0D模型；白色区域是2D通流模型。

设计点求解时，首先由通流计算得出低压压气机S2流面的流场，出口总温、总压经过质量加权平均后代入T-MATS中作为核心机进口边界条件，再将高压涡轮出口参数作为低压涡轮进口条件代入通流计算程序。部件匹配必须保证流量平衡和功率平衡两个守恒条件。其中T-MATS本身通过流量平衡方程和功率平衡方程求解各个部件出口参数，而低压压气机和低压涡轮采用通流程序分别计算，需要验证是否满足平衡条件。具体计算流程(图2)为：

(1)按设计点要求给定低压压气机出口背压p2和低压转速NL，由通流计算得到低压压气机流量w1、功耗Wcl及出口总温、总压。

(2)T-MATS平台上，初设定一个内涵流量和燃油量wf(在0D计算结果附近取值)，计算得到高压涡轮出口总温、总压。

(3)以高压涡轮出口状态作为低压涡轮进口条件，低压转速仍设为NL，按设计点要求设置低压涡轮出口背压，通过通流计算得到低压涡轮流量做功量Wtl及出口总温、总压。

(4)检验是否满足流量平衡和功率平衡条件，如果不满足则分别重新修改和wf，重复步骤(2)～(4)，直到同时满足两个平衡条件。

(5) 通过T-MATS计算外涵、混合器、尾喷管，得到总体性能参数。

2.4 基于0D/2D耦合的涡扇发动机非设计点总体性能计算方法

与设计点计算不同，非设计点计算无设计要求限制，所以除了保证流量平衡和功率平衡外，还需满足混合器进口静压相等，即保证外涵总压与内涵总压之比在0.95～1.05[14]，以减小混合器损失。因此，非设计点计算流程中，选定某一低压转速后，首先初设定一个 p2，执行设计点步骤中的(2)～(4)；然后调整 p2，直到满足压力平衡要求(如图2虚线内指示)，最后执行步骤(5)。

3 低压压气机和低压涡轮的初步设计

利用吴仲华[15]的两类流面理论，假设压气机和涡轮在叶根、叶中、叶尖处存在S1流面，在这3个流面上构造2D叶型，通过重心径向线积叠得到完整叶片，再将得到的初步叶型代入通流计算程序。

3.1 基于S1流面的低压压气机初步设计

低压压气机的初步设计及性能验证参考了Denton等[16]的设计思路，具体方法是：①根据设计要求(表1)和0D算出的低压压气机出口参数，确定压气机的流道和中径处的气流角；②给定等环量分布规律，计算出从叶根到叶尖不同半径处的气流角；③根据气流角，采用双圆弧叶型构造方法设计二维叶型，再通过径向积叠构建三维叶型。

表1 低压压气机初步设计要求Table 1 Preliminary design requirements of the low pressure compressor

初步设计时不考虑叶片的三维特性，不涉及叶片的弯掠，只在叶根、叶中、叶尖3个流面设计二维叶型。通过调整影响压气机性能的轮毂比、压气机进出口马赫数、叶片展弦比、反力度及双圆弧叶型特征参数[17]修改叶型。采用商业软件Numeca验算叶型的气动性能，根据叶片通道内的激波、分离等流场细节不断优化叶型，直到3个S1流面上的气动性能均满足设计要求。表2和图3为S1流面流场计算结果。由图表可知，叶片3个流面的压比和效率与设计要求的误差均在1%以内，各叶排的叶根、叶中、叶尖没有明显的流动分离，满足初步设计要求。因此，该低压压气机叶型可作为0D/2D耦合计算中的2D模型。

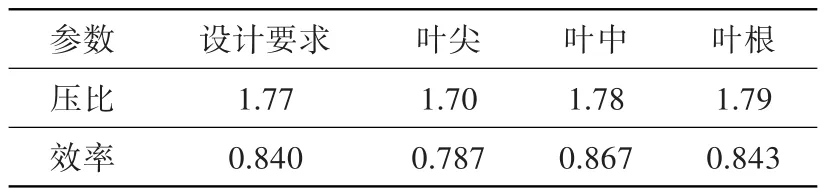
表2 低压压气机S1流面计算结果Table 2 Results of the low pressure compressor on S1 stream surface

3.2 基于S1流面的低压涡轮初步设计

与压气机设计类似，低压涡轮设计也需要确定涡轮的流道、叶片数及叶型。具体途径是：①根据设计要求(表3)及0D计算的低压涡轮进出口参数，得到低压涡轮流道和中径处的气流角；②给定从叶根到叶中为等气流角的分布规律；③根据气流角，采用基于三阶贝塞尔曲线[18]的涡轮叶型参数化设计方法设计二维叶型，再通过径向积叠构建三维叶型。

表3 低压涡轮初步设计要求Table 3 Preliminary design requirements of the low pressure turbine

调整影响涡轮气动性能的轮毂比、涡轮进出口马赫数、叶片展弦比、反力度及贝塞尔曲线5个特征点的参数，不断改进涡轮叶型，直到性能满足设计要求。表4和图4为低压涡轮S1流面流场计算结果。由图表可知，叶片3个流面的落压比和效率与设计要求的误差均在5%以内，且各叶排的叶根、叶中、叶尖没有流动分离现象，满足初步设计要求。因此，该低压涡轮叶型可作为0D/2D耦合计算中的2D模型。

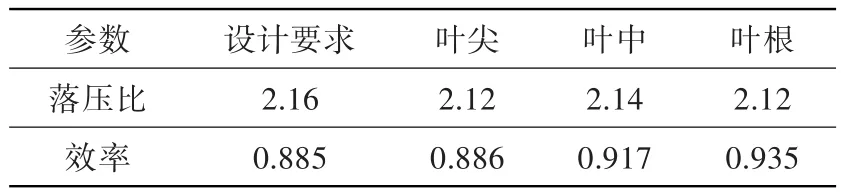
表4 低压涡轮S1流面计算结果Table 4 Results of the low pressure turbine on S1 stream surface

4 0D/2D耦合的涡扇发动机总体性能计算结果

4.1 设计点

根据该型涡扇发动机的要求，选取地面起飞状态为设计点。设计点低压转速为11 300 r/min；低压压气机进口压力为101 325 Pa，温度为288.13 K，出口背压为153 000 Pa；低压涡轮进口压力为362 100 Pa，温度为1 030 K，出口背压为150 500 Pa。

图5为低压压气机S2流面相对马赫数分布。可看出第一级和第二级转子有一道较强激波，整个流场无明显分离。表5则显示周向平均后的通流计算结果与设计要求误差均在±5%以内。

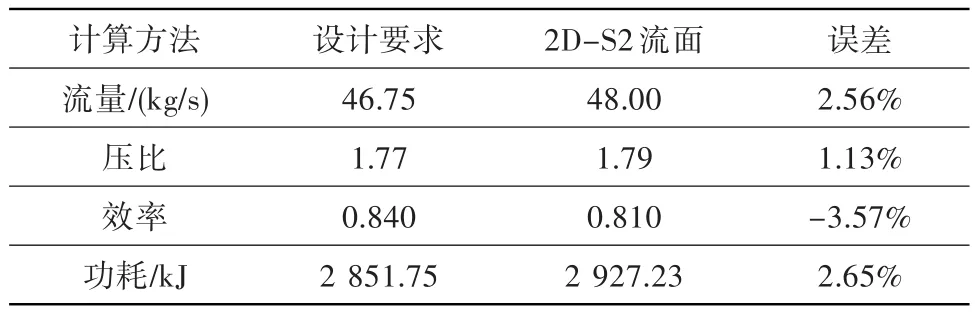
表5 低压压气机S2流面计算结果Table 5 Results of the low pressure compressor on S2 stream surface

图6为低压涡轮S2流面相对马赫数分布。由图可知，整个涡轮都处在亚声速状态，无明显分离。结合表6可见周向平均后的通流计算结果与设计要求误差在±5%以内。

表7为发动机设计点总体性能计算结果与实验结果的对比。可见，0D/2D耦合计算得到的耗油率、推力等性能参数与实验结果之间的误差均在5%以内。这说明该耦合模型精度满足工程要求，可用于非设计点性能计算。

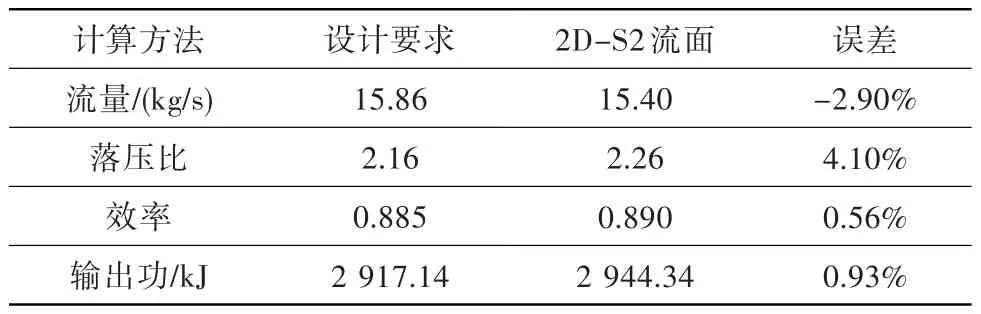
表6 低压涡轮S2流面计算结果Table 6 Results of the low pressure turbine on S2 stream surface

表7 涡扇发动机设计点总体性能计算结果Table 7 Simulation results of turbofan engine overall performance on the design point

4.2 非设计点

非设计点计算时，假设发动机几何不可调，通过调节燃油量控制涡轮前温度，从而求解发动机共同工作线以及非设计点总体性能。0D/2D耦合计算采用上述方法，确定了除1.0转速外的其他5个转速下的共同工作点，每个工作点都至少需20次迭代。0D计算则是利用T-MATS缩放通用特性图得到性能结果。

图7为采用不同方法得到的低压压气机共同工作线。通过对比可知：0D计算以及0D/2D耦合计算得到的喘振裕度均与实验值很接近。图8为非设计点总体性能对比。由图可知：同一涡轮前温度下，推力、燃油量、涵道比均有差异，说明三者对应的热力学平衡状态不同。但相对于0D计算，0D/2D耦合的计算结果更接近实验值。其中推力的预估精度平均提高了3.96%，涵道比的预估精度平均提高了1.20%，燃油量的预估精度平均提高了2.74%，这表明0D/2D耦合方法可提高涡扇发动机总体性能预估精度。但0D/2D耦合计算也存在误差，这主要源于初步设计的部件和真实部件的差异。由于受压气机设计方法的限制，本文设计的低压压气机特性线与原部件特性线有偏差(图7)，并且该低压压气机非设计点的效率均低于实验结果，所以叶型仍有待优化。

5 结论

(1)基于S1流面初步设计的涡扇发动机低压压气机和低压涡轮的叶型满足要求，可用于建立0D/2D耦合模型。

(2)在T-MATS平台上，结合基于周向平均N-S方程的通流计算程序，实现了0D/2D耦合方法在涡扇发动机总体性能计算中的应用。该方法考虑了流动过程中的粘性效应和流动损失，真实反映了低压压气机和低压涡轮内部的流动特性，使得总体性能计算精度比0D的更高。

(3)作为数值缩放技术的简化应用，0D/2D耦合计算方法不仅能较为准确地预估发动机的总体性能，还便于部件设计人员快速评估叶型变化对总体性能的影响，具有工程应用价值。

参考文献：

[1]Follen G，Aubuchon M.Numerical zooming between a NPSS engine system simulation and a one dimensional high compressor analysis code[R].NASA/TM-2000-209913，2000.

[2]John K L，Gregory F，Cynthia N，et al.Numerical propulsion system simulation review[R].NASA/TM-2002-209795，2002.

[3]Reed J A，Afjeh A A.Distributed and parallel program⁃ming in support of zooming in numerical propulsion sys⁃tem simulation[C]//.Proceeding of Symposium on Applica⁃tions of Parallel and Distributed Computing.USA：1994.

[4]陈玉春，黄 兴，高本兵，等.发动机总体与尾喷管三维并行设计研究[J].航空动力学报，2007，22(10)：1695—1699.

[5]Mund F C，Doulgeris G，Pilidis P.Enhanced gas turbine performance simulation using CFD modules in a 2D repre⁃sentation of the low-pressure system for a high-bypass tur⁃bofan[J].Journal of Engineering for Gas Turbines and Pow⁃er，2007，129(3)：761—768.

[6]Chapman J W，Lavelle T M，May R D.Toolbox for the modeling and analysis of thermodynamic systems user’s guide[R].NASA/TM-2014-216628，2014.

[7]杨晓锋.通流模型在组合压气机分析与设计中的应用[D].南京：南京航空航天大学，2016.

[8]Simon J F.Contribution to throughflow modelling for axial flow turbomachines[D].Belgium：University of Liege，2007.

[9]Horlock J H.On entropy production adiabatic flow in tur⁃bomachines[J].Journal of Basic Engineering，1971，93：587—593.

[10]Bosman C，Marsh H.An improved method for calculating the flow turbo-machines,including a consistent loss model[J].Journal of Mechanical Engineering Sciences，1971，16：25—31.

[11]Hirsch C.Numerical computation of internal and external flows[M].New York：John Wiley&Sons，1988.

[12]Miller D C，Wasdell D L.Off-design prediction of com⁃pressor blade losses[C]//.Proceedings of the Institution of Mechanical Engineers International Conference:Turboma⁃chinery-Efficiency Prediction and Improvement.1987：249—260.

[13]Jameson A，Schmidt W，Turkel E.Numerical solutions of the Euler equation by finite volume method using Run⁃ge-Kutta time stepping schemes[R].AIAA 81-1259，1981.

[14]《航空发动机设计手册》总编委会.航空发动机设计手册：第7册——涡喷及涡扇发动机总体[K].北京：航空工业出版社，2001.

[15]Wu C H.A general theory of three-dimensional flow in subsonic and supersonic turbomachines of axial-,radial-,and mixed-flow types[R].NACA TN 2604，1952.

[16]Denton J D.Multall-An open source,CFD based,turboma⁃chinery design system[R].ASME GT2017-63993，2017.

[17]《航空发动机设计手册》总编委会.航空发动机设计手册：第8册——压气机[K].北京：航空工业出版社，2002.

[18]Ramanamurthy S V，Kumar S K.Development and valida⁃tion of a bezier curve based profile generation method for axial flow turbines[J].International Journal of Scientific Research，2014，3(12)：187.