光滑接触条件下非圆形有压隧洞应力及位移解析解
2018-05-17,,
,,
(华北电力大学 水电与岩土工程研究所,北京 102206)
1 研究背景
由Muskhelishvili[1]提出的平面弹性复变函数方法是一种可以计算隧洞围岩及衬砌中的应力及位移的解析方法,利用这种方法可以较容易地获得无支护复杂洞形隧洞的应力和位移解[3-6]。但是在实际应用中,为了保证隧洞的安全,防止围岩的失稳破坏,常常需要在隧洞周边设置衬砌支护,所以研究带支护的深埋隧洞问题更具有实际意义。Wang等[7]在2009年获得了单个圆洞与环形衬砌相互作用的深埋隧洞的应力和位移解;Lu等[8]在2011年求解了考虑支护滞后过程的圆洞和环形衬砌相互作用深埋有压隧洞问题,他们都是将问题简化为无限域内的平面应变问题求解。对于较复杂的非圆形隧洞封闭式支护的问题,2014年文献[9-10]根据衬砌内边界的应力边界条件及围岩与衬砌接触面上的应力和位移连续条件,分别利用柯西积分解法和幂级数解法求解了隧洞和衬砌的应力场和位移场。
在解决带支护的深埋隧洞问题时,上述研究成果在求解过程中都认为围岩与衬砌之间的接触为完全接触。然而,在隧道施工过程中,由于衬砌浇筑时压力不足或者围岩与衬砌之间的刚度相差较大时,围岩和衬砌之间就不满足完全接触的条件。文献[11]在求解带衬砌的深埋非圆形隧洞问题时,就假定围岩与衬砌之间的接触为完全光滑接触的情形,并利用幂级数解法获得了隧洞和衬砌的应力场和位移场,并且得出了光滑接触条件下衬砌内边界的最大切向应力较完全接触条件小的结论。完全光滑是指当围岩和衬砌产生滑动时,法向的正应力和位移是连续的,切向的剪切应力也连续且为0。但切向的位移可以是不连续的,也就是说接触界面上的应力矢量和法向位移满足连续条件,但可以允许围岩与衬砌之间产生滑动。同时,文献[9]引用位移释放系数η模拟衬砌的支护滞后过程,η可由支护断面和掌子面之间的距离来确定[12-13]。
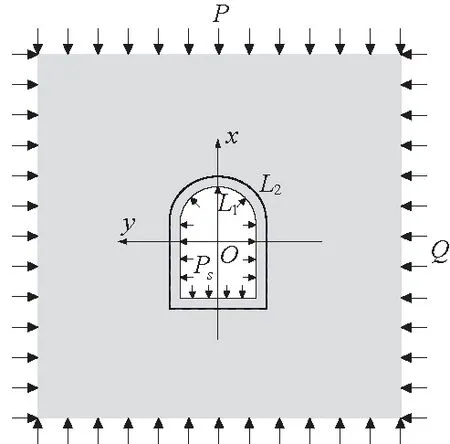
图1 地应力和内水压力 共同作用下的非圆形隧洞Fig.1 A non-circular tunnel subjected to in- situ stress and internal water pressure
不管是完全接触还是光滑接触,目前的复杂洞型都没有考虑隧洞内部的内水压力。实际上,深埋水工隧洞在工程实际中的应用十分广泛,比如引黄入晋工程南于线7号隧洞最大埋深近400 m,锦屏二级水电站引水隧洞最大埋深更是达到了2 400 m,所以求解有内水压力的深埋隧洞问题具有重要的现实意义。
本文将在平面应变假定的前提下,利用复变函数方法,求解衬砌与围岩光滑接触且隧洞内有内水压力时非圆形水工隧洞(图1)的应力和位移解。
2 求解的基本原理及方程
2.1 围岩和衬砌的应力及位移分量求解
在进行地下非圆形隧洞封闭式支护的应力计算时,通常把围岩与支护的相互作用视为弹性理论的平面接触问题,此时的整体式支护可当作镶嵌于弹性无限体内的环状弹性体。对于本文提出的问题,使用复变函数解法中的保角变换方法进行应力分析,该方法通过引进映射函数z=ω(ζ),将物理平面(z平面)上形状比较复杂的支护横断面变换到象平面(ζ平面)上边界形状比较简单的圆环区域。将z平面上的隧洞外部映射到ζ平面上的圆外域时,其映射函数的普遍形式可用式(1)表示[2]。
(1)
式中R,ck为复常数,限制孔型大小和形状。
围岩和衬砌上的应力组合表达式为[14-15]:
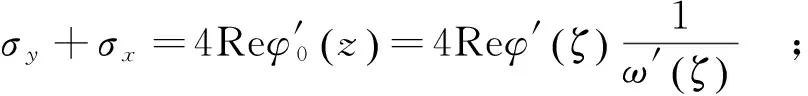
(2)
ω″(ζ)φ′(ζ)]/[ω′(ζ)]2} 。
(3)
式中:σx,σy,τxy为直角坐标系下的应力分量;i为虚数单位;Re为求实部;符号“—”代表共轭;φ0(z),ψ0(z)是围岩或者衬砌在z平面的2个解析函数,通过式(1)的映射函数可以求得在ζ平面内以ζ为自变量的2个解析函数,即:
(4)
(5)
同时,围岩和衬砌上的位移分量的表达式(也是位移边界条件的表示式)[14]为
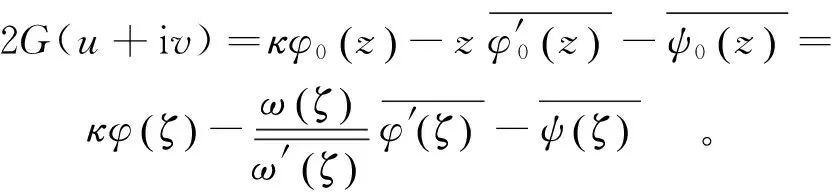
(6)
式中:G为剪切模量;κ=3-4μ,μ为泊松比;u,v分别为x,y方向的位移分量。
本文为了能够考虑光滑接触条件,采用正交曲线坐标系下的应力和位移分量,由式(2)、式(3)可以得出在z平面内正交曲线坐标系下的应力和位移分量[14]。其中,应力分量的转换可以利用弹性力学中的转轴公式求得,即
(7)
τxysin(2α) ;
(8)
式中σρ,σθ,τρθ为z平面内正交曲线坐标系下的应力分量。
因此有:
σθ+σρ=σx+σy,
(10)
σθ-σρ+2iτρθ=(σy-σx+2iτxy)e2iα。
(11)
式中 e为自然指数, e2iα=cos(2α)+isin(2α)即欧拉公式。
其中,
(12)
最终得到:
(13)
(14)
位移分量的表达式为
(15)
式中uρ,uθ分别为z平面内正交曲线坐标系下法向和切向位移分量。
2.2 围岩和衬砌的解析函数形式
在2.1节中已经得出了用2个解析函数φ(ζ)和ψ(ζ)表示的围岩和衬砌在正交曲线坐标系下应力和位移分量的表达式。因此,要求得围岩和衬砌的应力和位移分量,必须先求得围岩和衬砌各自对应的2个解析函数。
隧洞在开挖完成到稳定之前,假设没有支护,围岩会完成相应的位移,此时围岩对应的解析函数为φ1(ζ),ψ1(ζ)。本文考虑支护滞后的隧洞开挖过程,隧洞位移完成最大位移的η(0≤η≤1)倍后进行支护,围岩和衬砌相互作用,在衬砌单独作用下,围岩对应的解析函数为φ2(ζ),ψ2(ζ)。φ3(ζ),ψ3(ζ)则是围岩对衬砌作用后,衬砌对应的解析函数。
围岩开挖后未支护时围岩的解析函数φ1(ζ),ψ1(ζ)的表达式为[2]:
(16)
(17)
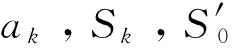
考虑支护滞后的过程时,将z平面上围岩映射到ζ平面单位圆的圆外域,所以φ2(ζ),ψ2(ζ)只有负幂次项,它们可表示为:
(18)
(19)
式中bk,dk是待求常数。
将z平面上衬砌映射到ζ平面的圆环内,所以φ3(ζ),ψ3(ζ)既有正幂次项,也有负幂次项,它们可表示为:
φ3(ζ)=e0+e1ζ-1+…+enζ-n+…+f1ζ1+…+
(20)
ψ3(ζ)=g0+g1ζ-1+…+gnζ-n+…+h1ζ1+…+
(21)
式中ek,fk,gk,hk是待求常数。
若支护结构也关于x轴对称,则bk,dk,ek,fk,gk,hk都是待求的实常数。这些常数应根据边界L1上的应力边界条件和L2上的光滑接触条件求得。
2.3 求解围岩和衬砌解析函数的基本方程
利用L1上的应力边界条件和L2上的光滑接触条件,可以获得求解φ2(ζ),ψ2(ζ)和φ3(ζ),ψ3(ζ)的基本方程。

在围岩和衬砌的接触面上,根据法向位移连续条件,可以得到
(22)
(23)
式中:κ1=3-4μ1;G1=E1/[2(1+μ1)];E1和μ1分别是岩体的杨氏模量和泊松比。
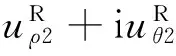
(24)
(25)
式中:κ2=3-4μ2;G2=E2/[2(1+μ2)];E2和μ2分别是支护材料的杨氏模量和泊松比。
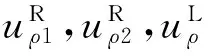
(26)
在接触面上ζ=σ。
在围岩和衬砌的接触面上围岩的法向应力和衬砌的法向应力相等,围岩的剪应力和衬砌的剪应力也相等,在ζ平面上其应力连续条件可表示为
(27)
式中σ=ρeiθ,ρ=1,θ为ζ平面上的极角。
同时,在接触面上围岩和衬砌为完全光滑接触,所以它们的剪应力不仅是连续的,且应该都为0。由此,根据应力边界条件在z平面用正交曲线坐标系下的分量来表示的另一种形式[14],在边界上给出σρ=N,τρθ=T,其中N,T是ρ,θ的函数,则
2(Ν-iT)=2σρ-2iτρθ=σρ+σθ-
(σθ-σρ+2iτρθ)。
(28)
由此可得
(29)
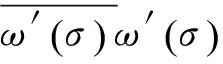
(30)
式中Im为求虚部。
将衬砌内边界L1映射到ζ平面上圆环内边界γ1,其应力边界条件的复变函数表示为
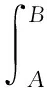
(31)
式中Xn,Yn为x和y方向的面力的合力。同时,应力边界条件在直角坐标系下的表达式为
Xn=lσx+mτxy;
(32)
Yn=lτxy+mσy。
(33)
当衬砌内边界作用内水压力Ps时,σx=σy=Ps(规定以压为正),τxy=0,代入式(32)、式(33)可得:
(34)
(35)
式中l,m分别为外法线的方向余弦。
由此可得

Psω(σ1)+常数 。
(36)
将式(36)代入式(31)可得衬砌内边界L1在静水压力Ps作用下在ζ平面上的应力边界条件,即
(37)
在衬砌内边界上σ1=R0σ(R0为根据映射函数得出的控制衬砌厚度的实数),代入式(37),则得
Psω(R0σ)。
(38)
至此,我们获得了求解φ2(ζ),ψ2(ζ),φ3(ζ),ψ3(ζ)的基本方程,即式(26)、式(27)、式(30)、式(38)。
2.4 围岩和衬砌解析函数的求解过程
本文使用幂级数解法求解φ2(ζ),ψ2(ζ),φ3(ζ),ψ3(ζ),取级数为有限项,令式(18)—式(21)中的最高次幂为N。这样b0,d0,e0,g0,bk,dk,ek,fk,gk,hk(k=1,2,…,N)就一共有6N+4个未知量待求。
(39)
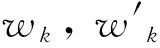
因为σj和σ-j的虚部只差一个负号,这样就可以列出N个方程。
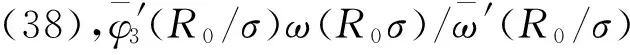
(40)
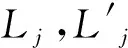
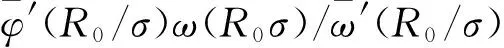
(41)
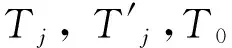
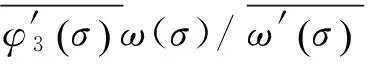
最后,因支护对围岩的影响随着ζ的增大而减小,当ζ→时(对应z平面无穷远处),则由式(15)可得
(42)
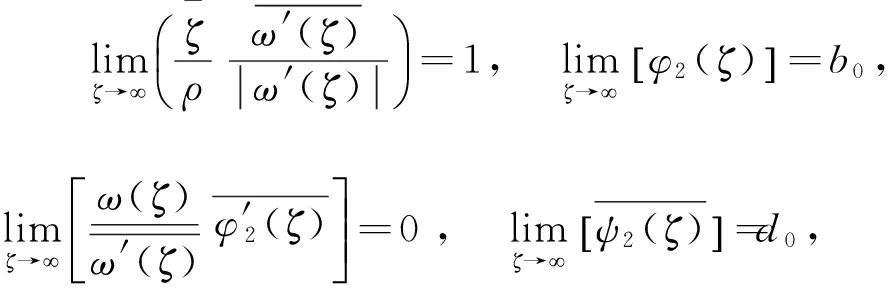
κ1b0-d0=0 。
(43)
这样再加上由式(26)列出的N+1个方程,一共就得到6N+4个方程,编写程序求解计算出b0,d0,e0,g0,b1,…,bN,d1,…,dN,e1,…,eN,f1,…,fN,g1,…,gN,h1,…,hN这些待求的未知量,从而可以确定φ2(ζ),ψ2(ζ)和φ3(ζ),ψ3(ζ)这些解析函数。
3 围岩和衬砌的应力和位移求解
3.1 围岩和衬砌应力的求解
在确定了φ2(ζ),ψ2(ζ)和φ3(ζ),ψ3(ζ)以后,可以求解围岩和衬砌的应力和位移。
用φ3(ζ),ψ3(ζ)代入式(13)、式(14)可以求得衬砌内的应力。在求解围岩的应力时需要同时考虑没开挖隧洞之前围岩所对应的复势函数,支护前开挖隧洞对围岩造成的影响以及衬砌对围岩的影响,这样,式(4)、式(5)中的φ(ζ)和ψ(ζ)就可以分别表示为:
(44)
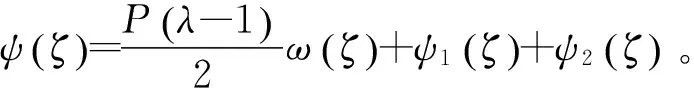
(45)
再将φ(ζ)和ψ(ζ)代入式(13)、式(14)就得到围岩内的应力。
3.2 围岩和衬砌位移的求解
支护后,衬砌的位移uρL,uθL可直接根据式(25)求出,围岩的位移uρR,uθR可根据式(46)求出,即
(46)
4 算例和分析
以直墙半圆拱形隧洞为例,衬砌厚度为1 m,取n=8,所求得的映射函数为[16]
z=ω(ζ)=7.545 61(ζ-0.074 99+0.120 76ζ-1+
0.045 36ζ-2-0.065 13ζ-3+0.020 83ζ-4+0.001 18ζ-5-
0.002 85ζ-6-0.000 96ζ-7-0.002 21ζ-8)。
(47)
由式(47)可知:R=7.545 61,c0=-0.074 99,c1,…,c8等于ζ负幂次项前面的系数,所求得的R0=0.885 69。给定的计算参数为E1=20 GPa ,E2=30 GPa,μ1=μ2=0.2,P=10 MPa,Q=5 MPa,即侧压力系数λ=0.5,内水压力Ps=1 MPa。
当地应力分量P,Q为压应力,若计算时所输入的值为正值,则为正值的σρ,σθ表示压应力,为负值时表示为拉应力。直墙半圆拱形隧洞以x轴为对称轴,取θ=[0°,180°]作图,θ=0°对应直墙半圆拱隧洞拱顶,θ=180°对应隧洞底板中点。
4.1 计算精度检验
取N=100来求解方程,可以得到较好的结果。在检验衬砌内边界的应力边界条件时,我们取位移释放系数η=0.2。因为位移释放系数η=1时,围岩与衬砌之间没有相互作用,所有的边界条件都能精确满足,不需要进行讨论。η的值越小,围岩与衬砌之间的作用力越大,所以这里取η=0.2,对边界条件的满足程度进行检验。
在衬砌内边界ρ=R0上,若σρ=Ps,τρθ=0,则可以精确满足L1上的应力边界条件,其结果如图2(a)所示。
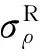
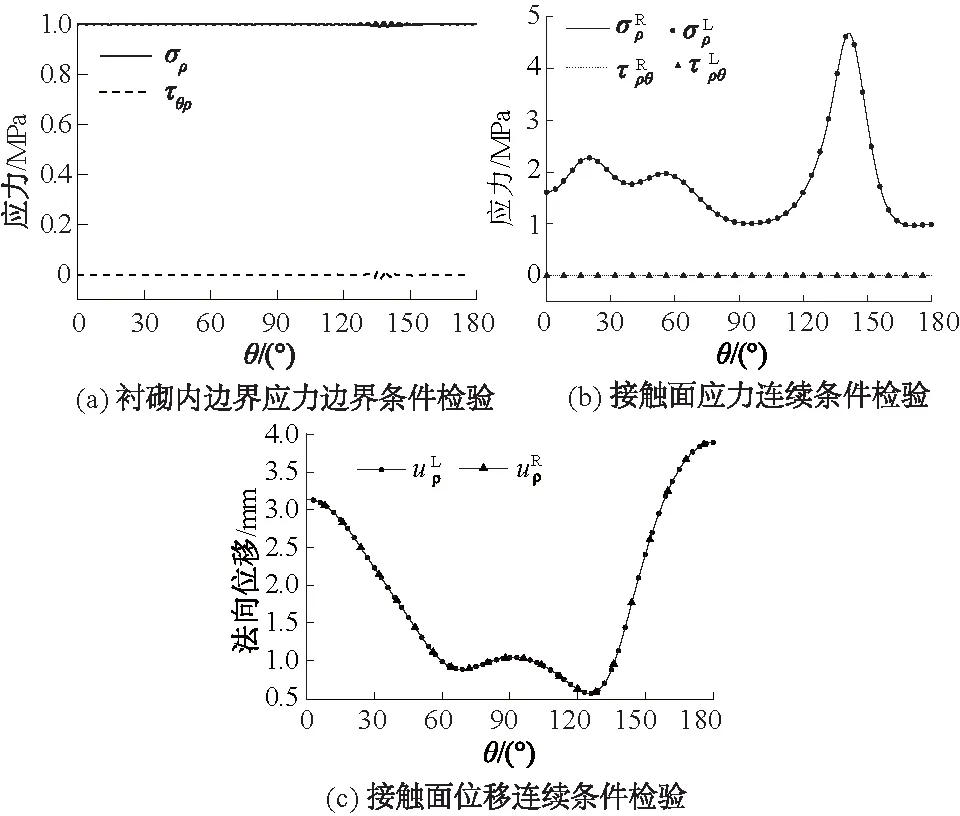
图2 计算精度检验结果Fig.2 Verification of calculation accuracy
同时,为了验证所得结果的正确性,本文应用ANSYS有限元软件对该问题进行了求解。在计算过程中,利用PLANE42单元模拟围岩和衬砌单元。同时,依靠ANSYS软件中的“面—面”接触方式实现围岩和衬砌的接触,将衬砌表面通过网格划分分裂成目标单元TARGE169,并与围岩表面的接触单元CONTA171共享同一个实常数号形成一组接触对,由于本文求解的是完全光滑的接触问题,在关键字选项KEYOPT(12)中应选择2表示允许有相对滑动,且设置2种材料的摩擦系数为0。
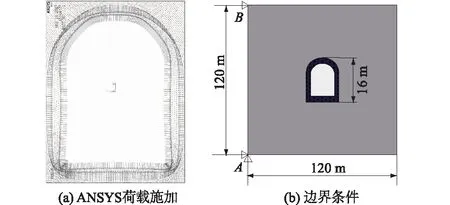
图3 ANSYS荷载施加及边界条件示意图Fig.3 Schematic diagram of load application and boundary conditions in ANSYS
为了考虑时间效应来模拟支护滞后的过程,本文将采用由Dancan等提出的“反转应力释放法”,假设己知荷载释放系数,通过公式与初始条件计算求得开挖后的等效节点荷载[17],根据释放荷载的大小来模拟支护滞后过程,在弹性状态下,位移释放系数与应力释放系数呈线性关系。假设当位移释放了0.2倍的完全自由位移后施加衬砌约束围岩变形,则可知等效释放荷载也相应的释放了0.2倍荷载值,剩余0.8倍荷载作用在衬砌上使衬砌与围岩发生相互作用。而围岩开挖边界的最终应力则需要依靠再叠加初始的原始应力及释放0.2倍等效荷载时对围岩产生的应力进行计算。
如图3所示,所取的模型外边界为120 m,开挖的直墙半圆拱隧洞高为16 m,在A点施加x和y方向的点约束,在B点施加x方向的点约束,在衬砌内边界施加1 MPa的面荷载,计算出的等效节点荷载加载在接触面的节点上。
所得数值解结果和解析解的对比如图4所示。从图4可以得出,衬砌内外边界、围岩开挖边界的切向应力以及接触面上的法向应力的数值解和解析解结果几乎完全相等,证明了本文所得结果的正确性。
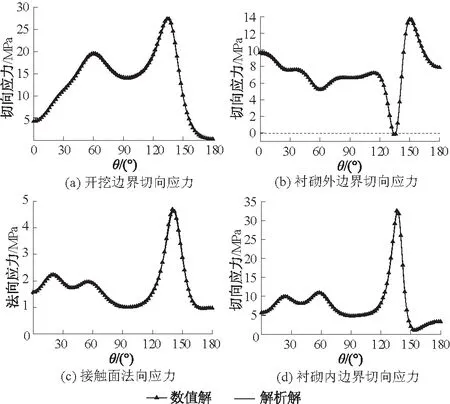
图4 数值解和解析解对比Fig.4 Comparison between numerical andanalytical solutions
4.2 衬砌和围岩应力的讨论
考虑不同参数对衬砌和围岩应力变化的影响,本文选取不同的侧压力系数,不同的位移释放系数以及不同的内水压力进行计算,并对结果进行了分析。首先选取一组不同的侧压力系数λ=0.5,1.0,1.5,2.0,η=0.2,其余参数不变化,所得到的结果如图5所示。
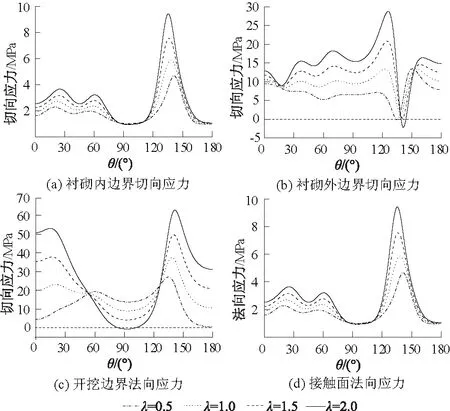
图5 不同侧压力系数下隧洞各边界应力分布(η=0.2)Fig.5 Stress distribution along the boundaries under different lateral pressures λ(η=0.2)
由图5我们可以看出:①直墙半圆拱形隧洞衬砌内外边界和开挖边界上的切向应力以及接触面上的法向应力都在隧洞底部的拐角附近达到最大值;②当λ=2.0时,衬砌外边界的切向应力在拐角处出现了拉应力,开挖边界切向应力在侧墙处出现了较小的拉应力;③衬砌内边界的切向应力和接触面上的径向应力基本随着λ的增大而逐渐增大;④衬砌内外边界的切向应力随着λ的增大,变化趋势越来越显著;⑤衬砌内边界的切向应力和接触面上的法向应力在侧墙处变化较小,而在拐角处变化较大;衬砌外边界的应力在侧墙处变化较大,在拐角处变化较小。
再考虑不同的位移释放系数对应力变化的影响,取η=0.2,0.4,0.6,0.8,λ=0.5,其余参数不变,得到的结果如图6所示。
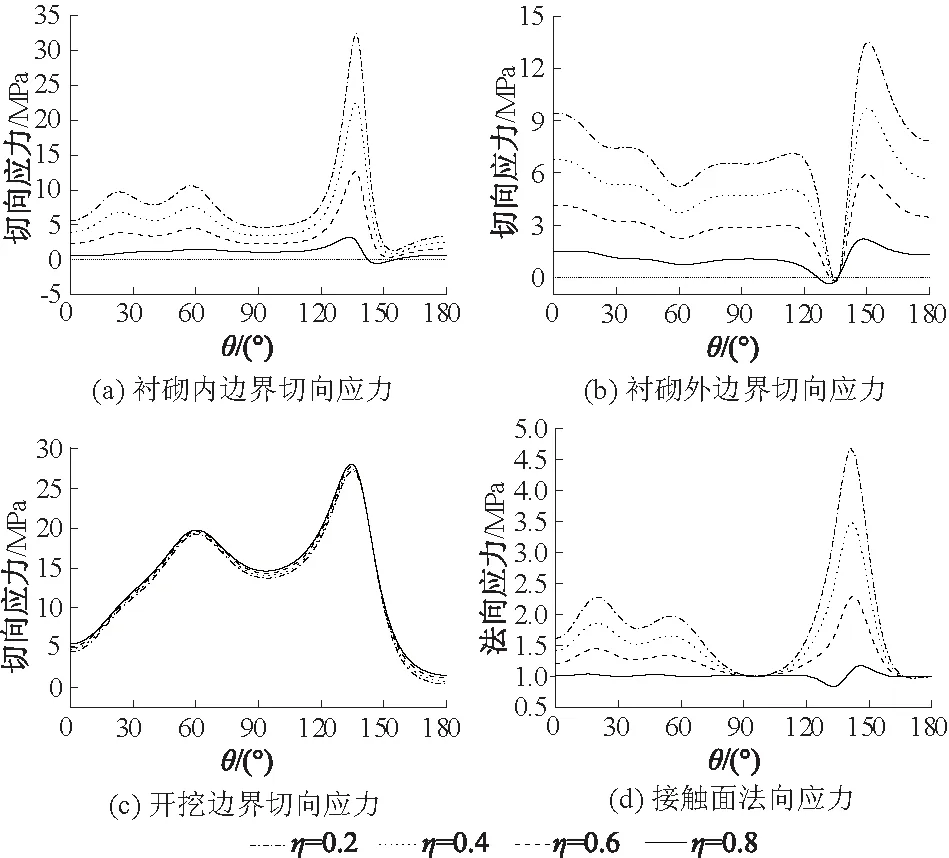
图6 不同位移释放系数下隧洞各边界应力分布(λ=0.5)Fig.6 Stress distribution along the boundaries under different values of displacement release coefficient
由图6我们可以看出:①同样是在直墙半圆拱形隧洞的底部拐角附近出现应力集中;②随着位移释放系数的增大,衬砌内外边界上的切向应力和接触面上的法向应力都变小,而开挖边界上的切向应力变化不大;③衬砌外边界在拐角附近的切向应力为拉应力;当η=0.8时,衬砌内边界的切向应力也为拉应力。
最后,取不同的内水压力Ps=1.0,2.0,3.0,4.0 MPa,侧压力系数λ=0.5,位移释放系数η=0.2,其余参数不变,得到围岩和衬砌的应力如图7所示。
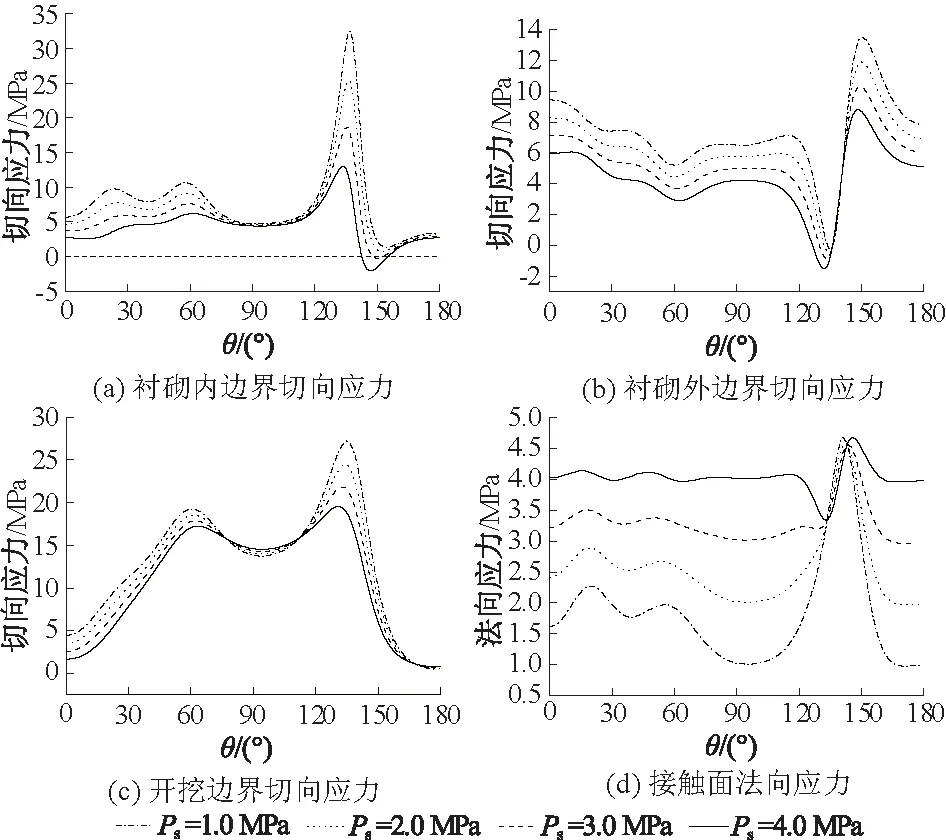
图7 不同内水压力下隧洞各边界应力分布(λ=0.5,η=0.2)Fig.7 Stress distribution along the boundaries under different values of internal water pressure(λ=0.5,η=0.2)
由图7可以看出:①衬砌内外边界和开挖边界上的切向应力随着内水压力的增加而逐渐减小,而接触面上法向应力随着内水压力的增加而逐渐增加;②衬砌内边界和开挖边界的切向应力在拐角附近变化较大,在侧墙处变化较小,而接触面上的法向应力则在拐角附近变化较小,在其他地方变化剧烈;③衬砌外边界在拐角附近出现切向的拉应力,而当内水压力达到3.0 MPa时,衬砌内边界也会出现切向拉应力。
5 结 论
本文利用平面应变假定求解了衬砌与围岩光滑接触且隧洞内作用有内水压力时非圆形水工隧洞的应力和位移解,并且考虑了支护滞后的力学过程。利用幂级数解法求解了直墙半圆拱形隧洞各边界的应力和位移分布,所得结果能很好地满足应力边界条件以及应力和位移的连续条件。通过与ANSYS数值软件所得结果对比,发现当级数的项数达到100项时,数值解和解析解能较好地吻合,证明了该方法和计算过程的正确性。还讨论了不同位移释放系数、侧压力系数和内水压力下围岩与衬砌内的应力分布规律。
(1)衬砌内边界的切向应力和接触面上的法向应力基本随着侧压力系数λ的增大而逐渐增大,侧压力系数过大,会在衬砌边界出现切向的拉应力。
(2)位移释放系数η的增大对开挖边界的切向应力影响不大,衬砌内外边界的切向应力都随着η的增大而减小,η过大会使衬砌内边界出现切向的拉应力。
(3) 随着内水压力的增加,衬砌内外边界和开挖边界上的切向应力而逐渐减小,但是当内水压力>3.0 MPa时,衬砌内外边界的切向应力都为拉应力。由于内水压力的方向是法向的,因此接触面上的法向应力随着内水压力的增大而增大。
(4) 围岩开挖边界的切向应力基本都为压应力,仅有λ=2.0时,在侧墙处出现了很小的拉应力,且都在洞底拐角处出现较大的应力集中。
参考文献:
[1]MUSKHELISHVILI N I. Some Basic Problems of the Mathematical Theory of Elasticity[M]. Leyden:Noordhoff International Publishing, 1977.
[2]吕爱钟,张路青.地下隧洞力学分析的复变函数方法[M].北京:科学出版社,2007.
[3]赵 凯,刘长武,张国良.用弹性力学的复变函数法求解矩形硐室周边应力[J].采矿与安全工程学报,2007,24(3):361-365.
[4]朱大勇,钱七虎,周早生,等.复杂形状洞室围岩应力弹性解析分析[J].岩石力学与工程学报,1999,18(4):402-404.
[5]EXADAKTYLOS G E,STAVROPOULOU M C. A Closed-form Elastic Solution for Stresses and Displacements Around Tunnels[J]. International Journal of Rock Mechanics and Mining Sciences,2002,39(7):905-916.
[6]EXADAKTYLOS G E,LIOLIOS P A,STAVROPOULOU M C. A Semi-analytical Elastic Stress-displacement Solution for Notched Circular Openings in Rocks[J]. International Journal of Solids and Structures,2003,40(5):1165-1187.
[7]WANG M B, LI S C.A Complex Variable Solution for Stress and Displacement Field Around a Lined Circular Tunnel at Great Depth[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009,33(7):939-951.
[8]LU A Z, ZHANG L Q, ZHANG N. Analytic Stress Solutions for a Circular Pressure Tunnel at Pressure and Great Depth Including Support Delay [J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(3):514-19.
[9]LU A Z, ZHANG N, KUANG L.Analytic Solutions of Stress and Displacement for a Non-circular Tunnel at Great Depth Including Support Delay[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 70:69-81.
[10] 吕爱钟,覃 媛,陈虹宇.马蹄形隧洞考虑支护滞后过程的应力分析[J].岩土力学,2014,35(增1):42-48.
[11] LU A Z, ZHANG N, QIN Y.Analytical Solutions for the Stress of a Lined Non-circular Tunnel under Full-slip Contact Conditions[J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 79:183-192.
[12] ZHU W S,LIN S S. Some Practical Cases of Back Analysis of Underground Opening Deformability Concerning Time and Space Effects[C]∥International Society for Rock Mechanics and Rock Engineering, Sixth International Conference on Rock Mechanics, Montreal, Canada, August 30-September 3, 1987. Rotterdam: A.A. Balkema, 1987:1325-1356.
[13] 李云鹏,刘怀恒.典型洞型工作面端部围岩变形特征的有限元分析[J].西安矿业学院学报,1988,8(2):1-8.
[14] 陈子荫.围岩力学分析中的解析方法[M].北京:煤炭工业出版社,1994.
[15] ENGLAND A H, SIH G C. Complex Variable Methods in Elasticity[M]. USA:Wiley-Interscience, 1971.
[16] 吕爱钟.非圆形硐室封闭整体式支护映射函数确定的新方法[J].岩土工程学报,1995,17(4):38-44.
[17] 于学馥.地下工程围岩稳定分析[M].北京:煤炭工业出版社,1983.
