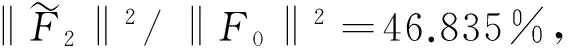关于多因变量综合线性回归的几点注记
2018-05-17刘竹林
徐 伟,孙 涛,刘竹林
(1.南京航空航天大学 经济与管理学院,江苏 南京 211106;2.南京审计大学 国际审计学院,江苏 南京 211815;3.江苏海事职业技术学院 经济管理学院,江苏 南京 211170)
一、引 言
多因变量y1,y2…,yq关于x1,x2,…,xp综合线性回归建模是一个比较成熟的问题,但从近几年很多介绍综合线性回归应用的文章来看[1-6],仍然有不少学者对这类问题的原理存在模糊认识,故本文拟对多因变量综合线性回归的本质与特点作几点解析。

二、三种常用回归建模方法原理解析
(一)OLS法的本质
记
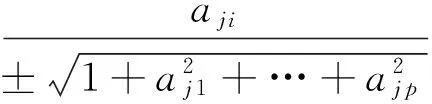
(i=1,2,…,p)
的值最小,作拉格朗日函数:


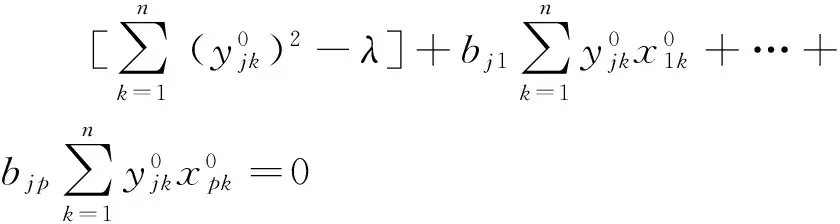

… … …

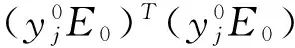

(j=1,2,…,q)
(1)
注意:如果确信自变量中没有多余的,因变量也都几乎独立,可以直接算出(F0E0)T(F0E0)的全部特征值λ1≥λ2≥…≥λp≥λp+1≥…≥λp+q≥0,并且(λp+1+…+λp+q)/(p+q)很小(一般要求<10%),分别令特征向量:

… … …
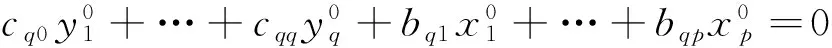
若矩阵[cij]q×q的行列式不为0,则能解出所有因变量的表达式,即得全部回归方程。
(二)PCA法的特点

(三)PLS法简介与本性揭示
众所周知,PLS法计算过程如下:





为了更深刻地理解PLS成分t1,t2,…,tm利用了相关信息的程度,下面来看PLS成分的几个基本性质,并借此对提炼PLS成分的计算过程进行简化。

证明:易见A0是正定或半正定的,A0的全部特征值λ1≥λ2≥…≥λp≥0,记A属于λ1,λ2,…,λp的单位特征向量是α1,δ2,…,δp、C=[α1δ2…δp],从而C是正交矩阵,满足CTA0C=Diag(λ1,λ2,…,λp)[10]141-156,再看:
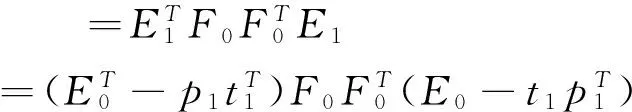



注意到

因此
=Diag(λ1,λ2,…,λp)-λ1[1 0 … 0]T[1 0 … 0]
=Diag(0,λ2,…,λp)
A1正交相似于Diag(λ2,…,λp),从而A1最大特征值λ2对应的单位特征向量可以取α2;同理可证,A2正交相似于Diag(λ3,…,λp),最大特征值λ3对应的单位特征向量可以取α3;如此继续下去,即得性质1,结论成立。
由此性质,PLS法提取PLS成分的过程可简化如下:
1.算出A0的全部特征值λ1,λ2,…,λp,并设(λ1+…+λm)/(λ1+…+λp)≥θ(通常至少取θ>0.8)。


性质3 PLS成分t1,t2,…,tm彼此正交。
证明:
1.对任意取定的1≤i 2.对任意取定的1≤i PLS法用相互线性独立的偏成分t1,t2,…,tm取代原来的p个不完全线性独立的自变量,通常m 下面用一个实例比较几种不同建模方法的回归效果。三次产业产值贡献率(增加值增量与GDP增量之比)是带动就业的一个重要因素,以1998—2011年中国三次产业产值贡献率成分数据为自变量x1,x2,x3,三次产业就业率的成分数据为因变量y1,y2,y3,构建线性回归模型[11]105-106,自变量和因变量的数据标准化见表1。 再返回到原始变量得到: (2) 表1 标准化样本数据表 2.采用PLS法。A,A1的最大特征值对应的单位特征向量分别是: α1=(-0.365 548,-0.633 202,0.682 224)T α2=(0.908 34,-0.402 692,0.112 949)T 两个PLS成分 t1=E0α1=(-0.858 234,-0.441 88,-0.485 564, 0.538 722,0.533 159,-0.226 082,-0.226 255, 0.134 391,0.305 24,0.472 333,0.289 107, 0.145 044)T t2=E1α2=(0.202 835,0.019 356,-0.346 466, 0.177 794,-0.012 281,-0.498 581,0.500 141, 0.156 057,0.015 082,-0.313 212,0.217 703, -0.118 434)T 由于自变量的全体样本点只在一张二维平面内,而直接标准化后仍然在一张二维平面内,所以最多只能有两个PLS成分。进一步算得: F2=F0-t1(-0.838 5,0.434 4,1.002)+ t2(0.019 2,-0.067 8,0.040 3) 再返回到原始变量,得到综合回归方程: (3) E0的信息利用率1-‖E2‖2/‖E0‖2=99%,F0的拟合误差率‖F2‖2/‖F0‖2=69.6%,由式(3)测算出中国2010—2012年三产业就业人数构成情况分别为(%):53.06、18.02、27.52;48.5、19.11、32.32;47.85、19.13、33.04,而中国2010—2012年三产业就业人数构成实际为:41.25、27.04、31.69;40.02、28.41、31.57;33.6、30.29、36.1。 再利用普通最小二乘法,并返回到原始变量得到回归方程: (4) 可以看出,应用案例的拟合效果与测算效果都是OLS法最差、PLS法其次、PCA法最好;但若用1991—2002年全国三次产业产值资料建立回归(具体过程略),结果是PLS法最差、OLS法效果最好;尤其是预测中国2003年、2004年三产业就业人数构成情况分别为:50.61、20.36、29.03;53.6、22.35、24.05,与实际情况49.1、21.6、29.3;46.9、22.5、30.6比较接近。 总之,建立多因变量综合线性回归不存在绝对最好方法,不同资料适合不同方法。若遇到很难从数据资料直接分析出用哪种方法好时,不妨多试验几种方法,并通过比较效果后再确定。评价回归模型的优劣主要看两个标准:第一是总拟合误差小;第二是样本数据信息利用率高。 参考文献: [1] 王惠文,黄薇.成分数据的线性回归模型[J].系统工程,2003(2). [2] 张晓琴,陈佳佳,原静.成分数据的组合预测[J].应用概率统计,2013(3). [3] 姜磊.空间回归模型选择的反思[J].统计信息论坛,2016(10). [4] 詹敏,廖志高,徐玖平.线性无量纲化方法比较研究[J].统计与信息论坛,2016(12). [5] 李玲玉,郭亚军,易平涛.无量纲化方法的选取原则 [J].系统管理学报.2016(6). [6] 林彬.多元线性回归分析及其应用[J].中国科技信息,2010(9). [7] 陈希孺,王松桂.近代回归分析[M].合肥:安徽教育出版社,1987. [8] Wold H.Partial Least Squares[C]∥Kotz S,Johnson N L.cyclopedia of Statistical Sciences,New York:John Wiley & Sons,1985. [9] Quenouille M H.Experiments with Mixtures[J].J.R.Statist.Soc.B,1959(21). [10] 同济大学数学系.线性代数[M].北京:高等教育出版社,2014. [11] 中国统计年鉴(2014)[M].北京:中国统计出版社,2014.


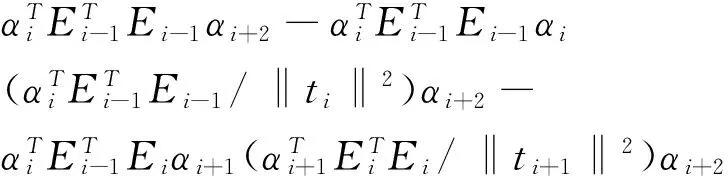
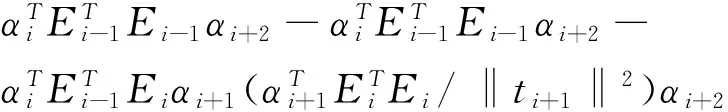
三、几种综合回归建模方法比较