一种基于属性加权的平均单一依赖估计改进算法

秦怀强，赵茂先

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

一、引 言

贝叶斯网(Bayesian Network，BN)也叫做贝叶斯信度网络，它是一个有向非循环图解模型，是概率图解模型的家族成员，它能展示出随机变量间的条件依赖关系[1-2]。然而从一个任意的BN离散变量搜索空间中学习一个最优的BN网络结构是一个NP难问题，因此必须在一定的限制条件下寻找一个最优的BN网络结构[3]。许多学者遵从于这个建议，通过限制BN网络的复杂结构提出了许多合理、有效的算法，如朴素贝叶斯(Naive Bayes，NB)算法，以及在NB算法的基础上进行改进得来的树扩展的朴素贝叶斯(Tree-Augmented Naive Bayes，TAN)算法、平均单一依赖估计(AODE)算法、隐朴素贝叶斯(Hidden Naive Bayes，HNB)算法、加权朴素贝叶斯分类(Weighted Naive Bayesian Classifier， WNBC)算法和消减朴素贝叶斯独立性假设的属性加权(Weighting Attributes to Alleviate Naive Bages Independence Assumption，WANBIA)算法等[4-8]。

NB算法因为它的假设条件(一个实例数据在给定类别属性值的条件下，特征属性值间是相互独立的)，使得它对属性间相关性很弱的数据集进行分类时，效果好速度快。但当这个假设条件被违背时，它的分类效果将会变差。而在现实情况下，数据集中的属性之间大多是有较强相关性的。

AODE算法通过统计的方法，依据训练集中的数据，从测试实例的特征属性值中选出父属性值，将特征属性分为父属性和子属性。它还规定一个测试实例在给定类别属性值和父属性值的条件下，特征属性值间是相互独立的，这极大地消减了NB算法的假设条件。并且AODE算法还是一系列可靠分类模型的聚合，上述这些原因使得AODE算法的分类精确度较NB算法有很大的提高。

在AODE算法的基础上，许多学者又纷纷做出改进。Zheng和Webb提出了一个改进的AODE算法，称为惰性消除(Lazy Elimation，LE)的AODE算法[9]，该算法可以删除掉训练集中的无用数据，从而提高AODE算法的分类精确率。Jiang 和Zhang提出了加权平均单一依赖估计(Weightily Averaged One Dependence Estimators，WAODE)算法[10]。该算法利用互信息计算父属性和类别属性间的关联程度，并将计算结果作为权重对父属性加权。Zhong和Kang也提出了一种WAODE算法，但该算法是利用条件互信息计算在类别属性的条件下父属性和子属性间的关联程度，并将计算结果作为权重对父属性加权。

一般AODE算法将所有的特征属性对分类的贡献程度看成是一样的，在处理一些实际问题时，这样会极大地限制它的分类效果，而上述AODE的改进算法通常采取某种方法来衡量特征属性和类别属性的相关程度，并构造相应的加权公式对特征属性加权。

相关系数Tau-y和Lambda-y可以衡量一个特征属性与类别属性的相关程度[11]，它们的计算值表示以某一个特征属性预测或解释类别属性时可以消减的预测误差值。因此，可以用Tau-y和Lambda-y衡量一个特征属性对分类的贡献程度，它们针对一个特征属性和类别属性的计算值越大，说明该特征属性对分类的贡献程度越大。利用相关系数Tau-y和Lambda-y，依据训练集中的数据，计算所有特征属性对分类的贡献程度，并把相应的结果作为父属性的权值，得到了两个改进的AODE算法：T-AODE和L-AODE算法，然后通过实验验证了这两个算法的分类精确度相较于AODE算法有明显的提高。

二、NB算法和AODE算法介绍

(一)NB算法

在处理分类问题时，给定一个训练数据集D={X(1)，X(2)，…，X(t)}包含t个实例，每一个实例X=(a1，a2，…，an)∈D(它是一个n维的向量，有n个特征属性值)，并且每一个实例都被一个类别属性值y∈Y所标记。在给定X的条件下计算y的后验概率，依据贝叶斯理论可以得到式(1)：

(1)

为了能更加简单地计算似然函数p(X|y)，依据贝叶斯理论的假设条件，可以得到式(2)：

(2)

然后，依据上述的理论就可以得到朴素贝叶斯分类器的构建公式，其具体的形式如式(3)所示：

(3)

(二)AODE算法

AODE算法是结构扩展后的NB算法，它消减了NB算法的假设条件，其具体的描述如下。

给定一个测试实例X=(a1，a2，…，an)，并且X∈D，因为特征属性值ai∈X，所以可以得到式(4)：

p(y，X)=p(y，ai，X)=p(y，ai)p(X|y，ai)

(4)

结合式(1)和(4)可以得到式(5)：

∝p(y，ai)p(X|y，ai)

(5)

基于式(5)和条件独立性假设，可以得到式(6)，并且在式(6)中ai，aj∈X。

(6)

结合上面的理论可以得到AODE算法构建分类器的公式如式(7)所示：

(7)

在式(7)中，F(ai)表示在训练集中特征属性值为ai的训练实例的数目，g为限制条件(取值一般为30)[5]。

三、相关系数加权的AODE算法

在这里我们用相关系数Tau-y和Lambda-y计算训练集中的特征属性对分类的贡献程度，并把计算结果作为父属性的权重，与原有的AODE算法相结合，得到了两个改进的AODE算法：T-AODE和L-AODE算法。

(一)T-AODE算法

在利用相关系数Tau-y对父属性进行加权时，首先，用Tau-y计算每一个特征属性对分类的贡献程度，其具体公式如式(8)～(11)所示：

(8)

(9)

式(8)表示的是在不知道第i个特征属性的情况下预测类别属性时的全部误差。其中，t指的是训练集中训练实例的数目，而式(9)中fiy指的是训练集中第i个特征属性的某一个属性值与类别值y同时出现的训练实例的数目，Ai表示第i个特征属性。

(10)

(11)

式(10)表示的是在知道第i个特征属性的情况下预测类别属性时的误差。

然后结合式(8)和式(10)就可以得到第i个特征属性的权值wi，其具体公式如式(12)所示：

(12)

式(12)表示的是以第i个特征属性预测类别属性时能消减的误差数。结合式(12)和式(7)可以得到T-AODE算法构建的分类器模型，具体形式如式(13)所示：

(13)

(二)L-AODE算法

利用相关系数Lambda-y计算第i个特征属性的权重的公式如式(14)～(16)所示：

(14)

(15)

(16)

式(14)表示的是以第i个特征属性预测类别属性时能消减的误差数。结合式(14)和式(7)可以得到L-AODE算法构建的分类器模型，如式(17)所示：

(17)

(三)T-AODE和L-AODE算法步骤

结合上文内容，这里给出T-AODE和L-AODE算法步骤如表1所示。它们的算法步骤基本是相同的，不同之处只是特征属性权重wi的计算公式，其分别为式(12)和式(14)。

表1 T-AODE和L-AODE算法步骤

四、实验分析

这里将对T-AODE、L-AODE、AODE和NB算法进行数值分类实验。实验使用的数据是UCI标准数据集，数据集的具体描述如表2所示[12]。在实验前需要对数据做如下的预处理。

表2 训练集数据描述

(一)补充缺失的特征属性值

使用weka中的无监督过滤器Replace Missing Values对特征属性的缺失值进行补充。Replace Missing Values使用从训练集中获得的模型或均值补充缺失的特征属性值。

(二)离散化数值型特征属性值

利用weka中的无监督过滤器Discretization离散化数值型的特征属性值，实验时使用的参数是10-bin。

(三)将无用的特征属性删除

如果一个特征属性的某一种属性值的数目几乎就和训练集中的训练实例的数目相等，这说明该特征属性对分类几乎没有贡献，可以使用weka中的无监督过滤器Remove将这种特征属性删除。

(四)去除类别值缺失的训练实例

使用weka中Instances类下的方法delete With Missing Class，将训练集中类别值缺失的训练实例删除。

为了使实验能够进行，需要计算概率p(y)、P(ai|y)、p(y，ai)和p(aj|y，ai)，并且为了避免零概率估计对实验的影响，采用拉普拉斯估计对上述的概率公式进行估计，其具体的公式如下：

(18)

(19)

(20)

(21)

在上述公式中，F(y)指的是训练集中类别值为y的训练实例的数目，F(aj，y)指的是训练集中类别值y和特征属性值aj同时出现的训练实例的数目，F(aj，y，ai)指的是训练集中类别值为y和特征属性值ai、aj同时出现的训练实例的数目，c(Y)指的是类别值的种类数，c(Aj)指的是特征属性Aj的属性值的种类数。

实验采用的是十折交叉验证的方式，所谓的十折交叉验证指的是将一个原始训练数据集平分成10份，进行10次实验，每一次都将这10份数据中的一份作测试集，其它9份作训练集，最终的结果为这10次实验结果的平均值[13]330-333。经过上述的准备，借助Eclipse和weka中的软件包，最终得到了NB、AODE、T-AODE和L-AODE算法的分类精确度，如表3所示。

表3中的分类精确度的单位为%，由表3可以看出T-AODE和L-AODE算法的平均分类精确度均大于AODE算法和NB算法，而且T-AODE算法是这四个算法中平均分类精确度最高的。然后，对比这四个算法在每一训练集上的表现，可以得到表4。

由表4可以看出T-AODE算法针对于每一个数据集与NB、AODE和L-AODE算法比较分类效果。T-AODE分类效果好的数据集数目多于NB、AODE和L-AODE算法，而L-AODE算法分类效果好的数据集数目也多余NB和AODE算法。综上所述，可以看出T-AODE和L-AODE算法的整体分类效果是优于原始的AODE算法。

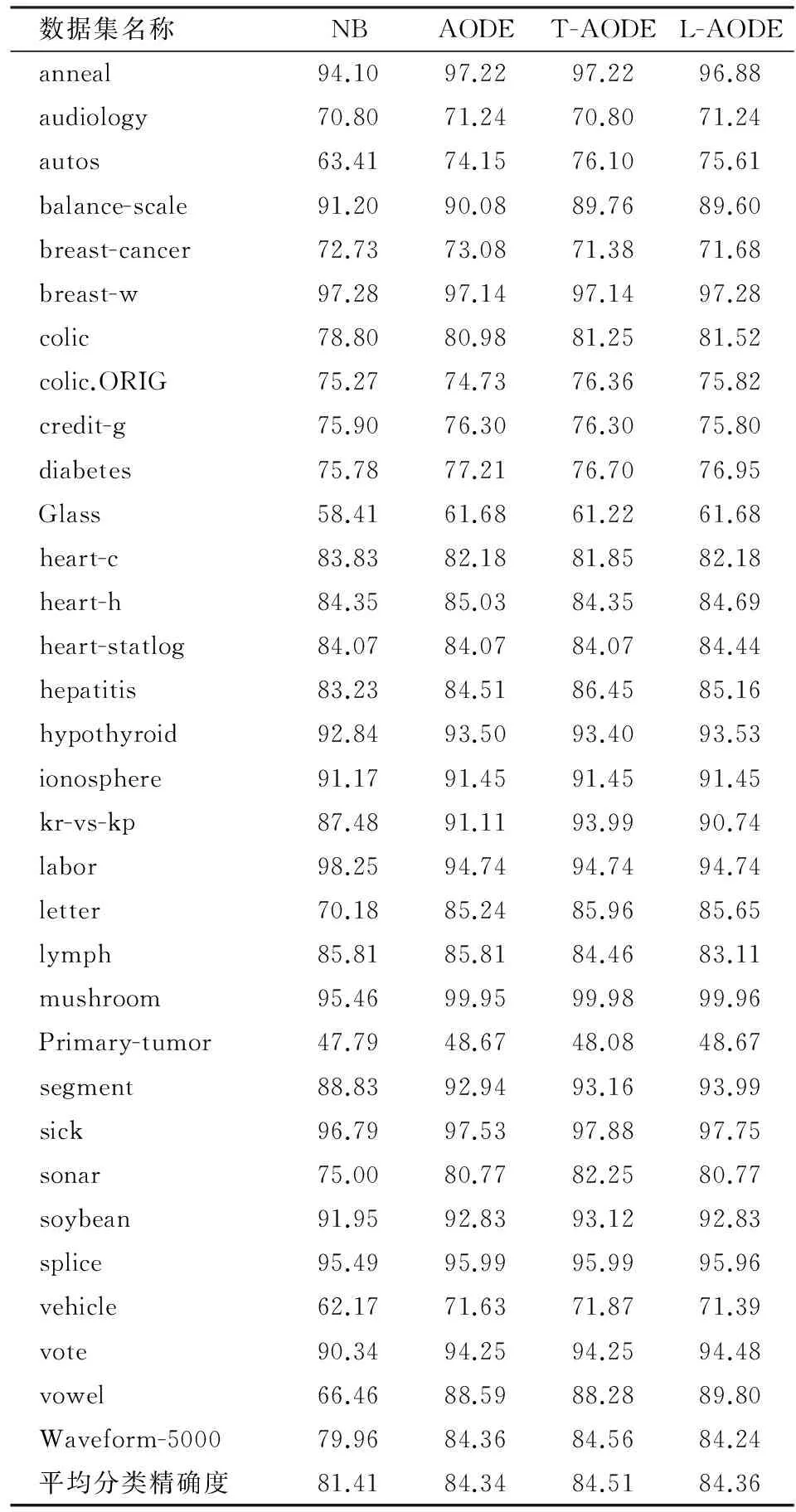
表3 各算法分类精确度对比

表4 各算法在每个数据集上的分类精度对比

五、结束语

本文提出了两个改进的AODE算法:T-AODE和L-AODE算法，它们的核心思想是分别利用相关系数Tau-y和Lambda-y计算各个特征属性对分类的贡献程度，并将得到的结果作为父属性的权值来改进AODE算法。然后通过实验对比了T-AODE、L-AODE、NB和AODE算法的平均分类精确度和在每个数据集上的分类精确度，结果显示T-AODE和L-AODE算法的整体分类效果要优于原始的AODE算法，而且T-AODE算法相较于L-AODE算法效果要更好。

虽然T-AODE和L-AODE算法的整体分类效果都要优于AODE算法，但是二者的加权方式还是过于简单，而且在某些数据集上的分类效果要比AODE算法甚至是NB算法还差，所以在以后的研究中，要探究用更加有效的加权方式改进AODE算法，使得改进算法在每个数据集上的分类效果都要优于原始AODE算法。为此可以考虑利用某种技术计算多个属性混合在一起对于分类的贡献程度，并将计算结果作为特征属性的权值。

参考文献：

[1] Zhong L X，Daeki K.Attribute Weighting for Averaged One-dependence Estimators[J].Applied Intelligence，2017，46(3).

[2] Wu J，Cai Z H，Pan S R，et al.Attribute Weighting：How and When Does It Work for Bayesian Network Classification[C].2014 International Joint Conference on Neural Networks，2014.

[3] Gregory F Cooper. The Computational Complexity of Probabilistic Inference Using Bayesian Belief Networks [J].Artificial Intelligence，1990，42(2/3).

[4] Friedman N，Geiger D，Goldszmidt M.Bayesian Network Classifiers[J].Machine Learning，1997，29(2/3).

[5] Geoffrey I W，Janice R B，Wang Z H.Not So Naive Bayes：Aggregating One-dependence Estimators[J].Machine Learning，2005，58(1).

[6] Jiang L X，Zhang H，Cai Z H.A Novel Bayes Model:Hidden Naive Bayes[C].IEEE，Transactions on Knowledge and Data Engineering，2009，21(10).

[7] Hamad A.Weighted Naive Bayesian Classifier[C].IEEE International Conference on Computer Systems and Application，2007.

[8] Nayyar A，Zaidi，Jesus C，et al.Alleviating Naive Bayes Attribute Independence Assumption by Attribute Weighting[J].Journal of Machine Learning Research，2013，14(1).

[9] Zheng F，Webb G I.Efficient Lazy Elimination for Averaged One-dependence Estimators[C].Proceeding of the 23rd International Conference on Machine Learning，2006.

[10] Jiang L X，Zhang H.Weightily Averaged One-dependence Estimators[C].The 9thPacific Rim International Conference on Artificial Intelligence，2006.

[11] 喻凯西.朴素贝叶斯分类算法的改进及其应用[D].北京：北京林业大学，2016.

[12] Merz C，Murphy P，Aha D.UCI Repository of Machine Learning Database[DS/OL].Dept.of ICS，Univ.of California，http://www.ics.uci.edu/mlearn/MLRep-ository.html，1997.

[13] 袁梅宇.数据挖掘与机器学习WEKA应用技术与实践[M].北京：清华大学出版社，2014.