基于混沌PSO优化BP神经网络的碳价预测

2018-05-17彭紫君

统计与信息论坛 2018年5期

蒋锋，彭紫君

(中南财经政法大学统计与数学学院，湖北武汉 430073)

一、引言

近年来，全球气候变暖、雾霾污染及二氧化碳排放过量等环境问题日益严峻，为控制温室气体排放，欧盟建立了第一个碳排放交易体系(EUETS)，其标的产品是欧盟排放配额(EUA)。有履约责任的成员国需要向欧盟提交本国的减排方案，这些方案中会详细提及企业能够排放的温室气体上限。如果实际碳排放超过上限，则企业需要为超过的部分缴纳一定罚款，或向碳排放量有结余的企业来购买碳排放配额，由此形成了碳市场，而这些交易的价格就构成了EUA价格。EUA价格是评价碳市场体系有效性的核心要素，它不仅是调剂供需的重要工具，还是碳金融衍生品发展的关键因素。

在EUETS体系下，世界各地多个碳交易所逐渐兴起。中国自2013年起相继在7个城市启动了碳排放权交易试点，研究基于多影响因素的国际碳市场价格预测，并为中国碳市场价格研究提供新的方法，这样不仅可以为个人投资者对碳市场的参与提供潜在的风险机理，还可以为企业投资者开发中国核准减排项目提供技术支持。

国外对于碳价预测的研究起步较早，按照研究主体方法可分为参数方法与非参数方法。有学者运用参数方法进行碳价预测，如Paolella和Taschini利用GARCH 模型对碳市场价格进行预测，研究发现预测值与实际值较为接近[1]；Byun和Cho将电价、原油价格影响因素纳入模型设计中，运用GARCH模型对EUA期货价格波动率进行预测[2]。在此基础上，学者们开始引入非线性方法来处理碳市场价格的非线性波动，如Zhu 和Wei提出了ARIMA-LSSVM模型，对欧盟气候交易所的碳期货合约进行了建模与实证[3]；王娜采用Boosting算法进行最优子集的寻找，有效解决了ARMA模型的识别问题，并对碳价进行了准确预测[4]。

考虑到神经网络在处理复杂非线性问题的优势，Tsai 和 Kuo采用RBF神经网络将煤炭、石油、天然气价格作为输入变量对欧盟市场碳价进行预测，研究表明RBF神经网络模型能较好预测碳价波动[5]。年敏考虑到碳市场CER现货价格不仅受到能源价格影响，还会受到宏观经济、同类替代品价格等影响，采用了BP 神经网络模型对核准减排量(CER)价格进行预测，研究表明加入碳价影响因素能增强模型的预测能力[6]；张晨和胡贝贝运用EEMD分解BP神经网络预测的误差序列，结果表明误差校正能提升多因素国际碳市场价格的预测效果[7]。此外，还有学者采用群体智能算法对神经网络碳价预测模型进行优化，如朱帮助和魏一鸣运用数据分组处理法(GMDH)选择对当期碳价最有影响的滞后期价格，并且运用粒子群算法(PSO)进行优化[8]。

国内外对经济、金融时间序列的预测越来越关注于对高维数据的降维方法，碳价预测的变量选择也不例外。Guobrandsdóttir等通过相关性分析对欧盟碳价影响因素进行降维，并对EUA 碳价进行了多元线性回归分析预测[9]；朱帮助针对碳价影响因素之间的多重共线性分析得到了稳健的回归结果，运用岭回归方法得出 EU ETS碳期货均衡市场价格模型，并分析得出实际值与均衡价格之间差异的原因可能是受到能源价格波动、市场预期、第一阶段配额在第二阶段不再适用以及欧债危机的影响等[10]；还有学者用最小绝对值收缩选择(LASSO)方法对高维网络大数据进行变量选择，并结合网络结构自回归分布滞后模型对中国碳价进行了预测，结果表明LASSO的优化显著提升了碳价的预测能力。

综上所述，现有文献中的碳价预测模型大多也未对高维变量降维，这将使预测模型冗杂且不稳定；而运用人工神经网络大多未考虑初始权值阈值的选取，使得模型极易陷入局部最小值。笔者基于上述两点，提出基于多维影响因素的碳价预测模型：引入Elastic Net方法筛选出碳价的主要影响因素，对BP神经网络的输入变量进行有效降维；运用混沌粒子群(CPSO)算法对神经网络的初始权值和阈值进行迭代寻优，构造CPSO-BP碳价预测模型；将该算法与BP神经网络、普通粒子群优化的BP神经网络(PSO-BP)和果蝇算法优化的神经网络(FOA-BP)相比，显示出其收敛速度和精度上的优越性。

二、碳价预测模型

(一)Elastic Net碳价影响因素选择

目前，关于碳价预测的研究在变量降维上主要采用最小绝对值收缩选择(LASSO)方法，或改进的自适应LASSO方法和岭回归方法。此类方法存在的共有缺陷是：在超高维或存在强相关的多维变量组时，二者都只能随机地从变量组中选取一个变量。

本文在已有研究的基础上采用弹性网(Elastic Net)方法进行变量选择[11]。与以上两种方法类似，其主要思想是在系数约束的条件下使对数似然函数最大化，以便出现一些取值为0的回归系数，从而得到系数的估计值，而这一思想主要通过加入正则惩罚项得以实现[12]，并以线性模型为例，将其定义为：

=arg min{‖y-Xβ‖2+λ1‖β‖1+λ2‖β‖2}

(1)

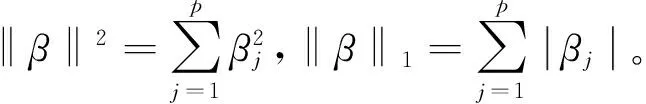
(二)粒子群算法及其改进

PSO算法是仿照鸟群觅食的生物智能方法[13]。在此算法中，每一只“鸟”相当于算法中进行搜索的一个“粒子”，将问题的最优解看作是鸟群搜寻的“食物”。假定每个粒子都已知到目前为止自己的最好位置(Pbest)和所有粒子发现的最好位置(Gbest)，那么在每一次搜寻食物的过程中，粒子都可以通过Pbest和Gbest来更新自己的速度和位置。

假设待解决的优化问题是一个N维向量，第i个粒子的位置和速度可表示为：

xi=(xi1,xi2,…,xiN)T

ui=(ui1,ui2,…,uiN)T

计算得到Pbest和Gbest后，粒子即可根据式(2)式(3)来更新自己的状态：

(2)

(3)

其中k为当前迭代次数；d为解空间的维数；i为种群数目；c1、c2和w为权重系数；rand1和rand2为介于[0,1]之间的随机数。

在PSO中，每一个粒子通过Pbest和Gbest来更新自己的位置和速度。在一次搜索中，如果有一个粒子落入局部最优，其他粒子会迅速地聚集在其身边，导致算法过早收敛，即为“早熟”。为了克服PSO算法“早熟”的缺陷，使粒子群搜索更为广阔的区域，本文构造了一个混沌映射对Gbest进行混沌扰动。考虑到Logistic映射计算量小，本文用Logistic方程构造混沌映射，具体做法是利用Logistic混沌映射使当前产生的序列Gbest生成一个新的序列，再用新序列中Pbest最优的粒子替换某个粒子的位置，从而搜寻全局最优解。

(三)基于CPSO优化的BP神经网络模型

BP神经网络模型是目前技术最成熟的神经网络模型，该模型可通过对历史数据的学习自主寻找出参数之间的规律。由于碳排放权交易的历史价格及其影响因素呈现着明显的非线性特征，因此本文将BP神经网络作为碳价预测的基本方法。传统的BP神经网络学习过程的本质是权值和阈值的更新，因而可以通过CPSO算法的迭代寻优来训练BP神经网络的权值和阈值，使训练误差尽可能低。本文用CPSO算法中粒子位置来对应模型的权值和阈值，以模型的均方根误差作为算法的适应度函数，迭代找出适应度函数最优值，再根据CPSO算法得到的权值阈值来训练网络得到最终输出结果。

本文构造的基于Elastic net变量选择的CPSO-BP模型的具体流程如下：通过Elastic Net方法选择碳价的影响因素，并将碳价影响因素作为神经网络的输入；确立BP神经网络的拓扑结构以及CPSO算法的初始参数；以BP神经网络的均方根误差RMSE作为CPSO算法的适应度函数进行迭代寻优，并对整个粒子群的最优位置进行混沌优化，具体做法是：用混沌映射得到的序列中适应度函数值最低的粒子的位置代替任意一个粒子的位置；当算法达到最大迭代次数时终止算法，并将输出结果作为BP神经网络的初始权值和阈值进行训练。综上，本文构建的CPSO-BP碳价预测模型流程见图1。

图1 CPSO-BP模型结构图

三、实证分析

(一)指标选择与数据预处理

本文选取欧洲能源交易所公布的2016年12月到期的EUA期货价格，作为研究主体。对于代表各类影响因素的样本指标，本文分别从配额供给、能源价格、宏观经济和碳市场相关产品价格四大维度进行选取。具体而言，在碳价的影响因素中：采用每日成交量反映EUA供给；采用电力价格、煤炭价格、石油价格和天然气价格反映能源价格因素；采用EUA现货价格、CER期货价格、历史价格和现货价格反映碳市场相关产品的价格波动对EUA的影响；采用欧洲Stoxx50指数反映宏观经济景气指数对碳价波动的影响，其代表变量见表1。

表1 碳价影响因素的代表变量及其数据来源表

考虑到EU ETS减排计划的三个阶段中，在第一、第二调整阶段，欧盟碳价剧烈波动以致难以预测；而自第三阶段起碳市场日趋成熟，由机制调整导致的价格大幅波动较少，能够更为客观地反映市场运行机制。因此，本文的研究样本将第三阶段即2013年作为研究起点，选取的研究样本为2013年1月4日至2016年9月1日欧洲能源交易所公布的EUA期货价格。在剔除EUA期货价格及其影响因素数据的缺失值后，选取公共的时间区间，最终得到了866组交易日的样本数据。

(二)碳价影响因素的筛选

运用 Elastic Net方法对碳价影响因素进行变量选择。在进行降维前先对原始数据进行归一化处理，以消除指标量纲的影响。本文运用Elastic Net方法，结合AIC准则，给出了变量选择结果及参数估计值，见表2。

表2 碳价影响因素的参数估计结果表

由表2可知：EUA0、CER1、CER2、STO、OIL、COAL对EUA期货价格有正向影响；GAS对EUA期货价格有负向影响；VOL、EPR1、CER0对EUA期货价格影响不显著；CER滞后期现货价格对 EUA期货价格影响不显著，可能是由于碳市场存在多个碳排放权交易品种，还有国际排放贸易机制(ET)的配额AAU可以作为EUA替代产品，由于企业产生排放权交易需求时会在其中进行选择，因此导致 CER对EUA的替代作用并不明显；电力价格对EUA期货价格影响不显著，可能是由于政府对电力价格的强有力监管造成的[14]。

(三)CPSO-BP碳价预测与分析

1.模型网络结构设计。根据Elastic Net方法对碳价影响因素的降维可知，CER 期货价格、EUA现货价格、宏观经济活动、煤炭价格、原油价格和英国天然气价格与碳价的影响程度较大，经过输入变量的不断调节，选取了拟合结果较优的三个节点作为神经网络的输入，即煤炭价格、石油价格和天然气价格；BP神经网络的隐含层为三个节点，BP神经网络的输出层为一个节点，即EUA期货价格。

2.CPSO算法参数选取。

粒子数m：本文取粒子数目为40。

维数N：在本文中，PSO算法解空间的维数是BP神经网络权值与阈值的和。

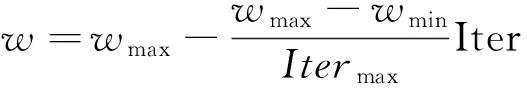
加速常数c1和c2：权衡自己和社会经验所起作用的重要程度，本文取c1=c2=2.41。

最大飞行速度Vmax：防止由于速度过大而忽略最优目标值，本文设定Vmax为0.6。

3.模型拟合结果。利用Elastic Net方法得到的主要影响因素对应的866条数据来进行训练和测试。为验证模型的稳定性和泛化能力，以不同比例多次划分训练集和测试集，结果表明新方法在不同的测试集上都具有良好的表现。将数据以4∶1的比例划分为训练集和测试集，划分训练集为前716天的数据，测试集为后150天的数据。样本外(测试集)数据的拟合结果与相对误差分别见图2图3。

图2 CPSO-BP碳价预测模型拟合结果图

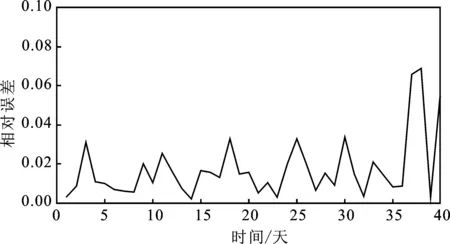
图3 CPSO-BP碳价预测模型相对误差图

由图2可知：CPSO-BP模型可准确地预测碳价变化的总体涨跌趋势，但同时可看到在碳价涨跌幅度较大的部分，其预测值存在着一定的滞后性，与实际值有一定差距，这通常是由一些影响碳价波动的政策性事件或一些突发性事件造成的，并且这种事件一般是无法预料到的，比如像极端气候现象和小型的金融危机等；由图3可知：CPSO-BP碳价预测模型的相对误差十分稳定，且相对误差最高不超过0.1，大部分维持在0.08以下，由此可见CPSO-BP网络模型的辨识精度较高，并且模型较为稳定。

4.模型的对比分析与讨论。本文运用均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)对BP、FOA-BP、PSO-BP以及CPSO-BP模型进行综合评价，三个指标的计算公式依次为：

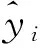
为了对CPSO-BP碳价预测模型的性能进行检验，本文分别采用BP神经网络、FOA-BP模型、PSO-BP模型以及CPSO-BP模型进行模拟和误差分析，并与CPSO-BP相比较。四种神经网络模型的拟合结果见图4所示，四种神经网络模型的相对误差见图5所示，样本外(测试集)的误差分析结果见表3所示。

图4 四种神经网络模型拟合结果图

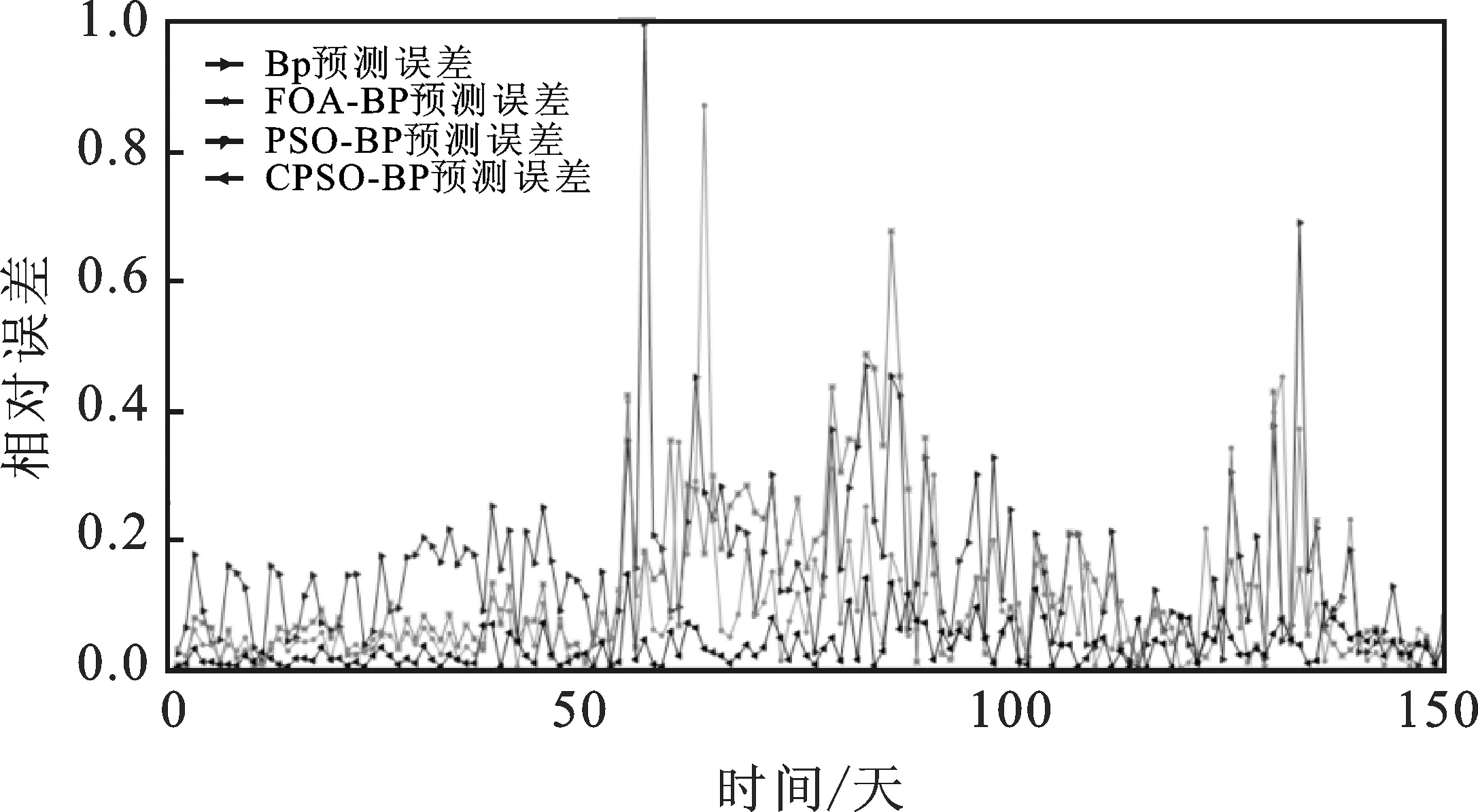
图5 四种神经网络模型相对误差图

由图4可知：CPSO-BP模型的拟合效果最佳，其次分别是PSO-BP与FOA-BP，而传统BP神经网络对碳价的拟合效果是最差的，说明CPSO算法对BP神经网络的局部寻优特性和PSO算法的“早熟”特性进行了一定程度的改进。由图5可知：相比传统BP神经网络，PSO-BP、FOA-BP和CPSO-BP神经网络模型得到的相对误差更低且较稳定，相对误差最高不超过0.1，大部分维持在0.08以下。因此，CPSO-BP算法得到的精度更高，与实际结果更为吻合。

根据图3的CPSO-BP碳价预测模型相对误差和图5的四种神经网络模型相对误差，可以发现CPSO-BP的相对误差一直稳定维持在0.08以下，波动幅度极小，且均在正常范围内波动；而传统BP神经网络、PSO-BP与FOA-BP的拟合效果极不稳定，其相对误差的涨跌幅度极大，均大于0.6；拟合结果最不稳定的是传统BP神经网络模型，误差最高的一个样本点相对误差达到了1，可见优化算法可以减弱传统BP神经网络初始权值阈值设定的随机性，在一定程度上提高了模型的稳定性，而在这三种优化算法中CPSO算法的优化效果最为显著。

表3 四种神经网络模型误差对比表

表3给出了基于一维价格时间序列预测(仅将碳价历史数据作为输入变量)和多维影响因素预测的预测误差。由表3可以看出：将影响因素作为神经网络模型的输入能有效提高碳价预测模型的精度；用CPSO算法对BP神经网络算法的参数进行优化能有效提高模型的精度。具体而言，多影响因素预测中的各项误差均相对低于单价格序列中的各项误差，可见多维影响因素能更好地刻画价格的波动机制；在单价格序列预测和多影响因素预测中，CPSO-BP模型都具有最小的RMSE、MAE和MAPE，而BP模型的预测误差差异较大，这表明CPSO-BP模型能对传统BP模型在稳定性与精确度上进行双重优化。

四、结论

本文利用Elastic Net方法降维，筛选出碳价的主要影响因素，引入CPSO算法优化BP神经网络来预测碳价，显著提高了预测效果，其结论如下：

第一，考虑多种影响因素将提高碳价的预测精度。本文将一维价格序列与多维影响因素序列的预测结果进行对比，结果表明无论用何种神经网络方法，基于多种影响因素的预测将更为精确。

第二，运用Elastic Net可对BP神经网络的输入变量进行有效降维。本文基于Elastic Net方法降低模型复杂度，筛选出了碳价的主要影响因素，为BP神经网络模型输入节点降维提供了有效的路径。

第三，混沌映射克服了传统PSO算法容易“早熟”的弊端。本文构造的CPSO-BP碳价预测模型算法收敛速度快、算法精度高、稳定性强。

碳减排推动了全球碳市场迅速发展，研究及预测国际碳市场价格能够为市场参与者积极参与碳市场提供重要的理论指导。本文的Elastic Net降维方法将对基于大数据的价格预测具有重要的启示意义，运用CPSO-BP模型对碳交易价格进行预测，也能为中国碳价预测提供一种稳定而有效的新方法。然而，由于国内外碳排放权价格中有些因素因数据的可获取性未被纳入本模型中，故本研究仍需对此继续探讨，并随着全国碳排放的快速发展，未来可进一步对中国碳市场进行深入研究。

参考文献：

[1] Paolella M S，Taschini L.An Econometric Analysis of Emission Allowance Prices [J].Journal of Banking and Finance，2008，32(10).

[2] Byun S J，Cho H.Forecasting Carbon Futures Volatility Using GARCH Models with Energy Volatilities [J].Energy Economics，2013，40(2).

[3] Zhu B Z，Wei Y M.CarbonPrice Forecasting with a Novel Hybrid ARIMA and Least Squares Support Vector Machines Methodology [J].Omega，2013，41(3).

[4] 王娜.基于Boosting-ARMA的碳价预测[J].统计与信息论坛，2017(3).

[5] Tsai M T，Kuo Y T.Application of Radial Basis Function Neural Network for Carbon Price Forecasting [J].Applied Mechanics and Materials，2014，590.

[6] 年敏.欧盟核证减排量期货市场有效性研究[D].合肥:合肥工业大学，2015.

[7] 张晨，胡贝贝.基于误差校正的多因素 BP 国际碳市场价格预测[J].价格月刊，2017(1).

[8] 朱帮助，魏一鸣.基于GMDH-PSO-LSSVM的国际碳市场价格预测[J].系统工程理论与实践，2011(12).

[9] Guobrandsdóttir H N， Haraldsson H N. Predicting the Price of EU ETS Carbon Credits [J]. Systems Engineering Procedia，2011(1).

[10] 朱帮助.国际碳市场价格驱动力研究——以欧盟排放交易体系为例[J].北京理工大学学报：社会科学版，2014(3).

[11] 谢合量，胡迪.多因子量化模型在投资组合中的应用——基于LASSO与Elastic Net的比较研究[J].统计与信息论坛，2017(10).