基于模糊回归模型的洪水灾害分级评估方法研究

龚艳冰，向 林，刘高峰

(1.河海大学 水利信息统计与管理研究所，江苏 常州 213022；2.江苏省“世界水谷”与水生态文明协同创新中心，江苏 南京 211100)

一、引 言

分级是指将具有相同特征的一类事物，根据某种特征的程度不同，从高到低(或从低到高)分为不同的级别(或等级)。《国家突发公共事件总体应急预案》将突发公共事件分为四级，即Ⅰ级(特别重大)、Ⅱ级(重大)、Ⅲ级(较大)和Ⅳ级(一般)。由于突发事件的类型不同，各类型的评估指标也不相同，并且相关数据采集困难，因此分级决策仍然主要依靠决策者的直觉和经验来确定。事实上，由于分级本身的模糊不确定性和相关采集数据的不确定性，导致突发事件分级中存在决策主观性和随意性较强，不能客观反映突发事件的级别特征。为了对突发事件进行科学合理分级，急需建立基于不确定数据驱动的客观分级模型，为决策者提供科学依据。目前，国内外学者对突发事件分级评估方法的研究已经有了一定的实践经验和理论成果。例如，商丽媛等采用多分类支持向量机方法对地震突发事件进行了分级[1]；李祚泳等用物元分析方法对自然灾害进行分级研究[2]；吴凤平等提出一种基于三角模糊数改进的灰色定权聚类方法，以三角模糊数表示分级指标的判断信息[3]；宋莎莎和蔡正杰等将模糊层次分析法应用于突发事件分级研究[4-5]；黎育红和张艳琼等将云模型引入分级模型中，较好地解决了突发事件存在的模糊性与随机性[6-7]。

洪水灾害具有突发性、不确定性、多样性、紧迫性和非常规性等特点。对洪水灾害事件进行快速准确的识别，将其划分为不同等级，从而采取相应的应急措施，是应急管理的前提，也是制定应急预案以及资源调配的基础[1]。现有自然灾害分级方法虽然考虑到了分类等级的模糊性问题，但是对于影响分级的指标数据不精确问题考虑的不多。为此，本文提出一种新的基于模糊线性回归模型的洪水灾害分级方法，该方法假定样本指标数据是不精确的，构建样本指标自变量和模糊分类等级因变量之间的模糊线性多元回归模型，通过模糊回归系数反映这种不确定性。本文提出的模糊回归方法利用模糊回归系数来反映各个影响指标因素与分类等级之间的模糊关系，既保留它们之间的因果关系，又反映它们之间的模糊不确定性，从而弥补了决策者经验的主观性，使洪水灾害事件分级结论更加客观合理，为应急管理做出科学指导。

二、基于可能性均值-标准差距离的模糊回归模型研究

(一)基本概念及模糊数距离

定义1 设模糊数A的隶属函数为：

(1)

则称A=(a,α，β)为三角模糊数，其中α，β称为三角模糊数的左右扩展。根据Zadeh的扩展原理，得三角模糊数A=(a,α1，β1)和B=(b,α2，β2)的算术运算法则为：

A+B=(a+b，α1+α2，β1+β2)，

kA=(ka,kα1,kβ1)(k>0)

(2)

定义2 设模糊数A的γ截集为A(γ)=[al(γ)，au(γ)]，则模糊数A的可能性均值和方差分别为[8]：

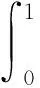
(3)

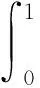
(4)

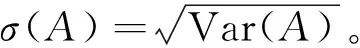
(5)

如果两个三角模糊数A和B相等，当且仅当它们的可能性均值和方差(或标准差)相等，即M(A)=M(B)且Var(A)=Var(B)(或σ(A)=σ(B))，给出可能性均值-标准差距离的概念，即三角模糊数A和B的距离可以定义为：

D(A,B)=

(6)

显然，三角模糊数A和B的可能性均值-标准差距离满足距离测度的非负性、对称性和三角不等式性质，即：

①D(A，B) ≥ 0 且D(A，B) = 0

②D(A，B) =D(B，A)

③D(A，C) ≤D(A，B) +D(B，C)

(二)模糊线性回归模型及参数估计

针对现实世界语言值的模糊性，日本学者Tanaka等人首次提出模糊线性回归模型，主要用于反映自变量和因变量的模糊关系[9]。国内外许多学者对模糊线性回归模型的参数估计方法进行了大量研究，并在系统预测、评估和决策等方面开展了大量应用研究[10-11]。

考虑自变量回归系数和因变量都为模糊数的线性回归模型，即:

yi=y(xi)=b1x1i+b2x2i+…+bpxpi

(i=1,2,…,n)

(7)

其中，bj表示模糊回归系数，yi表示模糊因变量，xji表示实数自变量，一般假定大于0。为方便起见，以三角模糊数为例，并令三角模糊数bj=(kj,αj，βj)(j=1,2,…,p)，则模型(7)可改写成：

yi=(k1,α1，β1)x1i+(k2,α2，β2)x2i+…，+

(kp,αp，βp)xpi

(8)

根据模糊数的运算法则式(2)，上述三角模糊数回归模型等价于：

yi=(ymi,αli,βui)

(9)

为了估计上述模型的参数，为了估计模型(7)或(8)的自变量回归系数，可将模糊因变量估计值与观测值间的误差平方和表示为：

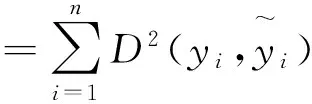
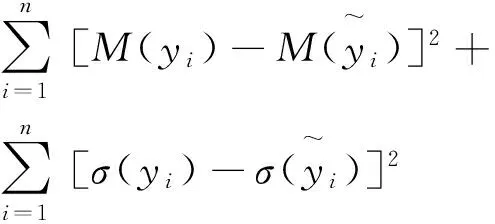
(10)

对于三角模糊数将式(5)代入式(10)，可得误差平方和为：

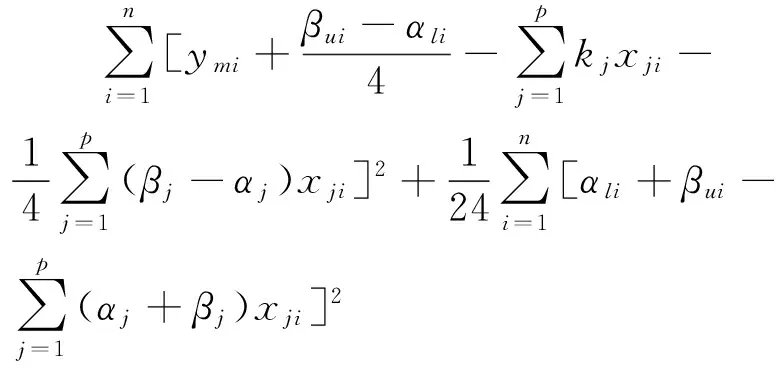
(11)

根据最小二乘原理，对于j=1，2，…，p，上述误差平方和最小，只需令：

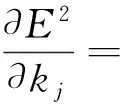
(12)

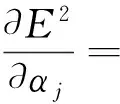
(13)

(14)

记

K=(k1，…,kp)T,α=(α1,…,αp)T,β=(β1，…,βp)T

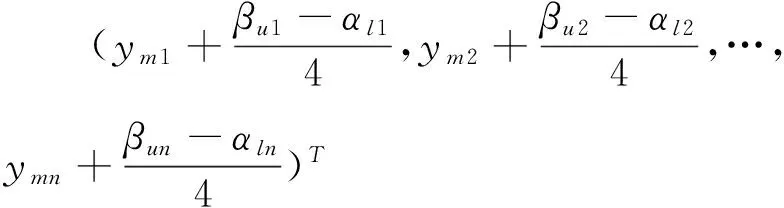
Yv=(βu1+αl1,βu2+αl2,…,βun+αln)T

则等式(12)～(14)可以写成下列矩阵形式：

(15)

通过求解上述线性方程组(15)可得到模糊线性回归模型(7)的回归系数的估计值，我们称这种最小二乘参数估计方法为可能性均值-标准差距离最小二乘方法，简称PMVD-LSM。

三、基于模糊回归模型的自然灾害事件分级评价

自然灾害事件灾情分级评价就是将观测到的灾情样本对象，根据灾情影响指标体系划分为若干个模糊语言等级(如：轻灾、中灾、重灾)的过程。分级评价过程中，需要考虑指标体系的权重和等级的模糊性问题，这也是自然灾害等级评价中的难点。本文将灾情等级和影响因素表示为自变量和因变量的模糊关系并建立模糊回归方程，通过可能性均值-标准差距离最小二乘方法求得模糊回归方程的回归参数估计值，这个参数即为广义权重值。根据历史指标数据，通过模糊回归方法进行客观分级，得到的分级结果是建立在真实不精确数据基础上，从而避免了主观随意性。同时，由于权重值是一个模糊数，因此，可以很好地反映不同专家在进行灾情等级评估中的模糊性和动态性，使得评价结果更符合实际。基于模糊回归模型的灾害事件分级过程如图1所示。

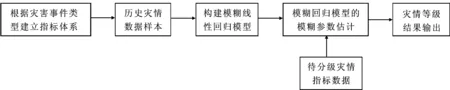
图1自然灾害事件等级评估方法过程图

具体计算步骤如下：

(1)根据灾情事件的类型，分析相关的影响因素，建立m个灾情指标体系；

(2)根据实际情况，假设有s个不同的模糊语言等级(如：轻灾、中灾、重灾)，并将s个等级转化为s个三角模糊数；

(3)根据指标系统中的因素，收集相关的历史灾情数据，构成n个模糊回归样本集(xi，yi)，其中xi表示影响因素(自变量)，yi表示模糊等级(因变量)；

(4)建立灾情分级的模糊回归模型，并利用式(15)求解回归参数的估计值；

(5)将待分级灾情事件的指标数据输入到模糊回归模型中，根据可能性均值-标准差距离公式(6)计算y与s个语言等级之间的距离，选取距离最小的si即为灾情等级结果。

四、应用实例

本文以洪水灾害事件分级为例，验证基于模糊回归模型的灾情等级评估方法的可行性。根据相关文献提供的数据资料，选取中国部分省市1989—1990年间发生的45个洪水灾害的灾情数据作为评估实例，其中包括湖南、山东、安徽、陕西、山西、甘肃、福建、广东、广西、四川等多个地区所发生的暴雨灾情案例，灾情评估指标选取房屋倒塌数量、受灾面积、伤亡人数和直接经济损失[2,6]。本文将前40个为样本训练数据(表1)，后5个作为测试数据(表2)。选取灾情评估指标特征分别为：房屋倒塌数量(x1)、受灾面积(x2)、伤亡人数(x3)和直接经济损失(x4)，用40个训练样本数据集作为因变量并进行模糊回归。由于重灾数据样本较少，本文将灾情等级划分为三个等级(Ⅰ类轻灾、Ⅱ类中灾、Ⅲ类重灾)，每个等级对应的三角模糊数如图2所示。

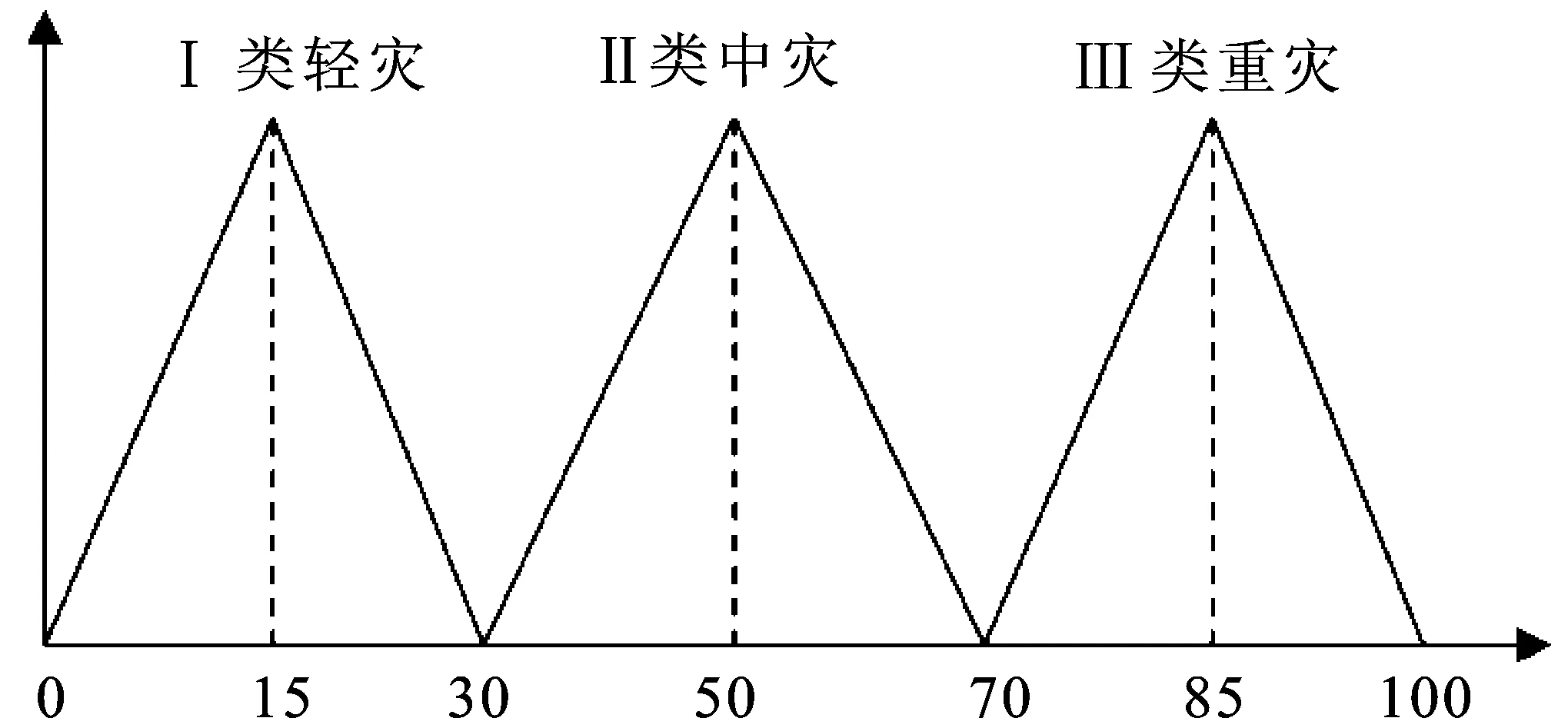
图2 模糊语言等级隶属度函数图

首先，为考察灾情等级与影响因素指标之间的关系，根据洪水灾害的灾情数据集，以灾情等级y为因变量，以倒房x1、受灾面积x2、伤亡人数x3、经济损失x4为自变量，建立下列模糊多元回归模型：

yi=(ymi,αli，βui)

=(k1,α1，β1)x1i+(k2,α2，β2)x2i+

(k3,α3，β3)x3i+(k4,α4，β4)x4i

(i=1,2,…,40)

为了估计上述模糊回归方程的回归参数，将表1的自变量样本数据和因变量模糊隶属度(图2)代入式(15)，则可得模糊回归方程如下：

y=(0.180 1,0,0.446 3)x1+

(0.011 6,0,0.022 2)x2+

(0.011 3,0,0.021 0)x3+

(2.705 0,0,0.183 0)x4

为了说明上述模糊回归方程的有效性，将表2的测试样本数据代入上述方程，可得模糊回归因变量输出y，如表2所示，可知因变量y值也是一个模糊数。

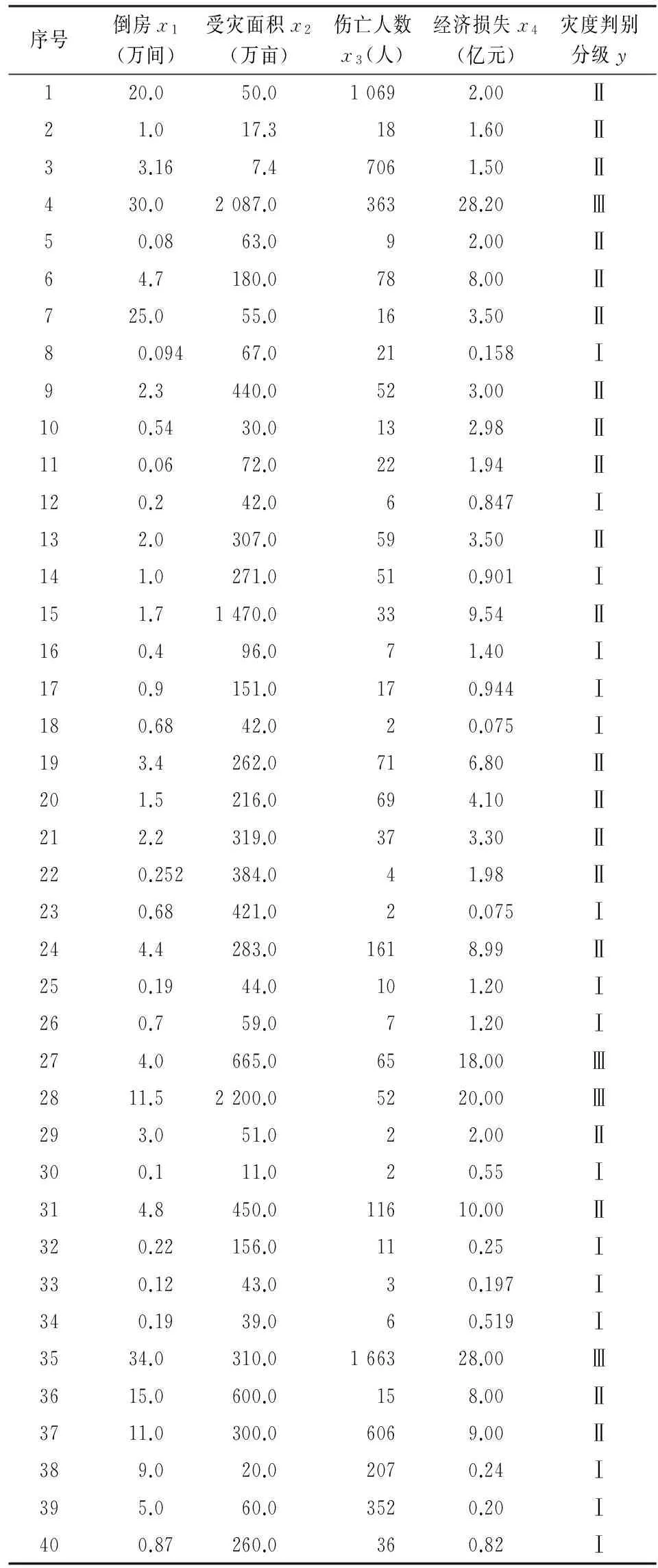
表1 洪水灾情样本数据表

为了得到具体的定性灾情等级，利用可能性均值-标准差距离公式(6)计算因变量模糊数y与灾情等级模糊数之间的距离，距离越小越接近于该灾情等级。测试样本与三个灾情等级之间的距离如表3所示。

由表2可知，测试分级结果与实际分级基本一致，5个测试样本中仅有样本43与灾度判别结果不同，通过分析发现样本43是山东省龙卷风所引起的自然灾害，由于龙卷风所造成的次生灾害和经济损失相对较小，因此本文将其分级为Ⅰ类轻灾。对于样本44，灰云聚类方法将其分级为Ⅱ类中灾，本文方法与灾度判别方法都将其分级为Ⅲ类重灾，事实上由表3可知，样本44与Ⅱ类中灾的距离为17.917 6，与Ⅲ类重灾的距离为17.363 4，所以，样本44介于Ⅱ类中灾和Ⅲ类重灾之间偏向于重灾。虽然，基于模糊回归模型的分级方法还不是完全精确，但它是一种建立在不确定数据驱动基础上的客观方法，并且具有一定自学习能力(训练样本变化，模糊回归参数也变化)，易于计算机操作，能够有效避免分级过程中的收集数据不精确性、决策者的主观性和随意性。

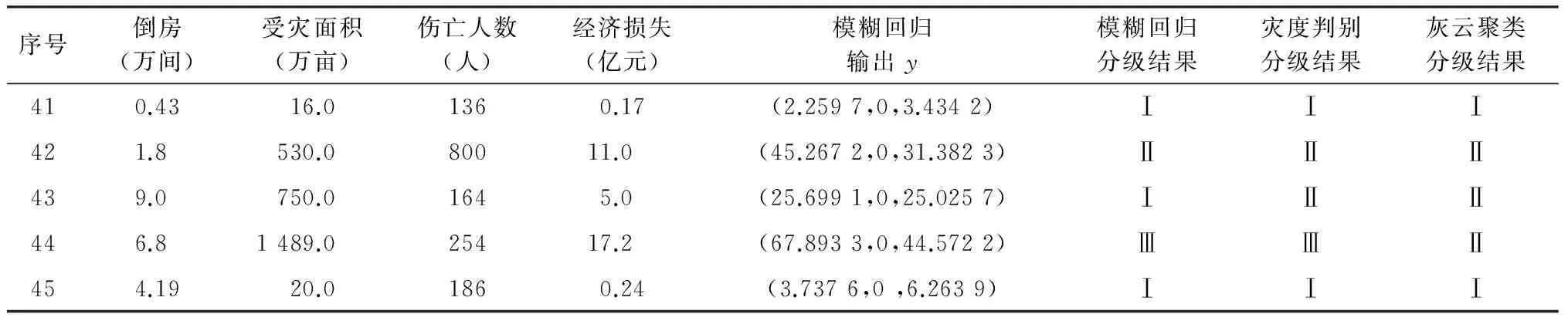
表2 对测试样本的分级结果表

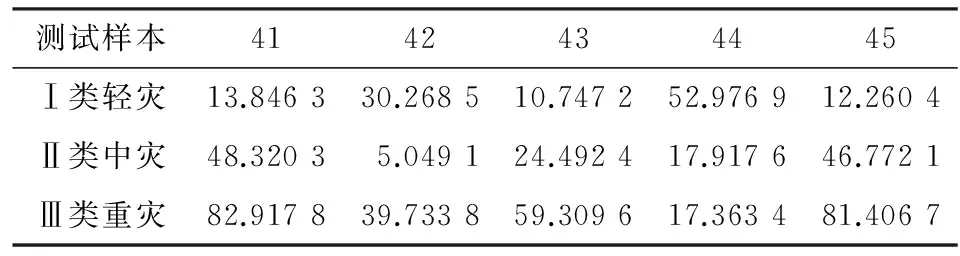
表3 测试样本与三个等级之间的距离表

五、结 论

自然灾害事件分级受诸多模糊不确定性因素的影响，是一个极其复杂的问题。本文将模糊线性回归模型应用于洪水灾害事件的等级评估问题，描述了基于模糊回归模型的自然灾害事件分级方法的具体过程，给出了验证该方法可行性的洪水灾害等级评估实例。针对采样数据信息的不确定性和分级等级的模糊性，构建指标影响因素和分级等级之间的模糊回归模型，采用可能性均值-标准差距离最小二乘估计方法对模糊线性回归模型的参数进行估计，通过对样本数据进行处理，通过测试，得到了比较符合实际的结果。实例表明，基于模糊回归模型的灾害事件分级方法是可行且有效的，相比其他方法，本文的方法具有良好的拟合效果，且计算简单，有利于决策者根据分级结果科学分配应急资源，提出合理的应急处置措施，提高决策的准确性、及时性和科学性。当然在本文的模糊回归模型中，采用的是三角模糊数表示模糊信息，而不同的模糊数是否对分级结果有影响，这将是下一个应该讨论的问题。

参考文献：

[1] 商丽媛，谭清美.基于支持向量机的突发事件分级研究[J].管理工程学报，2014，28(1).

[2] 李祚泳，邓新民.自然灾害的物元分析情评估模型初探[J].自然灾害学报,1994，3(2).

[3] 吴凤平,程铁军.基于改进的灰色定权聚类分析的突发事件分级研究[J].中国管理科学,2013(21).

[4] 宋莎莎,戴锋,卫保璐.基于模糊层次分析法和聚类分析的突发事件分级研究[J].科学决策,2010(10).

[5] 蔡正杰,梁昌勇,赵树平.突发环境事件等级评估方法研究[J].计算机应用研究,2014，31(11).

[6] 黎育红，陈玥.基于灰云白化权函数的洪水灾害综合等级评估[J].自然灾害学报,2013，22(1).

[7] 张艳琼,陈祖琴,苏新宁.基于云模型的突发事件分级模型研究[J].情报学报,2015，34(1).

[8] Carlsson C,Fullér R.On Possibilistic Mean Value and Variance of Fuzzy Numbers[J].Fuzzy Sets and Systems，2001,122(2).

[9] Tanaka H，Uejima S，Asai K.Linear Regression Analysis with Fuzzy Model[J].IEEE Transactions on Systems Man，and Cybernetics，1982,12(6).

[10] 柏林，房勇.基于模糊回归分析的投资组合选择模型[J].系统工程理论与实践，2015,35(7).

[11] 卢佩,陆秋君.模糊线性回归模型的最小二乘方法[J].统计与信息论坛,2016,31(2).