基于摄动法的相变材料熔点附近热导率测量方法

周天，刘旭，孙志强，彭伟，周孑民



基于摄动法的相变材料熔点附近热导率测量方法

周天1, 2，刘旭1，孙志强1，彭伟1，周孑民1

(1. 中南大学 能源科学与工程学院，湖南 长沙，410083；2. 中南大学 材料科学与工程学院，湖南 长沙，410083)

以Stefan半无限大理论为基础，建立柱坐标系下一维径向相变传热的数学模型；运用摄动法推导相变材料熔点处液相热导率与相界面移动规律之间的测量模型，基于此模型设计一套测量相变材料熔点附近热导率的测量系统。采用相变蓄热系统中常用的结晶水合盐——八水氢氧化钡作为实验对象，分别在热边界温度为356，361和366 K时进行实验，通过测量相界面的移动变化规律，计算得到相变材料的热导率。研究结果表明：在这3个热边界温度下，相变材料液相热导率测量平均值分别为0.673，0.658和0.651 W∙m−1∙K−1；采用该方法进行测量时，只需控制热源边界温度，无需测量热流密度，1次实验即可获得多组热导率，测量精度较高，具有较强实用性。

相变材料；相变过程；摄动法；热导率

近年来，随着环境污染、资源短缺等各种问题经常出现，太阳能、风能等新能源技术的应用日趋广泛，但这些技术都存在能量在时间与空间不匹配之间的矛盾。相变蓄热技术作为解决这一矛盾的有效手段，得到广泛关注与应用[1−10]。相变材料作为相变蓄热系统中的能量载体，其熔点附近的热导率与传热过程密切相关，它不仅是衡量相变储能材料能量储存与交换效率的依据，同时也是绝热设计、分析计算及工程设计中不可或缺的重要参数[11]，相变材料热导率的测量一直是国内外相关领域的研究热点[12−13]。TUFEU等[14]利用同心圆柱法测得碳酸钠、硝酸钾、亚硝酸钠等多组熔盐及其混合物的热导率，测量误差在4%以内，并发现混合物的热导率基本遵循混合法则。TIAN等[15]利用热线法测得质量分数为50%的聚丙烯酸水溶液和质量分数为50%的聚丙烯酸钠水溶液在压力为1×105Pa、温度从299 K变化到368 K的热导率，并得到精度较高的结果，其误差控制在±4%之内。ZHAO等[16]应用3ω法及谐波检测技术得到脲醛和石蜡切片组成的相变材料微胶囊的热导率与其密度、温度之间的关系，发现相变材料微胶囊的热导率与密度相关，其值随着密度的增大而增大；另外，当温度升至相变温度时，由于固相导热与气相传热的影响，热导率测量值在此时达到峰值。HUANG等[17]利用差示扫描量热法测量了一种相变乳液的热容，乳液中石蜡的质量分数为30%，结果表明乳液的热容由水和石蜡的显热热容和潜热热容2部分组成。然而，这些传统的热导率测试方法中，无论是稳态测试方法还是非稳态测试方法，都需要给被测物质施加1个温度梯度，这样往往会改变相变过程中被测物质的结构、晶型及热物性性能，使测量结果失去真实性；另一方面，这些方法对样品的形状、体积等都有严格规定，测试样品需经过特殊加工，测试过程较复杂。LAMVIK等[18−19]提出利用Neumann理论研究物质在熔点附近的热导率，假设相变过程中固/液两相中温度场呈线性分布，用差分方式代替相界面处能量方程中的微分形式得到相变材料热导率与相界面移动速率间的测量模型，并测量了锡、铅、锌等快速淬火金属的热导率。蒋绍坚等[20−25]将相界面处能量方程与固/液相的能量微分方程相结合，联立求解的思想，并搭建了圆柱一维轴向相变实验系统，对铂、锌、铝、镓、伍德合金等多种金属和硝酸钠、硝酸钾等熔盐物质进行测量，得到精度较高的实验结果。为此，本文作者将Stefan半无限大理论扩展，建立柱坐标系下一维径向相变传热模型，运用摄动法推导一维径向模型下相变材料熔点处液相热导率与相界面移动规律的关系式，搭建动态热导率测量系统，测量八水氢氧化钡的热导率。

1 测量原理

将Stefan半无限大理论扩展至柱坐标系，其一维径向熔化过程如图1所示。相变材料充满整个圆柱形区域，并维持在相变温度m附近，上、下端面绝热。在初始时刻即=0 s时，壁面温度突然升高至0(0＞m)，相变材料吸收热量开始熔化，并向固相区域扩散，热量由液相区域流向固相区域。

图1 一维径向Stefan模型的熔化过程

液相区域导热微分方程为

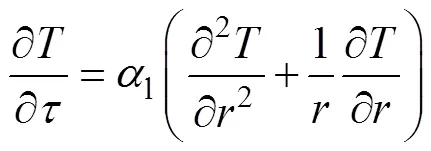
当时间＞0 s时，=0处的温度=0，即(0，)=0；当=0时，=处的温度=m，即(, 0)=m。

相界面处能量方程为

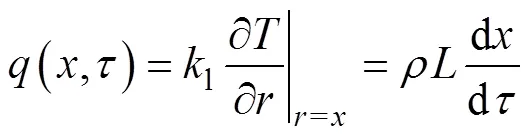
式中：l为相变材料的液相导温系数，m2/s；为时间，s；为相变材料密度，kg/m3；l为相变材料的液相热导率，W·m−1·K−1；为相变材料的潜热，J/g；为热流密度，kJ·m−2·s−1；为径向坐标；0为相变室内径，mm；，0和m分别为温度、热源温度、相变温度，K；为相界面位置，mm。

从式(1)和(2)可以看出：通过求解相界面位置随时间变化的关系和液相区域相变材料温度分布情况，即可获取相变材料熔点附近液相的热导率。但由于相变过程是复杂的非线性问题，因此，采用RILEY等[26−27]提出的摄动法求得其近似解。为了简化计算，将主要参数按下列方式进行量纲一处理：

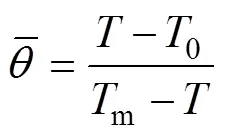
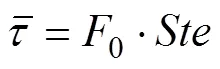
式中：l为相变材料液相比热容；为固定热边界温度下的斯蒂芬数；为傅里叶数。则液相区域的导热微分方程化为

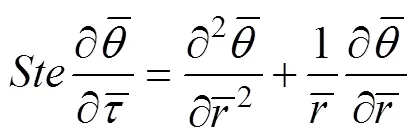
边界条件化为

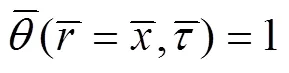
相界面位置化为

将式(12)代入式(8)~(11)，合并同阶项可得：

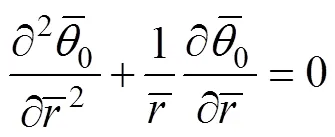
边界条件为

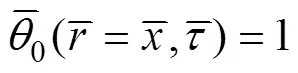
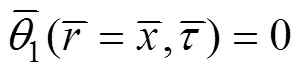
联立式(14)~(19)求解得

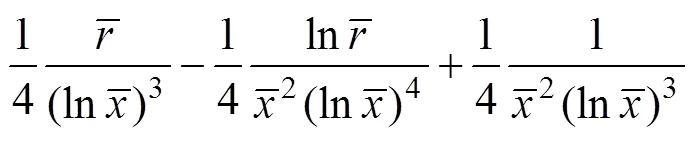
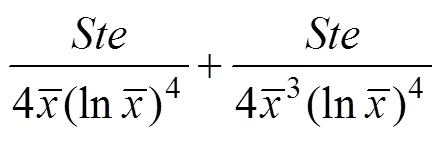
经积分可得

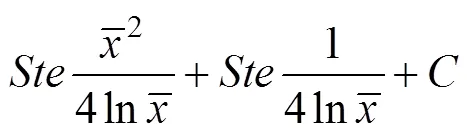
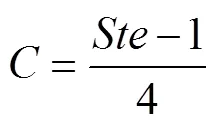
则

将无因次参数回代入式(24)，即可得到相变材料液态热导率与相界面位置和相变时间之间的关系式：

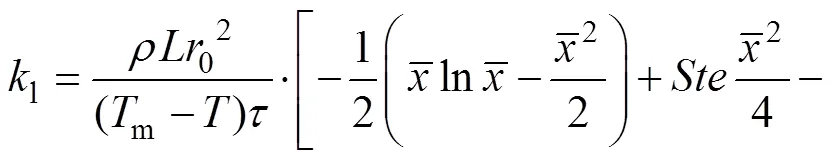
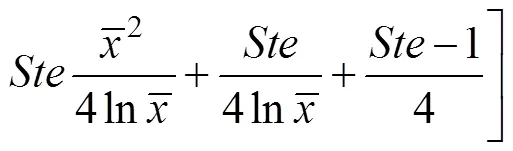
2 实验装置与条件

2.1 实验装置

根据相变材料熔点处液相热导率与相界面位置、时间的关系式，设计了如图2所示的热导率测量系统。整个测量系统分为炉体及相变室、加热及控温系统和相界面探测系统共3部分。

2.1.1 炉体及相变室

相变室盛放被测物质的容器，同时也是相变过程发生之处。在实验过程中选用铝制圆筒作为相变室，以保证相变室壁面热源边界温度可以快速达到均匀状态，同时又不与被测物质反应。相变室内径为88 mm，外径为96 mm，底部厚度为5 mm，相变室高度为 135 mm。炉体起保温作用，确保热源边界温度可以尽快达到给定值。其结构示意图如图3所示。

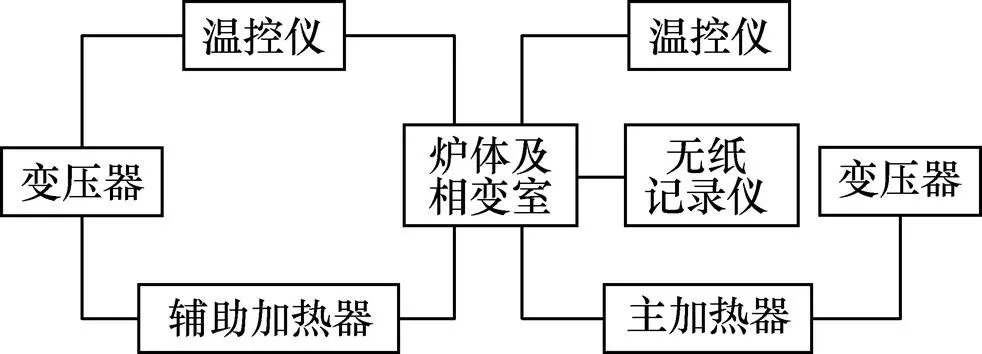
图2 实验测试系统示意图

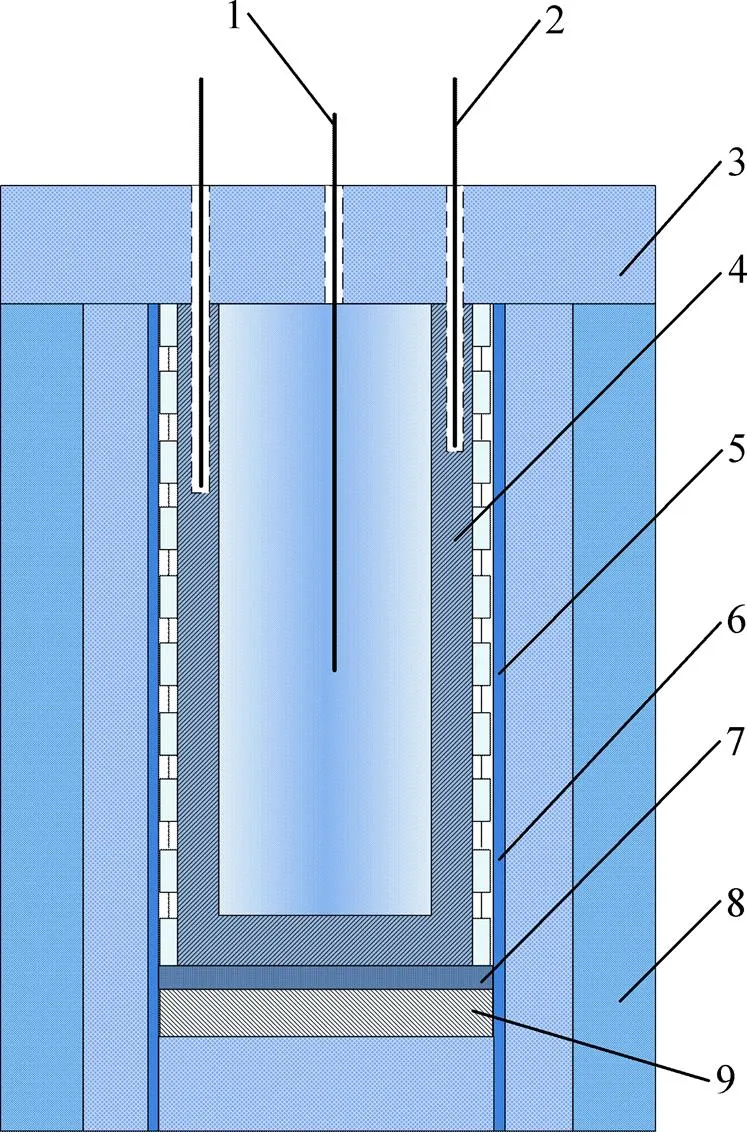
1—中心热电偶；2—壁面热电偶；3—硅酸铝保温棉；4—相变室；5—主加热器；6—橡胶垫；7—辅助加热器；8—保温层；9—垫片。

2.1.2 加热及控温系统

加热及控温系统是确保相变过程发生在理想边界条件的决定性因素。加热及控温系统可分为温度检测装置、温度控制装置和加热装置。本研究中用到2个加热元件：主加热器和轴向辅助加热器。主加热器选用电阻加热方式，加热元件由铁铬铝电阻丝和防止相邻电阻丝短路、保证整体结构稳定性的绝缘套管编制而成，以确保热源边界温度在短时间内能达到给定值。轴向补偿加热器选用硅橡胶加热片，置于相变室底部，与主加热器配合使用。实验中轴向加热器需一直维持在相变温度m附近，以减小轴向热流量损失。温度检测元件采用K型热电偶，分别布置于图4中的6个筒身测温孔及中心测温孔中，实时监测相变材料内部的温度变化，确保测量在均一、稳定的温度条件下进行，同时记录边界面上温度变化。将采集的温度信号输入PID温控仪中，再反馈给执行单元。

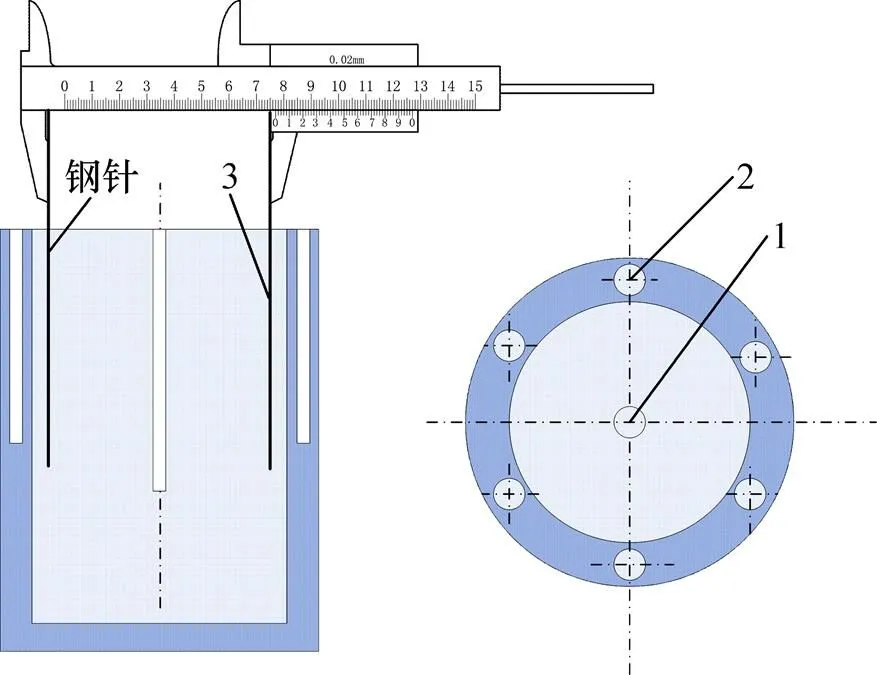
1—测温孔；2—筒身测温孔；3—钢针。

2.1.3 相界面探测系统

在理想情况下相变材料内部温度均匀分布，相变过程均匀向内进行，相界面为规则的圆柱面。因此，可采用直接接触的测量方法，选用直径为0.5 mm、刚性良好的合金钢针，其上端固定在数显游标卡尺的2个外测量爪的内侧。测量时可通过移动测量爪控制钢针来夹取相界面直径，在同一时刻换不同角度夹取2次，求其平均值，以提高测量精度。主要实验设备型号及参数如表1所示。

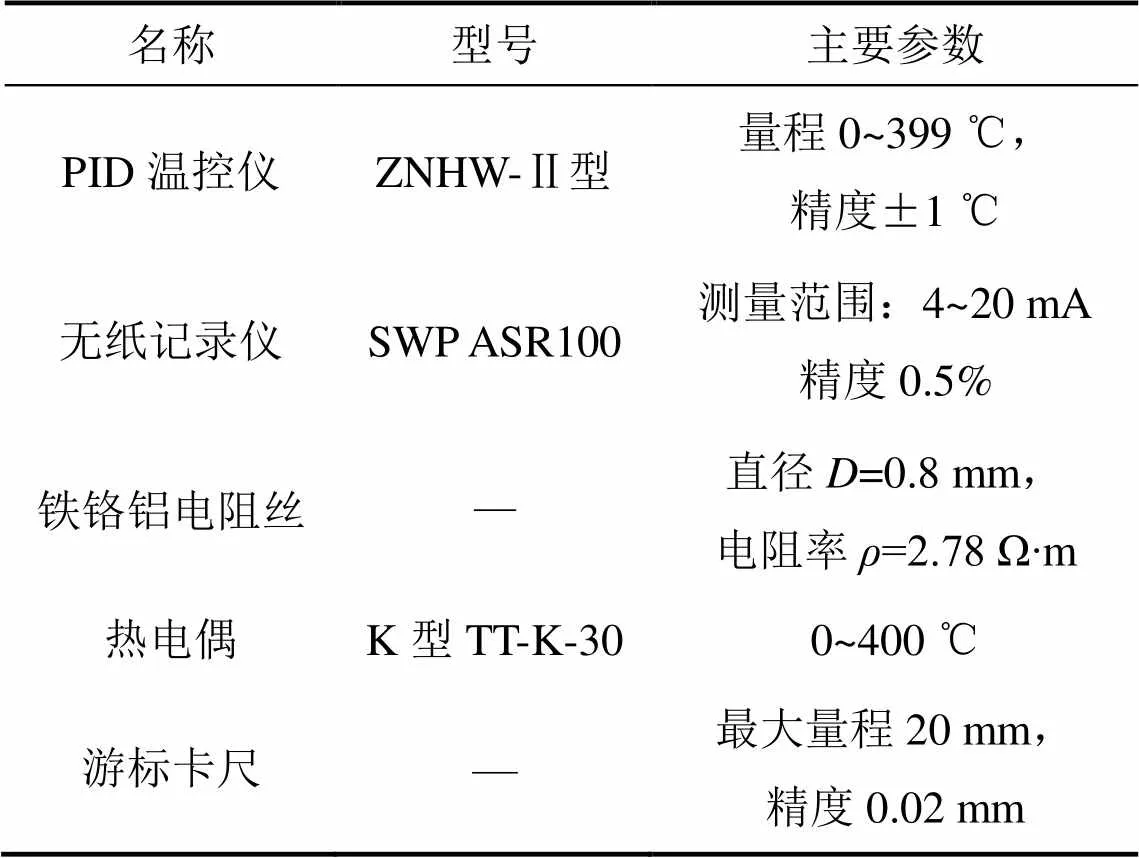
表1 主要设备型号及相关参数

2.2 测量过程

无机水合盐储能密度大，导热性能好，相变温度一般在100 ℃以下，常用于中低温蓄热系统中[4]。本实验以熔点处热物性数据相对完整的八水氢氧化钡(Ba(OH)2·8H2O)(分析纯，上海国药集团化学试剂有限公司)作为测试对象。其相关热物性参数见表2[4]。

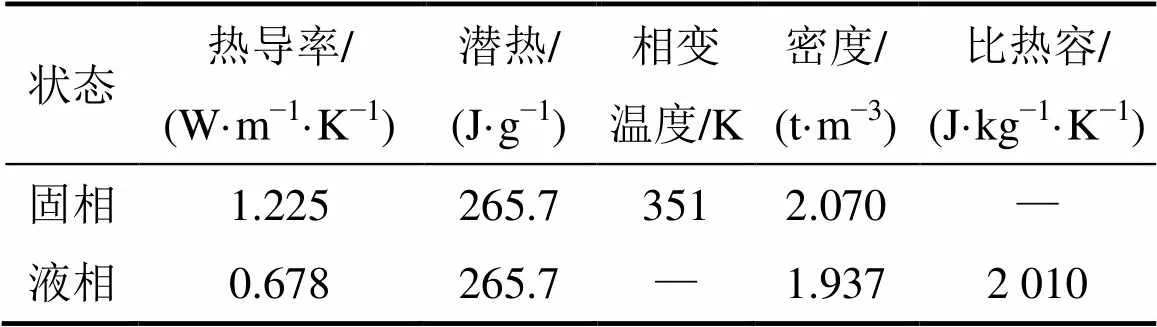
表2 文献[4]中氢氧化钡相关热物性参数

常温储存的八水氢氧化钡呈颗粒状。实验时，采用电炉低温加热至熔融状态后分层倒入相变室内，每层大约5 mm，待室温冷却40~50 min后，再倒入另一层，这样可有效避免凝固时样品中残留气泡影响热导率测量值准确性的问题。待装满相变室后，于室温存放一段时间，待无纸记录仪记录的中心热电偶温度达到室温并稳定后，调整PID温控仪控制主加热器及轴向补偿加热器使温度升高至相变温度m附近并维持在稳定状态，直至无纸记录仪记录的中心热电偶温度达到相变温度附近并稳定后，再次调整PID温控仪控制主加热器的温度至给定的热源边界温度即356，361和366 K，过一段时间后可开始测量。由于圆柱相变数学模型中对时间没有特殊要求，原则上可以在任意时刻测量。本研究考虑到探测工具自身的尺寸、升温时热扰动不稳定及熔化到一定程度时液相增多对流换热增强等问题，相界面位置至轴的距离控制在30~42 mm。开始测量后每隔3 min测1次，每次在不同径向上测2组相界面位置数据。将测得的相界面位置与时间的关系代入式(25)即可计算得到相变材料熔点处液相的热导率。

3 结果及误差分析

为了验证测试系统的可行性与灵敏性，实验前采用正二十烷进行验证实验，使用本研究中的探测方法可以发现在固−液相界面处有明显的固液分离模糊区。这是由于正十二烷为非晶体，其相变过程发生在一定温度区间内。JONES等[28]研究了上、下端面绝热、壁面温度突然升高的圆柱径向模型下正二十烷的熔化过程，发现由于实验时样品中难免存在一些微小气泡，随着样品的熔化，气泡受浮力的驱动向相变室的上端面移动，因此，靠近上端面部分的局部对流换热增强，随着熔化过程的进行，相变材料呈圆台形熔化。在本研究中，由于测量相界面的需要，在上端面没有添加温度补偿装置，因此，在实验过程中，浮力驱动的自然对流与上表面热损失相互抵消，固相区域在熔化过程中基本保持为圆柱形。图5所示为热源边界温度0=361 K，升温时间=1 860 s时八水氢氧化钡熔化实物图。从图5可以看出：固液两相被1个明显的交界面分隔，界面呈圆柱形；同时，由于上端面存在热损失，在已经熔化的液相区域上部，一些液相的熔盐又重新成核并凝固于表面。

图5 T0=361 K，τ=1 860 s时熔化实物图

用探针测量相界面位置，相界面位置与时间变化的关系如图6所示。从图6可以看出：在3组不同热源边界温度下，相界面位置移动规律均呈双曲线变化趋势。由于初始时刻界面处的温度梯度较大，因此，经过界面处的热流密度大，此时相界面移动速率快；随着熔化过程进行，相界面处的温度梯度逐渐变小，从而相界面的移动速率逐渐变小。随着熔化过程继续进行，相界面处的温度梯度继续减小，当相界面处的吸热与相变室的热损失基本达到一种动态平衡状态时，熔化动力减小，熔化过程则变得非常缓慢。当=1 320 s，热边界条件0=356 K时，相界面移动并不明显，此时，还难以利用探针测量界面的变化情况。这是由于在测量中，相变材料的初始温度略低于相变温度，因此，需要吸收一定的显热并升至相变温度后再熔化。而在热边界条件0=361 K下，相界面在=1 320 s时已清晰可见，其平均位置为38.515 mm。当=1 860 s时，热源温度0分别为356，361和366 K时相界面位置平均值分别为39.51，37.33和35.12 mm。由此可以看出热源边界温度越高，熔化速度越快，相界面位置越小，表明测量装置中的实际熔化过程与测量模型所示结果相符。

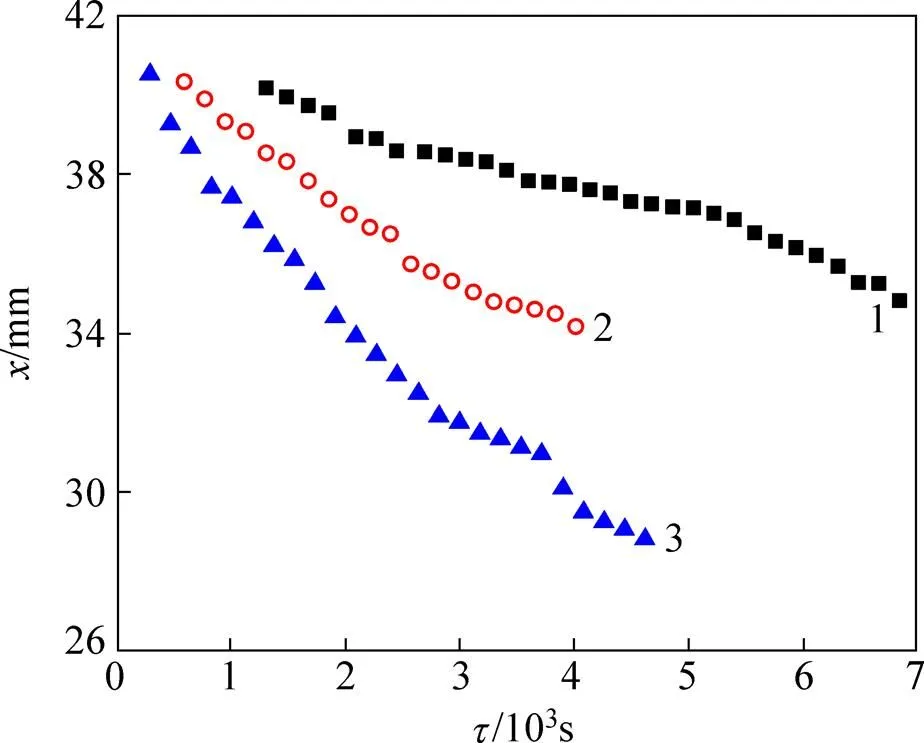
T0/K：1—356；2—361；3—366。

图7所示为3种热边界条件下，计算得到的热导率随着熔化过程进行的变化关系。从图7(a)和图7(b)可以看出：在边界温度为361 K和366 K的实验条件下，热导率测量结果，基本呈现出先小于热导率平均值而后大于平均值，最后又小于热导率平均值的变化趋。在整个测量区间内，测得的热导率首先从0.6 W·m−1·K−1上升至0.7 W·m−1·K−1附近，随后下降至0.65 W·m−1·K−1。这是因为在实际测量中，相变材料的起始温度略低于相变温度，在边界升温后，相变材料需要吸收一定的显热达到相变温度后才开始熔化；同时，由于外壁温升过程需要一定的时间，而在测量模型式(25)中的温度边界是瞬间变化的理想情况，因此，在测量初始阶段，测量得到的界面位置偏大，导致得到的热导率偏小。而随着熔化过程的进行，由于对于不同的绝热设计，相变室的上、下端会出现温差，熔化的液相区域会发生自然对流现象，此时，热传导不再是影响相界面移动规律的唯一因素。因此，在自然对流的影响下，测量得到的相界面位置会偏小，从而使得热导率偏大。当熔化过程进行到后期时，由于界面处的热流密度逐渐减小，上端的热损失对界面移动的影响增大，所以，测量得到的相界面位置偏大，而热导率则逐步减小，对于图7(a)，当=3 900 s以后，由图6可以看出，此时相界面位置已小于30 mm，不在本次测量的范围内。

T0/K：(a) 366；(b) 361；(c) 356

另一方面，图7(c)中热导率呈先大于热导率平均值而后小于平均值，最后又大于平均值的变化规律。这是因为当热源边界温度为356 K时，较小的边界温度变化使熔化过程偏慢，在测量的初始时刻，采用钢针进行测量会对界面边界产生挤压破坏，因此，初始时刻的界面测量值偏小，得到较大的热导率。而当相界面位置小于36 mm时，热导率计算值逐渐大于平均值，这是因为当熔化进行到一定阶段时，受浮力驱动，对流换热不断增强，换热加剧，熔化速率相比理想状态快，相界面测量值小于理想值，热导率测量值又不断增大。

实际边界温度与理想边界温度的对比见图8。

1—实际边界条件；2—理想边界条件。

从上述分析可以看出，非理想温度边界条件、相变室上端面的热损失是影响测量结果的主要因素。其中，非理想温度边界条件、相变室上端面的热损失使热导率测量结果偏小，而液相区域的自然对流、测量时装置对界面的破坏会导致热导率测量结果偏大。随着测量过程的进行，由于不同影响因素的耦合及其变化，热导率的测量值在真值附近不断地波动。因此，可以将测量过程中所得到的热导率平均值作为最终测量结果，在3种温度边界下，相变材料熔点附近液相的热导率平均值分别为0.673，0.658和0.651 W·m−1·K−1，与文献[4]中结果0.678 W·m−1·K−1相比，相对误差都在4%以内，测量结果精确度较高。与现有的测试方法相比，本文所提出的热导率测量模型简单，仅需在控制边界温度的前提下，通过获取相界面的移动规律即可得到热导率，无需测量热流量、温度等参数；此外，通过1次实验可得到多组热导率，可以有效降低每次测量中引入的随机误差；测量装置简单，无需对测试对象进行复杂加工。因此，本方法具有一定的应用前景。使用上述测量手段可以简单、方便地获得相变材料熔点处的热导率，但由于理论模型较简易、边界条件较理想并受控制设备的局限等，实验结果存在一定误差。

4 结论

1) 在边界温度为356，361和366K时测得的八水氢氧化钡熔点附近液相热导率平均值分别为0.673，0.658和0.651 W·m−1·K−1，测量相对误差小于4%。

2)只需在较小的边界温度变化的前提下测量相界面所在位置随时间的移动规律，无需测量热流密度等其他常规热物性检测参数即可得到热导率，可较好地反映被测物质的真实物理性质。

3) 测试设备简单，易于控制，无需对试样进行复杂加工，并且1次实验即可测得多组热导率，测试结果精度较高，具有较强的实用性。

[1] FOKAIDES P A, KYLILI A, KALOGIROU S A. Phase change materials (PCM) integrated into transparent building elements:a review[J]. Material for Renewable and Sustainable Energy, 2015, 4(6): 1−13.

[2] AGYENIM F, HEWITT N, EAMES P, et al. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems(LHTESS)[J]. Renewable and Sustainable Energy Reviews, 2010, 14(2): 615−628.

[3] DUTIL Y, ROUSSE D R, SALAH N B, et al. A review on phase-change materials:mathematical modeling and simulations[J]. Renewable and Sustainable Energy Reviews, 2011, 15(1): 112−130.

[4] ZALBA B, MARÍN J M, CABEZA L F, et al. Review on thermal energy storage with phase change materials,heat transfer analysis and applications[J]. Applied Thermal Engineering, 2003, 23(3): 251−283.

[5] LI Saiwei, ZHOU Tian, SUN Zhiqiang, et al. External forced convection from circular cylinders with surface protrusions[J]. International Journal of Heat and Mass Transfer, 2016, 99: 20−30.

[6] BAHRASEMAN H G, LANGURI E M, EAST J, et al. Fast charging of thermal energy storage systems enabled by phase change materials mixed with expanded graphite[J]. International Journal of Heat and Mass Transfer, 2017, 109: 1052−1058.

[7] LV Peizhao, LIU Chenzhen, RAO Zhonghao. Experiment study on the thermal properties of paraffin/kaolin thermal energy storage form-stable phase change materials[J]. Applied Energy, 2016, 182: 475−487.

[8] CUNHA J P D, EAMES P. Thermal energy storage for low and medium temperature applications using phase change materials-A review[J]. Applied Energy, 2016, 177: 227−238.

[9] CUI Yaping, XIE Jingchao, LIU Jiaping, et al. A review on phase change material application in building[J]. Advances in Mechanical Engineering, 2016, 9(6): 1−15.

[10] KAPSALIS V, KARAMANIS D. Solar thermal energy storage and heat pumps with phase change materials[J]. Applied Thermal Engineering, 2016, 99: 1212−1224.

[11] 叶锋, 曲江兰, 钟俊瑜, 等. 相变储热材料研究进展[J]. 过程工程学报, 2010, 10(6): 1231−1238.YE Feng, QU Jianglan, ZHONG Junyu, et al. The research of phase change material[J]. The Chinese Journal of Process Engineering, 2010, 10(6): 1231−1238.

[12] BERTELLI F, CHEUNG N, FERREIRA I L, et al. Evaluation of thermophysical properties of Al-Sn-Si alloys based on computational thermodynamics and validation by numerical and experimental simulation of solidification[J]. The Journal of Chemical Thermodynamics, 2016, 98: 9−20.

[13] AFRAND M. Experimental study on thermal conductivity of ethylene glycol containing hybrid nano-additives and development of a new correlation[J]. Applied Thermal Engineering, 2017, 110: 1111−1119.

[14] TUFEU R, PETITET J P, DENIELOU L, et al. Experimental Determination of thermal conductivity of molten pure salts and salt mixtures[J]. International Journal of Thermophysics, 1985, 6(4): 316−335.

[15] TIAN F, SUN L, MOJUMDARS C, et al. Absolute measurement of thermal conductivity of poly(acrylic acid) by transient hot wire technique[J]. Journal of Thermal Analysis and Calorimetry, 2011, 104(3): 823−829.

[16] ZHAO Gangtao, XU Xiaohui, QIU Lin, et al. Study on the heat conduction of phase-change material microcapsules[J]. Journal of Thermal Science, 2013, 22(3): 257−260.

[17] HUANG L, NOERES P, PETERMANN M, et al. Experimental study on heat capacity of paraffin/water phase change emulsion[J]. Energy Conversion and Management, 2010, 51(6): 1264−1269.

[18] LAMVIK M. Determination of thermal diffusivity of solid material near the melting point[J]. International Journal of Thermophysics, 1982, 3(1): 80−87.

[19] LAMVIK M, ZHOU J M. A novel method for measuring the thermal conductivity of metallic materials during melting and solidification[J]. Measurement Science and Technology, 1995, 6: 880−887.

[20] 蒋绍坚, 周孑民, 杨怀东, 等. Pb,Zn和Al在熔点附近的热导率测试[J]. 金属学报, 2000, 36(3): 334−336.JIANG Shaojian, ZHOU Jiemin, YANG Huaidong, et al. Determination of thermal conductivities of Pb,Zn and Al about melting point[J]. Acta Metallurgica Sinica, 2000, 36(3): 334−336.

[21] 周孑民, 杨怀东, LAMVIK M, 等. 伍德合金相变过程中固、液相熔点热导率的测定[J]. 工程热物理学报, 2000, 21(1): 89−92. ZHOU Jiemin, YANG Huaidong, LAMVIK M, et al. Determination of thermal conductivity of wood’s metal at melting point during phase transition[J]. Journal of Engineering Thermophysics, 2000, 21(1): 89−92.

[22] 李长庚, 周孑民. 相变材料相变点温度热物性的测试及误差分析[J]. 热能动力工程, 2004, 19(1): 45−47. LI Changgeng, ZHOU Jiemin. Thermal conductivity determination and error analysis of phase change material[J]. Journal of Engineering for Thermal Energy and Power, 2004, 19(1): 45−47.

[23] 詹水清, 周孑民, 吴烨, 等. 高温熔盐热物性的动态测定与误差修正方法[J]. 化工学报, 2012, 63(8): 2341−2347. ZHAN Shuiqing, ZHOU Jiemin, WU Ye, et al. Dynamic measurement of thermophysical properties of molten salt and error correction method[J]. CIESCC Journal, 2012, 63(8): 2341−2347.

[24] PENG Wei, ZHOU Jiemin, LI Yuan, et al. A dynamic technique for the measurement of thermal conductivity of molten salt based on cylindrical melting model[J]. Journal of Thermal Analysis and Calorimetry, 2014, 115(2): 1767−1777.

[25] ZHOU Tian, LIU Xu, LI Yuan, et al. Dynamic measurement of the thermal conductivity of phase change materials in the liquid phase near the melting point[J]. International Journal of Heat and Mass Transfer, 2017, 111: 631−643.

[26] RILEY D S, SMITH F T, POOTS G. The inward solidification of spheres and circular cylinders[J]. International Journal Heat and Mass Transfer, 1974, 17: 1507−1516.

[27] PEDROSO R I, DOMOTO G A. Derturbation solutions for spherical solidification of saturated liquids[J]. ASME Journal of Heat Transfer, 1973, 95: 42−46.

[28] JONES B J, DAWEI S, SHANKAR K, et al. Experimental and numerical study of melting in a cylinder[J]. International Journal of Heat and Mass Transfer, 2006, 49(15/16): 2724−2738.

(编辑 陈灿华)

Thermal conductivity measurement of phase-change material near melting point based on perturbation method

ZHOU Tian1, 2, LIU Xu1, SUN Zhiqiang1, PENG Wei1, ZHOU Jiemin1

(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China; 2. School of Materials Science and Engineering, Central South University, Changsha 410083, China)

A new one-dimensional radial model was established based on the Stefan model. With the application of perturbation, the relationship between the thermal conductivity and the evolution of phase change interface was deduced. According to this relationship, a test system was designed to determine the thermal conductivity near the melting point of phase change materials. Barium hydroxide that was commonly used as materials in heat storage system was selected to obtain the thermal conductivity on the phase interface evolution at three boundary temperatures of 356, 361 and 366 K. The results show that the three average thermal conductivities are 0.673, 0.658 and 0.651 W∙m−1∙K−1, respectively. During the measurement, the control of boundary temperature is required, and the boundary heat flux needn’t be measured, and multiple sets of thermal conductivity can be obtained from a single test with high accuracy, so the proposed method has good applicability.

phase-change material; phase-change process; perturbation method; thermal conductivity measurement

O551.3

A

1672−7207(2018)04−0979−08

10.11817/j.issn.1672−7207.2018.04.028

2017−04−10；

2017−06−16

国家自然科学基金资助项目(51606224)；湖南省科技计划项目(2015RS4015)(Project(51606224) supported by the National Natural Science Foundation of China; Project(2015RS4015) supported by the Hunan Scientific Program)

孙志强，博士，教授，从事多相流测试技术、新能源与节能技术研究；E-mail：zqsun@csu.edu.cn