高速受电弓结构尺寸优化设计与仿真

安红战, 方蕾

（1.湖南铁路科技职业技术学院，湖南株洲 412006;2.湖南铁道职业技术学院，湖南株洲 412001）

0 引 言

随着高铁的出现与发展，电力机车的运行速度在不断地提高，这给人们的出行带了极大的便利。但电力机车能否安全、可靠地高速运行，不仅取决于它的牵引、制动和机械性能，还要受到受电弓的影响，并且受电弓的性能好坏往往是制约电力机车高速运行的关键。

受电弓是装在车顶上的一种电器装置，工作时受电弓升起，弓头与接触网接触将电流引入机车。在机车运行过程中，弓头要始终和接触网可靠接触，以保证机车供电的持续、稳定。由于接触网是一个质量和弹性都不均匀的弹性系统，而且其架设高度是不断变化的，在机车运行过程中，受电弓要能自动调整弓头的高度位置，同时在弓头位置变动过程中始终保持平动，这样才能保证运行中的受电弓滑板始终和接触网良好接触，同时均匀磨损，提高受流的可靠性和受电弓的使用寿命。因此，在进行受电弓设计时，首先要对弓头的运动轨迹进行优化设计，即合理确定受电弓各杆件的长度，使弓头在工作高度范围内得到非常接近竖直的运动轨迹且尽量做到平动。

1 结构分析

受电弓主要由弓头、框架、底架和传动机构等4部分组成[1]，如图1所示。弓头安装在受电弓框架的顶端，借助于框架的伸缩可上下移动，并能绕自身的固定转轴做少量的转动。框架用来支持弓头并传递运动，一般分为上下两部分，中间用铰链连接起来。底架即固定受电弓框架的底座，一般用型钢拼焊而成，具有较高的刚度，一般通过3个或4个绝缘子固定在车顶上。驱动装置用来提供升弓所需的动力，它将气缸或气囊的直线运动通过扇形板转化为升弓转矩，使下臂杆转动，驱动框架运动从而带动弓头上升。

图1 受电弓结构

2 建立运动方程

受电弓是一个空间机构，但它的主要运动是在一个竖直平面内，因此在进行运动分析时，可把受电弓看做一个平面4杆机构。图2为受电弓结构原理图，其中下臂杆AD是主动件，对应的升弓角为α，图中各尺寸的含义如表1所示。对受电弓的优化设计就是寻求这些设计尺寸的优化组合，确保受电弓的运动轨迹满足要求。由于实际的受电弓是空间结构，当把它抽象为一个平面连杆机构时，表1中的尺寸是指将各构件投影到竖直平面内后的尺寸，和构件的实际尺寸有所差异。

由于受电弓在整个运动过程中要求弓头平动且竖直升降，而弓头的平动可以看到弓头摆杆的平动，弓头的竖直运动可以看作上臂杆上E点的竖直运动。因此，在图2中，以A点为坐标原点，根据各构件的尺寸和运动关系，可以得到弓头的运动方程。

图2 受电弓结构原理图

表1 受电弓各几何尺寸的定义

1）弓头（上臂杆顶端E点）的运动轨迹方程

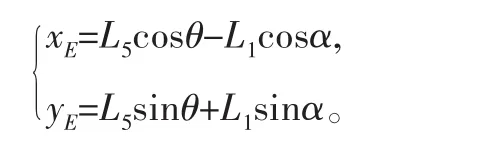
式中，xE、yE是设计变量L1、L3、L4、L5、a、b、γ的函数。

2）弓头的平动运动方程（弓头摆杆与水平方向的夹角）

式中:xF、yF为F点的坐标，即xF=L7cosλ－L2cos（α－μ），yF=L7·sinλ+L2sin（α+μ）；ρ为设计变量L1、L2、L3、L4、L5、L6、L7、a、b、γ、μ的函数。

3 构建优化模型

在进行单臂受电弓结构尺寸设计时，要满足下面几个方面的要求。

1）上框架E点在受电弓升降过程中应做垂直或近似垂直运动。在整个工作范围内，E点的运动轨迹在横向（x轴方向）的最大偏差不能超过50 mm。

2）弓头摆杆EF在受电弓的工作高度范围内尽量保持平动，以防止弓头转动而使前后滑板的受力不均影响弓头与接触网的良好接触。弓头摆角的最大偏差不超过3°。

3）受电弓的落弓高度为400 mm，上框架E点的工作高度范围（在y轴方向）为500～2400 mm。

上述1）、2）两项是受电弓结构尺寸设计的优化目标，3）是约束条件。弓头的运动轨迹和平动要求是L1、L2、L3、L4、L5、L6、L7、a、b、γ、μ这11个设计变量的函数，因此，这是一个多目标优化问题。对于多目标优化问题的处理，具有多种不同的优化方法，其中最主要的有2种：一种是将多目标问题转化成一个或一系列的单目标问题，另一种是直接求出非劣解就当多目标问题的解[7]。由于受电弓的运行轨迹取决于L1、L3、L4、L5、a、b、γ这7个参数的组合，而弓头的平动主要受L2、L6、L7、μ这4个参数的影响。因此可以将受电弓的优化问题转化成2个单目标优化问题分别进行优化求解。

3.1 弓头运动轨迹优化模型的建立

根据受电弓在升、降弓过程中弓头的运动轨迹要求，弓头运动轨迹优化问题的目标函数确定为

受电弓工作时需要满足的运动要求就是弓头运动轨迹优化问题的约束条件，即：

3）为保证受电弓能自由运动，同时考虑结构工艺要求，各设计变量的取值范围为（尺寸单位为mm）：1400≤L1≤1750，900≤L3≤1246，150≤L4≤400，1800≤L5≤1850，760≤a≤770，130≤b≤140，167.3°≤γ≤160°。

3.2 弓头平动优化模型的建立

受电弓在工作过程中，要求弓头在升降的同时保持平动，尽可能不发生转动。弓头摆角ρ即是衡量弓头摆动程度的参数，在实际的升弓或降弓过程中是不断变化的。弓头平动的优化目标就是在L1、L3、L4、L5、a、b、γ参数已定的基础上，寻求L2、L6、L7、μ这些设计变量的优化组合，使弓头在升弓或降弓的过程中弓头摆角ρ的变化量达到最小。

弓头平动优化问题的目标函数确定为

式中，ρ（i）为升弓角α取第i个值时弓头摆角对应的第i个值。

图3 弓头（E点）的运动轨迹曲线

图4 弓头摆角与升弓高度之间的关系曲线

考虑运动要求和结构工艺要求，约束条件为（尺寸单位为毫米）：1400≤L2≤1750，80≤L6≤120，1810≤L7≤1880，1°≤μ≤2.1°。

4 优化结果分析

根据以上建立的受电弓优化目标函数及约束条件，利用MATLAB优化工具箱进行编程[3]，得到一组优化参数。图3、图4分别为弓头（E点）的运动轨迹仿真结果和弓头摆角与升弓高度之间关系的仿真结果。由图3和图4可知，受电弓在整个工作范围（yE=500～2400 mm）内，E点水平坐标的最大和最小值分别为863.6 mm和825.6 mm，弓头摆角ρ的最大和最小值分别为87.32°和84.86°。E点水平坐标的变化范围ΔxE=38 mm，小于规定的50 mm；弓头摆角ρ的变化范围Δρ=2.46°，小于3°，弓头几乎保持平动。从仿真结果来看，优化所得的参数完全满足设计要求。

5 结论

受电弓实质上是一个平面串联4杆机构，其运动特性完全由杆件的结构尺寸来确定。合理确定各杆件的长度是确保其运动轨迹符合要求的根本。

MATLAB作为一款出色的商业数学软件，不仅用于数值分析计算，利用为数众多的附加工具箱，也被广泛应用于控制、电气、机械、统计等各领域。在受电弓结构尺寸优化设计中，建立了数学模型之后，可以方便、快速地利用MATLAB的优化工具箱进行分析、求解，得到满足受电弓运动要求的各杆件的最优尺寸，这为受电弓的结构设计提供了一种简单、有效、可行的方法。

［参考文献］

[1] 吴积钦.受电弓与接触网系统[M].成都:西南交通大学出版社,2010.

[2] 李明.详解MATLAB在最优化计算中的应用[M].北京:电子工业出版社,2011.

[3] 赵继俊.优化技术与MATLAB优化工具箱[M].北京:机械工业出版社,2011.

[4] 王华伟.基于多体动力学的受电弓系统分析和仿真研究[D].杭州:浙江大学,2010.

[5] 邢海军.受电弓框架阻尼机构最优化设计[J].石家庄铁道学院学报,2002,15(1):8-11.

[6] 陈剑.平面4杆机构参数化设计及运动仿真研究与实现[J].现代设计与先进制造技术,2010,39(9):23-30.

[7] 孙靖民.机械优化设计[M].北京:机械工业出版社,2007.