底轴驱动式闸门受力分析及油缸参数化设计
2018-05-16
(水利部长春机械研究所,吉林 长春 130012)
底轴驱动式闸门是一种新型、可调控溢流挡水闸门,用于泄洪、水坝蓄水、城市景观建设等工程。闸门及底轴全部置于河道内,主要由闸门面板、圆柱形底轴、固定在底轴上的门页、支承底轴的若干固定支铰座、底侧止水、闸墩侧墙密封件、液压启闭机及拐臂等组成。布置在两侧启闭机室内的液压启闭机控制着闸门的启闭,闸门可双向、任意设计高度调节挡水位,超过控制水位时门顶可实现溢流,形成人工瀑布景观。近年来,在国内各项水利工程,尤其是城市水生态环境治理工程中应用十分广泛。
目前,大多数文献对底轴驱动式闸门如何进行受力分析论述很少,使设计过程中的受力计算缺乏准确参考,为实现底轴闸的系列化设计增添了难度。另外,在底轴驱动式闸门的设计过程中,液压启闭机油缸参数选取比较麻烦。完成底轴驱动式闸门受力分析并实现液压油缸的参数化设计,对提高底轴驱动式闸门的系列化设计效率和设计水平具有重要的意义。
底轴驱动式闸门受力模型如下图所示。
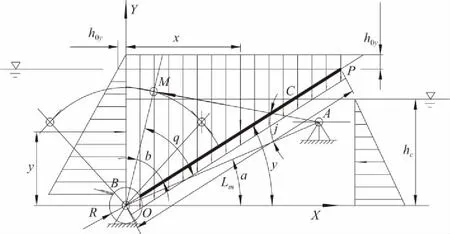
底轴驱动式闸门受力模型
为了分析底轴驱动式闸门的受力情况,推出具有普遍意义的计算方法,参照上图做如下几点说明:
a.油缸固定铰链点A和底轴中心O连线与水平轴成α角;油缸运动铰链点M和底轴中心O连线与闸门侧投影中心线成β角。
b.依据水利工程设计有关规范,闸门上沿在溢流状态下计算水面高度高于闸门上沿h0,是进行荷载计算的前提,在这个前提下讨论静水压力在水平方向与垂直方向的分布规律。
c.闸门下游水位位于底轴中心线以上hc。
为了求得液压油缸的设计参数,首先需要确定荷载(闸门自重和静水压力)对闸门底轴的作用力以及对底轴的作用力矩。闸门处于不同位置所受到的荷载不同,不仅底轴受到的水平、垂向静水压力不同,而且外荷载对底轴的作用力矩也不同。克服外荷载对底轴的力矩是油缸的职责,因此无论闸门处于什么位置,必须保证油缸有足够的能力克服荷载施加于底轴的力矩。通过对底轴所受荷载的受力分析进而可反向推出油缸需要的推力等设计参数。
1 上游静水压力对闸门的作用
将水对闸门的静水压力分为水平作用力和垂向作用力分别展开讨论;先讨论荷载分布规律进而研究两方向合力作用大小以及对闸门底轴的转矩。
假设闸门处于工作范围内任意位置,如图1所示。图中θ角、φ角以及闸门上沿P点下游水面与闸门的交线投影c点坐标随油缸的伸缩而变化。
1.1 静水压力水平分量对闸门的影响
1.1.1 水平力分布规律
依据水压与水深呈线性关系推导分布规律,参照受力模型图,设在纵坐标为y的位置荷载集度q(y),y的取值范围(yB,yP);闸门宽度为b,水的比重为γ。
当y=yP时:
q(yP)=h0bγ
(1)
当y=yB时:
q(yB)=(h0+yP-yB)bγ
(2)
根据两点[yB,q(yB)]和[yP,q(yP)]可得到直线分布函数:
(3)
将式(1),式(2)代入式(3)化简得
q(y)=bγ(h0+yP-y)
(4)
1.1.2 静水压力水平方向的合力

(5)
将式(4)代入式(5)积分并化简得
(6)
1.1.3 水平方向静水压力对闸门底轴的静矩

(7)
将式(4)代入式(7)积分并化简得
(8)
1.2 静水压力垂向分量对闸门的影响
1.2.1 静水压力垂向分量分布规律
参照受力模型图1,设在横坐标为x的位置荷载集度q(x),x的取值范围(xo,xP)。
当x=xP时,
q(xP)=h0bγ
(9)
当x=xo时,
q(xo)=(h0+yp)bγ
(10)
根据两点[xo,q(xo)]和[xP,q(xP)]可得到直线分布函数:
(11)
将式(9)、式(10)代入式(11)化简得
(12)
1.2.2 静水压力垂向分量的合力
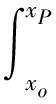
(13)
将式(12)代入式(13)积分并化简得
(14)
1.2.3 竖直方向静水压力对闸门底轴的静矩
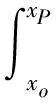
(15)
将式(12)代入式(15)积分并化简得
(16)
2 下游水位对闸门的作用
下游水位对闸门的作用与上游水位类似,计算方法完全相同,只是相应的力和力矩的方向与上游的方向相反。
2.1 静水压力水平方向分量影响
2.1.1 静水压力水平分量的合力
在式(6)中用hc替代yP,0取代yB,h0取值为零,则
(17)
与上游水静水压力Fx反向。
2.1.2 水平方向静水压力对闸门底轴的静矩
在式(8)中用hc替代yP,0取代yB,h0取值为零,则
(18)
与上游水闸门静水压力对闸门底轴力矩Mz,x反向。
2.2 静水压力垂直方向分量影响
2.2.1 静水压力垂直方向分量的合力
就下游水位对位闸门的作用而言,垂直方向的分量实际上就是闸门受到的下游液面、闸门和过底轴中心的垂线围城三角区域内排开的水对闸门的浮力。
在式(14)中用hc替代yP,xc替代xP,0取代xo,则
(19)
与上游水静水压力Fy反向。
2.2.2 竖直方向静水压力对闸门底轴的静矩
在式(16)中用hc替代yP,xc替代xP,0取代xo,则
(20)
与上游水闸门静水压力对闸门底轴力矩Mz,y反向。
3 闸门自重对底轴的作用
设闸门质量分布均匀总重Wm,面集度qm,闸门宽b;闸门与水平面夹角为ψ。闸门对底轴的作用力大小等于其自重Wm,方向向下,集度qm。
(21)
闸门对底轴的作用力矩:
(22)
4 油缸对底轴的作用
设油缸缸筒直径为D,活塞杆直径与缸筒内径比为k(无杆腔工作取k=0),液压系统压力为p。油缸克服静水压力以及闸门自重对底轴转矩所需的推力为Fm,则
(23)
油缸对底轴的力矩:
Mz.P=FmLmsinφ
(24)
对油缸最基本的要求是其对闸门底轴的力矩必须大于负载对底轴的力矩,即
Mz,P>Mz,x+Mz,y+Mm-Mz,xc-Mz,yc
(25)
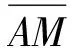
5 ψ、φ、θ以及P点、C点坐标与油缸铰链点之间关系
参照图1,在三角形OAM中应用余弦定理得
(26)
应用正弦定理有
(27)
闸门与底面夹角:
ψ=α+θ-β
(28)
P点坐标:
(29)
C点坐标:由于下游水位是设计给定的,且保持衡定,变化的只有下游液面与闸门交线投影即C点横坐标,该点坐标很容易确定,只要将下游水位纵坐标值hc代入闸门投影直线方程y=tanψx中的纵坐标,便可得到相应的横坐标。
(30)
至此,已完成底轴驱动式闸门模型的受力分析。有了以上计算公式,就可以求出闸门在任意位置所受荷载的大小,即油缸受力大小。同时可求出油缸与负载平衡时,油缸缸径和长度,得出油缸绞点的准确设计位置等。在实际的算例中,根据以上数学模型公式计算起来往往比较复杂。为此,可以通过计算机编制求解程序,快速、准确地求得相关结果,为底轴驱动式闸门的设计工作提供参考。
6 求解算例
在对底轴驱动式闸门的实际设计中,某一水利工程底轴驱动式闸门给定有关参数。闸门宽度b=40m,闸门高度Lm=1.8m,底轴半径r=0.305m,水比重γ=1t/m3,初始水头h0=0.3m,下游水位hc=1m,底轴中心与油缸固定支座连线长度oa=3.8681m,曲臂长度om=2.001m,油缸结构长度s0=2.185m,油缸行程s=2.83m,活塞杆与缸筒直径之比k=0,液压系统压力p=1041t/m2,闸门自重Wm=20t,油缸行程等分数目n=10,OA与水平面夹角α=21.4576°,曲臂OM与闸门中面夹角β=45°,底轴止水处垂向坐标yb=0.185。
根据算例已知的参数,运行根据数学模型编写的求解程序,得到输出结果见下表。

模型输出结果

续表
根据算例的输出结果,可以为算例的设计工作提供以下几点指导建议:
a.液压油缸缸径最小尺寸上限出现在闸门直立状态时。
b.底轴扭矩的最大值并非出现在闸门的直立状态,就该算例而言是闸门与水平面成69.5215°夹角状态。
c.得出闸门运行时油缸的最小缸径、长度等参数。在该算例中油缸缸径D[i]设计值应取D[i]值的最大值,即D[i]不小于0.208521m;油缸长度值取AM[i]的最大值,AM[i]最大为5.015m,即油缸长度最少为5.015m。
7 结 语
综上所述,根据底轴驱动式闸门的模型图,分析得出底轴驱动式闸门的详细受力情况,建立闸门受力的数学模型公式。通过编写计算机求解程序,可实现底轴驱动式闸门液压油缸缸径及长度的参数化设计,提高了底轴驱动式闸门的设计效率和精确性,为闸门的设计工作提供了重要依据。
参考文献
[1] 赵双双,谭文彪.底轴驱动下卧式钢闸门水力计算方法探讨[J].陕西水利,2017(3):147-149,154.
[2] 杨兆权,胡友安.支座沉降下的底轴驱动闸门静力数值分析[J].水利与建筑工程学报,2013(2):154-157.
[3] 李学荣,沈静,时爱祥,等.浅谈底轴驱动回转启闭式钢闸门技术要点及控制措施[J].江苏水利,2014(7):17-19.
[4] 陈洪涛.常见新型活动闸及闸门技术特点[J].江淮水利科技,2016(2):10,28.
[5] 徐强,饶英定,徐礼锋.底轴驱动翻板闸门在水闸工程中的应用[J].江西水利科技,2014(1):17-20.
[6] 卢新杰,石守津,韩晶,等.苏州河河口水闸底轴驱动式翻板闸门设计[J].水利水电科技进展,2007(S1):11-13,28.
