渗透数学史教育之微课程开发与应用的教学研究

2018-05-16赵智勇

文化创新比较研究 2018年8期

赵智勇

（教育教研信息中心，河南安阳 455000）

全日制义务教育《数学课程标准（修改稿）》中指出：“数学是人类文化的重要组成部分，数学素养是现代社会每一个公民应该具备的基本素养”[1]。张奠宙先生曾说过：“当数学文化的魅力真正渗入教材、到达课堂、溶入教学时，数学就会更加平易近人，数学教学就会通过文化层面让学生进一步理解数学、喜欢数学、热爱数学”[2]。因此，数学的教与学的过程应该成为文化的传播与交流的过程。

随着时代的发展和网络的普及，教育教学方式正在悄然发生着一些变化，微课程在中学数学教学中的应用越来越受到重视，下面是在实验学校教学班数学教学中进行的针对综合题教学 “利用微课程渗透和传播数学史料中所蕴含的数学思想方法”的教学实践及思考。

1 引入史料，开发微课

1.1 问题的引入

我国古代《九章算术》勾股章中有：“今有勾五步、股十二步，问:勾中容方几何?”[3]这个问题实质上就是：“已知直角三角形的三边长分别为5、12、13，求该直角三角形中内接正方形的边长。”问题包含两种情况（见图1）：

图1

刘徽为勾股容方的关系式提供了两个证明，一个是利用出入相补原理；另一个证明是利用相似三角形比率不变原理。

1.2 问题的延伸

这个问题在教学中是相似三角形的典型应用问题，图1中隐含着一个特殊的、应用广泛的相似模型——“三直角型”，以下图2中几种图形等都是其基本形态或变式图形：

图2

上述相似模型的本质用文字表述即为：当两个直角三角形的非对应锐角之和为90°时，这两个直角三角形相似。

2 引进教学，感受本质

本节课教学选题的主要对象是“河南中考2016年23题”，为了给学生解决与直角三角形有关的综合题问题提供启示和帮助，在实际教学中，我们首先引导学生先观看上述微课程，并针对收获进行了交流和适度引导。接着出示了下面的例题。

例 1：如图 3，在平面直角坐标系中，已知 D（2，0），E（2,1），将△ODE绕点O逆时针旋转α度得到△OD′E′，且，求点 D′、E′的坐标。

图3

图4

分析：在平面直角坐标系下，可利用平面直角坐标系两条坐标轴相互垂直的特征，过旋转后的直角顶点作平行于坐标轴的直线构造“三直角型”相似模型，列比例式解之。为此分别过点D′、E′作x轴、y轴的垂线（图 4），利用△OND′∽△D′ME′可求得

例 2：（河南中考2016年 23题）如图 5，直线 y=-交 x轴于点 A，交 y轴于点 C（0，4），抛物线 y=经过点 A，交 y轴于点 B（0，-2）。点 P为抛物线上一个动点，过点P作x轴的垂线PD，过点B作BD⊥PD于点D，连接PB，设点P的横坐标为m。

（1）求抛物线的解析式；

（2）当△BDP为等腰直角三角形时，求线段PD的长；

（3）如图 6，将△BDP绕点 B逆时针旋转，得到△BD′P′，且旋转角∠PBP′=∠OAC，当点 P 的对应点 P′落在坐标轴上时，请直接写出点P的坐标。

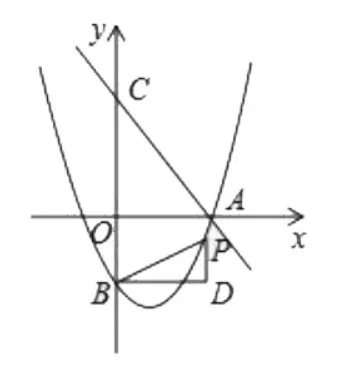
图5

图6

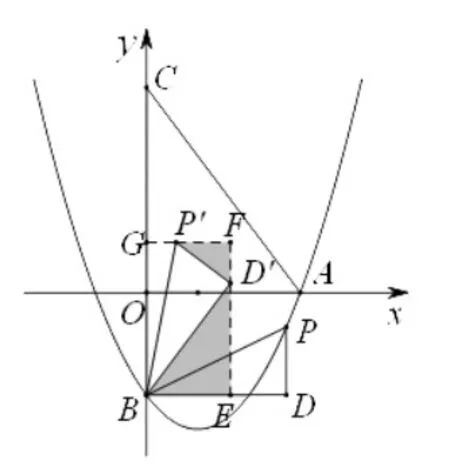
图7

此题第（3）问作为全卷的压轴，综合性强，共有三种情况符合题意，具有相当的难度。如果能表示出P′点的坐标，那么点P落在坐标轴上时，分别令P′点的横坐标和纵坐标为0，构造方程并解方程即可得到结果。

由于教学本题之前，学生观看了前面提到的微课程并进行了交流，又有了解决例1的经验，教学时通过启发学生联想微课程和例1，通过添加辅助线构造“三直角型”相似模型（如图 7）解答第（3）问。即设利用△BED′∽△D′FP′可得到用 m 表示的点P'的坐标分别令P'的横坐标和纵坐标为0，解方程即可得到5的坐标。这样顺利完成了本节课重点例题——例2的教学。

3 引导反思，总结收获

完成例题教学之后，教师和学生一起回顾本节课的教学，从数学文化、数学美和解题策略三个角度进行了教学小结，主要归纳了以下三点：

（1）品味数学史上问题的解决过程，对学习有启发和促进的作用。

（2）平面直角坐标系中涉及直角三角形旋转的问题，求点坐标时，可以过旋转后的直角三角形顶点作平行于坐标轴的直线，构造“三直角型”相似模型，“将不规则图形变为规则图形，或将分散的条件集中在一起，以便挖掘隐含条件，使问题得以解决”[4]。

（3）“三直角型”相似模型反映的是数学客观规律，其形态优美，应用广泛，构造和利用“三直角型”相似模型，列含有未知数的比例式计算相关线段的长度，往往简捷、快速。

4 承载文化，培育素养

数学承载着思想和文化，是人类文明的重要组成部分[5]。通过微课程渗透数学史教育，让学生在观看微课程的同时，经历解决问题的过程，感悟数学史料中蕴含的解决问题的思路和方法，并通过具体实例加以巩固，既渗透了数学文化，增强了学生学习数学的兴趣，又有利于提高探究能力。课后的调查问卷显示78.1%的学生认为引入数学史的微课程对数学学习很有帮助，20.5%的学生认为对数学学习比较有帮助；几乎所有的学生都希望老师在教学中使用数学史内容，其中期望课堂上讲授数学家故事、数学游戏、经典数学名题、数学知识的发展历史的学生分别占63%、68.5%、48.2%、64.4%。