局域表面等离子体增强锗的光电响应特性

齐功民, 狄增峰, 任 伟

已有研究表明,贵金属纳米颗粒(如银、金和铜)因其量子尺寸效应和表面效应而表现出与体材料不同的特性[1-2],局域表面等离子体共振(local surface plasmon resonance,LSPR)特性就是其中之一.LSPR是金属纳米颗粒表面自由电子集体振荡与入射光子形成的耦合作用.由于在共振波长下,场强在金属与介质界面迅速衰减,因此不同于体材料,LSPR只能局域在金属纳米颗粒表面,无法传播.而由表面电子振荡与光子振动形成的共振,使得局域场强非常强,且共振频率主要受金属的电子密度、有效电子质量、颗粒尺寸、形状和周围介质的影响[3-7],因此很多独特的光学性质可以通过改变颗粒尺寸、周围的介质以及结构来实现.这一特性在光电子领域有重要的研究意义.

随着纳米技术的发展,LSPR的局域场增强效应得到了广泛的应用,比如用来实现表面拉曼信号增强[8]、提高太阳能电池效率[9-11]、改善传感器的灵敏度[12]、生物检测以及细胞标记等[13-14],而这些应用均对光的频率比较敏感.因此,通过改变影响金属纳米颗粒LSPR的因素,实现对频率的调控已成为研究的重点.已有很多的研究通过实验、理论和数值模拟致力于实现对频率的调控.比如文献[6-7,15]利用离散偶极近似(discrete dipole approximation,DDA)数值模拟和实验的方法研究了(金/银)纳米球、三角棱柱以及纳米壳不同形状的频率响应;文献[16]从理论上提出了基于共形和非共形变换的新方法来研究两个纳米颗粒的相互作用;文献[17]研究了LSPR在天线领域的应用.

锗作为微电子领域重要的半导体材料,相对于硅来说有更高的载流子迁移率和更小的禁带宽度,因此甚至有可能取代硅成为微电子行业的主流.把LSPR应用在锗上,可以有效地结合二者的优势,带来一些新奇的应用,比如可以增强锗基光电探测器的灵敏度或者锗的发光效率.在太阳能电池领域,银纳米颗粒经常被用来增强能量转换效率[18],或是增强发光[19-20].因此,研究LSPR在锗中的光响应特性,对构造锗基光电器件具有十分重要的指导意义.

本工作主要研究了1,2,3个银纳米颗粒在锗中的LSPR光电响应特性(研究2,3个颗粒情形是考虑到了实验的不可控性),并计算了其消光截面,考虑了偏振以及银纳米颗粒之间的距离(即银纳米颗粒密度)对消光光谱的影响.本工作从理论上发现,加入银纳米颗粒可以在可见光与近红外波段有效增强锗的消光响应,并在近红外波段出现新的峰位,同时通过改变光源的偏振方向和银纳米颗粒之间的间距,调控增强锗消光响应的频率范围.这一结果大大拓宽了锗在光电子领域的应用范围.

1 研究方法以及模型

锗的光电响应过程是光子将能量传递给电子使其成为自由电子的过程.光电响应的效率是内量子以及外量子效率共同作用的结果.利用局域表面等离子体的局域场增强效应,可以有效地使金属纳米颗粒附近的光子参与锗的光电转换,从而提高外量子效率.因此,通过研究嵌入银纳米颗粒的锗的消光光谱(光的吸收和散射,两种过程都与电子有能量的交换),可以有效地反映锗的光电响应特性.本研究用时域有限差分(fi nite difference time domain,FDTD)法来模拟计算消光光谱.

FDTD法是由Yee[21]在1996年提出的,现已被广泛用来指导实验.在通常情况下,FDTD法是把Maxwell方程式在时间和空间领域上进行差分化,利用蛙跳式算法(leap frog algorithm,即空间领域上的电场和磁场进行交替计算),通过时间领域上的更新来模仿电磁场的变化,即在一个有限的计算空间内,去计算在时间领域上空间电场和磁场的分布.这种方法可以计算复杂形状结构的电磁场分布,而且得到的时域电磁场可以利用离散傅里叶变换(discrete Fourier transform,DFT)转换成频域响应,使用十分方便,被广泛应用于各个领域[22-26].

为了探究银纳米颗粒在锗中的基本LSPR消光特性,本工作利用银纳米球简化模型来进行计算.数值模拟模型如图1所示,其中银纳米颗粒嵌入在锗中,图示为xy截面,z轴垂直于纸面向外.本工作用r表示银纳米球的半径,用d表示球与球之间的距离,用k和E分别代表入射光的传播方向和电场的偏振方向,用M表示等边三角形的中心点.

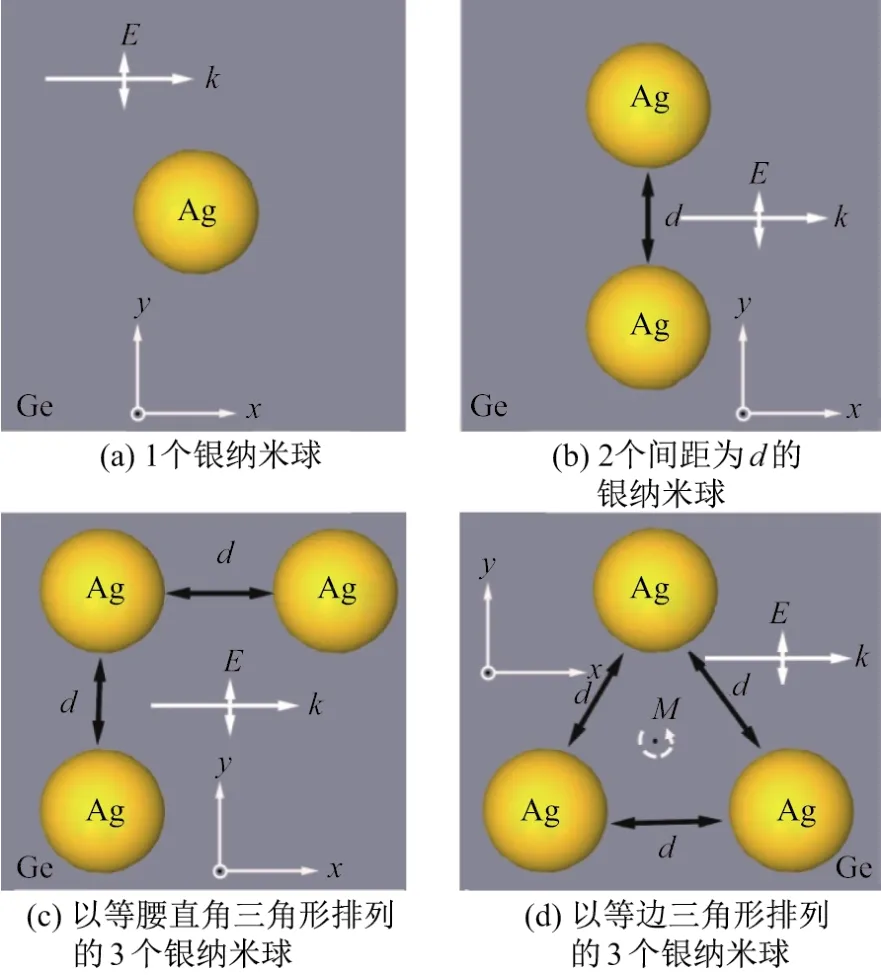
图1 xy截面数值模拟模型图Fig.1 xy-section for models

本工作用一个4 fs短脉冲平面波来激发银在锗中的LSPR,扫描波长范围为300∼1 800 nm.因为场主要局域在银纳米球附近,所以在距离银纳米球较近的位置(约50 nm)记录总场,在较远的位置记录散射场(去掉入射场).根据数值模拟得到的散射场和总场,利用如下公式推得其消光截面[27-28]:

式中,其中σabs(ω)为吸收截面,Pabs(ω)为被银纳米球吸收的总能量,σscat(ω)为散射截面,Pscat(ω)为总的散射能量,Isource为入射光强度.由式(1)可以看出,消光截面是由吸收和散射造成的.

2 结果与讨论

2.1 1个银纳米球在锗中的LSPR消光特性

本工作首先计算了单纯锗和1个银纳米球在锗中的消光特性.如图2(a)所示,银纳米球在空气中的消光响应非常弱.当锗中没有银纳米球时,其本征消光峰位在607 nm.当把半径r=10 nm的银纳米球放到锗中时,发现其消光响应整体增强,且在990 nm处出现了另一个峰位.第二个峰位处的电场分布如图2(a)中的插图所示,是典型的LSPR偶极振动模式.为了验证这是由LSPR引起的增强,本工作根据Mie理论和准静态近似理论[29]进行了证明.对于一个体积为V,介电常数ε=ε1+iε2的纳米球在介电常数为εm的均匀介质中,其消光截面可表示为

根据式(2),若要使消光截面达到峰值,就需要使(ε1+2εm)2取最小值,即[real(εAg)+2real(εGe)]2(其中real(·)代表取实部)取最小值.由锗和银的介电常数[30](见图2(b))可知,满足取最小值的位置在950 nm左右(即图2(b)中点A处).考虑到误差,这一结果很好地解释了上述现象.

图2 1个半径为10 nm的银纳米球在锗中和空气中的消光光谱(插图是偶极振动模式图),以及银和锗的介电常数实部Fig.2 Extinction cross section bands of a single Ag nanosphere in Ge with r=10 nm(the inset is the dipole mode),and the real part of dielectric constant of Ag and Ge

这种增强特性,可以提高锗在长波段的光电响应(在消光响应过程中,占主导的是吸收,吸收的光子激发电子成为自由电子).在光电领域,这种增强特性可以用来提高锗基光电探测器的灵敏度,也可以用来增强锗的发光.对于银纳米颗粒嵌入锗中的操作难点,本工作提供了一种可行的方案,即利用离子注入和退火的方法实现银纳米球的嵌入.因为银在锗中的溶解度很低,退火之后更容易聚集形成银纳米颗粒[31],而且还可以通过控制注入条件来实现对银纳米颗粒大小的调控.

根据Mie理论,当颗粒尺寸较小(2r≤20 nm)时,粒子可被近似认为处于同相位均匀电场中,表现为简单的偶极子共振模式[32].大一点的颗粒可以出现四极子、八极子或更高阶多极子振动模式.对此,本工作对银纳米球不同半径下的消光光谱进行了研究,结果如图3所示.相比于r=10 nm的情形,更大半径的银纳米球峰位更杂乱.这也验证了Mie的理论,高阶极子模式开始显现.而波长在600 nm以下时,光谱响应峰形基本不变,说明在这个波段,起主要作用的是偶极模式.

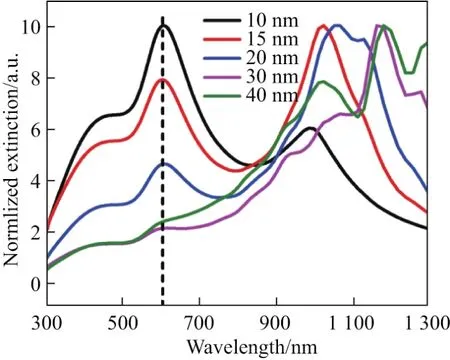
图3 在锗中,不同半径的1个银纳米球的消光光谱Fig.3 Extinction cross sections of a single Ag nanosphere in Ge with different radii

2.2 偏振、间距对2个和3个银纳米球在锗中的LSPR消光特性的影响

对于1个银纳米球,因其对称性比较高,光源的偏振不论在哪个方向都是等价的,因此偏振对1个银纳米球的消光特性没有影响.但是对于2个银纳米球,沿着两球心连线的偏振(y偏振)和垂直于两球心连线的偏振(z偏振)是不等价的.因此,本工作对这种情况进行了探索,结果如图4所示.可以发现,y偏振在更宽的光谱范围内都有较强的消光响应.可以这样设想,当入射光的偏振方向与两球心连线平行时,激发的LSPR在球心连线方向振动(见图4右插图),那么两球之间就会产生耦合振动,且由于共振排斥作用[33],其中一个耦合振动的峰位会红移出现在长波长区域,导致在更宽的光谱范围内有较强的消光响应.相反,当入射光的偏振方向与两球心连线垂直时,两球的LSPR共振方向平行(见图4左插图),且相距一段距离,耦合就没那么强,其效果和1个银纳米球的结果类似.

图4 在锗中,2个半径为10 nm、间距为2 nm的银纳米球在z和y偏振下的消光光谱(插图为在z和y偏振下的第二个峰位处电场分布)Fig.4 Extinction cross sections of two Ag nanospheres with r=10 nm,d=2 nm in Ge for z and y polarization(the insets are electric profi les for the modes in the second peak positions with z and y polarized incident light,respectively)

在y偏振下,本工作研究了2个银纳米球之间的距离d对LSPR的影响(即银纳米颗粒密度的影响),结果如图5所示.可以发现:当两球距离较近(即耦合比较强)时,其共振峰位在长波长区域;距离较远(即耦合比较弱)时,共振峰位慢慢向短波长方向移动;当距离达到20 nm时,共振峰位几乎和1个银纳米球的共振峰位在同一个位置(即球与球之间的相互作用消失了,退化为1个球的情形).这个现象验证了之前的猜想:距离越近(密度越大),耦合越强,共振排斥作用越大,峰位红移;距离越远(密度较小),排斥作用减弱,共振峰位红移现象不明显.因此可以据此来控制LSPR,从而达到调控光谱响应范围的目的,实现更广泛的应用.

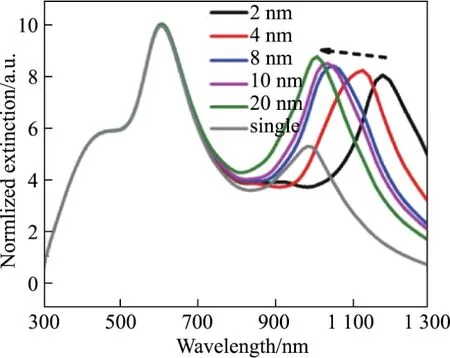
图5 在锗中,2个半径为10 nm、不同间距d的银纳米球在y偏振下的消光光谱Fig.5 Extinction cross sections of two Ag nanospheres with r=10 nm in Ge for y polarization for different separation distances d

对于3个银纳米球的情形,本工作同样研究了偏振以及球间距对LSPR的影响,结果如图6所示.对比图6(a)中两种偏振结果,y偏振在更宽的光谱范围内也有较高的光响应,耦合同样出现,且在1 500 nm的位置出现一个共振峰位.这与图4和5中2个银纳米球的情形类似.从图6(b)和(c)也可以看出,随着银纳米球间距的增大(即耦合减弱),共振峰位也向短波方向移动,有接近1个银纳米球情形的趋势.对比等腰直角三角形、等边三角形两种情形以及等边三角形不同转角情形(见图6(d)和图7),消光响应差别不大.这说明在y偏振下,耦合差别不大,消光特性对于银纳米球的相对位置没有太大的依赖性.这一结果有助于减少实验的控制因素,更有利于实验目的的实现.

2.3 消光频率调控的主要影响因素

对比图1(b)∼(d)3种情况的计算结果可知,消光光谱依赖于偏振和球间距,但对球的摆放位置无明显响应.在y偏振下,所有情况都对球间距有明显响应,但对球的相对摆放位置不敏感.而球间距的大小在实际情况中代表了特定大小的锗区域内银纳米颗粒的密度.因此,可以在实验中通过调控银离子注入来控制银纳米颗粒的密度,从而实现对消光响应频率范围的控制.

在实验中对于颗粒间距的控制却不太容易,且存在间距大小不一的情况,但这恰恰能够保证在大的范围内实现很高的光响应增强.因为单一间距的纳米颗粒峰位是固定的,如果球间距不一致,那么就会在不同的频率下有峰位,使得在整个频率范围内都会有很高的消光响应.

综上可知,在半径不变的情况下,影响消光光谱的主要因素是球间距(即纳米颗粒的密度).

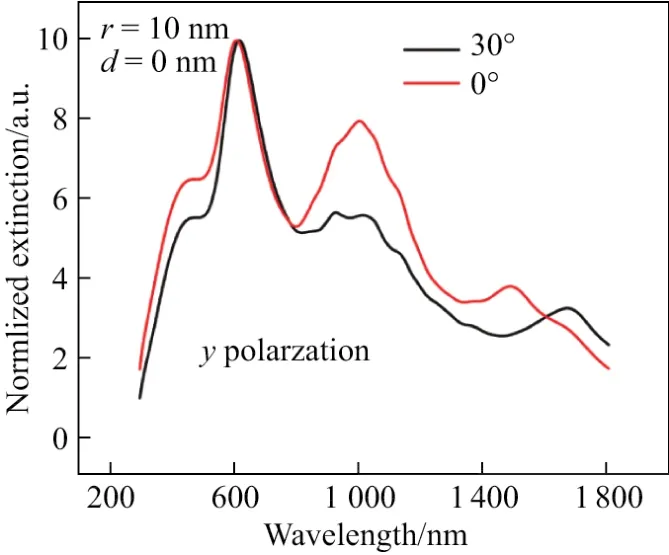
图7 在锗中,半径为10 nm的3个银纳米球在y偏振下绕等边三角形中心点M逆时针旋转0°和30°得到的消光光谱Fig.7 Extinction cross sections of three Ag nanospheres with r=10 nm in Ge for y polarization direction,counterclockwis rotating angles of 0° and 30° about the central point M

3 结束语

通过模拟计算1,2和3个银纳米球的消光光谱,得到如下发现:对于1个银纳米球,可以有效增强锗在可见光到近红外光谱范围内的消光系数,使得光谱响应范围更广、更灵敏;银纳米球的存在还在消光光谱上引入了新的共振峰,计算结果与Mie理论符合;对于2个和3个银纳米球情形,y偏振在更宽的光谱范围内都有较高LSPR光响应,而z偏振几乎与1个银纳米球的光响应类似;在y偏振下,球之间出现耦合现象,且共振峰位随着球间距的增大蓝移并逐渐退化为1个银纳米球的情形;消光特性与3个银纳米球的位置摆放关系不大,这有利于实验目的的实现.

根据上述发现可知,可以通过控制光源偏振方向、银纳米颗粒的个数以及球间距来实现增强锗的光响应频率范围的调控.在实际中,只要控制银纳米颗粒的密度,就会在很大的范围内实现光响应增强.这一发现,不仅可以促进锗在光电子领域的应用(比如锗基的传感器、发光器件),也对LSPR在光电领域的应用(比如高灵敏度的宽光谱测量器件,高效率的太阳能电池)有重要的参考价值.