双出口教室的人群疏散建模和模拟
2018-05-16董力耘蓝冬恺段晓茵
董力耘, 蓝冬恺, 段晓茵
近年来,大型群体活动或校园中的踩踏事故屡有发生,因此如何安全、快速地疏散人群受到越来越多的关注,其中一个典型的场景就是教室人群的疏散.许多学者都针对这种场景进行了实验或模拟研究[1-18].对于单出口的房间,主要研究人群在小出口处的成拱现象.对于多出口的房间,还涉及出口的选择问题.一旦某个出口发生拥堵,有些人可能转向另外一个虽远但较为通畅的出口.如何有效刻画疏散过程中行人动态选择出口的行为是模拟多出口人群疏散的关键.由于微观交通流模型可以细致刻画行人之间的相互作用,因此被众多国内外研究者用来研究人群的集体行为和自组织现象.典型的离散微观模型,如基于背景场的元胞自动机模型[2]和格子气模型[3],因其具有规则简单、易于高速数值模拟且适用于模拟复杂情况下的人群运动的优势而得到广泛的应用.在模拟多出口人群疏散时,有些学者分别考虑了房间内部结构、出口宽度或出口处拥挤程度的影响[6-8,11,13],有些学者同时考虑了其中2种因素的影响[9-10,12].本研究将同时考虑上述3种影响人群疏散的因素,重点关注人群在疏散过程中的出口选择行为.
1 模型
在已有的单出口教室人群疏散实验中,曾观察到行人因为前方发生拥堵而选择另外一条较远却更通畅的路径,因此必须考虑前方行人对于后方行人的影响[15].据此,本课题组已建立了一个考虑行人影响的动态背景场元胞自动机模型[18].在大多数基于背景场的模型中,仅考虑了静态的障碍物,用静态背景场来反映行人的影响.而本模型将行人当作可以移动的障碍物,使得原本反映障碍物影响的静态背景场由于人群的运动而发生改变,因此称之为动态背景场模型.值得说明的是,由于学生都明确知道出口的位置,因此本研究忽略了原始背景场模型反映行人之间跟随效应的动态场[2].本研究中的动态场是由于移动障碍物所导致静态场随时间的变化.本模型还将教室内的设施(静态障碍物)分为两类:①不可穿越(如讲台和课桌等),行人通常只能绕过这类障碍物而不能直接跨越;②可穿越(如椅子等),这类障碍物会造成行人运动的延误,但仍可跨过.这两类静态障碍物对于背景场的影响并不随时间而变化.
在研究双出口人群的疏散时,前、后2个出口都会形成各自的背景场,分别用F1和F2表示.行人通过比较所在位置处2个场的场值来确定向哪个出口运动.一旦确定了目标出口,行人就在该出口所形成的背景场作用下向出口处运动.行人的主运动方向即是当前格点周围4个近邻(即Von Neumann近邻)中场值最小的那个方向.如果近邻中有多个格点均为最小值,则随机选择其中的一个方向作为主运动方向.规定行人不可沿对角线方向运动.
当行人的主运动方向确定以后,则根据目标格点状态确定实际运动方向.如果目标格点为空,则实际运动方向就是行人的主运动方向.如果目标格点已被占据,则行人可向左或向右偏移.如果左右两侧格点均为空,则等概率选择一个方向为实际运动方向.如果一侧格点被占据而另一侧格点为空,则未被占据的格点的方向就是实际运动方向.如果左右两侧格点均被占据,则行人保持不动.
当行人的实际运动方向确定以后,就可以向目标格点运动.对于要进入同一目标格点的行人,本研究以等概率选择其中一人进入,同时还要求他们都满足r>pc,否则都不能进入目标格点,其中pc是冲突概率,反映的是行人之间由于礼让等原因造成的延误.此外当行人当前所在位置存在椅子时,假设当s<pd时才可向前运动,其中pd是延迟启动概率,反映的是椅子对行人运动造成的延误.这里的r和s都是[0,1]之间均匀分布的随机数.
本研究中行人运动采用并行更新方式.
2 模拟结果和讨论
本工作采用动态背景场模型来研究双出口教室的人群疏散问题.房间被离散为L×W个格子,其中L和W 分别为房间的长度和宽度,取26和12个格子,每个格子的大小为0.45 m×0.45 m.房间右边墙上有上、下两个出口,前出口宽度为w1,后出口宽度为w2.房间前部有一个讲台,大小为3×2个格子.如图1所示,教室内共有8排8列桌椅,一共可容纳64名学生.每个格子最多被一个学生或障碍物(桌椅、讲台)占据或者为空.前出口有一大一小两扇门,因此有3种不同宽度,即大、中、小出口分别对应3,2,1个格子,在图中用L,M和S表示;后出口仅有一扇门,宽度为2个格子.房间内桌椅一共有4种排列方式,分别有1,2,3和4个过道,与单出口疏散实验[15]中所给出的桌椅排列方式相同.考虑到前出口宽度和桌椅排列的不同组合,共有12种可能的布置,分别用“出口宽度+桌椅排列方式”的形式表示,如前出口为小出口、第4种桌椅排列方式,则用S4表示.

图1 双出口教室示意图Fig.1 Sketch of the classroom with two exits
本研究根据单出口疏散实验[15]的结果,将行人步速设为1.50 m/s,略大于正常步速.在生成背景场时,椅子对场的影响系数为α,而行人的影响系数为β.为简单起见,假设行人的影响是椅子的两倍,即β=2α,且令α=1.此外还进一步假设延迟启动概率pd=0.4,冲突概率pc=0.5.采用上述参数,可以得到与单出口疏散实验符合较好的模拟结果.模拟时对每种情况都计算100次.每次模拟所得到的平均疏散时间定义为所有人疏散时间的算术平均值,而最长疏散时间则是最后一人离开房间所需时间的算术平均值.
图2给出了S4情况下,教室内人群疏散过程中不同时步的斑图,其中一个时步对应的物理时间为0.3 s.初始时刻,教室内坐满学生,如图1(d)所示.每个时刻,学生都会根据上、下两个出口所产生的背景场值大小选择自己的目标出口.在某格点产生的背景场值较小的出口表明学生离该出口较近.由于前出口产生的背景场F1在前排的值要小于后出口,因此前排的学生倾向于选择前出口.同理,后排的学生倾向于选择后出口.在模拟中发现,教室中间的少数学生会在中途改变目标出口,向相反的方向运动.值得说明的是,由于考虑了行人的影响,在背景场的作用下,学生在初始时刻倾向于进入就近的过道,而不一定是靠近出口的那一侧,这与实验观测结果是一致的.在疏散过程中,由于前后排的学生分别向前、后出口运动,选择2个出口的人数相近,因此与出口处的人群拥堵相比,距离仍是影响场强大小的主要因素.从图2(b),(c)中发现,有一名学生绕过讲台向前出口运动,选择了一条较长但较为通畅的路径.这种现象曾在单出口疏散实验[15]中观察到.由图2(c),(d)可见,由于前出口较小,有较多学生聚集在那里,而后出口较宽,学生可以较顺畅地疏散.一旦学生到达前出口附近,即使该出口已经较为拥堵,学生通常也不会选择距离自己较远但是比较通畅的后出口离开.这是因为前出口拥堵人群的影响尚不足以抵消到后出口距离的影响.如果增大系数β,即增加行人对拥堵的敏感度,可使拥堵出口上游的部分行人改变目标出口.
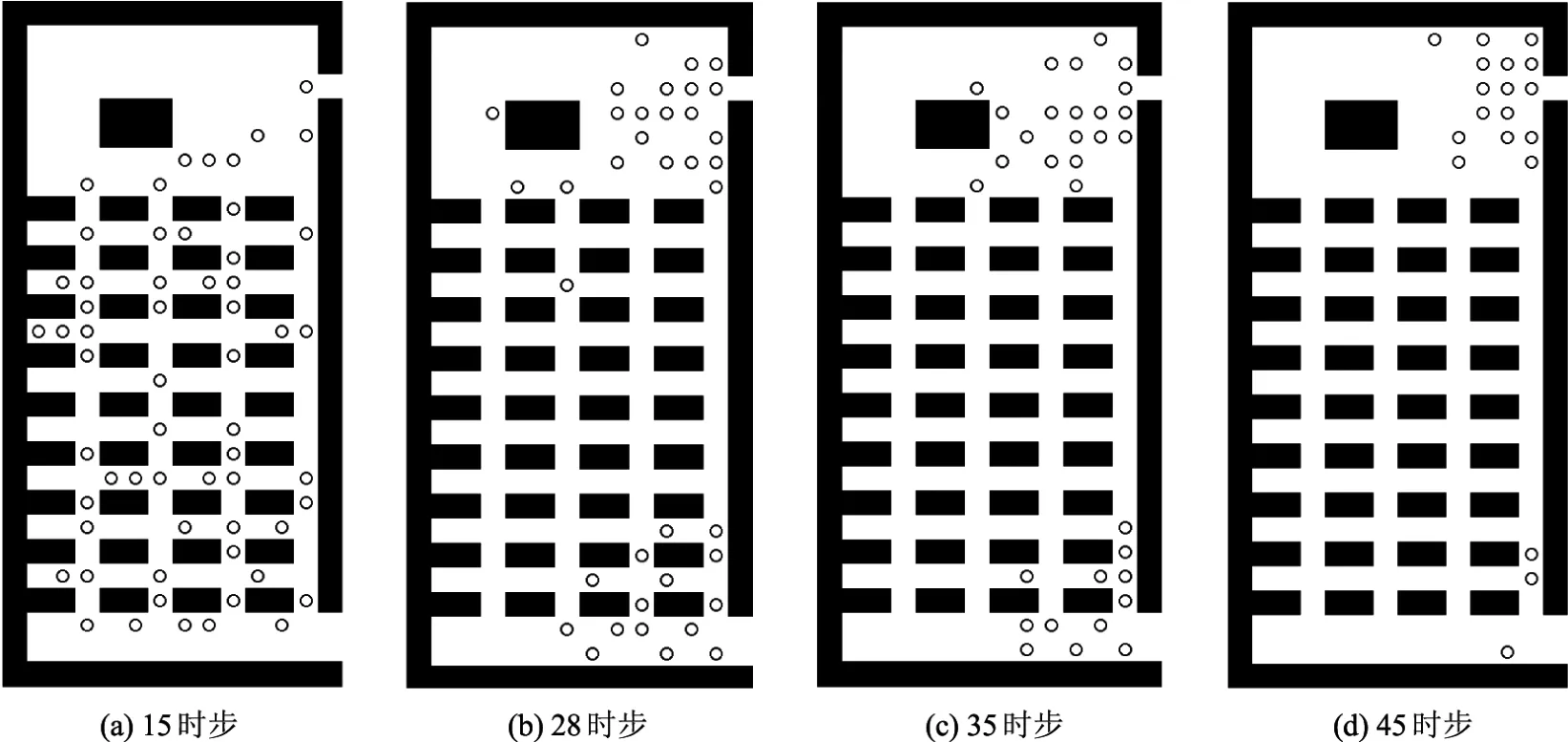
图2不同时步下典型人群疏散斑图Fig.2 Snapshots of a certain evacuation at different time steps
图3 给出了12种布置下,每个位置上学生疏散时间平均值的空间分布,其中第1列最靠近有窗的墙壁,第8列最靠近出口处的墙壁,第1排最接近讲台.结果表明,行人在不同位置的疏散时间反映了桌椅排列的特点.以第1种桌椅排列方式为例,疏散时间呈现明显的峡谷式分布,前后3排的疏散时间较短,而靠近墙壁的中间2排学生的疏散时间最长(见图3(a)~(c)).这与人们的日常经验是一致的.这种峡谷式的疏散时间分布在其他排列中也有所体现,如第2种桌椅排列方式(见图3(d)~(f)).对于1,2,3种桌椅排列方式,无论哪一排,靠近两侧墙壁的学生疏散时间最长.虽然第8列靠近出口,但是这一列的学生进入过道后往往被靠近出口的人群所阻挡,因此也不能很快地疏散.这与单出口疏散实验[15]的观测结果是一致的.
对于第4种桌椅排列方式,由于靠近出口墙壁有一条过道,因此第8列前、后2个座位的学生最靠近前、后出口,他们可以向右侧进入过道且与他人无冲突,因此他们的疏散时间最短.这是可以预期的结果.由于采用非对称排列结构,这种情况下的疏散时间分布具有与其他3种明显不同的特征.第1列学生的疏散时间相对于同排的学生而言是最长的.疏散时间呈现出明显的阶梯结构.一般而言,离出口越远,疏散时间就越长,而疏散时间最长的是位于教室中部第3~5排且靠近窗口的座位.
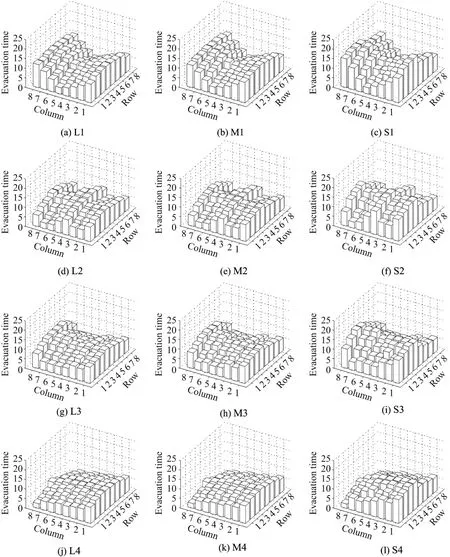
图3 12种布置下不同位置学生的疏散时间分布图Fig.3 Distributions of the evacuation time at each position under 12 different layouts
图4 给出了疏散时间与桌椅排列和出口宽度之间的定量关系.可以看出,平均疏散时间和最长疏散时间具有类似的性质,都随出口宽度和过道数量的增加而呈减少的趋势.值得说明的是,对于给定的过道数,存在多种桌椅排列方式,因此疏散时间也会有差异.在给定出口宽度时,疏散时间未必随过道数的增加而减少.由图4可见,小出口时的平均疏散时间比大、中出口时略长,而最长疏散时间则有明显增加.这是由于小出口时易出现较严重的拥堵,最后一个人从前出口离开的时间明显增加.在这种情况下,更多的人会选择从后出口离开,加上未发生拥堵前从前出口离开的人数,因而平均疏散时间的增加有限.
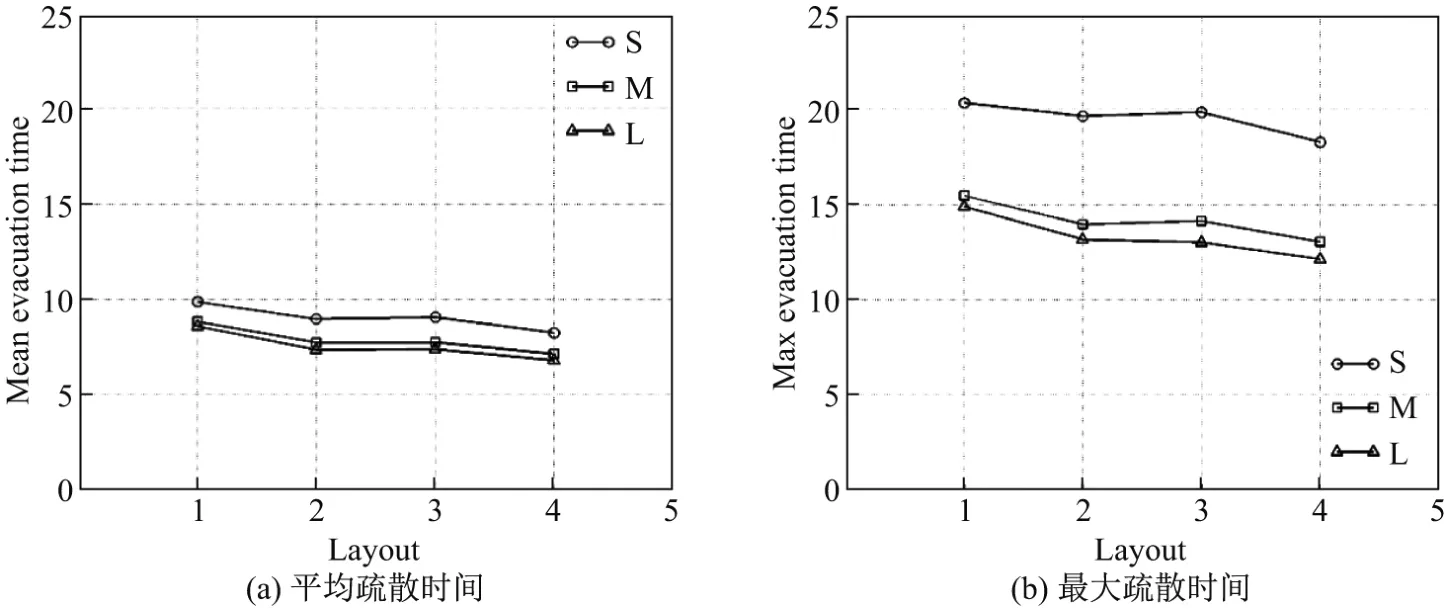
图4 不同出口宽度下平均疏散时间和最大疏散时间随排列的变化曲线Fig.4 Mean evacuation time and max evacuation time of different layout for different exit widths
对于同一种排列方式,疏散时间随着出口宽度的增加而减少,这是可以预期的结果.前出口增大时,教室出口的通行能力增加,疏散时间相对减少.对于同一种出口宽度,疏散时间随着过道数的增加而减少.对于第1种桌椅排列方式,仅有中间一个过道,且过道足够宽,同排的学生从两侧进入过道时,不会发生冲突.但同排学生每次最多只有2人可以同时进入过道,因此过道内的人流量较少,疏散时间较长.对于后3种桌椅排列方式,虽然过道数不同,但是同排学生可以同时进入过道的人数理论上都是4人.对于第2种桌椅排列方式,学生进入过道时没有直接的冲突,而对于第3种桌椅排列方式,除中间过道外,左右两个过道宽度仅为1,两侧行人进入通道时,会发生冲突,因而实际行人流量会有所降低.这就使得第2和3种桌椅排列方式的疏散时间接近.对于第4种桌椅排列方式,虽然左侧3个过道都会发生冲突,但右侧最靠近出口的过道却没有冲突,因此第8列的学生可以快速地离开教室,因而减少了对其他行人的影响.另外一方面,人群分散进入多个过道,在一定程度上减少了上游的集中来流,使得出口处不易形成严重的拥堵,因此疏散时间最短.
对于多出口疏散,一个重要的问题是确定人群选择不同出口的比例.图5给出了不同位置处学生选择前出口的概率分布.从整体上看,前3排学生都会选择前出口,而后3排学生则会选择后出口.介于中间的第4,5排的学生受前、后出口的影响大致相当.此时前、后出口处的拥挤程度会影响这2排行人的出口选择.进一步的统计分析表明,对于不同的桌椅排列方式,随着通道数的增加,选择后出口的人数会略有增多.与前3种桌椅排列方式相比,第4种排列方式中选择后出口的人数最多.对于同一种排列方式而言,当前出口为大出口时,选择后出口的人最少.总体而言,选择后出口的人数略多于前出口.这是由于教室前部有讲台而预留了较多空间,导致了第一排到前出口的距离比最后一排到后出口的距离更远.值得注意的是,在各种桌椅排列方式下,当前出口为中出口时,选择后出口的人数最多,而不是当前出口为小出口时.此外,当前出口为中出口时,从前出口疏散的人数要少于或者等于当前出口为小出口时的人数.这是因为出口所形成的背景场对教室内人群的影响主要取决于出口格点中最靠近人群的那个格点.小出口的位置相对于中出口来说更靠近学生,而前出口为大出口时最下面的那个出口格点就是当前出口为小出口时所在的格点.因此在本模型中,学生在选择出口时对距离很敏感.这一结论还要通过人群疏散实验来进行验证.

图5 12种布置下不同位置学生选择前出口概率分布图Fig.5 Distributions of the probabilities for student choosing the front exit at each position under 12 different layouts
3 结束语
本研究采用动态背景场元胞自动机模型研究了双出口教室内的人群疏散.学生通过比较前后2个出口在其当前所在位置处的场值来选择目标出口.由于考虑了行人作为移动障碍物的影响,学生在疏散时会倾向于进入最近的过道,并在疏散过程中根据前方的拥挤程度选择疏散路径和目标出口.模拟结果表明:距离是学生选择出口的主要因素,且学生对出口到其所在位置的距离很敏感.学生倾向于选择从最近的出口疏散,当学生到达该出口处,即使在该出口处已经形成了拥堵,学生也不会调转方向选择距离自己较远但是比较通畅的出口离开.由于教室里坐满了学生,因此选择前、后出口疏散的人数差别不大,出口处拥堵对于出口选择的影响有限.模拟结果反映了教室人群疏散的基本特征.对于一个更大的房间,当其中人数众多且分布不均匀时,出口处拥堵对出口选择行为的影响会更明显.本模型可以应用于研究一般情况下具有复杂内部结构、多出口房间的非均匀分布人群疏散.
