京津冀协同发展背景下“二孩政策”对京津冀人口规模及结构的影响研究

魏丽莹

（中国社会科学院金融研究所博士后科研流动站, 北京 100028; 中国信达资产管理股份有限公司, 北京 100031）

1 引言

人口结构变迁尤其是人口老龄化是全人类面临的重大问题。战后的二十世纪以人类的休养生息和人口的迅速增长为其重要特征, 而二十一世纪则以人类的不断进步和人口结构的重大转变或者说人口老龄化为其重要特征。未来几十年, 包括中国在内的大部分工业化国家将面临严重的人口老龄化的挑战。2010年我国人口普查数据显示60岁以上人口已占总人口的13.26%, 其中65岁及以上人口占总人口的8.87%。根据联合国人口预测数据, 2015-2045年60岁及以上人口占总人口的比例将年均增长16.55%, 也就是说, 未来30年我国将全面步入深度老龄化阶段。

京津冀协同发展政策起源于环渤海地区市长联席会的成立。2004年2月, 京津冀三地的发改委在国家发改委的召集之下, 召开京津冀区域经济发展战略研讨会, 达成“廊坊共识”。2008年2月, “第一次京津冀发改委区域工作联席会”在天津召开, 《北京市、天津市、河北省发改委建立“促进京津冀都市圈发展协调沟通机制”的意见》正式得到签署。2010年8月, 根据《京津冀都市圈区域规划》, 京津冀地区区域发展规划按照“8+2”的模式进行制订。2013年8月, 习近平提出了推动京津冀协同发展这一重要概念。2014年2月, 习近平主持召开了京津冀三地协同发展座谈会, 提出北京、天津、河北应打破“一亩三分地”的思维模式, 强调实现京津冀协同发展这一重大国家战略, 敦促首都经济圈一体化发展相关规划的制定; 同年8月, 京津冀协同发展领导小组成立。2015年4月, 习近平主持中共中央政治局会议, 审议通过了《京津冀协同发展规划纲要》。自此, 京津冀协同发展的概念开始深入人心。

京津冀协同发展战略旨在建立一条京津冀地区协同发展的路径, 该路径主要由产业、交通、环境、人口、服务以及创新等一体化政策构成。其中, 产业结构调整政策已实现初步计划; 交通、环境政策正在紧锣密鼓的制定当中;人口及公共服务政策已被提上日程; 京津冀地区的创新发展研究在不断的探索之中。京津冀协同发展战略已成为国家战略。京津冀税收一体化, 交通一体化, 通信一体化都在进行当中, 这为京津冀人口的定向流动和经济的协同发展创造了充足的条件。同时, 为了应对人口老龄化, 我国提出并实施了全面二孩政策。二孩政策实施可能对现有人口生育率产生重大影响, 对未来京津冀人口规模和结构产生重大影响, 进而对经济社会产生影响。彭希哲（2016）认为二孩政策对中国人口老龄化程度的减轻具有一定的作用, 但中国人口发展的长期趋势已经固化, 很难改变。陈友华（2016）认为全面二孩政策并非生育政策调整的终点,中国社会尚需更多的配套政策对其进行支持和完善。原新（2016）认为全面二孩政策的逐步完善对人口长期均衡发展和人口与经济社会、资源环境协调可持续发展具有积极意义。在京津冀协同发展战略实施的背景下, 科学合理地预测京津冀人口规模和老龄化变化趋势, 对京津冀未来经济社会发展和战略规划具有重要的参考意义, 如对京津冀的交通基础设施、教育等未来的规划等等。鉴于此, 本研究以京津冀协同发展作为控制条件, 充分考虑人口流动和区域一体化的影响, 利用最新的人口预测方法, 对“二孩政策”实施前后京津冀的人口规模及结构进行预测, 提出明确的人口发展趋势和政策建议。

2 人口预测模型和方法

人口结构预测根据时间和地域的不同会采用不同的方法, 中国常用的人口结构预测模型包括Leslie模型（张迎春,侯园园, 韩晓庆, 2014）、年龄移算法以及中国社会科学院王广州研究员开发的中国人口预测软件（CPPS）。

本研究利用组合生育模型、Kannisto模型以及灰色系统（Grey Model, GM （1,1））对年龄别生育率、年龄别死亡率进行分析及预测。其中组合生育模型属于归纳演绎模型的一种, 应用在年龄别生育率的研究上具有简便性和实用性, 经验证后, 与实际的年龄别生育率相差无几, 具有科学性; Kannisto模型是对老龄人口年龄别死亡率的预测模型, 同样属于归纳演绎模型, 通过与实际年龄别死亡率的对比, 可知其具有科学性; 灰色系统模型用来预测未来的年龄别生育率和死亡率, 是近年来较为流行的预测复杂系统发展趋势的模型, 简便、实用性强。

2.1 人口结构描述

根据《中国2010年人口普查资料》, 中国90岁以上人口占比为0.11%, 考虑到未来人口寿命变长的趋势, 本研究中假设最高寿命为90岁。因此, 在模型中的任一时间点上将会出现91个世代。根据《中华人民共和国劳动法》的规定, 法定劳动年龄指年满16周岁至退休年龄, 实际上,仅有2.23%的16-20岁人口属于经济活动人口。因此, 本研究假定人在0到20岁之间属于非经济活动人口, 21岁开始工作并成为独立的经济活动人口。根据《中华人民共和国婚姻法》的相关规定, 我国法定婚龄为男22岁, 女20岁, 且根据《中国2010年人口普查资料》, 仅有0.20%的人口由23岁之前或45岁之后的女性所生, 同时考虑到男性生育年龄的推迟, 本研究假定23岁到45岁之间为自然人的生育年龄, 只有在这一时间段之间自然人生育下一代,如此一来, 代理人的第一个孩子（第一部分的孩子）将在代理人43岁时离开家庭而最后一个孩子（最后一部分孩子）会在代理人65岁时离开家庭。同时假定代理人在68岁到90岁之间死去, 也就是说代理人在91岁时的死亡概率为1。代理人的生命周期如图1所示。

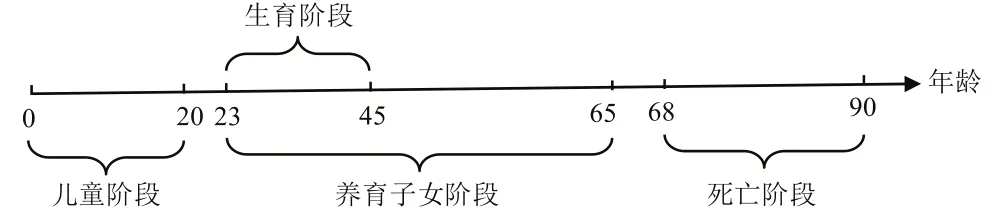
图1 模型中的代理人生命周期

2.2 人口发展方程

本研究中用N（a,t,k）表示特定时间点上某一阶层在某一年龄的人口总数,其中,a= 0,1,2,...,90, 表示代理人在t时刻的年龄,k= 1,2表示代理人的不同阶层。特定时间点上某一阶层某一年龄上的代理人子女总数用KID（a,t,k）表示,由于代理人在23岁以下时没有子女, 而在64岁以上时只有成年子女,所以当0≤ a ≤22和 65≤ a≤90时,KID（a,t,k）= 0。

本研究通过预测年龄别生育率和死亡率对人口年龄结构进行估算。以2010年作为基年进行考虑, 假设人口结构在50年之后达到稳定状态。在没有达到稳定状态之前,对于在2010年已经出生的人口和未出生的人口来说, 人口发展方程如下:

其中:

其中M （a）表示基年年龄别人口净迁移数量; Mshare（t,k）表示不同阶层流动人口占总流动人口的比例, Mscale（a,t）表示不同年份不同年龄的流动人口的规模, 当人口迁移制度不变时, 取值为1; d （a,t）表示年龄别死亡率, fr （a,t）表示年龄别生育率, Fshare （a,t）表示育龄年龄别女性占育龄年龄别总人口的比例。50年以后, 人口结构趋于稳定,人口自然增长率为0, 即0岁人口的数量与上一年相同, 流动人口的变化也与上一年相同。

2.3 年龄别生育率估算与预测

生育率反应育龄妇女的生育能力和生育水平, 一般分为总和生育率 （Total Fertility Rate, TFR）和年龄别生育率（Age Specific Fertility Rate, ASFR）。年龄别生育率指某一年龄（年龄段）育龄妇女在某一年的平均生育水平, 总和生育率指平均每一妇女在育龄生育孩子的总数。

生育率可以用生育率模型进行估计和预测, 生育率模型一般可分为演绎模型和归纳模型两大类。演绎模型从某些理论假设出发对生育率进行估计。例如: Easterlin 和Crimmins （1987）将诸多的生育率与经济、社会因素结合起来解释人口变迁, 并使用在人口调查中易于取得的中间变量对生育率的决定因素进行量化分析; Becker 和 Lewis （1973）的孩子数量质量转换模型将孩子的数量需求和质量需求与家庭收入联系起来, 并在后续模型中进一步发展（Becker &Barro, 1988; Barro & Becker, 1989）。归纳模型利用大量统计数据对人口的结构变化进行分析, 便于计算和仿真。

预测年龄别生育率和人口的结构变化, 首先需要对总和生育率进行预测。本研究以总和生育率作为观测序列,应用灰色模型（Grey Model, GM （1,1））进行预测。总和生育率数据来自《北京统计年鉴2005-2014》, 《天津统计年鉴2005-2014》, 《河北统计年鉴2005-2014》, 《北京市2010年人口普查资料（第六卷）》, 《北京市2000年人口普查资料（第六卷）》, 《天津市2010年人口普查资料（第六卷）》, 《天津市2000年人口普查资料（第六卷）》, 《河北省2010年人口普查资料（第六卷）》, 《河北省2010年人口普查资料（第六卷）》和中华人民共和国国家统计局网站。由于本研究主要研究内容不包括性别结构的变化, 因此为方便计算, 假设男女性别比例为1:1。

初始年龄别生育率数据来自《北京市2010年人口普查资料》第六卷, 《天津市2010年人口普查资料》第六卷和《河北省2010年人口普查资料》第六卷。由于统计数据上的不足, 只能得到间隔5年的年龄别生育率, 而无法直接获取15～49岁全部年龄上的生育率。为了弥补数据缺失, 本研究采用内插法和外推法对年龄别生育率进行估算。

本研究采用对数正态分布模型和泊松分布模型的加权组合模型对年龄别生育率进行模拟, 模型的数学表达式如下:

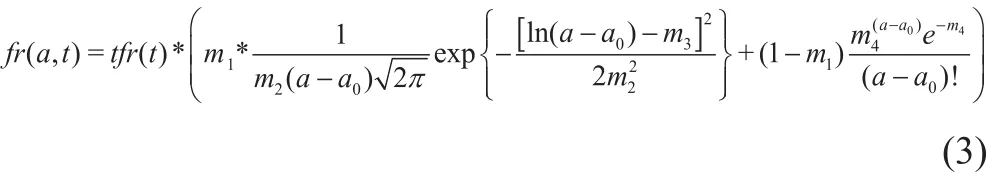
其中, fr （a,t）表示年龄别生育率, tfr （t）表示总和生育率, m1是对数正态分布函数在这一对数正态分布和泊松分布加权组合模型中的权值, a表示育龄妇女的年龄, a0表示初始生育年龄,根据人口普查数据, 令a0=14。

2.4 年龄别死亡率估算与预测

死亡率能够较好的反应一个国家和地区的人口总体健康状况。能够反应死亡率的指标包括粗死亡率, 年龄别死亡率, 婴儿死亡率等。粗死亡率（Crude Death Rate）是一种只对人口总数进行了标准化的指标, 它反映的是某年某地区平均每1000人中死亡的人数。年龄别死亡率（Age Specific Mortality）指某年度某年龄人口的死亡概率, 可以直接由统计数据获得。婴儿死亡率（Infant Mortality Rate）指婴儿出生后在达到1岁前死亡的概率。本研究选取年龄别死亡率这一指标对人口结构进行描述。

年龄别死亡率模型大致可分为两类。一类是函数模型,以年龄为自变量, 年龄别死亡率为因变量, 通过不同的模型设定和参数估计, 对年龄别死亡率进行拟合。另一类是实证模型, 这类模型也包含一定数量的参数, 这些参数是根据历史数据分析而设定的。

根据第六次人口普查资料, 本研究对2010年京津冀的年龄别死亡率进行分析及模拟, 数据来自《北京市2010年人口普查资料》, 《天津市2010年人口普查资料》, 《河北省2010年人口普查资料》。经研究发现, 在对中国的死亡率数据进行模拟中, 青少年时期Weibull模型的精度要高于Compertz模型, 在高龄期, Kannisto模型的拟合效果要好于其他模型。由于本研究仅考虑68岁至90岁之间的人口死亡率, 本研究将应用Kannisto模型对年龄别死亡率进行模拟。Kannisto模型如下所示:

其中, 68 ≤a≤ 90表示死亡年龄,d（a,0）表示2010年的年龄别死亡率。

年龄别死亡率的预测同年龄别生育率的预测类似, 将历史参数进行估计插值之后应用灰色模型对参数进行预测, 并由此来预测未来50年京津冀年龄别死亡率。

2.5 人口迁移分析

除出生和死亡外, 人口迁移是影响人口数量与结构变迁的另一大重要因素。人口迁移分析涉及到空间与时间两个维度的变化: 在空间变化的考察中, 人口迁移一般可分为国内迁移（Internal Migration）和国际迁移（International Migration）两种, 由于我国户籍制度比较严格, 在人口普查时一般也会考察省内迁移和省外迁移, 以及户籍在外乡镇、街道的外来人口数量; 时间维度主要考虑迁移人口年龄结构和居住时间等问题, 其中迁移人口年龄结构对人口结构变迁的预测具有重要意义。

人口迁移一般包括迁入人口（In-migration）, 迁出人口（Out-migration）, 总迁移人口（Gross Migration）, 净迁移人口（Net Migration）四个重要概念。其中总迁移人口是迁入人口与迁出人口之和, 而净迁移人口是迁入人口与迁出人口之差。

人口迁移模型多用来预测人口迁移总数或年龄别人口迁移。预测人口迁移总数的模型一般为实证模型, 包括只涉及到两地人口数目的Zips模型（Ho-Nam, 2007; Tarver &Mcleod, 1973）, 引入预期收入差异的Todaro模型（Todaro,1992）, Park （2007）引入劳动力转移的工资弹性模型等。严善平 （2007）建立了包含人均生产总值、经济增长率、非农就业增加率、城镇非国有部门职工比率、城镇登记失业率、省会之间的铁路里程和输入地与输出地之间存在的流动链等相关因素的实证模型, 对省际人口流动的机制进行研究。

拟合年龄别迁移模型多为函数模型, 包括拟合实际年龄别迁移率的Rogers模型（Rogers, 1976; Rogers & Castro,1982; Rogers, Raquillet, & Castro, 1978）, 以及在 Rogers模型的基础上衍生出来的其他模型（Raymer & Willekens,2008）, 我国的年龄别迁移率也可用Rogers模型进行拟合,但不同时期的迁移率拟合结果与实际数据有所出入。二元Logistic回归模型和多分类Logistics回归模型对年龄组别的总迁移以及户口迁移、临时迁移进行拟合, 结果显著。

净迁移人口的产生与收入的空间不均有关, 人们具有追求更高收入的迁移动机, 而幼儿也有跟随父母迁移的动机（Sjaastad, 1962）。本年的净迁移人口数据可由出生、死亡及年初、年末总人数数据间接得到:

本年净迁移人数=年末总人数−年初总人数−本年出生人数+本年死亡人数

但每年的迁入、迁出和总迁移人口数据无法直接得到,可以通过人口普查数据间接得到。根据《中国2010年人口普查资料》第七卷可得到全国按现住地和五年前常住地分的人口, 由此推算京津冀地区本年迁移人口估计值:

表1 2010年京津冀人口迁移数据

由表1可知, 北京和天津的净迁移为正数, 对外来移民具有较大的吸引力; 河北省的净迁移为负数, 人口处于净迁出状态; 其中, 北京迁入人口数目极高, 城市规模迅速膨胀, 这为整个城市的运行造成了一定的负担。

由于我国长久以来都有较严格的户籍制度, 假设在人口迁移政策不变的情况下, 人口按年龄有比例的迁移, 而每年的总迁移量不变。由于我国普查数据中迁移人口主要集中在0-64岁之间, 人口年龄别迁移模型可表示为:

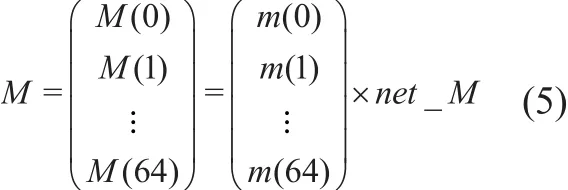
其中M(∙)表示年龄别净迁移人口数,m(∙)表示年龄别迁移比例, net_M表示净迁移人口总数。根据《北京市2010年人口普查资料》、《天津市2010年人口普查资料》以及《河北省2010年人口普查资料》中分年龄外来人口数可得到京津冀的年龄别迁移比例:

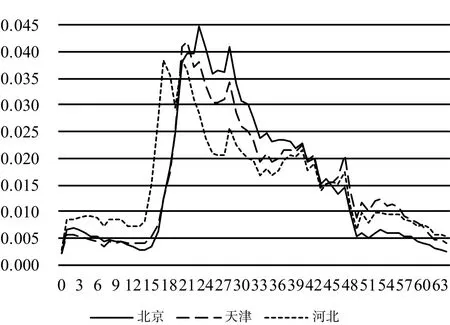
图2 2010年京津冀外来人口年龄别分布

如图2所示, 京津冀地区的外来人口年龄别分布基本相同, 均呈现两大高峰, 两小高峰和一低谷的趋势。其中一大高峰值在16-24岁之间, 反映了青少年外出求学或求职而带来的人口迁移; 另一大高峰在27-30岁之间, 主要反映了青壮年工作调动及外出务工从商所带来的人口迁移。一个小高峰位于幼年时期, 反映了外出务工从商人员携带幼年子女的迁移, 但这一比例远远小于16-30岁之间的迁移人口比例, 这造成了中国目前严重并值得关注的留守儿童问题; 另一个小高峰位于50-60岁之间, 即退休年龄, 这反映了一些老年人退休后迁回故乡、迁往气候或生活条件较好地区或者迁去与子女同住的社会现象。

图3 2010年京津冀年龄别净迁移人口(单位：百人)

根据式(5), 年龄别净迁移人口如图3所示。

由于假设了在人口户籍和迁移政策不变的情况下, 总迁移人口为常数, 则年龄别迁移人口也为常数, 并根据迁移人口的实际数目按比例进行调整, 这不仅符合我国人口迁移的现实状况, 也为人口结构的预测带来了方便。

3 人口结构预测及分析

3.1 基准情景下的人口结构预测及分析

Myrdal （1957）提出地理上的二元经济结构理论, 他认为在区域经济成长初期, 生产要素会首先集中在能获得较高收益的少数点地区上, 也就是说劳动力会由落后地区向发达地区流动, 即所谓的“回波效应”。这一效应使得发达地区越发的发达, 而落后地区越发的落后, 导致区域间经济发展水平差距扩大的后果。但当经济发展到一定程度以后, 发达地区的生产成本将会提高, 生产要素会向其周边扩散, 即产生“扩散效应”。Myrdal （1957）认为依靠市场的自发调节作用使得区域经济发展产生“扩散效应”并不符合发展中国家的实际情况。因此, 京津冀地区实行税收一体化, 交通一体化, 通信一体化为人口向京津周边辐射分布创造了充足的条件, 产业园区、环境保护和检验检疫的一体化进一步提前了“扩散效应”所产生的时间。

京津冀协同发展政策实施以后, 京津冀地区的人口仍旧会呈现向心型流动趋势, 但是核心会逐渐扩大, 由以北京为主转变为以沿海高速增长区域和次高速增长区域为主, 各中心城市为辅的格局。除此之外, 由于水资源短缺,北京地区于2015年宣布了新的人口上限, 到2020年, 北京市人口总量将被控制在2300万（张国, 2015）。清华大学教授蔡继明表示, 控制人口的主要方法将会是纾解非首都功能和调整产业结构（张国, 2015）, 因此假设从2016年起, 北京的净迁移人口会向北京周边即河北省转移, 以保证在2020年将北京人口控制在2300万以下。

假定京津冀协同发展政策实施以后, 京津冀地区的人口分布模式逐渐转变, 自2016年起, 京津地区的净流入人口减少, 并向京津周边即河北省扩散, 河北省的人口流动由省际流动为主变为省内流动为主, 实现人口的净流入。

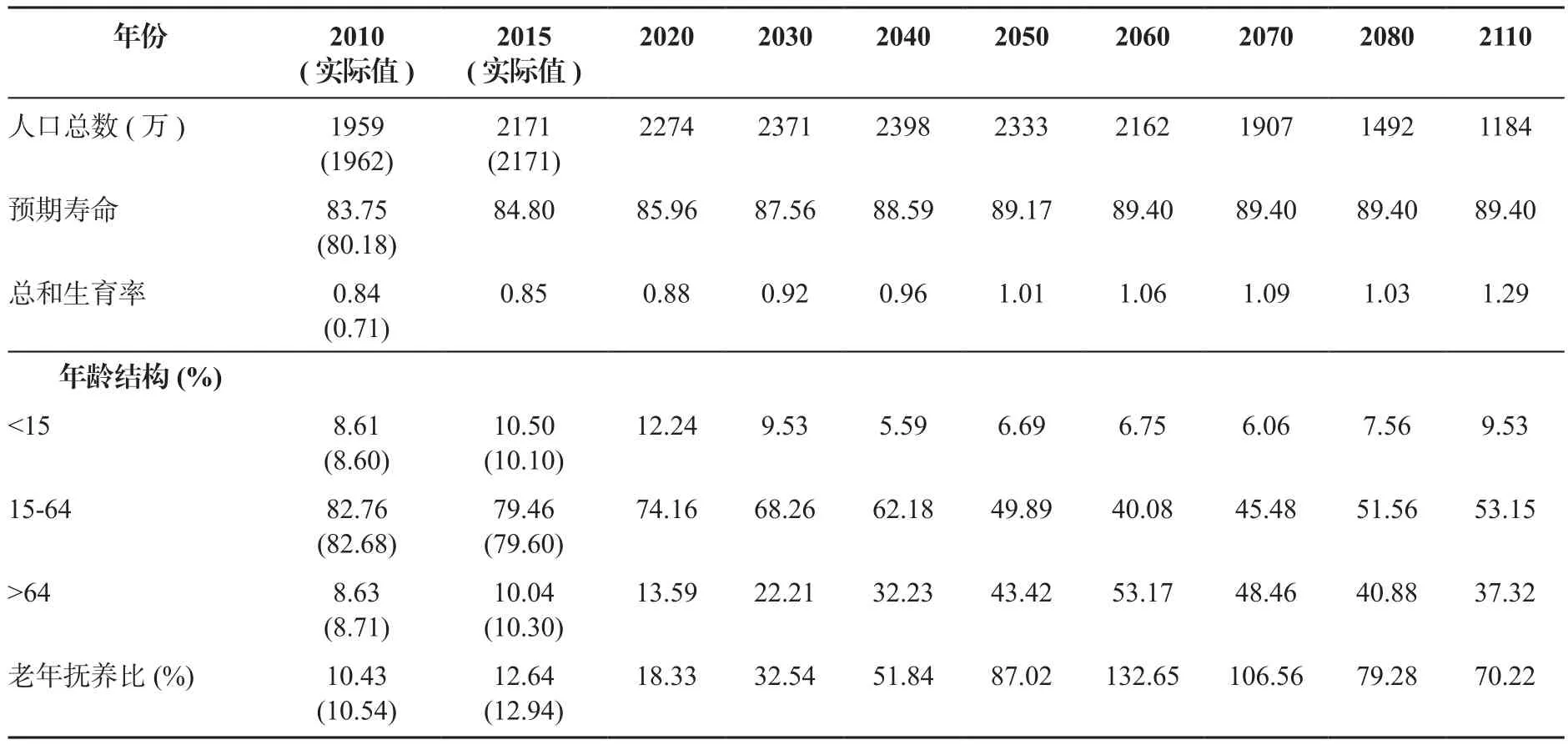
表2 北京人口结构预测2010-2110

表3 天津人口结构预测2010-2110

以2010年按年龄划分的常住人口数作为基年数据,利用年龄别生育率、年龄别死亡率以及年龄别人口迁移的预测值可以对京津冀的人口结构进行预测, 并根据2010-2015年之后的人口统计数据对模型进行修正, 以保证预测数据的合理性。预测使用软件Microsoft Visual Studio2015和Intel Parallel Studio XE 2016 Update 1, 预测结果如表2、表3和表4所示。

由人口预测数据可知, 京津冀地区人口总数在30年之内都保持稳定增长的态势, 由于过低的生育率, 北京在2050年之后人口总数开始有所下降, 而天津人口总数会在2070年后有所下降。由于人口迁移的影响, 河北省的人口总数会在2050年开始下降, 京津冀协同发展战略使得河北省的人口迁移呈现净迁入状态, 有效的缓解了河北省人口总数的下降趋势。

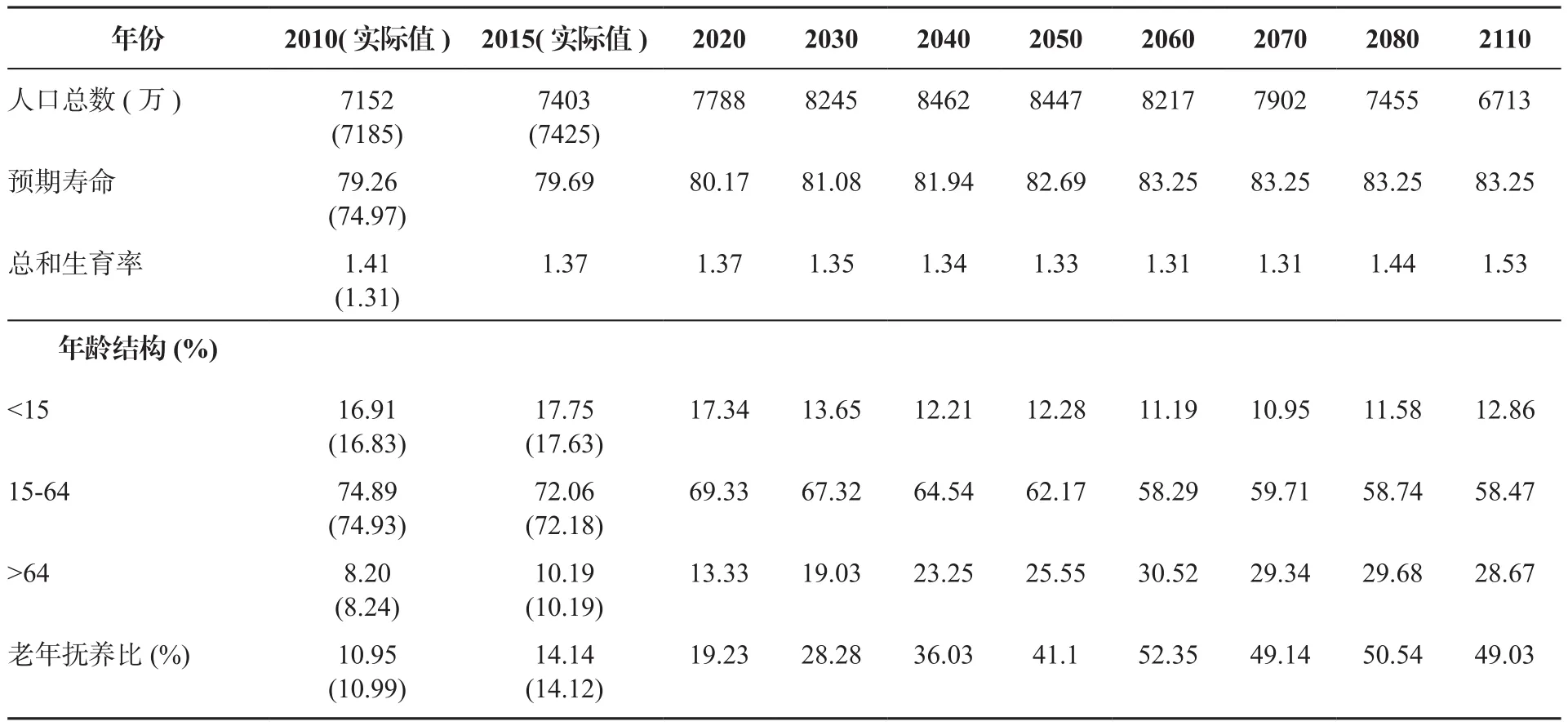
表4 河北省人口结构预测2010-2110

京津冀地区人口的预期寿命将会有显著的提高。北京市拥有最高的人口预期寿命, 这一数据在2060年之后将维持在89.40岁; 天津市人口的预期寿命在2060年之后将维持在87.71岁; 河北省人口预期寿命相对较低, 2060年之后将维持在83.25岁。人口预期寿命的显著提高是生活质量提升的标志, 但也会造成人口老龄化程度快速加深, 为社会经济生活带来诸多压力, 提出更多需求。

北京的总和生育率始终持续在较低的水平之上, 如果计划生育政策没有改变, 2050年之后有望达到每对夫妻生一个孩子的标准; 天津的总和生育率增长较快, 在2040年之后将保持在1.5以上; 而河北省的总和生育率变化较为平稳, 始终保持在1.31到1.53之间。较低的生育率虽然有效控制了人口增长, 但同样对人口老龄化的加剧起着推动作用。

《中国统计年鉴》中通常将15-64岁之间的人口作为劳动年龄人口, 0-14岁和65岁以上的人口作为被抚养的人口。现阶段我国处于15-64岁之间的劳动年龄人口处于74%以上, 居世界首位, 其中北京、天津的劳动年龄人口均达到80%以上, 这使得我国的经济具有很大的发展潜力,但这一数据正在持续下降。当60岁及以上老年人口占总人口的比例超过10%或者65岁及以上人口占总人口的比例超过7%时, 一个国家或者地区将进入人口老龄化社会。根据我国现有统计数据, 我国早已进入人口老龄化阶段,同时, 老龄人口的比例将持续快速增长, 预计在2060年达到顶峰, 然后会有所缓解。其中, 北京的人口老龄化程度最为严重, 在高峰期可达到50%以上。

人口抚养比包括总抚养比（Total Dependency Ratio）、老年抚养比（Aged Dependency Ratio）和少儿抚养比（Child Dependency Ratio）。“人口红利”是指当总抚养比低于53%时人口结构对经济增长具有的积极影响, 它来源于中国“中间大, 两头小”的人口年龄结构特点, 这种结构随着时间的推移而转变, 其中北京的“人口红利”期将持续35年以上, 而天津和河北的“人口红利”或将长期存在。

由于儿童在物质需求上远远少于成年人, 同样数量的老年人为经济带来的负担要远远高于儿童（Kleiman,1967）, 所以老年抚养比更加能反映一个国家或地区的人口负担规模。老年抚养比是指65岁以上人口占15-64岁劳动年龄人口的比重（Appave, 2009）。随着人口预期寿命的延长和计划生育时期出生人口的年龄增长, 我国老年抚养比将持续快速增长, 在2060年时将达到顶峰, 由于低生育率和低死亡率的存在, 北京的老年抚养比将达到132.65%,即使在生育率和死亡率相对较高的天津和河北, 老年抚养比也将分别达到71.64%和52.35%。这种严重的人口老龄化情况将为中国的社会和经济带来全方位的挑战。

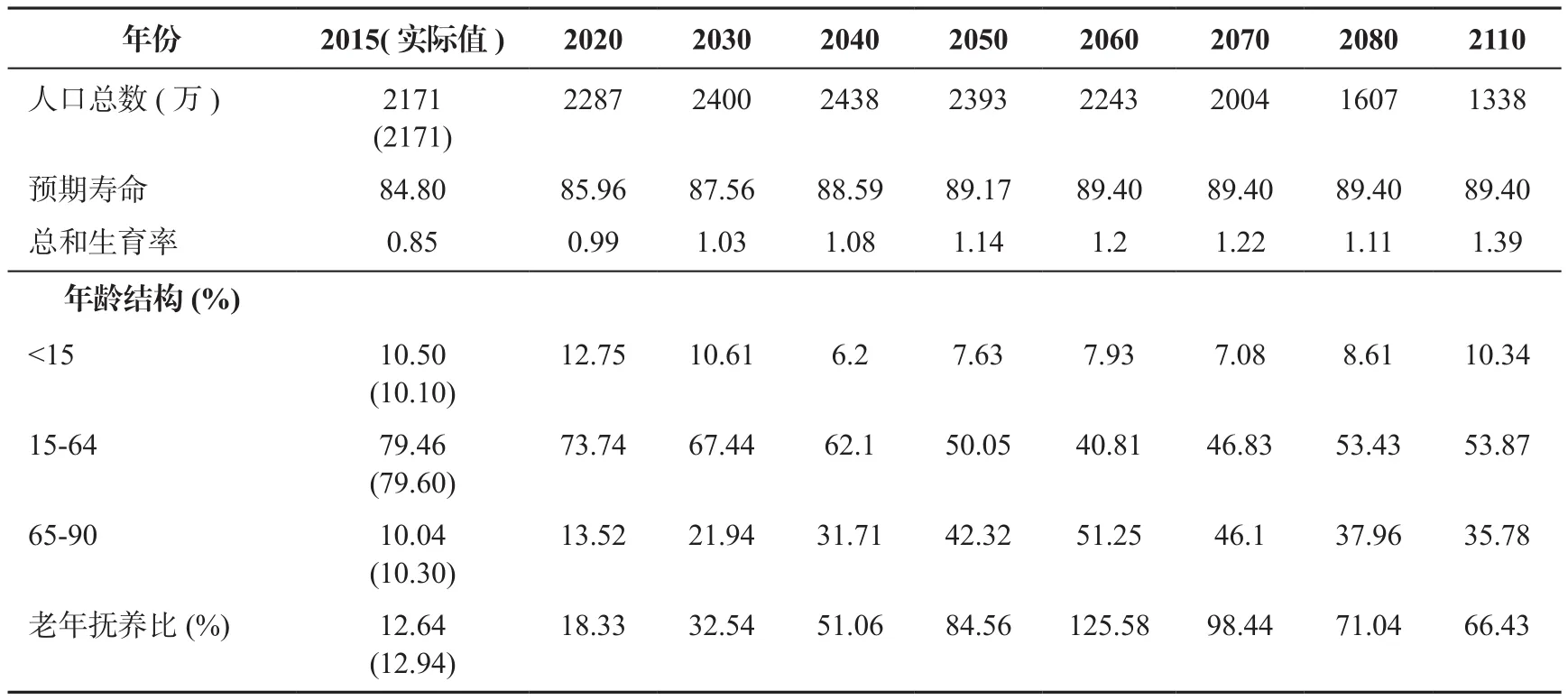
表5 全面二孩政策实施后的北京人口结构

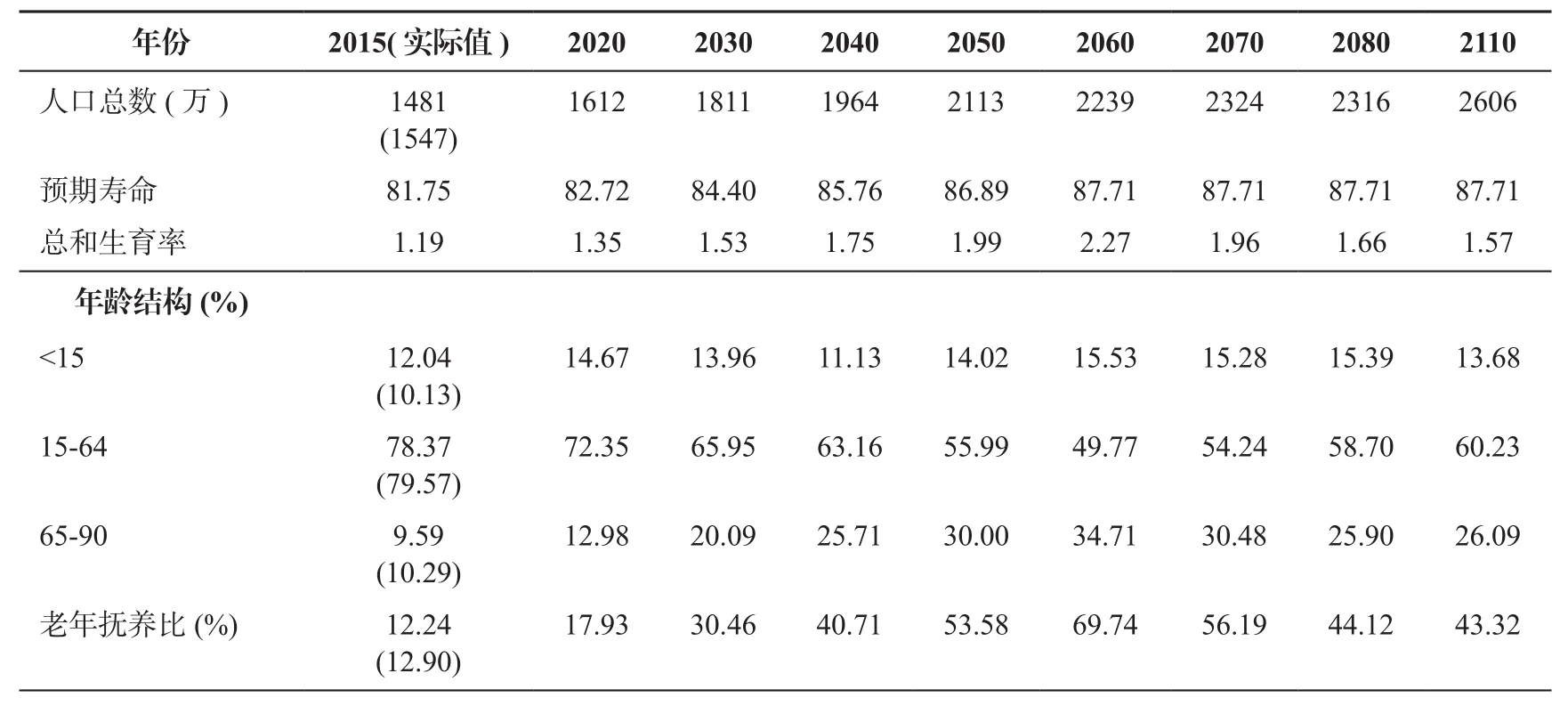
表6 全面二孩政策实施后的天津人口结构

3.2 全面放开二孩政策情景下的人口结构预测

随着我国人口老龄化程度的不断加深, 人口结构对经济增长的作用逐渐引起更多学者的关注, 而应对人口老龄化、促进经济发展的政策也开始逐步实施。2016年1月1日起, 全面二孩政策开始实施。从个人意愿层面来看, 二孩生育意愿不及预先设想（杨菊华, 2015）, 育龄人群意愿生育水平较低且保持稳定（张丽萍, 王广州, 2015）, 且人们更多的从自身养老和精神需求的角度做出二孩生育选择（张晓青, 黄彩虹, 张强, 陈双双, 范其鹏, 2016）。从社会层面来看, 人们是否选择生育二孩还取决于妇女劳动参与率与总和生育率之间的关系（蒙克, 2017）。

根据国家卫计委开展的专项调查显示, 39.6%的家庭有再生育打算。但根据单独二孩试行期间的数据显示, 仅有13%的育龄人口申请再生育（薛玲, 2015）。天津市社科院社会学研究所于2015年11月的抽样调查显示18.3%的人“打算生”, 还有17.7%的人“打算等等看”（李晶,2015）。根据河北省卫计委的数据显示: 在单独二孩政策的前期调研中, 有31.7%的符合条件的家庭表示有生育二孩的意愿, 而截至2015年8月仅有8.9%的家庭提出了生育二孩的申请（文西, 2015）。

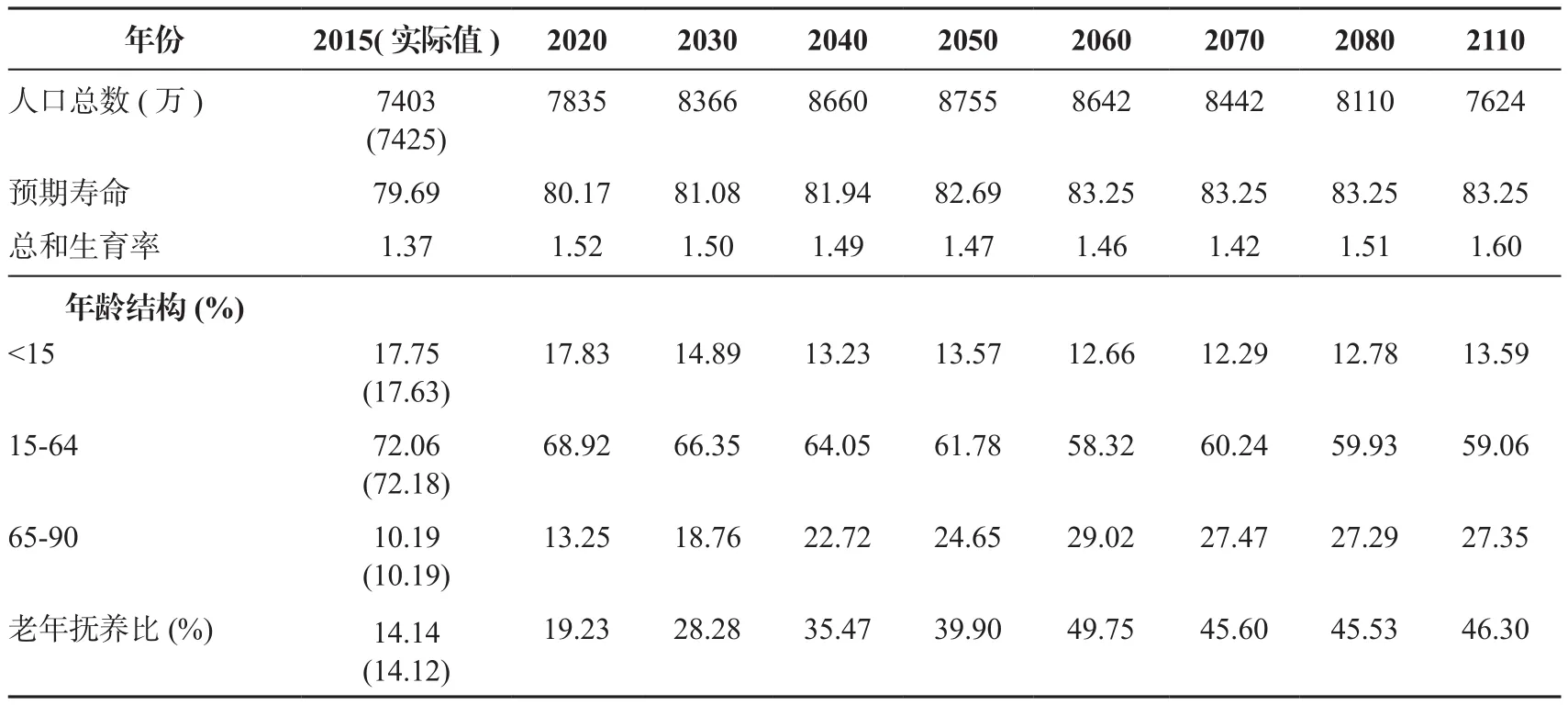
表7 全面二孩政策实施后的河北省人口结构

本研究假设2016年以后, 北京、天津以及河北原有的年龄别生育率分别提高到原来的1.13、1.06、1.11倍,由此可对全面放开二孩政策实施后的人口结构变迁进行模拟。全面二孩政策实施后的人口结构预测由表5、表6以及表7所示。

3.3 全面二孩政策对京津冀地区人口结构的影响

本研究分别对全面放开二孩政策后人口总数、工作年龄人口所占比例和老龄人口抚养比的变化进行分析。全面放开二孩政策对京津冀地区人口总数的影响如图4所示。

全面放开二孩政策实行后, 人口总数相对于基本情景来说开始逐渐增加, 增加幅度随着时间的推移会逐渐增大,到2080年止, 北京人口总数将增加7.7%, 天津人口总数增加4.5%, 河北省人口总数增加8.1%。由此可知, 全面放开二孩政策会在一定程度上增加人口总数, 减缓北京2040年之后人口快速减少的不利局面。

全面放开二孩政策对京津冀地区工作年龄人口所占比例的影响如图5所示。

全面放开二孩政策后, 工作年龄人口占总人口比例的总体变化趋势并没有改变, 但相对基准情景来说, 放开二孩政策使得工作年龄人口比例先是变得更小而后又变得更大, 变化幅度也经历了负向增大, 负向减小, 然后正向增大的过程, 这使得工作年龄人口占总人口比例的变化幅度增大。全面放开二孩政策实施后, 北京工作年龄人口所占比例在2045年之前低于基准情景, 2045年之后会高于基准情景, 但直到2060年之后才会逐渐增大; 天津、河北工作年龄人口占总人口比例在2060年之前都低于基准情景下的工作人口比例, 2060年之后随着工作年龄人口比例的上升才会逐步高于基准情景下的数值。

全面放开二孩政策对京津冀地区老龄人口抚养比的影响如图6所示。

全面放开二孩政策后, 老龄人口抚养比在2030年之前与基准情景相比没有变化, 2030年之后, 老龄人口抚养比将显著低于基准情景下的数据, 而且二者之间的差距会逐年迅速拉大, 人口老龄化状况有所改善。其中, 北京在2080年时老龄人口抚养比将降低8.2个百分点, 变化最为明显; 天津在2080年时老龄人口抚养比将降低2.4个百分点, 变化较小; 河北省的人口老龄化程度降低的比较明显,为5.0个百分点。

4 结论

全面放开二孩政策实行后, 京津冀人口结构产生了一系列重要的变化:

首先, 全面二孩政策实施后, 京津冀地区老龄人口抚养比在2030年之前与基准情景相比没有变化, 2030年之后, 老龄人口抚养比将显著低于基准情景下的数据, 而且二者之间的差距会逐年迅速拉大, 人口老龄化状况有所改善。北京在2020年成功将人口总数控制在2300万以下,但对老龄化程度并没有显著改善。同样, 天津也依旧面临着社会老龄化的压力。河北省由于工作年龄流动人口的大幅增加, 人口结构趋于合理化, “人口红利”将长期存在,河北省将更具发展潜力, 在京津冀协同发展中起到重要的作用。

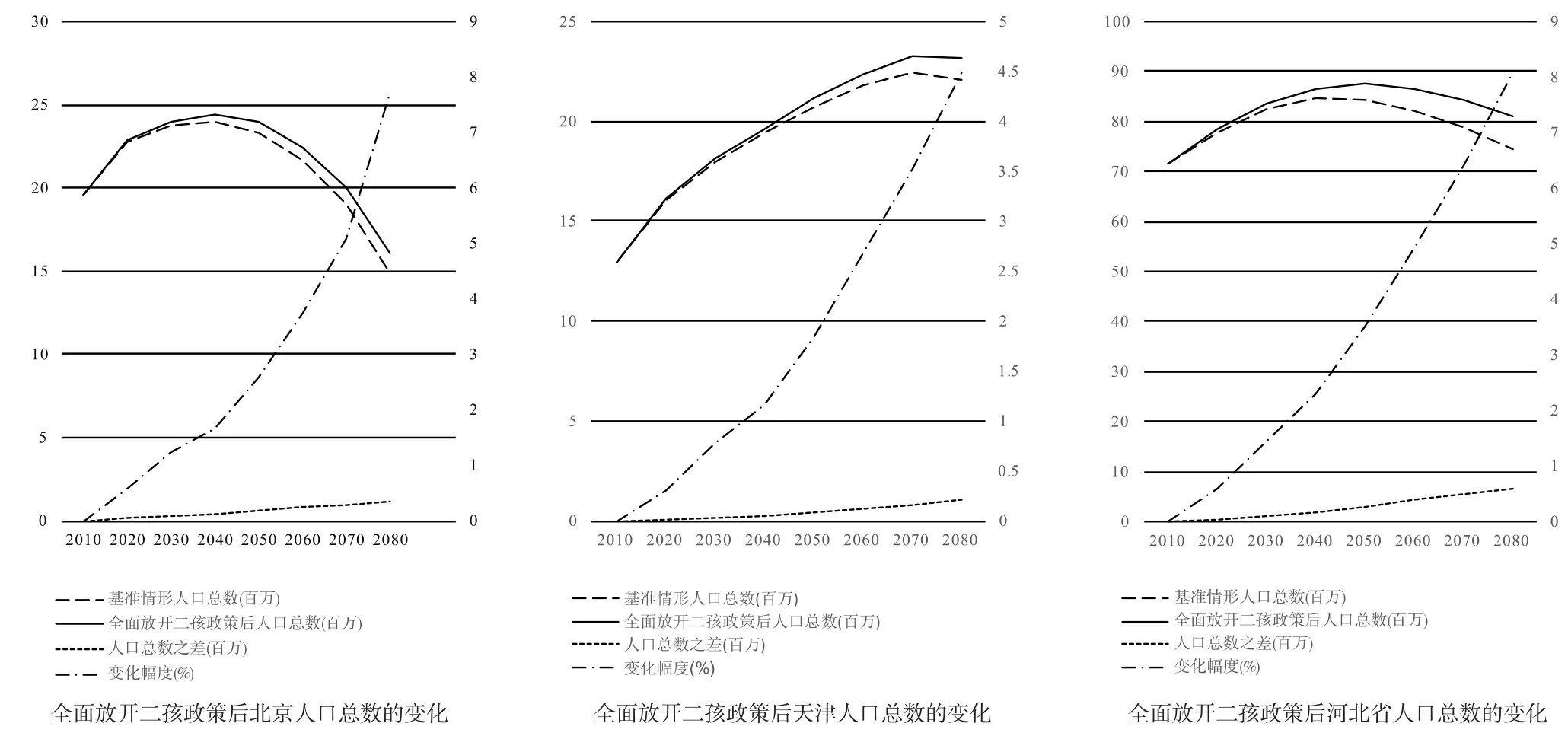
图4 全面放开二孩政策后京津冀人口总数的变化

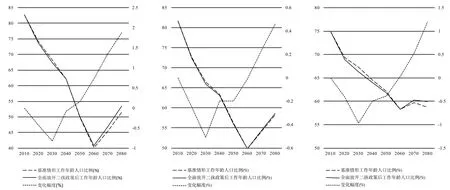
图5 全面放开二孩政策后京津冀工作年龄人口比例的变化

其次, 全面二孩政策实施后, 人口总数相对于基本情景来说开始逐渐增加, 增加幅度随着时间的推移会逐渐增大。全面放开二孩政策减缓了北京2040年之后人口快速减少的不利局面。同时, 工作年龄人口占总人口比例的总体变化趋势并没有改变, 但相对基准情景来说, 放开二孩政策使得工作年龄人口比例先是变得更小而后又变得更大, 变化幅度也经历了负向增大, 负向减小, 然后正向增大的过程。

最后, 由预测数据可知, 二孩政策放开后, 京津冀三地的人口结构变化存在显著差别, 京津冀协同发展战略在人口发展一体化方面并没有引起重视。

根据本研究的结论, 提出以下政策建议: 第一, 为应对人口老龄化对京津冀地区人口抚养比的负面影响, 政府应进一步促进全面二孩政策的推行, 继续大力鼓励夫妻生育二孩, 为人口结构的优化和经济的长期稳定发展奠定坚实的基础。第二, 在大刀阔斧的实行京津冀协同发展政策之时, 应更多的考虑到京津地区工作年龄人口相对减少的弊端, 提高人口控制目标, 吸引工作年龄人口的流入, 促进京津地区人口结构的优化, 稳固京津地区经济发展的成果。第三, 在制定京津冀协同发展政策之时, 将人口发展一体化目标融入整体协同发展架构之中, 进一步促进人口与区域经济的协同发展、和谐发展。

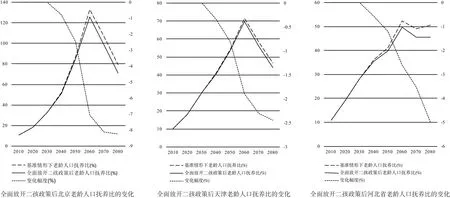
图6 全面放开二孩政策后京津冀老龄人口抚养比的变化

参考文献

1.陈友华. (2016). 全面二孩政策与中国人口趋势.学海,2016(1),62-66.

2.李晶. (2015, 2016). “二孩”时代生还是不生？天津双非家庭意愿最低,渤海早报.

3.蒙克. (2017). “就业—生育”关系转变和双薪型家庭政策的兴起——从发达国家经验看我国“二孩”时代家庭政策.社会学研究(5),218-241.

4.彭希哲. (2016). 实现全面二孩政策目标需要整体性的配套.探索(1), 71-74.

5.文西. (2015). 河北省卫计委就全面二孩放开政策表态, 全面落实中央政策.

6.薛玲. (2015). “全面二孩”来了, 你愿意生吗？新华报业网.

7. 严善平. (2007). 中国省际人口流动的机制研究.中国人口科学,1, 71-77.

8.杨菊华. (2015). 单独二孩政策下流动人口的生育意愿试析.中国人口科学(1), 89-96.

9.原新. (2016). 我国生育政策演进与人口均衡发展——从独生子女政策到全面二孩政策的思考.人口学刊, 38(5), 5-14.

10.张国. (2015, 2016). 北京再次宣布人口规模上限: 2300万,中国青年报.

11.张丽萍, 王广州. (2015). 中国育龄人群二孩生育意愿与生育计划研究.人口与经济(6), 43-51.

12.张晓青, 黄彩虹, 张强, 陈双双, 范其鹏. (2016).“单独二孩”与“全面二孩” 政策家庭生育意愿比较及启示.人口研究, 40(1), 87-97.

13.张迎春, 侯园园, 韩晓庆. (2014). “单独”二胎政策条件下人口年龄结构预测研究.经济统计学: 季刊,2, 135-146.

14. Appave, G. (2009). World migration 2008 : Managing labour mobility in the evolving global economy: Academic foundation.

15. Barro, R. J., & Becker, G. S. (1989). Fertility choice in a model of economic growth.Econometrica, 57(2), 481-501.

16. Becker, G. S., & Barro, R. J. (1988). A reformulation of the economic theory of fertility.Quarterly Journal of Economics, 103(1), 1-25.

17. Becker, G. S., & Lewis, H. G. (1973). On the interaction between the quantity and quality of children.Journal of Political Economy, 81(2),279-288.

18. Easterlin, R. A., & Crimmins, E. M. (1987). The fertility revolution:A supply-demand analysis.Bollettino Doculistica, 8(3), 531-533.

19. Ho-Nam, M. (2007). Zipf's Law under Migration. (Master of Philosophy), University of Hong Kong, Hong Kong.

20. Kleiman, E. (1967). A standardized dependency ratio.Demography, 4(2), 876-893.

21. Myrdal, G. (1957). Economic theory and underdeveloped regions.London: Gerald Duckworth.

22. Neupert, R. F. (1992). Population projections for Mongolia: 1989-2019.Asia-Pacific population journal / United Nations, 7(4), 61.

23. Park, S. (2007). Demographic changes and regional economy simulation result from the Chicago CGE model. (Doctor of Philosophy in Economics), University of Illinois at Urbana-Champain, Urbana.

24. Raymer, J., & Willekens, F. (2008). Applying model migration schedules to represent age-specific migration flows.Journal of Non-Crystalline Solids, 163(1), 90-96.

25. Rogers, A. (1976). Introduction to multiregional mathematical demography.Studies in Family Planning, 27(2), 405-406.

26. Rogers, A., & Castro, L. J. (1982). Model schedules in multistate demographic analysis: The case of migration.Multidimensional Mathematical Demography, 72,113-154.

27. Rogers, A., Raquillet, R., & Castro, L. J. (1978). Model migration schedules and their applications.Environment & Planning, 10(5), 475-502.

28. Sjaastad, L. A. (1962). The costs and returns of human migration.Journal of Political Economy, 70(5), 88-93.

29. Tarver, J. D., & Mcleod, R. D. (1973). A test and modification of zipf' shypothesis for predicting interstate migration.Demography, 10(2),259-275.

30. Todaro, M. P. (1992). Economics for a developing world: An introduction to principles, problems and policies for development (3 ed.).London: Longman.