货车整车质量辨识方法研究
2018-05-14贾天乐王洪亮彭湃薛冻
贾天乐 王洪亮 彭湃 薛冻


摘 要:针对货车整车质量辨识问题,分别对基于车辆纵向动力学和基于运动学的两种整车质量辨别方法进行仿真和实车试验研究。阐述了两种整车质量辨识方法的原理,在TruckSim软件平台上建立车辆模型并在多种工况下基于这两种方法进行仿真分析。根据仿真结果进行实车试验,提出了一种车速冗余计算和加速度计算的方法,利用带时变遗忘因子的递推最小二乘法(RLS)对实车质量进行估计。研究结果表明,所提出的车速冗余计算方法和加速度计算方法
准确有效,同时减少换挡次数能够显著提高辨识算法的收敛速度。相比于运动学整车质量辨识算法,基于车辆纵向动力学整车质量辨识算法能够有效地估计货车整车质量,鲁棒性好,估计准确,收敛速度快,具有很好的工程应用价值。
关键词:车辆工程;质量辨识;动力学方法;运动学方法;递归最小二乘法
中图分类号:U461.6 文献标志码:A
文章编号:1008-1542(2018)05-0394-07
近年来,汽车电子行业蓬勃发展,汽车质量辨识问题受到了越来越多科研人员的关注,其识别准确性直接影响到电控系统的控制精度。在坡道起步辅助系统(hill start assist, HSA)中,根据整车质量和所在路面坡度计算起步所需要的发动机转矩[1-3]。在电子驻车制动系统(electrical parking brake, EPB)中,地面制动力和整车质量相关,间接影响制动器的控制效果[4]。在车身电子稳定控制系统(electronic stability program,ESP)中,整车质量直接影响稳定性因数的大小,这将影响不足转向和过多转向的准确性判断[5]。此外,一些研究提出的减少重型车辆的燃油消耗控制算法与整车质量变化息息相关[6]。可见,汽车质量信息作为整车控制参数,对汽车智能化控制起到至关重要的作用,其辨识方法已经成为研究的热点。对于货车而言,由于装载货物前后整车质量变化较大,因此对货车载重量识别的研究有很大意义。
目前国内外很多文献是基于电驱动车辆对整车质量进行辨识[7-10]。利用电驱动车搭载的各种传感器设备,能够准确获得电机转矩、车辆的速度和加速度等信息。文献[11]提取这些信号的高频部分,将质量和坡度解耦,建立纵向动力学模型和运动学模型,借助递归最小二乘法得到了整车质量。文献[12]利用加速度分段的方法分别计算行驶阻力和整车质量,并在不同工况下验证算法的可靠性。文献[13]对4档AMT变速箱的纯电动物流车分别用递归最小二乘法和带遗忘因子递归最小二乘法进行整车质量辨识。总的来说,电动汽车质量辨识方法归结起来主要分为两大类:一是基于车辆纵向动力学模型的质量辨识,二是基于运动学模型的质量辨识。
在对内燃机车整车质量辨识方面,文献[14]将空气阻力和整车质量解耦,分别进行辨识,提出一种适用于空气阻力变化的整车质量辨识算法。文献[15]设计了车辆质量和道路坡度联合估计算法,其中利用了最小二乘辨识法和龙贝格(Luenberger)状态观测器。文獻[16]考虑不同参数的变化率对遗忘因子的影响,实现了时变等级和分段恒定质量的同时估计。内燃机车整车质量辨识方法比较单一,以车辆纵向动力学为主,且大都建立了复杂的模型,收敛时间偏长,工程化困难。
针对上述问题,本文对纵向动力学和运动学两种辨识方法在货车整车质量辨识问题上进行适用性研究,并提出相应的算法。在动力学软件TruckSim中进行多工况仿真分析,建立带遗忘因子的递归最小二乘法模型,根据仿真结果进行实车验证。
1 质量辨识方法分析
1.1 纵向动力学模型分析
由车辆纵向动力学公式(1)、驱动力公式(2)、加速阻力公式(3)、坡道阻力公式(4)、滚动阻力公式(5)和空气阻力公式(6),得到质量计算公式(7)。
当驱动力矩变化较大时,忽略其他影响因素,只考虑驱动力和加速度变化速率的比值,得到整车质量。
2 基于TruckSim软件的仿真
为了对比纵向动力学方法和运动学方法,基于TruckSim软件进行仿真分析。在TruckSim软件平台中基于某款试验车搭建试验汽车模型见图1,试验车部分参数见表1。
仿真实验中,考虑到路面坡度对质量识别的影响以及实车行驶状况,设计了表2的3种工况。工况1为水平路面,汽车加速升档行驶;工况2为从0°缓慢变化到6°的坡度路面,汽车低档加速行驶;工况3为加载1 t货物质量,汽车加速升档行驶。由于在仿真环境下可以得到理想的实验数据,故直接利用式(7)和式(11)进行质量辨识,实验结果如图2—4所示。
由表2可知,在3种工况下,动力学方法辨识车重比运动学方法好,收敛误差小。由于汽车换挡时,动力存在短暂中断以及离合器结合冲击,导致动力学辨识结果存在波动,但是换挡结束后,辨识效果较好。由图2可知,相比于动力学辨识方法,由于换挡后加速度变化剧烈,运动学方法辨识结果在实际质量上下波动显著,毛刺过多。当挡位固定、加速度缓慢平滑变化时,运动学辨识方法可以辨识汽车质量。由图3和图4可知,动力学辨识方法不受路面坡度影响,且能够有效辨识加载后的质量,而运动学方法在路面坡度变化工况下辨识效果较差。
结合汽车实际行驶状况,可以得出以下结论:1)动力学方法能够有效地辨识整车质量,对载货质量变化不敏感,换挡对辨识速度有较大影响;2)运动学方法受换挡、路面坡度、加速度变化影响较大。
3 质量辨识的试验验证
为验证TruckSim仿真结论的准确性以及进一步对比两种方法的辨识效果,采集了水泥路面工况下货车的行驶数据。试验车参数见表1。考虑到平原地区二级公路最大路面坡度为5%[17-18],可以认为平原地区路面坡度为0,故本文忽略路面坡度对质量辨识的影响。
如图5所示,从CAN总线上接收车速、发动机转矩、发动机转速信息,最后通过CANoe发送到上位机。
3.1 信号处理
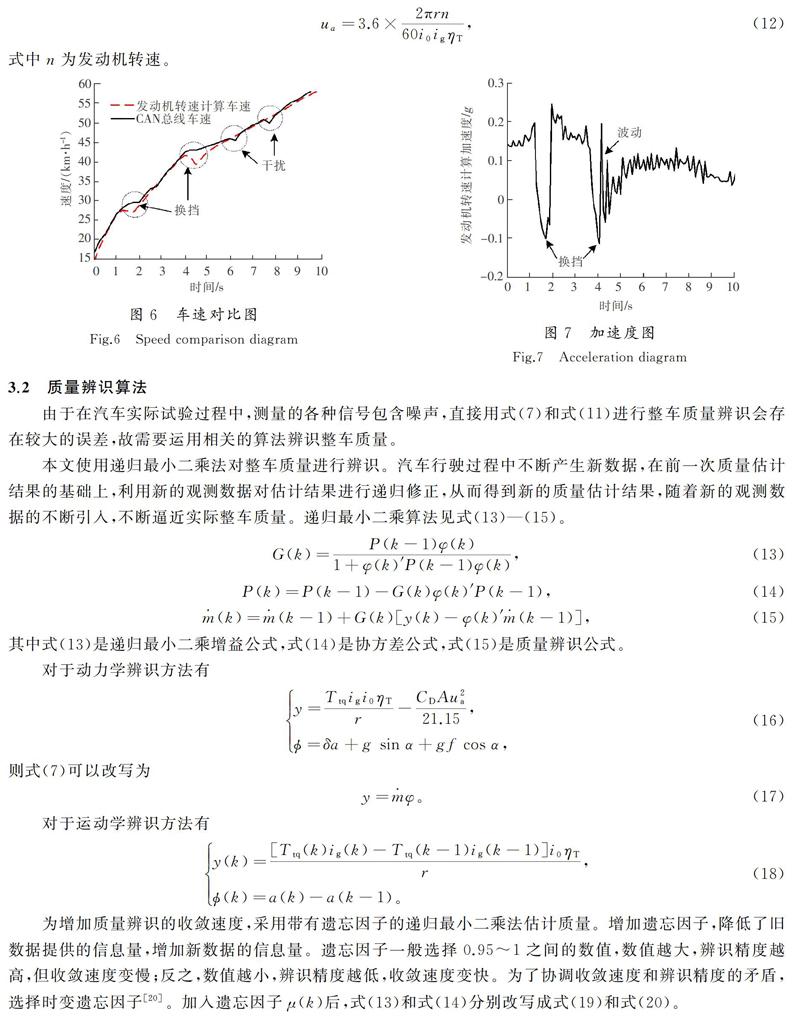
由于本试验的车速信号来源于ABS电控系统,车速传感器安装在车轮内侧,工作环境恶劣,且存在一定误差,车速信号求导后误差更大,故利用汽车动力传递关系(发动机输出动力经由离合器、变速器、主减速器传递到车轮)计算车速和加速度,车速计算公式见式(12),对车速求导后得到加速度。图6是CAN总线车速和发动机转速计算车速对比图。从图6可以看出,1.3 s和4 s时换挡,车速正常波动;而在6.4 s和7.8 s时,由于车速测量设备可能受到电磁、高温等外界干扰以及存在密封性不足等状况[19],出现了异常车速。而发动机转速计算车速相比于从CAN总线上读取车速,车速变化更加平稳,跳动小,精度高,更能准确地计算加速度。由于换挡期间,动力存在中断,使用一次滞后滤波对换挡期间的转速进行处理。图7是发动机转速计算加速度图,在4 s时,由于换挡不及时,导致离合器冲击度过大,造成较大的加速度波动。
3.2 质量辨识算法
由于在汽车实际试验过程中,测量的各种信号包含噪声,直接用式(7)和式(11)进行整车质量辨识会存在较大的误差,故需要运用相关的算法辨识整车质量。
本文使用递归最小二乘法对整车质量进行辨识。汽车行驶过程中不断产生新数据,在前一次质量估计结果的基础上,利用新的观测数据对估计结果进行递归修正,从而得到新的质量估计结果,随着新的观测数据的不断引入,不断逼近实际整车质量。递归最小二乘算法见式(13)—(15)。
为增加质量辨识的收敛速度,采用带有遗忘因子的递归最小二乘法估计质量。增加遗忘因子,降低了旧数据提供的信息量,增加新数据的信息量。遗忘因子一般选择0.95~1之间的数值,数值越大,辨识精度越高,但收敛速度变慢;反之,数值越小,辨识精度越低,收敛速度变快。为了协调收敛速度和辨识精度的矛盾,选择时变遗忘因子[20]。加入遗忘因子[WTBX]μ(k)后,式(13)和式(14)分别改写成式(19)和式(20)。
3.3 试验结果分析
使用上述数据处理方法得到的速度和加速度,用带遗忘因子的遞归最小二乘法进行质量辨识,绘制出图8—11。其中图8—10使用动力学方法,图11使用运动学方法。对比结果见表3。
对比图8和图9可知,经过换挡后,收敛时间变长,收敛过程波动变大,误差变化较小。对比图8和图10,整车质量变化时(1 000 kg),收敛时间和误差基本不变。而图11则表明,运动学方法辨识误差较大,收敛时间长。经分析,主要原因是速度信号本身具有一定误差,经过微分求导后,误差更大;此外受路面坡度和空气阻力影响明显以及操作过程中需要驾驶员缓慢轻踩油门踏板,故该方法在工程应用中局限性较高。
由表3知,笔者提出的动力学辨识质量算法可以在短期内有效地估计整车质量,在不换挡时收敛更迅速,且能够准确识别加载后的质量,鲁棒性好。在工程应用中,一旦检测到离合器处于分离状态,终止迭代计算,当检测到离合器处于结合状态,继续迭代计算,这样可以更准确及时地估计整车质量。而运动学辨识方法受外界干扰影响较大,且对驾驶员操作要求较高,实用性差,使用条件苛刻。
4 结 语
对货车的整车质量问题进行了研究,阐述了两种质量辨识方法,在TruckSim软件中建立模型并在多种工况下仿真,根据得到的数据直接计算整车质量,得到两种质量辨识算法的适用范围以及收敛影响因素。提出了速度和加速度的计算方法,并设计了整车质量估计算法,进行了实车试验验证,得出以下结论:
1)发动机转速计算车速的方法能够有效提高车速精度,并且能够准确地计算汽车加速度;
2)提出的整车质量估计算法能够有效地估计整车质量,换挡对算法的收敛速度有一定影响,但不影响辨识结果;
3)运动学货车整车质量辨识算法影响因素较多,鲁棒性差。
目前的研究是基于二级以上公路的试验工况,忽略了路面坡度对质量辨识方法的影响,且辨识方法只考虑纯纵向动力学。在后续的研究中将考虑路面坡度和横向运动的影响。
参考文献/References:
[1] 王洪亮, 张庆渴, 谷文豪, 等. 基于PID控制的坡道起步控制仿真与试验研究[J]. 汽车工程, 2017, 39(4): 480-485.
WANG Hongliang, ZHANG Qingke, GU Wenhao, et al. Simulation and experiment study on hill start control based on PID control[J]. Automotive Engineering, 2017, 39(4): 480-485.
[2] 王洪亮, 谷文豪, 张庆渴, 等. 汽车坡起中EPB的Bang-Bang控制研究[J]. 北京理工大学学报, 2017,37(1): 46-49.
WANG Hongliang, GU Wenhao, ZHANG Qingke, et al. Research on Bang-Bang control of EPB system in vehicle hill start[J]. Transactions of Beijing Institute of Technology, 2017,37(1):46-49.
[3] 王洪亮, 董巍, 李楠, 等. 中/重型汽车电子驻车系统设计及控制研究[J]. 河北科技大学学报, 2015, 36(2): 118-125.
WANG Hongliang, DONG Wei, LI Nan, et al. Design and research on the electronic parking brake system of the medium and heavy duty vehicles[J]. Journal of Hebei University of Science and Technology, 2015, 36(2): 118-125.
[4] 谷文豪, 王洪亮, 皮大伟, 等. 基于倾角传感器的坡道角度识别研究[J]. 河北科技大学学报, 2015, 36(6): 566-572.
GU Wenhao, WANG Hongliang, PI Dawei, et al. Research on recognition of ramp angle based on transducer[J]. Journal of Hebei University of Science and Technology, 2015, 36(6): 566-572.
[5] VAN ZANTEN A T. Bosch ESP system: 5 Years of experience[C]// Sae Congress. [S.l.]:[s.n.], 2000:211-220.
[6] MERSKY A C, SAMARAS C. Fuel economy testing of autonomous vehicles[J]. Transportation Research Part C, 2016, 65: 31-48.
[7] WINSTEAD V, KOLMANOVSKY I V. Estimation of road grade and vehicle mass via model predictive control[C]//IEEE Conference on Control Applications. [S.l.]:IEEE, 2005:1588-1593.
[8] ALTMANNSHOFER S, ENDISCH C. Robust vehicle mass and driving resistance estimation[C]//American Control Conference. [S.l.]:IEEE, 2016: 6869-6874.
[9] DAI Zhuo, WU Guangqiang. Estimation method of road slope and vehicle mass based on vehicle dynamics[J]. Automobile Technology, 2018(1):20-24.
[10]DREIER L C, SAUTER I G. System for Estimating a Vehicle Mass[P]. US: EP 2085656 A2, 2009.
[11]CHU W, LUO Y, JIAN L, et al. Vehicle mass and road slope estimates for electric vehicles[J]. Journal of Tsinghua University, 2014, 54(6): 724-728.
[12]冯源, 余卓平, 熊璐. 基于分段递推最小二乘估计的汽车质量辨识试验[J]. 同济大学学报(自然科学版), 2012, 40(11): 1691-1697.
FENG Yuan, YU Zhuoping, XIONG Lu. Experimental research on partitioned recursive least squares estimation of vehicle mass[J]. Journal of Tongji University(Natural Science), 2012; 40(11): 1691-1697.
[13]李远方. 重型车质量辨识及道路坡度状态估计方法研究[D]. 长春:吉林大学, 2012.
LI Yuanfang. Study on Quality Identification of Heavy Vehicles and Estimation of Road Slope Status[D]. Changchun: Jilin University, 2012.
[14]STEFANOPOULOU A. Recursive least squares with forgetting for online estimation of vehicle mass and road grade: Theory and experiments[J]. Vehicle System Dynamics, 2005, 43(1): 31-55.
[15]LI B, ZHANG J, DU H, et al. Two-layer structure based adaptive estimation for vehicle mass and road slope under longitudinal motion[J]. Measurement, 2017, 95: 439-455.
[16]OBERTOV D, BARDOV V, ANDRIEVSKY B. Vehicle speed estimation using roadside sensors[C]//International Congress on Ultra Modern Telecommunications and Control Systems and Workshops.[S.l.]: IEEE, 2015.
[17]中華人民共和国住房和城乡建设部. 中华人民共和国国家标准:城市道路工程设计规范[M]. 北京:中国建筑工业出版社, 2012.
[18]EDEN G. Vehicle Mass Emission Measurement[P]. US: US6387706, 2002-01-01.
[19]CATHEY F W, DAILEY D J. A novel technique to dynamically measure vehicle speed using uncalibrated roadway cameras[C]// IEEE Intelligent Vehicles Symposium.[S.l.]: IEEE, 2005: 777-782.
[20]PALEOLOGU C, BENESTY J, CIOCHINA S. A robust variable forgetting factor recursive least-squares algorithm for system identification[J]. IEEE Signal Processing Letters, 2008, 15: 597-600.
