R软件在统计学实验教学中的应用

黄新 王梦贤 周密

[摘 要] 在信息化和大数据背景下，统计学实验教学中引入一种合适的统计软件就变得十分重要。针对R软件的优势和统计学课程的特点，结合具体案例，探讨了R软件在统计实验教学实践中的应用，以此激发学生学习和使用R软件的兴趣，提高统计学的教学质量。

[关 键 词] R软件；统计学；实验教学

[中图分类号] G642 [文献标志码] A [文章编号] 2096-0603（2018）13-0068-02

统计学是高等学校许多专业的一门重要专业基础课，结合近年我们统计学实验教学经验，以自由免费的R软件为工具，使用案例式教学，让学生从案例中真正体验统计分析数据的整个过程，提高统计学的教学质量。

一、统计学课程

统计学是一门关于数据的搜集、分析、展示和解释的科学，其研究内容包括描述统计和推断统计两大类。描述统计主要是对现象进行调查，将得到的大量数据加以整理、简缩，制成统计图表，并就这些数据的分布特征计算出一些概括性的数字。推断统计是指利用样本资料推断总体特征的技术和方法，是在观察资料的基础上深入地分析、研究和推断，以推知资料本身以外的情况和数量关系，为进行决策提供数据依据。主要有参数估计和假设检验两种类型。

二、R软件的优势

R软件属于GNU系统的一个自由、免费、源代码开放的软件，由新西兰奥克兰大学的Robert Gentleman 和Ross Ihaka及志愿者共同开发的一种计算环境。R软件在网站上可以自由下载，安装简单。R软件拥有大量的统计程序包和统计计算函数，更新速度快，具有强大的数据处理能力和丰富的图形展示功能。许多统计方法和技术都可以在R软件中实现，如参数估计、假设检验、多元统计分析等。学生只需要根据实际问题，编写和调用相应的函数，便可灵活地进行数据统计分析，甚至创造出新的统计计算方法。

三、R软件的统计学实验教学案例分析

R软件是模拟实验与统计计算的有力工具，把R软件引入统计学教学中，将那些枯燥难懂的统计理论与有趣的统计实践工作联系起来，使统计理论教学变得妙趣横生，从而大大提高学生的学习积极性和教学效率。

（一）R软件在数据描述统计实验教学中的应用

数据描述统计是通过计算统计量与绘制统计图表等方法，可以更加直观、方便地表述数据的分布特征。

1.产生模拟100名学生统计学（Score1）、线性代数（Score2）两门课程的期末考试成绩。

>Xuehao=seq（1609001，1609100）# 生成100名学生的学号（1609001至1609100）

>set.seed（）#用于设定随机数种子

>Score1=round（rnorm（100，mean=70，sd=15））#生成均值为80，标准差为5的100个正态分布的随机整数 48 94 56 56 40 66 65 61 68 …… 55 83 72 86 65 77 60 66 55

>Score2=round（runif（100，min=40，max=100））#生成区间为[40，100]的100个均匀分布的随机整数 54 70 49 47 80 88 94 65 86 80 ……75 60 84 57 44 41 88 77 52

>X=data.frame（Xuehao，Score1，Score2）#将期末考试成绩汇总，生成数据框

>Zmean=colMeans（X）[c（“Score1”，“Score2”）]#求两门课程期末考试的平均成绩

>Zmean Score1 69.52 Score2 68.76

>Zscore=apply（X[c（“Score1”，“Score2”）]，1，sum）#求每位学生三门课程成绩的总分

>Zscore 92 183 153 112 90 108 116 139 1 ……134 161 135 163 122 125 116。

2.数据描述统计中的几种常用图形

（1）直方图 >par（mfrow=c（1，2））如图1。

>Tjx=hist（X$Score1，main=“统计学期末考试成绩”，col=“12”，xlab=“分数”）

>Xxds=hist（X$Score2，main=“线性代数期末考试成绩”，col=“12”，xlab=“分数”）

统计学期末考试成绩 线性代数期末考试成绩

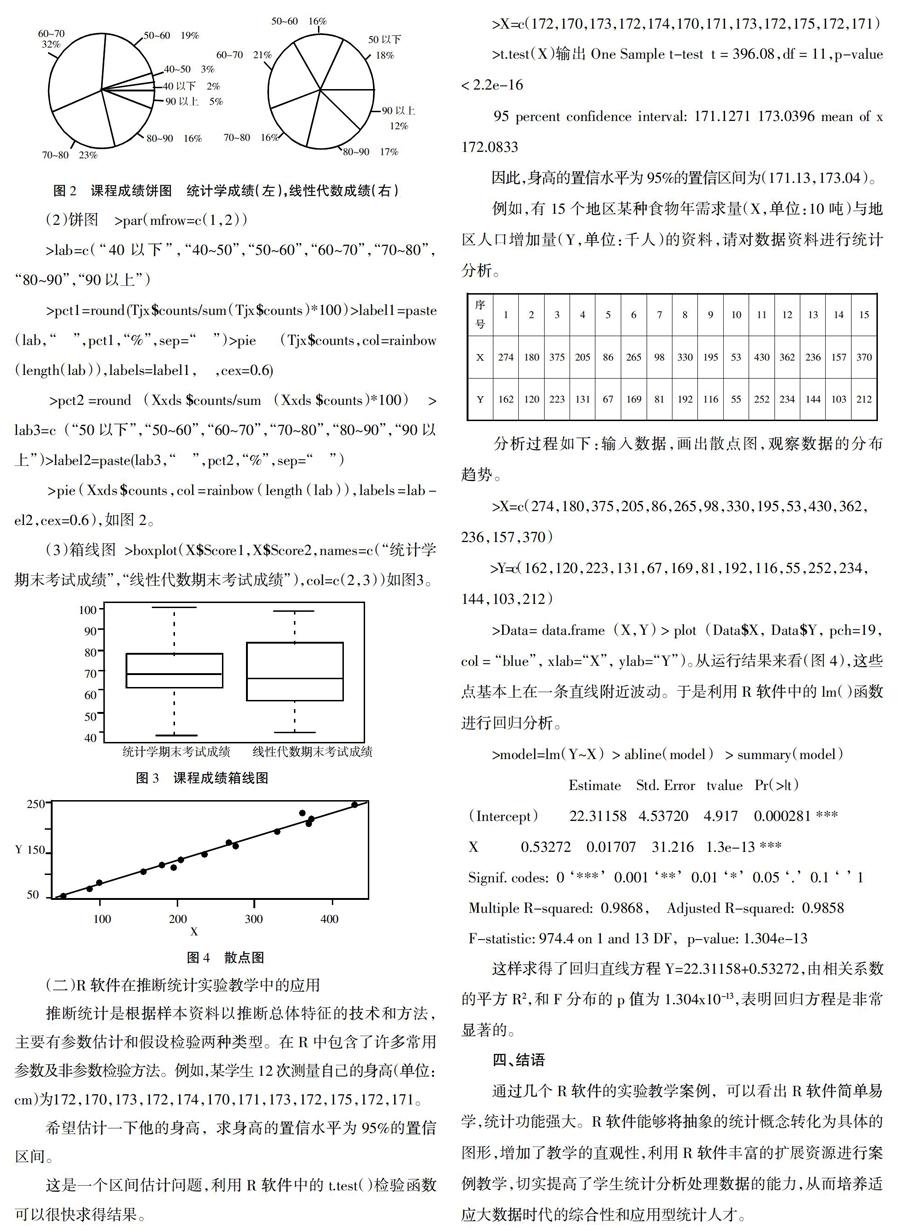
（2）饼图 >par（mfrow=c（1，2））

>lab=c（“40以下”，“40～50”，“50～60”，“60～70”，“70～80”，“80～90”，“90以上”）

>pct1=round（Tjx$counts/sum（Tjx$counts）*100）>label1=paste（lab，“ ”，pct1，“%”，sep=“ ”）>pie （Tjx$counts，col=rainbow（length（lab）），labels=label1， ，cex=0.6）

>pct2=round（Xxds$counts/sum（Xxds$counts）*100） > lab3=c（“50以下”，“50～60”，“60～70”，“70～80”，“80～90”，“90以上”）>label2=paste（lab3，“ ”，pct2，“%”，sep=“ ”）

>pie（Xxds$counts，col=rainbow（length（lab）），labels=lab-el2，cex=0.6），如圖2。

（3）箱线图 >boxplot（X$Score1，X$Score2，names=c（“统计学期末考试成绩”，“线性代数期末考试成绩”），col=c（2，3））如图3。

（二）R软件在推断统计实验教学中的应用

推断统计是根据样本资料以推断总体特征的技术和方法，主要有参数估计和假设检验两种类型。在R中包含了许多常用参数及非参数检验方法。例如，某学生12次测量自己的身高（单位：cm）为172，170，173，172，174，170，171，173，172，175，172，171。

希望估计一下他的身高，求身高的置信水平为95%的置信区间。

这是一个区间估计问题，利用R软件中的t.test（）检验函数可以很快求得结果。

>X=c（172，170，173，172，174，170，171，173，172，175，172，171）

>t.test（X）输出One Sample t-test t = 396.08，df = 11，p-value < 2.2e-16

95 percent confidence interval： 171.1271 173.0396 mean of x 172.0833

因此，身高的置信水平为95%的置信区间为（171.13，173.04）。

例如，有15个地区某种食物年需求量（X，单位：10吨）与地区人口增加量（Y，单位：千人）的资料，请对数据资料进行统计分析。

分析过程如下：输入数据，画出散点图，观察数据的分布趋势。

>X=c（274，180，375，205，86，265，98，330，195，53，430，362，

236，157，370）

>Y=c（162，120，223，131，67，169，81，192，116，55，252，234，

144，103，212）

>Data= data.frame（X，Y） > plot（Data$X， Data$Y， pch=19， col = “blue”， xlab=“X”， ylab=“Y”）。從运行结果来看（图4），这些点基本上在一条直线附近波动。于是利用R软件中的lm（）函数进行回归分析。

>model=lm（Y～X） > abline（model） > summary（model）

Estimate Std. Error tvalue Pr（>|t）

（Intercept） 22.31158 4.53720 4.917 0.000281 ***

X 0.53272 0.01707 31.216 1.3e-13 ***

Signif. codes： 0 ‘*** 0.001 ‘** 0.01 ‘* 0.05 ‘. 0.1 ‘ 1

Multiple R-squared： 0.9868， Adjusted R-squared： 0.9858

F-statistic： 974.4 on 1 and 13 DF， p-value： 1.304e-13

这样求得了回归直线方程Y=22.31158+0.53272，由相关系数的平方R2，和F分布的p值为1.304x10-13，表明回归方程是非常显著的。

四、结语

通过几个R软件的实验教学案例，可以看出R软件简单易学，统计功能强大。R软件能够将抽象的统计概念转化为具体的图形，增加了教学的直观性，利用R软件丰富的扩展资源进行案例教学，切实提高了学生统计分析处理数据的能力，从而培养适应大数据时代的综合性和应用型统计人才。