Modeling of thermodynamics of ice and water in seasonal ice-covered reservoir *
2018-05-14NanLi李楠YoucaiTuo脱友才YunDeng邓云RuidongAn安瑞冬JiaLi李嘉
Nan Li (李楠), You-cai Tuo (脱友才), Yun Deng (邓云), Rui-dong An (安瑞冬), Jia Li (李嘉),
Rui-feng Liang (梁瑞峰)
State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065,
China
Introduction
The reservoir ice is a common hydrologic phenomenon in the winter in cold regions, and it is an important issue in the design and the operation of Hydro power stations[1]. The presence of the ice cover in reservoirs prevents the exchange of mass, energy and momentum between the atmosphere and the water surface, to form a biological environment under the ice as a closed system[2]. The thermal stratification,especially in large reservoirs, also occurs in winter.Additionally, the Hydro power operations will alter the flow, thermal and ice regimes in downstream[1]. As Hydro power projects are continually developed in cold regions of China in recent years, better understanding of the thermal-ice dynamic process of reservoirs is essential to manage Hydro power operations and water resources in winter[1,3,4].
The ice processes in reservoirs and rivers are complex, with supercooling water, formation of ice,ice transport, and thermal growth and decay of ice cover, which are mainly affected by air temperature,wind, flow conditions, and topographic features[5].The field observation is the most direct and common approach to establish the relationship between the ice processes and these influential factors. Russian researchers investigated more than 30 reservoirs from the 1950s to the 1980s, with many important findings on the variations of reservoir ice conditions, such as the sequence of freeze-up and break-up and the distribution of the ice thickness, as described in a review literature[1]. With the large heat capacity in deep reservoirs, the longitudinal temperature difference in a reservoir can reach 7°C before the freeze-up period,with a large difference of the ice conditions in the reservoir[6]. Due to its complexity, the thermal-ice processes in large reservoirs are still not well understood.
Mikova andKalinin[7]proposed relationships between the reservoir ice cover thickness and the cumulative freezing-degree-days. Coupled mathematical models of the vertical 1-D water temperature and the ice cover were developed to study the thermal and ice regime in reservoirs or lakes[8,9], but the spatial variation of the ice regime is not considered in these models. The ice cover thickness in the reservoir is not uniform, since the thermal structure of the reservoir varies with the variations of the water depth and the inflow, and the formation of the initial ice cover is determined by a heat balance. Oveisy et al.[10]implemented an ice-formation algorithm into the 3-D lake model (ELCOM) to simulate the ice thickness and the thermal regime. They assume that the ice cover will form when the water surface temperature reaches the freezing point.
In this study, a thermal-ice model is coupled into a laterally averaged 2-D water temperature model, as verified by the field data in the Ertan Reservoir[11].The heat and hydrodynamics conditions are considered in the model for the formation of the initial ice cover. With the model, the growth and the decay of the ice cover in the reservoir can be simulated, as well as the temporal variation of the water temperature distribution in the reservoir. This model is applied to the Fengman Reservoir located in Jilin, China. The simulated results of the water temperature and the ice thickness are in a good agreement with the observed data.
1. Mathematical model
The water temperature in large reservoirs has longitudinal and vertical variations, which may affect the development of the ice cover. With the differences of the ice condition caused by the transverse water temperature distribution ignored, a numerical model combining the 1-D thermodynamic feature of the ice cover and the laterally-averaged 2-D water temperature distribution is developed in this study to simulate the ice regime and the water temperature in reservoirs.
1.1 Ice cover thickness
The ice cover in a reservoir can be regarded as a floating ice slab on the surface of the reservoir, and the growth and the decay of the ice cover take place at the ice-water and air-ice interfaces. Therefore, the variation of the ice cover thickness is caused by the heat exchanges across these two interfaces.
Neglecting the influence of the snow cover, the 1-D heat conduction equation in the ice cover is described as[12]
whereiρ is the density of the ice,iTis the temperature in the ice cover,Ciis the specific heat of the ice,kiis the heat conduction coefficient of the ice, andφz(z,t) is the rate of the internal heat source due to the adsorption of the shortwave penetration.
Whenthe value of φiais negative, the phase change does not take place across the ice surface, and the ice cover will lose heat through the ice surface,which can be expressed as

When the value ofiaφ is positive, the ice surface will melt, which can be expressed as

At the bottom of the ice cover, the heat balance at the ice -water interface can be expressed as

where φiais the heat flux at the ice-water interface,qwiis the heat flux from the water to the ice,Liis the latent heat of the ice, andHis the thickness of the ice cover.
Equations (2)-(4) define the boundary conditions of Eq. (1), which is a nonlinear equation. In this study,the linear distribution of the temperature in the ice cover is assumed. The validity of this assumption for a thin ice cover was examined by Greene[13]. The time dependent ice growth and decay in the reservoir is approximated by a one-dimensional, quasi-steady state calculation at each time step. Equation (1) can be expressed as[13]

whereTfis the freezing point of the water, andTisis the temperature of the surface ice. Equation (5) is used herein to simplify the calculation of the ice cover in the reservoir. When solving for the temperature of the surface ice, ifTisis above the freezing point,Tisis set to the freezing point, theniaφ will be recalculated for determining the melting thickness at the top of the ice cover.
The current understanding of the reservoir ice formation remains to be improved. The initial ice cover in the reservoir is assumed to come from the formation of skim or border ice. Huang et al.[14]proposed empirical criteria for the formation of border ice and skim ice in the river when the surface water temperature is supercooled and the turbulence is small under the flow and wind conditions. These criteria are used here to simulate the initial ice formation in the open water portion of the area. Once the initial ice cover (hi0) is formed, the variation of the ice cover thickness will be governed by the thermal effects across the ice-water and ice-air interfaces. The following criteria by Matousekʼs formulation can be used for a static ice cover formation: (1) The surface temperature of the waterTwsis less than a critical valueTcr, (2) The local surface velocity is less than 0.07 m/s.
The surface temperature of the waterTwsis evaluated by using an empirical relationship

whereTwis the average temperature in the surface layer of the water,Tcris a critical water temperature,φwais the rate of heat loss from the water to the atmosphere,usis the local flow velocity in the surface layer,Wis the wind velocity, andbis a coefficient related to the surface width in the wind direction.
1.2 Hydrodynamic governing equations
The hydrodynamic governing equations include the continuity equation, the momentum equations, and the energy equations. The Boussinesq approximation is used in this study, which means that the buoyant effect is considered only in the gravity term. Therefore,the hydrodynamic and water temperature equations in the 2-D Cartesian coordinate system are:


whereGkis the production of the kinetic energy from the mean flow,Gbis the production or the loss of the turbulent kinetic energy by the buoyant forces,νe=ν+νt, ν is the molecular viscosity and νtis the kinematic eddy viscosity, νt=Cμk2/ε,u,ware the longitudinal and vertical velocity components,respectively,pis the intensity of pressure,Bis the river width,kis the turbulent kinetic energy, ε is the dissipation rate of the turbulent kinetic energy,sρ is the reference density of water,Tis the water temperature,zφ is the solar radiation flux through the water depth,kσ,εσ,Tσare the Prandtl number of the turbulent kinetic energy, the dissipation rate and the temperature, respectively, and constantsCw,Cε1,Cε2are 0.09, 1.44, 1.92, respectively.
Neglecting the effect of the pressure variation with the density, the relationship between the density and the temperature can be approximately described as


1.3 Heat exchange processes
The heat exchange across the air-water interface in the open water includes four components: the shortwave radiation, the long wave radiation, the evaporation heat flux, and the sensible heat flux. The budget can be estimated by using an empirical formula[11].The air-water heat exchange is briefly described as
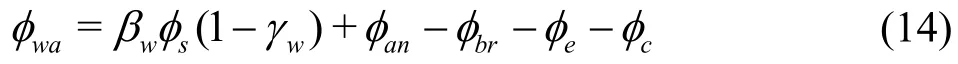
wheresφ is the incoming solar radiation,wβ is a fraction of the absorbed solar radiation that penetrates through the water surface (the first 1.0 m depth of the water), γwis the albedo of the solar radiation at the water surface, φanis the atmospheric long wave radiation,brφ is the long wave radiation emitted from the water surface,eφ is the heat flux from the reservoir water surface due to the evapo-condensation,andcφ is the heat flux conducted from the water surface as the sensible heat by the air.eφ andcφ are related to the water surface temperatureTws.
The ice-air heat exchange is similar to the water air interface exchange. When the reservoir is ice covered, the coefficientsCeandCcare introduced into the calculation of the evapo-condensation and the conductive heat transfer,with the ice surface temperatureTisbeing used in the place of the water surface temperatureTw. The budget for the ice-air heat ex- change is described as

whereiγ is the albedo of the solar radiation at the ice surface, φibris the long wave radiation emitted from the ice surface, andiηis the bulk extinction coefficient in the ice.
The shortwave radiation that penetrates into the water attenuates exponentially along the depth directionz, and it is related with the water transparency

With the presence of the ice cover, the shortwave radiation that penetrates into the water underneath the ice cover is

wheredis the water depth,wηandiηare the bulk extinction coefficients of the water and the ice,respectively.
The heat flux from the water to the ice has significant effects on the thickness of the ice cover and the water temperature beneath the ice cover. It is determined by a bulk formula obtained based on the experimental data[15]

whereChis the ice-water heat transfer coefficient.
1.4 Hydraulic boundary conditions
The symmetry conditions for velocities are given on the free surface of the reservoir. The reservoir bottom and the dam face are taken as no-slip boundaries, and they are regarded as adiabatic. The velocityuis calculated based on the flow at the inflow boundary andwis zero at the inflow and outflow boundaries. The inflow temperature is given in a day, and a zero gradient condition is set at the outflow boundary in every time step. The values ofkand ε at the inflow boundary can be given as:

whereuiis the velocity of the inlet,ihis the depth of the inlet.
1.5 Numerical approach
A finite volume method is employed to solve the governing equations (7)-(12). The staggered grid method is used to reduce the numeric diffusion, and the modified SIMPLE algorithm is applied to solve the pressure term. The calculations of the ice and flow fields are separated, and the grid of the ice calculation is the same as that of the surface water temperature.The temperature of the ice surface (Tis) is computed through an iterative method based on Eq. (2) and Eq.(5), becauseiaφ is a nonlinear function ofTis.
In the iterative procedure, all governing equations are solved in a given time step, until the resultssatisfy the convergence condition. To improve the computational efficiency, a parallel computing method for the flow and temperature fields is used in this study[16].

Table 1 Model parameter values used in simulation
2. Model validation and result analysis
The thermal-ice model described in the preceding sections is applied to a 153 km reach of the Fengman Reservoir. The Fengman Reservoir is a typical large reservoir with seasonal ice cover. Detailed field data of the water temperature and the ice conditions of the reservoir during the period of 2010-2011 are used to test the capacity of this model[17].
In the numerical simulation, the reservoir is discretized into 523 (longitudinal)×72 (vertical) rectangle elements. The observed temperature data on June 25, 2010 is taken as the initial condition of the temperature field. The simulation is carried out for 321 d with a time step of 30 s. Values of model parameters are summarized in Table 1.

Fig.1 Comparisons of simulated and observed water temperatures in Fengman Reservoir (the contour represents the computed data, the solid rectangular represents the measured data, and the figures in the plot are the water temperatures in degrees)
The comparisons of the water temperature and the ice thickness between the simulated results and the observed data are shown in Figs. 1-4,Eis the elevation,Lis the distance from the tail of the reservoir.The simulated thermal stratification and the outflow temperature in the Fengman Reservoir with consideration of the effects of the topography, the meteorology,and the reservoir operation are in a good agreement with the field data. In the ice season, the ice cover provides a thermal protection for the water due to the less heat flux through the ice-water interface. The water temperature in front of the dam sees an inverse distribution, with a high outflow temperature about 2°C-3°C from the deep water intake during the icecovered period. The error of the vertical temperature profile especially in March may come from the flow disturbance due to the intake. Compared with the temperature before the construction of the Fengman Reservoir, the outflow temperature decreases by 5.8°C in average from April to August (the maximum value is 11.9°C in July), and the outflow temperature rises 5.1°C in average from September to the next March(the maximum value is 10.7°C in December). These comparison results indicate that the Fengman Reservoir has a thermal storage capacity. The ice cover in front of the dam stays intact for 106 d, and the simulated time of the freeze-up and the break-up are 2 d and 1 d later than the observed values,respectively. The simulated thickness variation agrees well with the observed data (Fig.4).

Fig.2 Comparisons of simulated and observed vertical water temperature profiles in front of Fengman dam

Fig.3 Comparison of simulated and observed outflow temperatures
In autumn, due to the effect of the inflow and the heat storage capacity in different parts of the Fengman Reservoir, one sees an increase of the surface water temperature from the tail to the dam. This phenomenon was observed in October, 2012[6], and is well simulated by our model. Affected by the large water replacement rate, the surface water temperature in the middle of the Fengman Reservoir (40 km-80 km from the tail of the reservoir) is dropped to 4°C and the temperature is reached earlier than in the place close to the dam. When the surface layer water temperature drops below 4°C, the vertical water temperature structure will be reversed due to the fact that there is no mixing in the whole depth. When the surface temperature satisfies the condition of freezing, a static ice cover forms. In the Fengman Reservoir, the formation of the ice cover starts from the middle reach,then it is extended towards the dam and the tail. When the reservoir is ice covered, a surface buoyant flow is observed underneath the front of the ice cover (as shown in Fig.5). A 4°C vertical isotherm surface clearly divides the reservoir into two parts: the open water part with temperature above 4°C, and the ice-covered or icing part with temperature below 4°C.The moving speed of this isotherm surface is in agreement with that of the ice cover front edge towards the dam, because the water surface temperature below 4°C would soon drop to the freezing point to form the ice cover.

Fig.4 Comparison of simulated and observed ice thicknesses in front of Fengman dam
The cooling rate in the reservoir before the freeze-up period in typical sections of the Fengman Reservoir is shown in Table 2. The air temperature and the water depth are two major factors to determine the cooling rate. The cooling rate near the dam is smaller than that in the tail, because the deep water in front of the dam has a larger heat storage capacity. To clarify the contribution of the air temperature and flow to the water cooling in different parts, a differential element method is set up, which is applied to the vertical homoeothermic water in the cooling. According to the theory of the heat balance, the energy equation is

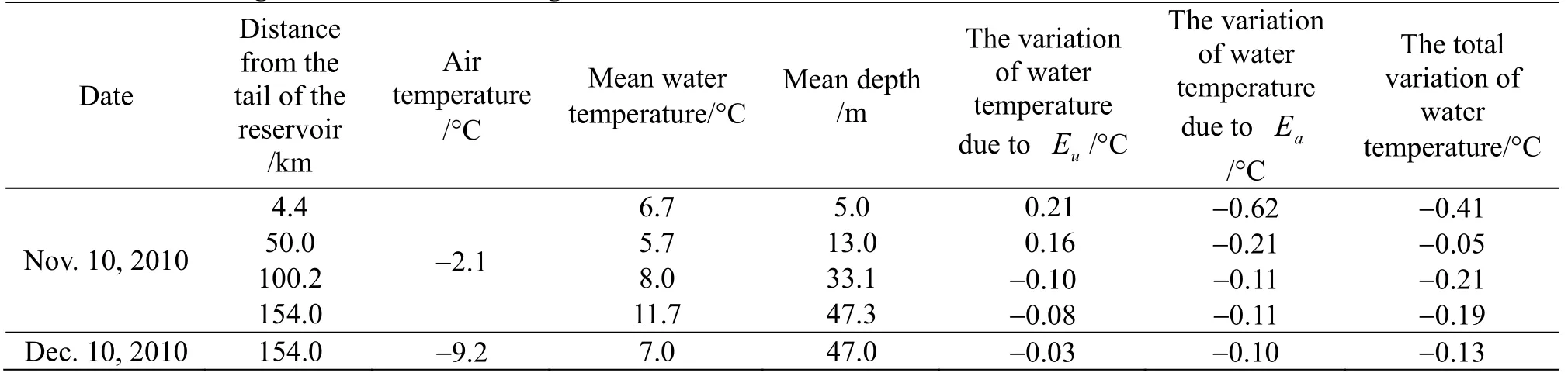
Table 2 The cooling rate in sections of Fengman Reservoir
whereEais the part of the air that has the effect on the energy of the differential element volumeV,Euis the part of the flow that has the effect on the energy of the differential element volume,EVis the energy change part of the differential element volume in time Δt, Δsis the surface area of the differential element,are the depth-average water temperatures and the velocities at the inflow and the outflow, respectively, andAin,Aoutare the cross-sectional areas of the inflow and the outflow,respectively.
The water in the reservoir has different cooling rates on November 10, 2010. The high and stable inflow temperature has a positive contribution to the heat of the section in the tail of the reservoir. The total cooling rate in the reservoir decreases with the depth,but the rates of the flow and the air are both roughly a same function of the drop of the water volume in deeper sections (>50 km from the tail of the reservoir). The cooling rate in front of the dam on December 10, 2010, indicates that the effect of the flow on the cooling in the reservoir decreases when the air temperature drops.
The freeze-up period in the reservoir lasts 30 d,starting on November 30 in the middle reach, and ending on December 29 in front of the dam. The sequence of the freeze-up is from the mid reach of the reservoir to the dam. Figure 6 shows the variations of the ice thicknesses in the reservoir during winter. The maximum ice thickness is in the earliest frozen parts and remains so until the break-up period. The maximum ice thickness in the middle reaches 1.0 m,while the maximum thickness in front of the dam is about 0.7 m. During the break-up period, the sequence of the break-up is from the tail to the dam due to the high inflow and air temperature. Figure 1(b) shows that the surface water temperature decreases in the reservoir, which means that one may see a buoyant flow after the break-up in the reservoir. A 10 km open channel is observed in the tail of the reservoir and its temperature keeps about 2.0°C in the whole ice season,with a high inflow water temperature from the Baishan power station.
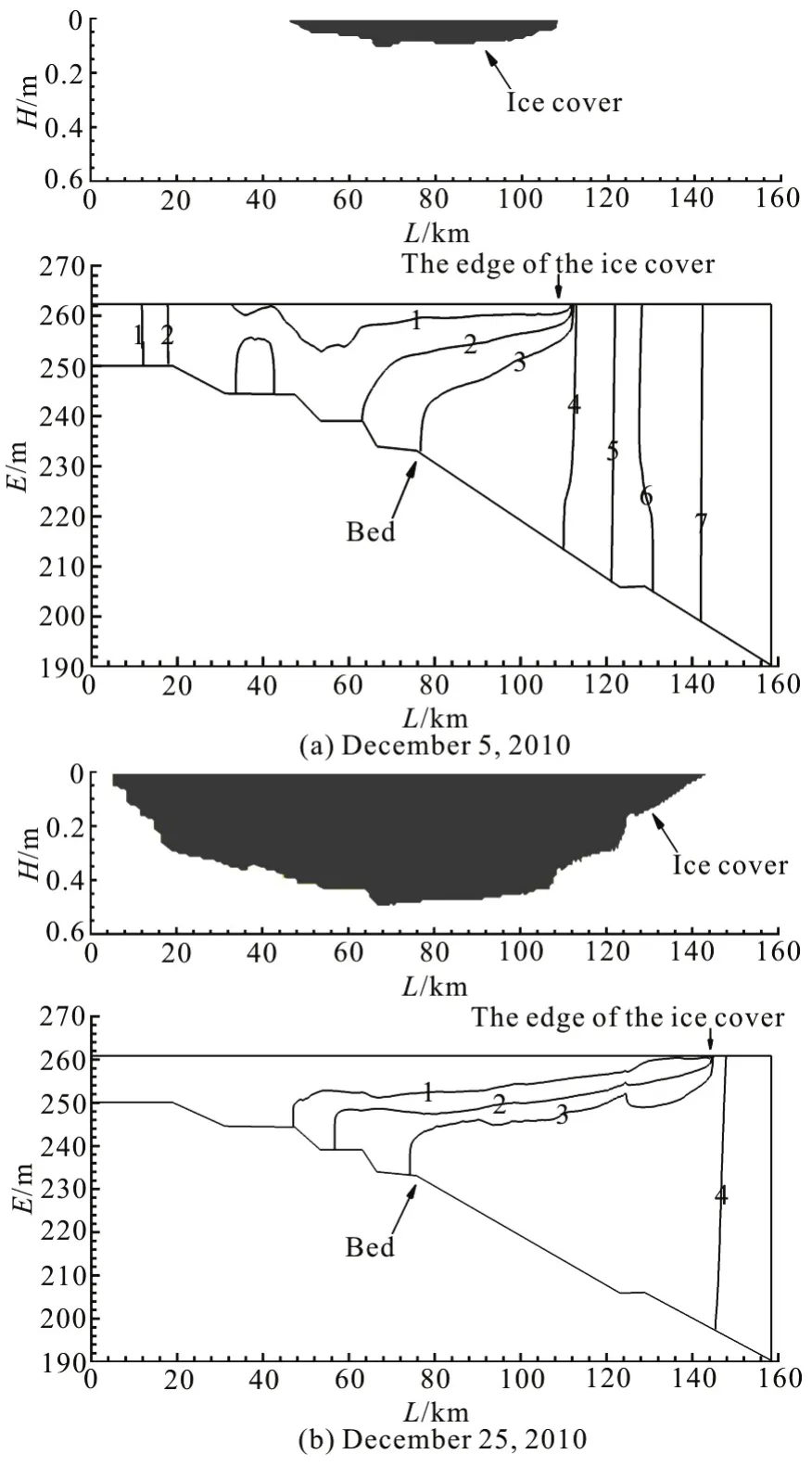
Fig.5 Simulated water temperature distributions on December 5 and December 25, 2010
3. Discussions
The ice processes, including the supercooling of the water, the formation of frazils and border ices, and the transport of ice floes, are mainly affected by the hydrodynamics and the wind, which makes the formation of the initial ice cover in the reservoir very complicated. Actually, the initial ice thickness can reach 0.2 m, due to the ice transport by the flow and the wind waves. Donchenko[1]proposed an empirical formula to quantify the intensity of the ice formation based on the field observations, but it is difficult to use this formula for modeling the freeze-up ice processes. Huang et al.[14]applied a river ice model[5]to simulate the freeze up process in the upper St.Lawrence River without consideration of the water temperature variation over the depth. The model of the ice cover evolution should be implemented in reservoir models in the future.

Fig.6 Variations of simulated ice thicknesses in the reservoir during the ice period
The deterioration of the ice cover during the melting periods is a thermal process, which includes the heat exchange through the ice-water and ice-air interfaces. The solar radiation that penetrates the ice cover has an important effect on the melting of the internal ice, which reduces the density and the intensity of the ice cover[18]. The wind stress and the rainfall are also important factors to accelerate the melting of the top of the ice surface[1]. Most of the previous studies are based on the field observations,and the present ice models do not include the formulation of the ice dynamics during the melting period. With the ice dynamic process ignored, the water temperature distribution in the Fengman Reservoir can be well simulated, and the maximum difference between the simulated and observed water temperatures reaches 0.8°C in front of the dam. It indicates that the ice regime and the accurate water temperature in the reservoir are necessary in a comprehensive formulation of the model.
4. Conclusions
In the present study, a numerical model is developed for simulating the thermodynamics of the water and the ice in a reservoir. The flow and the temperature distribution are simulated by the laterally averaged 2-Dk-εturbulent equations. The growth and the decay of the ice cover are simulated by using the Stefan’s equation, and a linear temperature distribution over the thickness of the ice cover is assumed. The heat exchanges through the air-ice and ice-water interfaces are included in the formulation.With consideration of the effect of the local heat and hydrodynamics conditions, an empirical formula is proposed to improve the evaluation of the formation of the initial ice cover
The model is applied to the Fengman Reservoir for a period from 2010 to 2011. The comparison between the simulated results and the field data shows that the model can be used to simulate the ice conditions including the ice thickness, the freeze-up and the break-up, as well as the water temperature distribution. Due to the variation of the heat conditions and the freeze-up time in the reservoir, the thickness of the ice cover is not uniform in the reservoir. The surface buoyant flow that occurs at the freeze-up and break-up periods affects the growth and the decay of the ice cover and the heat distribution in the reservoir.
[1] Cai L. River ice conditions in China [M]. Zhengzhou,China: Yellow River Water Conservancy Press, 2008(in Chinese).
[2] Clilverd H., White D., Lilly M. Chemical and physical controls on the oxygen regime of ice-covered Arctic lakes and reservoirs [J].Journal of the American Water Resources Association, 2009, 45(2): 500-511.
[3] Fu H., Guo X. L., Yang K. L. et al. Ice accumulation and thickness distribution before inverted siphon [J].Journal of Hydrodynamics,2017, 29(1): 61-67.
[4] Zhao X., Lian J. J., Song X. Y. Analyses of the stability of submerged ice blocks [J].Journal of Hydrodynamics,2017, 29(3): 460-469.
[5] Shen H. T. Mathematical modeling of river ice processes[J].Cold Regions Science and Technology, 2010, 62(1):3-13.
[6] Tuo Y., Deng Y., Li J. et al. Water temperature and ice conditions in Fengman Reservoir, winter of 2012-2013[C].22nd IAHR International Symposium on Ice,Singapore, 2014, 434-441.
[7] Mikova K. D., Kalinin V. G. Methodology of evaluation of forecasts of the reservoir ice cover thickness (the Votkinsk reservoir case study) [J].Russian Meteorology and Hydrology,2008, 33(10): 676-679.
[8] Tuo Y. C., Deng Y. and Huang F. B. et al. Study on the coupled mathematical model of the vertical 1D temperature and ice cover in the reservoir [J].Journal of Sichuan University (Engineering Science Edition), 2011,43(5): 39-44(in Chinese).
[9] Gebre S., Boiss Y., Alfredsen K. Sensitivity to climate change of the thermal structure and ice cover regime of three Hydro power reservoirs [J].Journal of Hydrology,2014, 510(6): 208-227.
[10] Oveisy A., Boegman L., Imberger J. Three-dimensional simulation of lake and ice dynamics during winter [J].Limnology and Oceanography,2012, 57(1): 43-57.
[11] Deng Y., Zhao W., LI J. et al. Simulation on thermal stratification of the huge-cubage and deep reservoirs [C].Proceedings of the 29th IAHR Congress,Beijing, China,2001, 584-593.
[12] Tuo Y., Deng Y., Li J. et al. Effects of dam reconstruction on thermal-ice regime of Fengman Reservoir [J].Cold Regions Science and Technology, 2018, 146: 223-235.
[13] Greene G. M. Simulation of ice-cover growth and decay in one dimension on the upper St. Lawrence River [R]. Ann Arbor, USA: Great Lakes Environmental Research Laboratory, 1981.
[14] Huang F., Shen H. T., Knack I. Modeling border ice formation and cover progression in rivers [C].21st IAHR International Symposium on Ice, Dalian, China, 2012,139-149.
[15] Li N., Tuo Y. C., Deng Y. et al. Heat transfer at ice-water interface under conditions of low flow velocities [J].Journal of Hydrodynamics,2016, 28(4): 603-609.
[16] Liang R. F., Li J., Li K. F. et al. A parallelism study on laterally averaged 2D reservoir water temperature model[J].Journal of Sichuan University (Engineering Science Edition), 2009, 41(1): 30-33(in Chinese).
[17] Tuo Y. C., Liu Z. G., Deng Y. et al. Water temperature of the Fengman Reservoir with seasonal ice cover [J].Advances in Water Science, 2014, 25(5): 731-738(in Chinese).
[18] Leppärant A. M., Terzhevik A., Shirasawa K. Solar radiation and ice melting in Lake Vendyurskoe, Russian Karelia [J].Hydrology Research,2010, 41(1): 50-62.
猜你喜欢
杂志排行
水动力学研究与进展 B辑的其它文章
- Some notes on numerical simulation and error analyses of the attached turbulent cavitating flow by LES *
- Energy dissipation of slot-type flip buckets *
- Transient aerodynamic characteristics of vans during the accelerated overtaking process *
- Numerical analyses of ventilated cavitation over a 2-D NACA0015 hydrofoil using two turbulence modeling methods *
- Revisit submergence of ice blocks in front of ice cover-an experimental study *
- 2-D eddy resolving simulations of flow past a circular array of cylindrical plant stems *
