Some notes on numerical simulation and error analyses of the attached turbulent cavitating flow by LES ＊

Xin-ping Long (龙新平), Yun Long (龙云), Wen-ting Wang (王文婷), Huai-yu Cheng (程怀玉),Bin Ji (季斌)

1. State Key Laboratory of Water Resources and Hydro power Engineering Science, School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China

2. Key Laboratory of Jet Theory and New Technology of Hubei Province, Wuhan University, Wuhan 430072,China

It is a great challenge for both experiment and numerical simulation to investigate the complicated transient cavitating flow. It is noted that numerical simulation of cavitating flow has achieved a remarkable progress in the last two decades. Li et al.[1,2]propose an improved all-speed Roe scheme for LES and obtain satisfactory results. The re-entrant jet[3]and shock wave[4]has attracted much attention. Peng et al.[5]observe the U-type fl ow structures around the hydrofoils in the cavitation tunnel. Ji et al.[6], Wang et al.[7], Long et al.[8]and Cheng et al.[9]study transient cavitating flow structure by high performance numerical methods and three-dimensional Lagrangian technology.

All these researches enhance the understanding of the transient cavitating flow. However, less attention are paid to assessing the accuracy of these numerical results with systematic methodology and procedures. Verification and validation (V&V) is a basic procedure to evaluate the accuracy and reliability of numerical simulation, but the practical use of LES V&V is a big challenge[10]. Related studies of LES V&V are ongoing[11]. Freitag and Klein[12]have proposed a systematic grid and model variation method to estimate the numerical and modeling error.Xing[11]proposes a general framework for V&V of LES to get the numerical, modeling and their coupling errors. The investigations by Dutta and Xing[13]have achieved promising achievements.

Inspired by the aforementioned studies, this letter carries out the large eddy simulation and error analysis of the attached turbulent cavitating flow around the Clark-Y hydrofoil. Comparisons between available experiments[14]and numerical results have been made. Quantitative analyses of LES errors are presented and cavitation influence on LES errors is also discussed.

The chord lengthCof hydrofoil is 0.07 m and angle of attack is 8°. The length, width and height of the computational domain are 10.0C, 0.3Cand 2.7C, respectively. The boundary inlet velocity is set asU∞=10m/s , and outlet boundary is fixed at the static pressure pout, deriving from the cavitation number σ=0.8 (σ=(pout-pv)/(0.5ρU∞2)), wherepvis the saturated vapor pressure andρis the liquid density). Detailed information about the setup can see Ref. [15]. Case 1 is refined with the same mesh topology from Case 3, and Case 2 is the same as Case 1 except for the change of Smagorinsky constant.Detail information about mesh, model constant and calculations setup has been displayed in Table 1.

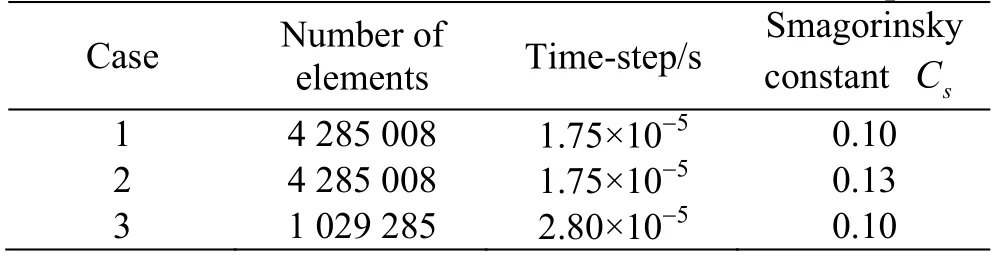
Table 1 Mesh and model constant and calculation setup

Herein, the LES errors estimation method, proposed by Freitag and Klein[12], has been employed.Some revised thoughts by Xing[11]have been adopted in this paper considering that the time step and grid spacing changing simultaneously. The numerical error and modeling error are estimated with power series expansions as a function ofh*and Δ:

whereSCis the numerical benchmark,S1,S2,S3denotes the standards LES solution, the LES solution with a modified model contribution and solution on a coarser mesh, respectively.cNandcMare the unknown coefficient. The local spatial and temporal resolutionh*[11]is defined as

where Δtis the time step andhis the local mesh size. Herehis equal to the filter width Δ. The model variation factor α=1.3. The time step and grid spacing share the same refinement ratior=1.6.pNandpMhas a large effect on the LES errors estimations.pN=1.7 andpM=1.5 were recommended by Dutta and Xing[16], whilepN=2 andpM=2/3 by Freitag and Klein[12]have been investigated and applied in some researches. Therefore,pN=2 andpM=2/3 are adopted in this paper.

The numerical error and modeling error for case1 are corresponding to the first term and second term on the right hand sides of Eq. (1). The normalized averaged stream wise velocityu/U∞is chosen as the target variable to gain the numerical and modeling error. The velocity and cavitation data are obtained from the medial surface along the span wise location.

Figure 1 shows the comparison of experimental and numerical snapshots of cavity shedding within one typical cycle. The experimental results are from Ref. [14]. Numerical results are used to represent the unsteady cavity evolution colored with vertical velocity. From Figs. 1(a)-1(d), it can be observed that the numerical results can capture the unsteady cavity evolution features, including the cavity inception,development and shedding along the hydrofoil suction face. The periodic cavity shedding behavior can lead to complex and turbulent flow structures. This can cause huge difficulties to accurately simulate the unsteady cavitating flow even with well performance numerical methods. Owing to the extensive use of LES in academic research in recent years, the reliability or risk assessment has become an essential step for LES results in cavitation. At present, it has the possibility to carry out quantitative LES errors analysis in cavitation simulation. Verification and validation of LES will be a necessary procedure in the future.

Fig.1 (Color online)Timeevolution of cavity shedding in one typical cycle for Case1 (Left: Experimental results[14].Right: Cavitation patterns by iso-surface of αv=0.1)

Figure 2 presents the average values versus different flow time about the normalized stream wise velocityu/U∞at monitoring point A (x/c=0.2,y/c=0.09) and point B (x/c=0.8,y/c=0.16). It can be seen that the variations ofu/U∞at the ending of statistical flow time are clearly smaller compared to the beginning of flow time. This ensures that the selection of final averaged velocity in this paper has almost no effect on obtaining the LES errors.

Fig.2 Average values versus different flow time about the normalized stream wise velocities at monitoring points

The magnitudes of numerical error and modeling error for Case 1 are shown in Fig.3 for the unsteady cavitating flow. From the results, it can be seen that the modeling error and numerical error are almost on the same order of magnitude in most situations, while the modeling error is often a bit larger if compared to numerical error. For each chord wise location in Fig.3,the numerical error and modeling error sometimes partially have opposite signs and they can offset each other. In Fig.3(a), the errors are large and squeezed in very little space at vertical direction, but sharply decrease to almost zero. The cavitation occurs generally around this narrow location, and the accuracy of the inner cavitating flow structure at this narrow location is a great difficulty for numerical simulation,also for experiments. This might be in charge of the error distribution in Fig.3(a). From Figs. 3(b)-3(e),the numerical and modeling errors start to oscillate along the vertical direction. The errors magnitudes and fluctuation levels gradually become larger fromx/c=0.4 tox/c=1.0. It has the similar tendency that the errors decrease to almost zero when the distance is far away from foil surface. The cavitation area becomes thicker from Figs. 3(b), 3(e). The velocity fluctuate sviolently due to the periodic cavity shedding,which can cause much large scale vortexstructure. It has a huge impact on the cavitation simulation. This might result in the errors changing in a large range. From above analyses, it can be con-cluded that the LES errors are significantly influenced by the unsteady cavitation.

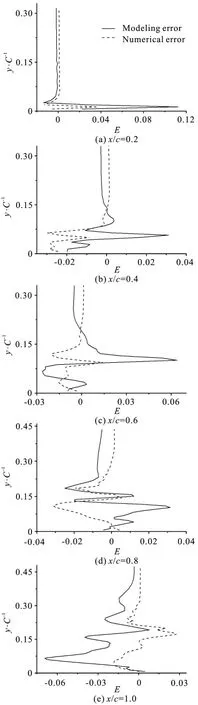
Fig.3 The numerical errors and modeling errors of averaged u/ U∞ at five chord wise locations for Case 1

Large eddy simulation and error analyses of the attached turbulent cavitating flow around the Clark-Y hydrofoil has been made in this letter. Quantitative LES errors analyses of cavitation simulation are carried out and cavitation influence on LES errors is also discussed. The main conclusions can be summarized as follows:

(1) The numerical results can capture the periodic cavity shedding behavior and they are in well agreement with the experiments. The shedding of cavity can lead to complex and turbulent flow structures,which results in great difficulties to model the details of the turbulent cavitating flow even with well performance numerical methods.

(2) In this simulation of the transient cavitating flow, the modeling error and numerical error are on the same order of magnitude in most situations, while the modeling error is often a little bit larger than numerical error. The numerical error and modeling error sometimes have the opposite sign and they can partially offset each other.

(3) The numerical error and modeling error are significantly influenced by the cavitation. The unsteady cavitation can extend the magnitudes and oscillation levels of LES numerical error and modeling error.

It still has a long way to go for the quantitative LES reliability estimation with V&V. Owing to the extensive use of LES in academic research in recent years, the LES reliability estimation should become an essential part to LES results in cavitation. Due to that Smagorinsky constant cannot change arbitrarily, the LES error estimation method adopted in this paper needs more investigations. The three-equation method proposed by Dutta and Xing[16]may give more promising results. The LES error estimation applied in the unsteady cavitation simulation with the guideline of Ref. [16] will be the focus of our future investigations.

[1] Li X. S., Li X. L. All-speed Roe scheme for the large eddy simulation of homogeneous decaying turbulence [J].International Journal of Computational Fluid Dynamics,2016, 30(1): 69-78.

[2] Li X. S., Xu J. Z., Gu C. W. Preconditioning method and engineering application of large eddy simulation [J].Science in ChinaSeries G-Physics, Mechanics and Astronomy, 2008, 51(6): 667-677.

[3] Wu Q., Huang B., Wang G. et al. The transient characteristics of cloud cavitating flow over a flexible hydrofoil[J].International Journal of Multiphase Flow, 2018, 99:162-173.

[4] Cui P., Zhang A. M., Wang S. et al. Ice breaking by a collapsing bubble [J].Journal of Fluid Mechanics, 2018,841: 287-309.

[5] Peng X. X., Ji B., Cao Y. et al. Combined experimental observation and numerical simulation of the cloud cavitation with U-type flow structures on hydrofoils [J].International Journal of Multiphase Flow, 2016, 79:10-22.

[6] Ji B., Luo X., Arndt R. E. A. et al. Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil [J].International Journal of Multiphase Flow, 2015, 68:121-134.

[7] Wang Y., Xu C., Wu X. et al. Ventilated cloud cavitating flow around a blunt body close to the free surface [J].Physical Review Fluids, 2017, 2(8): 084303.

[8] Long X., Cheng H., Ji B. et al. Large eddy simulation and Euler-Lagrangian coupling investigation of the transient cavitating turbulent flow around a twisted hydrofoil [J].International Journal of Multiphase Flow, 2018, 100:41-56.

[9] Cheng H. Y., Long X. P., Ji B. et al. 3-D Lagrangian based investigations of the time-dependent cloud cavitating flows around a Clark-Y hydrofoil with special emphasis on shedding process analysis [J].Journal of Hydrodynamics,2018, 30(1): 122-130.

[10] Long Y., Long X., Ji B. et al. Verification and validation of URANS simulations of the turbulent cavitating flow around the hydrofoil [J].Journal of Hydrodynamics, 2017,29(4): 610-620.

[11] Xing T. A general framework for verification and validation of large eddy simulations [J].Journal of Hydrodynamics, 2015, 27(2): 163-175.

[12] Freitag M., Klein M. An improved method to assess the quality of large eddy simulations in the context of implicit filtering [J].Journal of Turbulence, 2006, 7(40): 1-11.

[13] Dutta R., Xing T. Quantitative solution verification of large eddy simulation of channel flow [C].Proceedings of the 2nd Thermal and Fluid Engineering Conference and 4th International Workshop on Heat Transfer, Las Vegas,USA, 2017.

[14] Huang B., Young Y. L., Wang G. et al. Combined experimental and computational investigation of unsteady structure of sheet/cloud cavitation [J].Journal of Fluids Engineering, 2013, 135(7): 071301.

[15] Ji B., Long Y., Long X. P. et al. Large eddy simulation of turbulent attached cavitating flow with special emphasis on large scale structures of the hydrofoil wake and turbulence-cavitation interactions [J].Journalof Hydrodynamics,2017, 29(1): 27-39.

[16] Dutta R., Xing T. Five-equation and robust three-equation methods for solution verification of large eddy simulation[J].Journal of Hydrodynamics,2018, 30(1): 23-33.