从应用型人才培养谈《数字信号处理》的教学改革

2018-05-14张晓娟

山西电子技术 2018年2期

张晓娟

(太原工业学院电子工程系，山西太原 030008)

0 引言

2014年教育部提出了应用型人才的培养，相应的院校开始积极部署，朝着应用型方向转型发展，主要表现在压缩理论课程授课学时，增加实验、课程设计和各层次实践等环节学时。《数字信号处理》作为电子信息工程和通信工程等专业的核心课程，其特点表现在概念抽象、理论性强、数学推导复杂、可视化差[1]，即便课上用Matlab，Python等仿真工具进行仿真也很难使同学们对某个知识点一目了然。而且，如何使本课程的教学适应应用型人才的培养，如何使本课程的理论算法与实践相结合，如何更能激发学生的自主学习能力，如何培养学生分析问题和解决问题的实际能力是本次教学改革关注的方面。

1 生活实例引入

《信号与系统》课程中一个核心知识点：时域采样定理，也称奈奎斯特采样定律，简单用公式表述如式(1)所示，《数字信号处理》课程中另一个核心知识点：频域采样定理，如式(2)所示，同时为形象的展示该内容，会给出简图表示，如图1所示。若不满足抽样定理，如图1(h)，由于ωh较大，使得ωs<2ωh，则原始信号无法恢复，原因是时域抽样过程使频谱出现混叠。为进一步强化教学效果，在课堂上甚至加入了matlab仿真演示。

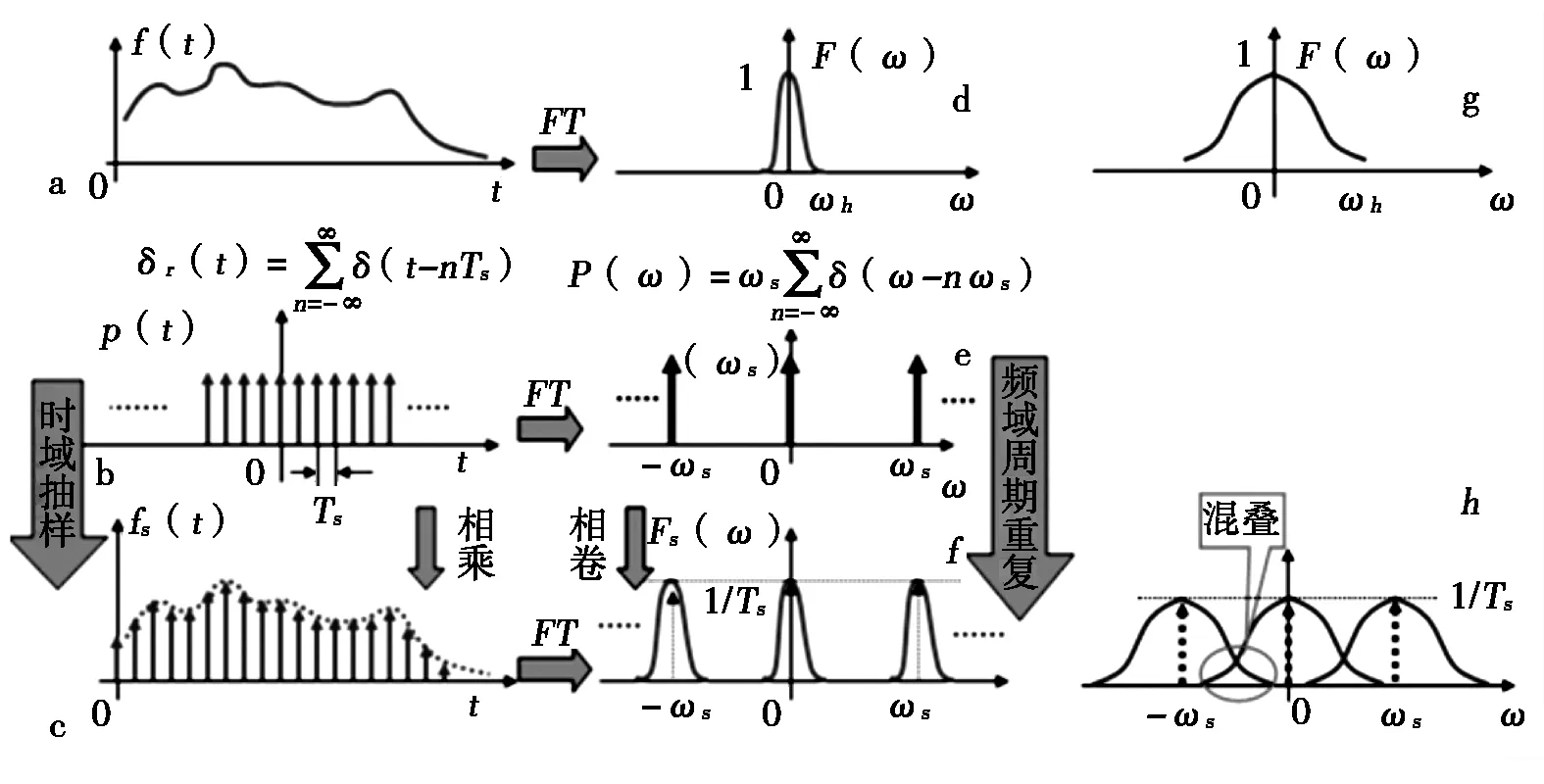
图1 时域抽样定理过程图

fs≥2fh.

(1)

其中，fs为抽样频率，fh为信号最高频率。

N≥M.

(2)

其中，N为频率采样点数，M为信号长度[2]。

结论同学们记住了，但不知道现实中如何用。此时如果举个与他们的生活息息相关的例子，问题则更容易理解。比如，以歌曲为例，提示同学们下载的歌曲大部分为mp3(Moving Picture Experts Group Audio Layer-3)格式，mp3格式本身就是把模拟信号转换为数字信号再进行压缩。假如录制一首歌曲(模拟信号)3分钟，通过抽样→量化→编码变为数字信号，若抽样过程只抽取128个点(对应低抽样频率)，自然听不到连续流畅的歌曲。那么如果抽4 096个点，抽16 384个，或者抽32 768个点(对应高抽样频率)，结果又会怎样？哪怕不理解这些知识，根据生活经验，同学们也知道抽的点数越多，听起来越连贯。但是问题又来了，如果抽16 384个点就能听到流畅的歌曲，那么抽32 768个点，单流畅度而言，肯定更好，但如此之多的点对之后的量化、编码操作时间是个考验，对存储空间也是考验。所以，抽样点数够用即可，反映到公式上即：fs≥2fh.

另外，频率抽样设计法的思想是在频域内，用有限个频率点抽样，近似所希望的理想频率响应Hd(ejω)。例如要设计一个截止频率ωc=0.4π的低通滤波器，抽样点数N=20，如图2所示[2]。由图2(a)图和(b)图可以看出，理想滤波器近似出来的实际滤波器有误差，正肩峰和负肩峰比较大，如何克服这个误差呢？增加过渡带点数，如图2(c)图所示，这样误差减小,如图2(d)图所示。这个道理实际生活中处处存在，高空坠物，如果中间被缓冲一下，砸下来的“坑”自然就变小了。

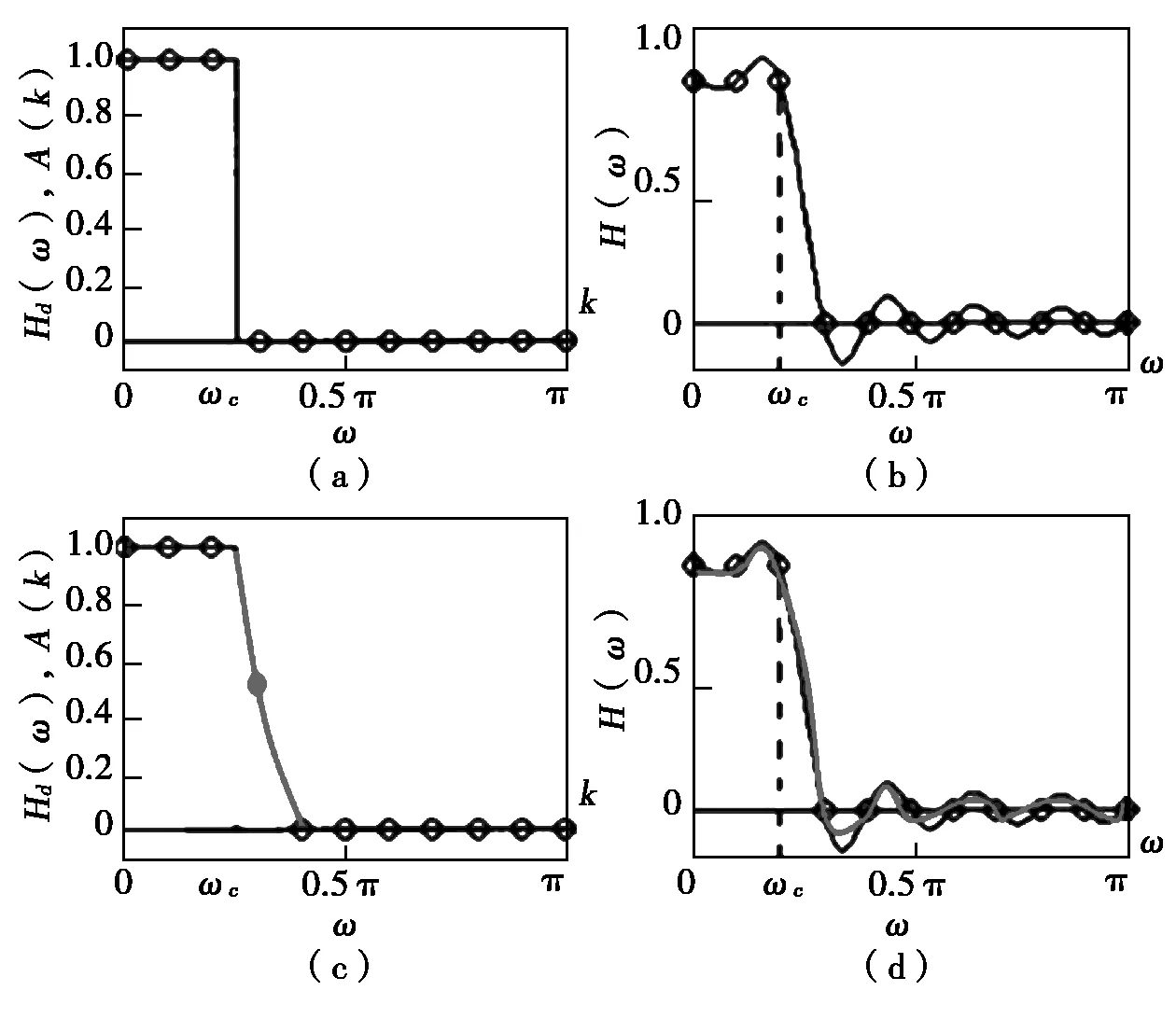
图2 频率采样设计法误差分析对比图

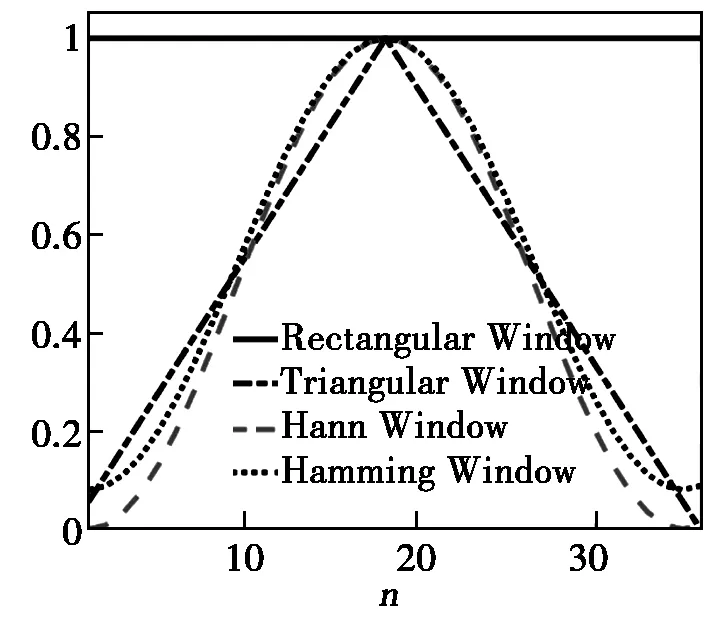
图3 几种窗函数时域波形图

再比如，如图3所示各种窗函数的比较，矩形窗(rectangular window)，三角窗(triangularwindow)，汉宁窗(Hanning window)，哈明窗(Hamming window)，布莱克曼窗(Blackman window)，这里只给出了窗函数的时域波形图，时域表达式未给出，因为这几个窗函数的时域表达式越来越复杂，不作为重点要求同学们记住，只要会根据指标选择窗函数即可。但从这几个窗函数的时域波形图可以看出，矩形窗是刚性的截断，三角窗是过渡的截断，其余三个窗函数是柔性的截断，性能自然会比矩形窗好一些，例如旁瓣峰值越来越小(重要指标)，相应的主瓣宽度略有增大。

从这些生活实例的引入可以看出，《数字信号处理》的知识点本身很抽象，但是“道法自然”，很多规律是相通的，用同学们经常见到的，耳熟能详的规律解释本课程的某些思想和算法，就能站在他们的角度帮助他们理解知识，应用知识。

应用型人才的培养，更是为我们提供了不少教学素材，比如数码相机的原理，同学们肯定非常感兴趣，可以介绍CCD成像原理让他们感受数字世界的奇妙。还有数字电视、数字音响等，都可以分析从模拟设备到数字化的过程。

2 “反转课堂”教学

为激发学生的自主学习兴趣在部分章节用了“反转课堂”教学。因为《数字信号处理》是《信号与系统》的后续课程，如果《信号与系统》掌握不好，本课程的学习就会有困难，而且本课程的概念比较抽象，数学推导复杂，如果整个授课过程都采用“反转课堂”教学效果并不理想，因此，只对部分章节用了“反转课堂”教学。

“反转课堂”教学的难点是如何设计“问题”，让同学们带着“问题”看书找答案，从而理解知识点。这些“问题”既不能太笼统，也不能太详细，还不能过于简单或复杂，而且要根据同学们的知识掌握程度来设计，在这些条件下设计“问题”考验着每位教师。经过我们教研组讨论，设计了如下问题：

1) 预习非周期序列的傅里叶变换的性质，注意其中的对称性质，理解它们相互之间的对应关系，如图4所示。

2) 复习X(Z)和X(ejω)的定义，预习X(k)，并找出三者之间的关系，如图5所示。

3) 复习线性卷积定理，预习循环卷积的定义和计算过程，计算x(n)={1,2,3,4}，h(n)={1,1,1,1}，求x(n)*h(n)，x(n)⑤h(n),x(n)⑥h(n),x(n)⑦h(n),x(n)⑧h(n)和x(n)⑨h(n)，并说明线性卷积和循环卷积的区别。得出结论：满足式3，循环卷积才不失真，此时循环卷积与线性卷积相等[2,3]。课上一定要强调混叠部分，这里的混叠比模拟信号更容易理解。

N≥M+L-1.

(3)

其中，N为循环卷积长度，M为信号x(n)的长度，L为信号h(n)的长度。

4) 复习DFT，并尝试计算16点DFT复数乘法次数和复数加法次数，思考如何能降低这些次数，预习FFT。

5) 在桂志国主编的《数字信号处理》第二版里前四章都在介绍信号及信号的变换，第五章开始讲系统，那么，在大家的印象里，系统是什么样子？类似于电路系统，这里主要讲述IIR和FIR滤波器的结构，预习IIR滤波器直接Ⅰ型、直接Ⅱ型、级联型和并联型的画法。

6) 请大家结合所学知识，用一个公式表达出低通滤波器的幅频特性曲线，如果表达不出，请大家参考巴特沃斯和切比雪夫给出的模拟低通滤波器的幅度平方函数，用描点法检验函数是否为低通滤波器。

7) 巴特沃斯和切比雪夫给出了模拟低通滤波器的幅度平方函数，如何将幅度平方函数变换成数字滤波器的系统函数？

8) 在理解数字低通滤波器设计方法的基础上，预习数字高通滤波器、带通滤波器和带阻滤波器如何设计。

图4 时域与频域的对称关系图

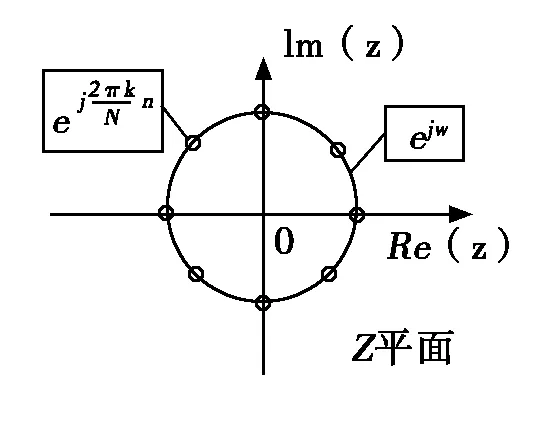
图5 X(Z)、X(ejω)和X(k)关系图

9) 预习窗函数设计法的思想，设计数字低通滤波器和数字高通滤波器。

10) 预习频率采样设计法设计低通滤波器。

通过这些问题的设计，让同学们带着问题提前预习，并且会在课堂上随机抽查他们预习的效果，这样不仅可以激发他们自主学习的能力，而且可以丰富课堂教学形式，关键是学生们很热爱这种互动的教学方法，经过一学期5个班的实验，这种教学方法收效甚好。

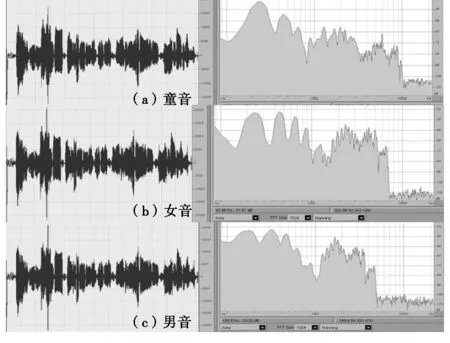
图6 三种不同的语音信号时域与频域分析图

3 形象化教学

课堂对学生来说就是视听觉的冲击，在短时间内接受并理解一个甚至多个知识点，对他们的压力颇大，如果在视觉上或听觉上，更好的是视觉听觉同时给予他们喜爱的刺激，效果会更好。

在本课程的教学中，用Matlab把关键知识点进行仿真，通过修改参数使同学们理解该参数的意义和重要性是比较流行的授课方法[4]。本教研室也把这种方法列为常规的教学方法，更有特色的是，我们还利用Cool Eidt Pro 2.1音频仿真软件来增加同学们的视听效果，通常现场采集同学们的语音，然后进行离散化，频谱变换和分析[5]。如图6(b)左为采集的某女生的语音，右为傅里叶变换得到的幅频特性图，从图中可以看出，该女生的频域范围约为0～7 kHz。图6(a)的左半部分还是原始录音，不同的右半部分的低频部分被削弱，高频部分被增强，频带被展宽，频率范围约为0～10 kHz，结果播放的语音变为童声。图6(c)左半部分依然为原始录音，右半部分的低频部分被增强，高频部分被削弱，同时频带变窄，约为0～5 kHz，结果播放的语音变成了男声。

实验结果与同学们的认知非常一致，小孩声音脆，因为频率高，女声较男声甜就是因为女声频率高于男声，越老成的声音频率越低。通过这种视听觉的冲击，绝大部分学生理解了频谱变换和频谱分析的重要性，再也不会怀疑记住傅里叶变换公式到底有用没用。