非结构网格上可压缩Euler方程的并行算法

马欣荣，史瑞琪

（咸阳师范学院 数学与信息科学学院，陕西 咸阳 712000）

非结构网格具有优越的几何灵活性和普适性，对复杂区域边界和约束情形有很强的适应性，克服了结构网格（直交网格）不能适应在任意形状和任意区域进行剖分的缺陷，更容易处理复杂几何外形。基于非结构网格的算法不断发展，但往往存在存储量较大和计算量大等缺点，存储格式中需要存储节点坐标以及标识单元间的相邻接的关系，直接影响了这类算法的计算效率。为了提高计算效率，各种高效的数值计算方法不断发展，尤其是适合于线性和非线性系统方程的求解、不受控制方程时间和空间离散格式的限制，并且满足最优渐进的性质的多重网格方法[1-5]。

随着计算机技术和数值分析方法的发展，工程中大型计算问题需要成千上万亿次级的运算能力，串行算法已经不能满足计算需求，所以集群计算成了当前科学计算的必要途径之一。区域分解算法便是其中有效的求解方法之一，它具有诸多优点：缩小计算规模；使用熟知的算法；无需采用整体一致网格，甚至子区域间可以使用不同的离散方法；子区域可以选用不同的数学模型；算法高度并行。由此在CFD应用中得到了研究工作者的青睐。朱国林等[6]人主要研究了分布式并行处理系统的搭建与实施以及CFD计算程序的并行化，提出了并行化的关键是隐式算法中边界上各类通量的信息传递的正确性。Hauser等[7]提出了求解Navier-Stokes方程直接数值模拟并行算法，降低了大型问题的海量计算成本。文献[8]提出了三维Euler方程的三分区、四分区网格上的并行算法，负载平衡较好时能够保持较高的并行效率。文献[9]基于MPI中的染色分层通信技术，适当处理块边界通信问题，采用隐式时间离散算法进一步提高计算效率，求解了三维黏性流场。赵伟波等[10]在非结构网格上设计了层次化的网格数据结构实现了并行有限元方法，并应用于弹性力学方程组的求解。

本文在文献[11]基础上，最大限度保证数据信息传递最少，各处理器保持负载均衡。采用LU-SGS隐式时间离散技术提高推进效率，结合最大当地时间步长技术以及V循环-多重网格方法求解欧拉方程组，数值计算结果表明了本文算法的可行性，适合在集群系统下进行像群计算。

1 数值离散算法

1.1流动方程

在笛卡儿坐标系下的非定常欧拉方程守恒形式：

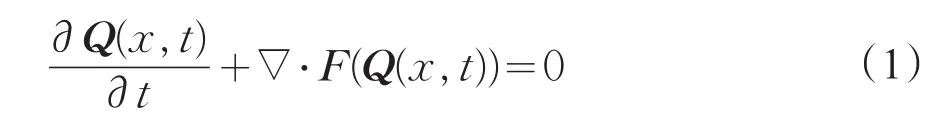
其中Q、F分别为守恒变量和通量，定义如下：

其中ρ,e,p分别为密度、单位体积总内能和压强，ui为速度各方向的分量，δij为克罗内克尔符号。考虑理想气体的热力学特性：

其中γ为比热比，空气取为γ=1.4。

1.2流动方程离散方法

采用

有限体积方法可得

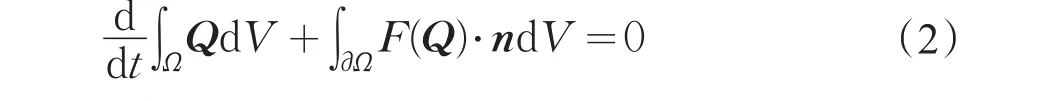
在控制体i上对方程(2)进行离散得到

式（3）为关于时间方向的一阶常微分半离散方程组。相对于显式时间离散格式而言，隐式时间离散格式可以放宽稳定性条件，所以本文采用LU-SGS隐式时间离散格式。

运用Euler向后差分离散以及线化处理后可以得到

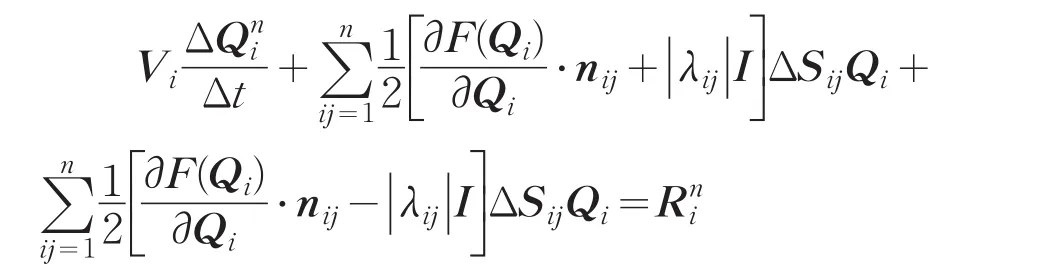
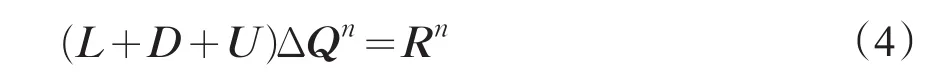
其中L为严格下三角矩阵，D为纯对角矩阵，U为严格上三角矩阵。

将式(4)变形并略去高阶小量可以得到

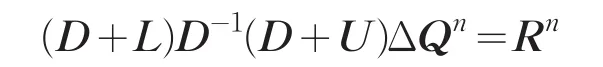
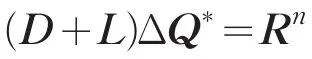
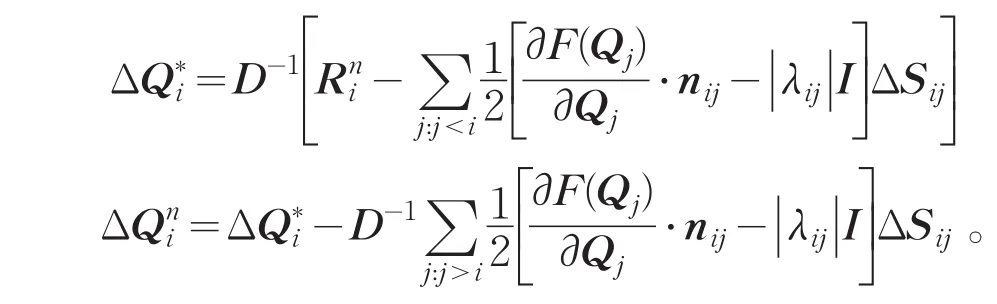
在实际计算过程中，为了提高计算效率，本文采用了SOR内迭代预处理技术。采用Roe[12]格式处理通量函数，限制器采用Venkatakrishnan[13]限制器。

2并行实现

2.1网格划分

采用多级图分区方法划分网格，保证各子区域交界面数量最少且网格独立保存，仅在相邻子区域间数据传递，实现同步计算，较好地减少通信等待时间以提高计算效率。边界分为物面边界、远场边界和分区内边界。物面满足无穿透条件，远场满足无反射条件。人工边界引入虚拟单元进行数据传递，见图1。

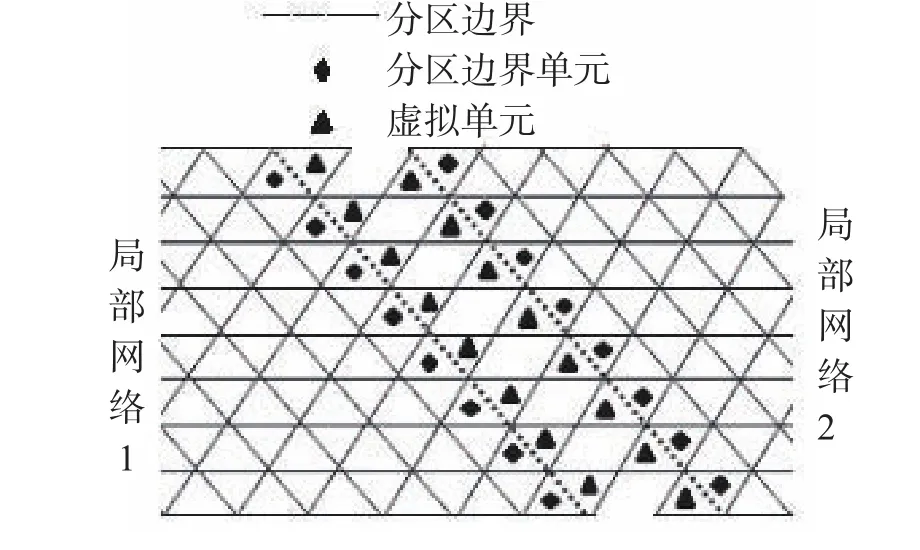
图1子分区边界

2.2数据传递

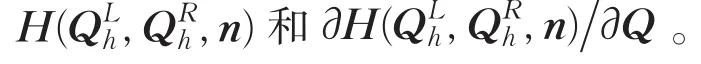
3 数值实验

3.1绕NACA0012翼型跨音速无黏流动

计算状态：来流马赫数 Ma=0.8，攻角α=1.25°，收敛误差为ε=10-10。图2给出了八分区网格，网格单元共10 216个，网格节点共5 233个。包括虚拟单元的子区域单元网格数为：1 360、1 366、1 317、1 319、1 389、1 364、1 308、1 422。图3给出了单个处理器、多处理器以及翼型实验值的压力系数对比，可以看出数值计算结果与实验值吻合。实验数据见表1，可以看出本文算法10台处理器并行效率保持在70%以上，优于文献[11]的计算结果。此外，随着网格数量的增加，并行效率会随之增加，基本呈线性变化。与参考文献[14]相比较，单处理器与多处理器计算结果显示物面压力系数分布和激波位置与其保持一致。

图2 NACA0012翼型八分区网格

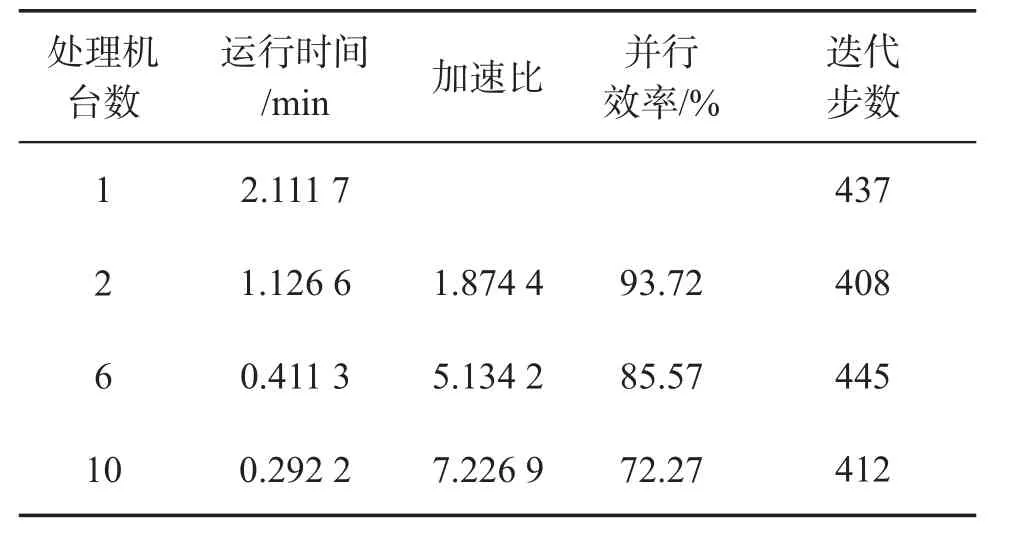
表1 NACA0012翼型数值模拟并行性能

3.2 DLR-F6跨音速绕流

来流马赫数：Ma=0.75，攻角：α=0∘，图4给出了四分区全局网格，网格单元共有1 453 849个，网格节点共275 561个。图5给出了F6翼身组合体物体表面等密度线。单处理器计算99 100步需要152.056 9 min，10台处理器计算需要27.080 1 min，并行效率为70.92%，优于文献[11]的计算结果，残值下降12个量级。表2给出了具体计算数据，每迭代100步输出一次计算结果。同样通过数值实验能够验证随着网格量的增加，并行效率会随之增加，基本呈线性变化。

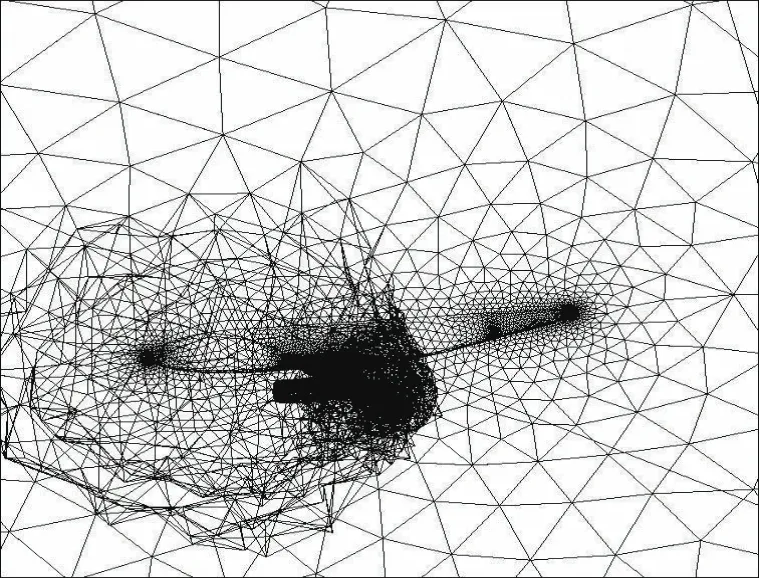
图4 DLR-F6四分区网格

图5 DLR-F6翼身组合体等密度线

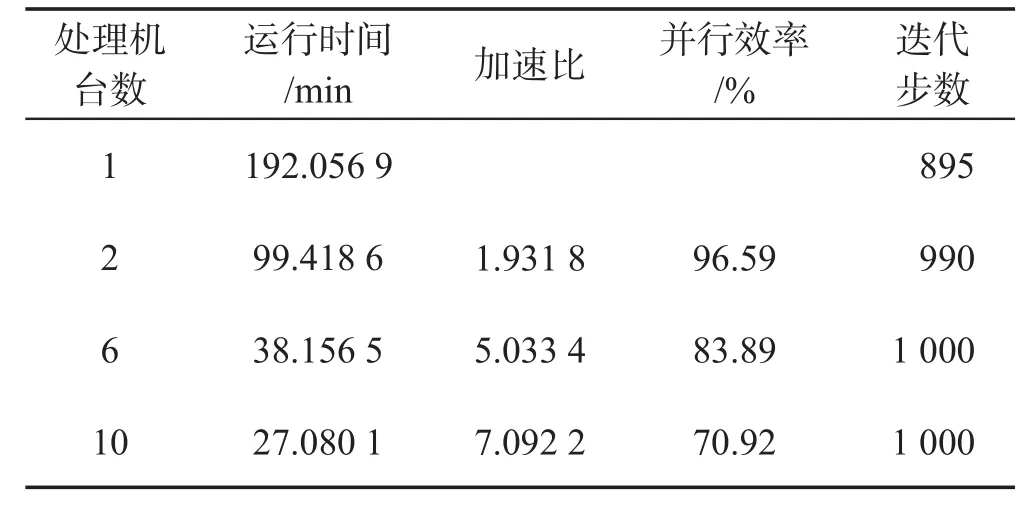
表2 DLR-F6翼身组合体数值模拟并行性能

4结论

本文并行计算了双曲守恒率，构造虚拟单元，仅在相邻处理机间进行数据通信，使算法具有较好的并行性。结合当地时间步长、隐式LU-SGS时间离散方法以及多重网格技术加速收敛，在实际计算中，LU-SGS算法采用了预处理技术，相对于GMRES隐式格式计算效率相当，而且能进一步减小存储要求，格式构造简单、易于编程实现，10台处理器并行效率优于文献[11]的计算结果，保持在70%以上。为进一步求解复杂外形黏性流场提供了依据。

参考文献：

[1]SOLCHENBACH K,TROTTENBERG U.On the multigrid acceleration approach in computational fluid dynamics[C]//Proc of the 4thInt’l DFVLRSeminar on Foundations of Engineering Sciences：Parallel Computing in Science and Engineering.Bonn：Springer-Verlag，1988：145-158.

[2]YANG UM.Parallel algebraic multigrid methods-High performance preconditioners[C]//Proc of the Numerical Solution of Partial Differential Equations on Parallel Computers.Heidelberg，Berlin：Springer-Verlag，2006：209-236.

[3]HULSEMANN F，KOWARSCHIK M，MOHR M，et al.Parallel geometric multigrid[C]//Proc of the Numerical Solution of Partial Differential Equations on Parallel Computers.Heidelberg，Berlin：Springer-Verlag,2005：165-208.

[4]李宗哲.非结构网格的并行多重网格算法研究[D].长沙：国防科技大学，2012.

[5]刘冰，陆中华，李新亮，等.基于GPU的多重网格Navier-Stokes解算器并行优化算法研究[J].科研信息化技术与应用，2013，4（3）：56-67.

[6]朱国林，徐庆新.计算流体力学并行计算技术研究综述[J].空气动力学学报，2002，20（S1）：1-6.

[7]HAUSER T，MATTOX T I，LEBEAU R P，et al.High-cost CFD on a low-cost cluster[C]//Proceedings of the 2000 ACM/IEEEConference on Supercomputing,Computer Society.New York：IEEE,2000：55-91.

[8]兰黔章，吕晓斌.三维Euler方程的分区和并行计算[J].力学季刊，2001，22（4）：433-438.

[9]郑冠男，邓守春，韩同来，等.基于混合网格Navier-Stokes方程的并行隐式计算方法研究[J].应用力学学报，2011，28（3）：211-219.

[10]赵伟波，刘青凯，杨扬.非结构网格上弹性力学数值模拟的并行实现[J].计算机研究与发展，2015，52（5）：1153-1159.

[11]马欣荣,刘三阳.非结构网格上双曲守恒率的并行算法研究[J].四川大学学报（工程科学版），2015，47（2）：123-128.

[12]ROE P L.Approximate Riemann solvers,parameter vectors，and difference schemes[J].Journal of Computational Physics，1981，43（2）：357-372.

[13]VENKATAKRISHNAN V.On the accuracy of limiters and convergence to steady state solutions[R].AIAA Paper 93-0880，1993.

[14]BARTH T J，JESPERSEN D C.The design and application of upwind schemes on unstructured meshes[C]//27thAerospace Sciences Meeting,January 9-12，Reno，Nevada：AIAA Paper 89-0366，1989：1-12.